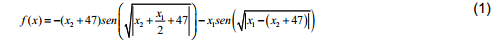INTRODUCCIÓN
La optimización es un tema muy estudiado en años recientes debido al continuo desarrollo de las herramientas computacionales y la necesidad de optimizar procesos en aras de utilizar los recursos de una manera más eficiente.
Existen una gran cantidad de métodos de optimización, los cuales se pueden agrupar en dos grandes grupos: clásicos y heurísticos. Para funciones objetivo complejas, con discontinuidades o poca concavidad-convexidad, los métodos clásicos quedan inhabilitados, por lo que se debe recurrir a las heurísticas. Uno de los métodos heurísticos más utilizados y estudiados, debido a su versatilidad, son los Algoritmos Genéticos (GA), una estrategia evolutiva que como casi todos los métodos, presenta una serie de parámetros que regulan su funcionamiento.
Los casos dónde la función objetivo suele ser muy compleja, como en la optimización estructural (ingeniería civil o mecánica), suponen una dificultad a la hora de encontrar una metodología capaz de enfrentar el problema con resultados satisfactorios. Se pudiera dar el caso de seleccionar un método de optimización apropiado para enfrentar el problema. Sin embargo, una mala selección de sus parámetros pudiera derivar en una falta de solidez de los resultados (ver Figura 1) (Smith y Eiben, 2010), perdiendo el proceso toda su esencia. Para enfrentar esta situación, hay una estrategia denominada ajuste de parámetros (parameter tuning en inglés), la cual no es más que una metodología propuesta para seleccionar una configuración conveniente del método ante un determinado problema.
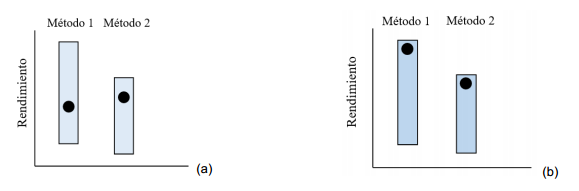
Fig. 1 Representación gráfica del beneficio del ajuste de parámetros; (a) métodos con parámetros sin ajustar, se puede apreciar como el método 1, aun siendo más apropiado para enfrentar el problema, presenta un rendimiento inferior que el número 2; (b) con el ajuste de parámetros se puede llegar a una configuración óptima, o cercana a esta, que permita un buen rendimiento (Smith y Eiben, 2010).
Resulta frecuente encontrar en la literatura el uso de métodos heurísticos para resolver problemas de optimización. No obstante, en muchos de estos casos no se hace referencia a la configuración del método utilizada, y mucho menos a algún indicio de ajuste de sus parámetros. Es cierto que este proceso suele ser tedioso y difícil de implementar. Por eso, otra alternativa pudiera ser buscar referencias de trabajos similares, y aplicar las mismas configuraciones utilizadas. Este trabajo tiene como objetivo principal,
brindar la mejor configuración de GA ante problemas de optimización de elevada complejidad, con funciones objetivos difíciles de optimizar.
Como se había mencionado, algunos procesos de optimización pueden ser extremadamente costos, especialmente los relacionados con optimización estructural (Negrin, y otros, 2019a; Negrin, y otros, 2019b), por lo que el ajuste de parámetros resulta casi imposible de realizar. Para solucionar este problema, existen varias funciones, denominadas “de referencia” (Suganthan, y otros, 2005; Smith y Eiben, 2010), las cuales varían en cuanto a complejidad. Lo que se propone es utilizar una de estas, con características similares al problema real, como función de estudio en el ajuste de parámetros (ver Figura 2). La configuración obtenida es la que se utilizaría en la resolución del problema real. En este estudio se utiliza la función Eggholder, de elevada complejidad, con muchos óptimos locales, para ajustar los parámetros de GA. Esto significa que, ante la necesidad de enfrentar un problema complejo de optimización, que genere superficies de respuesta igualmente complejas, difíciles de optimizar, las recomendaciones brindadas en este estudio pudieran ser utilizadas.
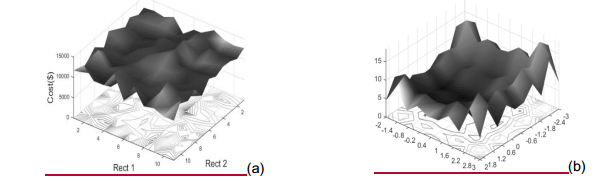
Fig. 2 Uso de funciones de referencia para simular problemas reales, (a) superficie de respuesta de caso de optimización estructural, rectangularidad de cimentaciones superficiales para este caso, (b) uso de función Ackley para simular caso real
Aun adoptando una buena configuración del método, se pudiera dar el caso que este, en su forma simple, fuera incapaz de brindar resultados consistentes. Ante esta situación se pueden adoptar otras estrategias. En este artículo, se propone como otra alternativa, utilizar la optimización con variables enteras en vez de
continuas. Aun así, los resultados pueden ser mejorables, por lo que se propone un método compuesto basado en la generación de una población inicial, utilizando el propio GA simple.
El artículo se estructura de la siguiente manera. En la sección de materiales y métodos, se brindan algunos resultados obtenidos por otros autores en estudios similares, se introducen las características fundamentales de la función de estudio, se hace una breve explicación de las características principales de los GA, se explica el proceso de ajuste de parámetros y se desarrolla la idea de la nueva metodología propuesta. Finalmente se muestran los resultados del ajuste de parámetros, del uso de variables enteras y de la aplicación del método compuesto, con la correspondiente discusión y conclusiones.
MATERIALES Y MÉTODOS
Revisión bibliográfica
Varios trabajos se han enfocado en el estudio los parámetros de funcionamiento de los GA. En (Roeva, y otros 2013) se optimiza una función de tres variables y se obtiene que el tamaño de población óptimo es de 100 individuos. Al aumentar este valor, los resultados no mejoran, con un aumento considerable del tiempo computacional.
Llevando a cabo un experimento utilizando un 50% de elitismo, un punto de cruzamiento y un 1% de mutación, se concluye que: para tamaños de población arbitrariamente grandes, la precisión del algoritmo genético aumenta, pero no alcanza el 100%. Cuanto mayor es el tamaño de la población, mayor es la probabilidad de que el estado inicial de la población contenga un cromosoma que represente la solución óptima (Gotshall, y otros, 1992).
Después de estudiar varios trabajos, se pudo concluir que no hay duda de que el escalado de la función de aptitud juega un papel esencial en la optimización mediante algoritmos genéticos. Los GA son muy adecuados para tareas de optimización, especialmente cuando las funciones de ajuste o escalado (objetivo) son bastante complicadas (Sangeeta, 2016). Con la optimización de cuatro funciones para obtener los mejores escalados de la función aptitud, los resultados obtenidos indicaron claramente que el escalado tiene un efecto dramático en la diversidad genética y en la tasa de convergencia. En este caso, el escalado lineal aumenta la diversidad y depende de la función; si se estuviera puramente interesado en encontrar una solución rápidamente, entonces se debería usar escalamiento exponencial; el escalamiento tipo rank fue el único otro método para seleccionar como el máximo de la primera función de prueba, y lo hace con una precisión de 5 dígitos. Pero, si la función de aptitud (objetivo) fuera más complicada que cualquiera de las probadas, donde hubiera múltiples picos y se necesitara preservar la diversidad genética durante muchas generaciones para explorar todos estos picos, la escala top parece ser la mejor opción (Sadjadi, 2004).
Sobre los métodos de selección, se puede decir que para que la evolución tenga lugar, la etapa de reproducción debe tener los mejores individuos. Por lo tanto, es necesario seleccionar a los individuos “mejores adaptados”. Dependiendo del tipo de aplicación, se debe usar el método de selección apropiado (Saini, 2017).
Al aplicar los GA al problema del vendedor viajero (travelling salesman en inglés) con un tamaño de población de 100 individuos, una fracción de cruzamiento y mutación del 70 y el 0.2 % respectivamente, y analizando tres métodos de selección: ruleta, torneo y elitismo, se concluye que el análisis comparativo de los resultados muestra claramente que el método de elitismo generó poblaciones más ajustadas en comparación con los otros métodos (Chudasam, y otros, 2011).
Comparando diferentes tipos de operadores genéticos y monitoreando su desempeño aplicado a un Sistema de Detección de Intrusos, para determinar el tipo de selección y cruzamiento que funcionen mejor trabajando en conjunto, se llega a la conclusión que las mejores opciones de selección aplicables a su estudio son elitismo y estocástica uniforme, con el cruzamiento uniforme (Firas, y otros, 2012).
En (Dillen, y otros 2018) se realiza el ajuste de parámetros de GA en la optimización del diseño de una estructura de acero de 25 barras, utilizando el peso de esta como función objetivo. La mejor configuración resultó ser un tamaño de población de 500 individuos, establecer un elitismo del 10 %, una fracción de cruzamiento de 0.80, utilizar el cruzamiento heurístico y la selección mediante tournament.
Se puede decir entonces que, para cada tipo de problema a resolver, se tienen en cuenta aspectos y se obtienen resultados diferentes. La elección de los valores de cada parámetro está en dependencia de las características de la función objetivo que se genere (cantidad de variables y complejidad de estas, tipo de restricciones, superficie de respuesta, etc.), por lo que, para alcanzar los resultados más satisfactorios posibles, resulta indispensable realizar un correcto estudio previo del problema en cuestión.
Función a optimizar
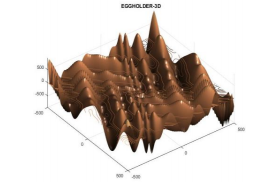
Uno de los objetivos fundamentales de este estudio es investigar el funcionamiento de los GA en determinadas funciones, para su posterior aplicación en problemas reales que presenten funciones objetivo con características similares a la utilizada. En este caso utilizaremos la función Eggholder, la cual presenta características particulares como la presencia de muchos óptimos locales, lo cual inhabilita el funcionamiento de una gran cantidad de métodos de optimización (Figura 3). Su formulación matemática se muestra en la ecuación 1.
Evidentemente es una función de una gran complejidad matemática, la cual, para el intervalo analizado (-500≤x≤500, -500≤y≤500), el óptimo global se encuentra en [482,06 432,58], con un valor de -956,92.
Algoritmos Genéticos
Los GA son una herramienta muy utilizada en la resolución de problemas de optimización. Están basados en la selección natural, una analogía con el proceso que gobierna la evolución biológica. Los GA modifican sistemáticamente una población de individuos (soluciones). En cada paso el algoritmo selecciona algunos individuos para que se conviertan en “padres” y generen los “hijos” de la siguiente generación.
El algoritmo se inicia con la creación de una población inicial de individuos (normalmente de un modo aleatorio, pero podrían usarse métodos determinísticos). El método compuesto de este estudio plantea generar una población inicial utilizando el propio GA simple.
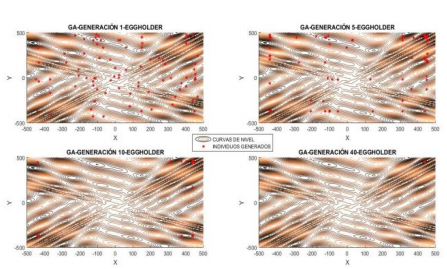
Posteriormente se asigna una aptitud a cada uno de los elementos de la población dependiendo de su valor en la función objetivo y del grado de cumplimiento de las restricciones del problema. Seguidamente, individuos de esta población son seleccionados de acuerdo con ciertas reglas (operador “selección”) y combinados entre sí (operador “cruzamiento”) para crear una nueva población. Finalmente, se emplean los operadores “mutación” para introducir nuevas características en la población (Paya, 2007). Con el paso de las generaciones, los individuos se van encerrando (o convergiendo) en las zonas de mejores soluciones, como se puede apreciar en la Figura 4.
En este trabajo se estudian los parámetros relacionados con el tamaño de población, la selección de los individuos y la reproducción (fracción y función de cruzamiento, elitismo) de estos para generar las nuevas poblaciones.
Ajuste de parámetros
Es ampliamente reconocido que el ajuste de parámetros puede mejorar significativamente el funcionamiento de un método ante un determinado problema (Eiben y Jelasity, 2002; Smit y Eiben, 2010; Huang, y otros, 2019). De acuerdo con (Smith y Eiben, 2011), los métodos para realizar el ajuste se pueden dividir en cuatro grupos: métodos de muestreo, basados en modelos, métodos de cribado y algoritmos meta-evolutivos. En este estudio utilizaremos una combinación de muestreo y cribado, mediante el uso de la curva de rendimiento promedio, introducida en el siguiente epígrafe.
Definiendo la utilidad
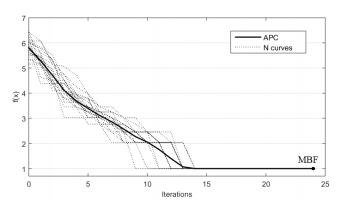
El concepto de utilidad en el ajuste de parámetros está relacionado con la medida que nos expresa la calidad del rendimiento de un método de optimización. Según (Eiben y Smit 2011), existen tres utilidades clásicas: mejor aptitud promedio (MBF por sus siglas en inglés), número de evaluaciones promedio para alcanzar la solución (AES por sus siglas en inglés) y tasa de éxito (SR por sus siglas en inglés). Todas estas pueden ser fácilmente extraíbles de la curva de rendimiento promedio (CRP) (ver Figura 5). En este estudio se utiliza como utilidad el MBF, además de la propia curva de rendimiento para comparar la efectividad de cada configuración a través de todo el proceso.
Metodología general para realizar el ajuste
La metodología consiste, de forma general, en fijar cada valor de cada parámetro analizado, mientras que los otros parámetros adquieren valores aleatorios. Para cada valor fijado se realizarán 2000 pruebas, para contrarrestar el carácter estocástico propio de las heurísticas y la aleatoriedad de los valores tomados por los otros parámetros. Al establecer un gran número de pruebas, aumenta la probabilidad de repetir cada posible combinación de valores de cada parámetro varias veces. El problema es el gasto computacional, por lo que es necesario encontrar un balance. La CRP reflejará el rendimiento del valor del parámetro fijado en todas estas pruebas.
En este caso, como se ha mencionado, se van a ajustar cinco parámetros. Tres de estos tomarán valores cuantitativos (PopSize, EliteCountFraction y CrossoverFraction) y los otros dos tomarán valores categóricos (SelectionFunction y CrossoverFunction). El tamaño de población (PopSize) podrá tomar los siguientes valores: 50, 100, 200, 300, 500, 800 y 1000. El parámetro asociado con el elitismo (EliteCountFraction) podrá ser 1, 5, 10 y 15 % del tamaño de población. La fracción de cruzamiento (CrossoverFraction) será 0.6, 0.8, 0.9 y 1.0. La selección se realizará por los siguientes métodos: stochastic uniform, remainder, uniform, roulette y tournament. El cruzamiento podrá ser scattered, intermediate, heuristic, single point, two points y arithmetic. En total se van a fijar 23 valores, y para cada uno, como se ha mencionado, se realizarán 2000 pruebas, lo que da un total de 46 000 procesos de optimización. Es por eso que este procedimiento resulta tan costoso. Si se tiene en cuenta que en trabajos de optimización estructural, un solo proceso de optimización puede tomar hasta 24 horas, la dificultad que sería ajustar los parámetros en el proceso real es evidente.
Para cada valor fijado, se obtendrán 2000 curvas de rendimiento, pertenecientes a cada una de las 2000 pruebas realizadas. De estas curvas se obtendrá la CRP de cada valor de cada parámetro. Cada una de estas curvas, pertenecientes a los cinco parámetros, será analizada de forma gráfica, además del correspondiente valor MBF.
El primer parámetro a ajustar será el tamaño de población. Una vez ajustado, este se fijará para las siguientes pruebas con los otros parámetros. Esto se hace con el objetivo de obtener CRP de características similares, ya que cada proceso de optimización tendrá los mismos conteos de función (cada vez que se evalúa un juego de valores de los parámetros en la función objetivo).
Método compuesto a partir de GA simple
En la sección de los resultados se puede comprobar que, el GA simple, aun con una buena configuración implementada, es incapaz de encontrar el óptimo global de manera regular para una función de la complejidad de la analizada.
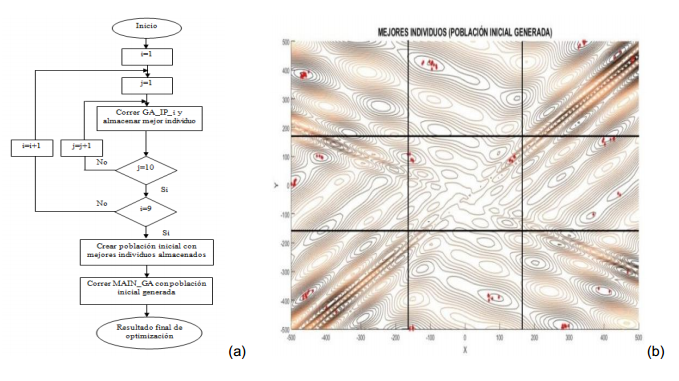
Para darle solución a esto, es necesario establecer una búsqueda más exhaustiva y eficaz por el espacio de soluciones. Esto se pudiera lograr creando una buena población inicial para el algoritmo simple, con individuos (o soluciones) de calidad. Estos métodos basados en poblaciones crean, generalmente, la primera población utilizando métodos aleatorios. Esto puede generar soluciones de poca calidad. Poblaciones iniciales de mejor calidad, deben garantizar una convergencia más rápida hacia mejores soluciones. Para asegurar esto, se propone realizar una búsqueda preliminar por el espacio de soluciones, almacenando las mejores encontradas. Una manera eficiente de explorar este espacio de soluciones es dividiéndolo en sub-espacios. Para este caso de dos variables se propone dividir cada variable en tres intervalos (ver Figura 6b), o sea, que se van a obtener nueve sub-espacios. Se realizará una búsqueda en cada uno de ellos para obtener los mejores individuos de cada sub-espacio, los cuales conformarán la población inicial para el algoritmo principal que, a partir de esta, recorrerá todo el espacio en búsqueda de la mejor solución global. Para cada una de las sub-poblaciones se correrá un algoritmo especial con uso de variables enteras, una sola generación y con una población de 100 individuos. Este proceso de repetirá 10 veces para cada sub-espacio almacenando el mejor individuo obtenido por generación, lo cual creará una población inicial de 90 individuos (10 por sub-espacio) con los mejores individuos de cada sub-espacio.
Esta población inicial será brindada finalmente al GA simple, con un tamaño de población de 200 y los parámetros ajustados, el cual se encargará de realizar la optimización en todo el dominio.
En la figura 6a se muestra un diagrama con el funcionamiento básico del algoritmo propuesto donde GA_IP_i representan los nueve archivos (GA_IP_1, GA_IP_2,…, GA_IP_9) que se encargarán de realizar las búsquedas locales en los sub-espacios de la función, donde i=1:9. MAIN_GA es el archivo con la sintaxis de GA simple y las correspondientes opciones de funcionamiento, incluyendo la población inicial generada con anterioridad.
Resultados y discusión
Ajuste de parámetros
Como se ha mencionado con anterioridad, en este epígrafe se mostrarán los resultados del proceso de ajuste de parámetros. Para esto se mostrarán los resultados de las 2000 pruebas para cada configuración, de donde se obtendrá la CRP y el valor MBF, obtenido de la propia curva.
Opciones de población
Es evidente que el tamaño de población es un parámetro extremadamente influyente en el funcionamiento de cualquier estrategia evolutiva. Tamaños de población pequeños resultan en una convergencia más rápida del algoritmo, aunque esto significa una búsqueda menos exhaustiva por el espacio de soluciones, aumentándose la posibilidad de quedar encerrado en un óptimo local. Tamaño de poblaciones grandes aseguran un mejor recorrido, pero se aumenta el tiempo computacional.
Un elemento principal a tener en cuenta es el número de variables. La función analizada presenta solamente dos, pero se puede apreciar que la superficie de respuesta es extremadamente compleja. La presencia de muchos óptimos locales, ubicados sin ningún tipo de orden, o sea que no siguen ningún patrón determinado, hace que la búsqueda se complejice a sobremanera.
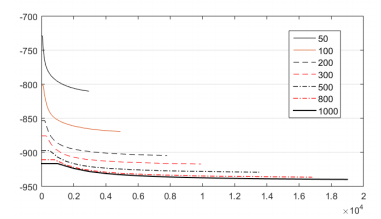
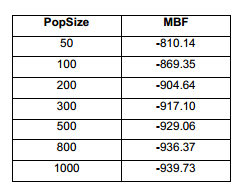
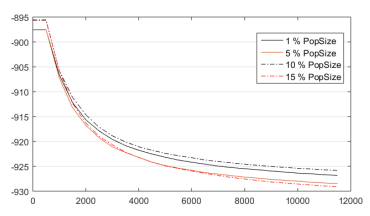
En la Tabla 1 y la Figura 7 queda demostrado que, con poblaciones pequeñas, menores de 200, los resultados son muy pobres. Los mejores se obtienen para una población de 1000 individuos. Es evidente que, al aumentar el tamaño de población, la búsqueda es más exhaustiva. La desventaja es el costo computacional. En secciones previas se argumentó cuan costosos algunos procesos de optimización pueden ser. Por tanto, es necesario encontrar un balance entre los dos objetivos, es decir, lograr buenos resultados con una convergencia razonablemente rápida. En función de esto, se establecerá como tamaño de población idóneo el de 500, y se continuará trabajando con este.
Opciones de selección
Estas opciones están relacionadas con la selección de los padres para la nueva generación. En las estrategias evolutivas, la selección de los padres para producir hijos es extremadamente importante. Es de suponer que la selección de los mejores individuos (más adaptados, con mejor valor de aptitud) deriva en la mejor obtención de hijos. Pero no siempre es así, y, al igual que las mutaciones, el cruzamiento entre un individuo bien adaptado con uno que no lo esté tanto, puede derivar en un individuo o solución de gran calidad.
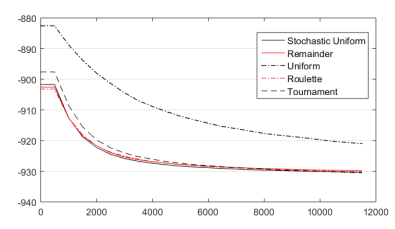
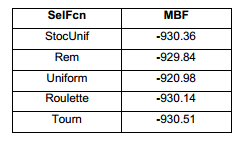
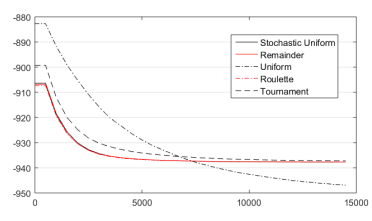
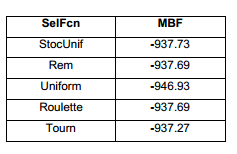
En la Figura 8 y la Tabla 2 se puede apreciar que hay cuatro funciones con resultados muy similares. Esto significa, que, independientemente de los pobres resultados que se obtienen con la función Uniform, este parámetro pareciera tener poca influencia en el comportamiento del método. Esto no significa que no sea importante. Significa que cualquier valor adoptado es una buena opción. No obstante, para poder obtener una respuesta más clara de cuál sería la mejor opción, al final de la sección se hará un experimento similar, pero con los otros parámetros fijados con sus valores óptimos (parámetros ajustados).
Opciones de reproducción
Una vez seleccionados los padres, mediante los parámetros de reproducción se especifica la manera de generar hijos para la siguiente generación. Esta puede ocurrir de tres formas principales. El elitismo asegura que un número determinado de individuos sobreviva y pasen tal y como son, hacia la siguiente generación. Evidentemente, los que sobreviven son los mejores adaptados. La segunda, y más común forma de reproducción es mediante el cruzamiento. CrossoverFraction especifica la cantidad de nuevos hijos que serán creados mediante la función de cruzamiento. Los padres son seleccionados mediante la función de selección previamente analizada. Los “hijos” restantes se obtienen mediante mutaciones. Es decir que, del 100 % de los nuevos hijos, un porciento será obtenido mediante elitismo, otro será definido mediante CrossoverFraction y el otro mediante mutaciones.Tabla 4 Figura 10
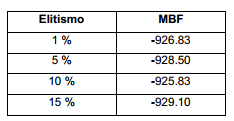
Referido al elitismo, este parámetro, para los valores analizados, tiene poca influencia en el rendimiento del método. Claro está, estos son los valores comúnmente manejados. Al agregar más posibles valores, seguramente los resultados empeorarían y se notara una gran diferencia. De cualquier manera, según la Figura 9 y la Tabla 3, la mejor opción es establecer un elitismo del 15 % del tamaño de población. Esto obedece igualmente al uso de grandes tamaños de población.
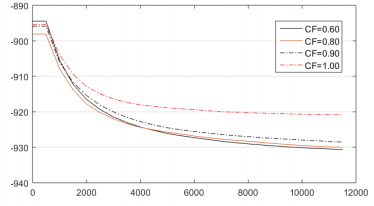
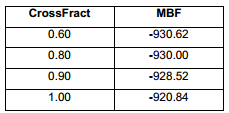
La fracción de cruzamiento, al igual que el elitismo, presenta diferentes rendimientos a lo largo del proceso. De manera general, la mejor opción resulto ser 0.60. Esto significa que el 60 % de la nueva población será formada por cruzamiento. Se puede apreciar que este valor es el que más pobres resultados ofrece en los primeros conteos de función, al igual que sucede en el análisis del elitismo.
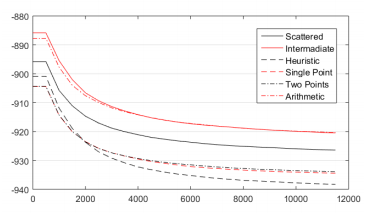
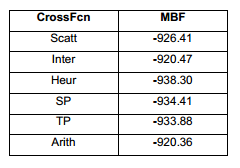
La función de cruzamiento condiciona como se hará el entrecruzamiento genético entre los dos padres seleccionados. Según la Figura 11 y la Tabla 5, evidentemente la mejor opción resultó ser la heurística. En (Dillen, y otros 2018) se obtiene, para la optimización estructural (problemas extremadamente complejos), la misma manera de realizar los cruzamientos como mejor opción. Esto demuestra que esta solución suele ser la más eficiente para enfrontar problemas de difícil solución.
Segundo análisis de opciones de selección
Una vez ajustado los parámetros, todavía quedaba la duda de cuál era la mejor opción para realizar la selección de los padres. Una vez establecidos los mejores valores de cada parámetro, se procede a realizar las pruebas para encontrar la función de selección idónea para enfrentar este tipo de problemas.Tabla 6
Lo que sucede aquí es realmente sorprendente. Lo que anteriormente era la peor opción, resulta ser, en esta nueva configuración, la mejor, con diferencia. Esto significa que, este método de selección ofrece muy pobres resultados con otras combinaciones de valores de otros parámetros. Sin embargo, para esta configuración, el cambio es sorprendente. Si observamos la Figura 8 y comparamos con la Figura 12, se puede apreciar la gran diferencia. Esto demuestra que este tipo de procedimientos suelen ser muy útil. Digamos que se hubiera establecido la configuración sin tener en cuenta este nuevo aspecto. Los resultados, al combinar la mejor configuración de los otros parámetros con esta función de selección son significativamente superiores. Esa es la gran ventaja de este tipo de estudios. Procedimientos de optimización mucho más eficientes, con resultados óptimos y racionales.
Aplicación de las estrategias propuestas
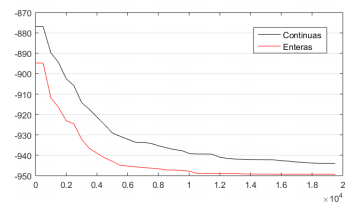
En la Figura 13 se puede apreciar la gran ventaja de aplicar la primera estrategia propuesta, el uso de variables discretas. Esta opción reduce significativamente el espacio de soluciones, por lo que la búsqueda se hace más fácil. La desventaja aquí es que el óptimo global, en funciones continuas, generalmente no está
en una “localización discreta”. Esto se puede resolver con una estrategia propuesta en (Negrin, y otros 2019b), donde se realiza una hibridación de GA simple con un método de búsqueda local. Es decir, GA simple utilizando variables enteras realiza la búsqueda en el espacio de soluciones, encontrando el “hueco” que contiene la mejor solución, que se alcanza con variables continuas. Luego, ese punto “discreto” obtenido por GA simple se brinda como punto de inicio a un algoritmo de búsqueda local utilizando variables continuas, el cuál encontrará la mejor solución global.Tabla 7
Por su parte, el método compuesto tiene como desventaja que consume un poco más de tiempo computacional, debido al proceso de búsqueda de la población inicial. Con una buena población inicial generada, se puede disminuir el tamaño de población del algoritmo de búsqueda general, con un significativo ahorro de recursos computacionales en esta etapa. Es decir, el método compuesto es un poco más costoso que los procedimientos simples aplicados, ya que, aunque el procedimiento de búsqueda general es más ligero, la búsqueda de la población inicial lo encarece en su conjunto.
GA simple ajustado utilizando variables continuas encontró el óptimo global el 30 % de las 20 pruebas. GA
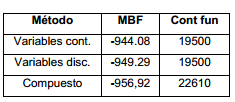
con variables enteras encontró “su” óptimo global el 90 % de las pruebas. Recordar que este óptimo global es lo mejor que este algoritmo con variables enteras puede encontrar, el cual evidentemente está muy cerca del óptimo global “continuo”. En la tabla 7 se puede apreciar, además, que el método compuesto fue capaz de encontrar el óptimo global el 100 % de las veces, a costa de un pequeño aumento del 16 % del costo computacional.
CONCLUSIONES
Los métodos de optimización presentan una serie de parámetros que regulan su funcionamiento. En la práctica, existen innumerables procesos que pueden ser optimizados. Cada uno de estos genera condiciones diferentes, entiéndase cantidad y tipos de variables, restricciones, superficies de respuesta, etc. Es de suponer que un mismo método puede presentar rendimientos diferentes ante diferentes problemas. Este rendimiento se puede regular, para hacerlo óptimo, ajustando dichos parámetros. Este proceso se denomina ajuste de parámetros (parameter tuning en inglés). Puede ser muy beneficioso, pero también muy tedioso y difícil de implementar, debido al enorme gasto computacional que demanda. Por otra parte, existen procesos de optimización que son extremadamente costosos, como la optimización estructural, en los cuáles ajustar los parámetros del método utilizado es casi imposible. Una manera de evitar este inconveniente es utilizar funciones analíticas, o de referencia, las cuales presentan características particulares, por lo que, en función del proceso de optimización real, se puede seleccionar una de ellas, y usarla como caso de estudio para ajustar los parámetros. La configuración obtenida es la que se utilizaría en la optimización del problema real.
En este trabajo se utilizó la función Eggholder, la cual es extremadamente difícil de optimizar pues presenta muchos óptimos locales, para ajustar los parámetros de los GA. La mejor configuración obtenida fue fijando un tamaño de población de 500 individuos, realizando la selección uniforme, un cruzamiento heurístico, con un elitismo del 15% del tamaño de población y una fracción de cruzamiento de 0.60.
Aún con el método ajustado, GA simple fue incapaz de encontrar el óptimo global regularmente. Debido a esto se proponen dos alternativas: el uso de variables discretas en vez de continuas, y un método compuesto basado en la generación de una población inicial utilizando el propio GA simple. La primera propuesta resultó ser bastante efectiva. Sin embargo, utilizando la segunda se fue capaz de encontrar el óptimo global el 100% de las pruebas, con un simple incremento del 16% del costo computacional.