Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El Problema de Empaquetamiento con Costo y Tamaño Variables (Variable Cost and Size Bin Packing Problem, VCSBPP) es una modificación propuesta por Crainic et. al. (Crainic et al., 2011) a la definición original de Friesen y Langston (Friesen y Langston, 1986). Consiste en empacar un conjunto de ítems en un conjunto de contenedores de varios tipos (tamaños) donde para cada tipo de contenedor existe una colección infinita (de manera que todos los ítems puedan ser empaquetados en un solo tipo). El objetivo del problema es minimizar el costo de todos los contenedores usados. Este problema tiene importantes aplicaciones en informática y telecomunicaciones (Kalaskar, 2013), logística (Crainic et al., 2014), entre otras.
Numerosos trabajos han propuesto métodos de solución aproximados (Fraire-Huacuja et al., 2019) para instancias de gran tamaño. Sin embargo, la aplicación de este problema en situaciones de la vida real ha demostrado la pertinencia de relajar determinadas restricciones según convenga. En este sentido, la introducción de los conjuntos difusos o borrosos (Ebrahimnejad y Verdegay, 2018) apunta a una necesidad latente de ajustar los modelos matemáticos a las condiciones reales de su aplicación. Existen muchos trabajos que abordan problemas importantes en el enfoque difuso como los relacionados con sistemas de transporte (Shavarani et al., 2019), redes (Mohammed et al., 2020), entre otros.
En el caso del VCSBPP, existen aproximaciones desde varios ángulos (Crainic et al., 2014) (Wang, Li y Mehrotra, 2019). Recientemente, en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020) se propone un modelo difuso relajando la restricción correspondiente a la capacidad de los contenedores y se comparan los resultados obtenidos con un solver (SCIP) y las heurísticas First Fit Decreasing (FFD) y Best Fit Decreasing (BFD). Ambos algoritmos parten de la condición de que tanto la lista de ítems como la lista de contenedores estén ordenadas descendentemente por los pesos de los ítems y las capacidades de los contenedores, respectivamente. El FFD coloca cada ítem en el primer contenedor donde cabe, mientras que el BFD selecciona entre todos los contenedores disponibles, aquel que después de empaquetar tiene el menor espacio vacío (Pillay y Qu, 2018). En el trabajo referenciado (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020), se utiliza el enfoque paramétrico propuesto por Verdegay (Ebrahimnejad y Verdegay, 2018), para encontrar la solución del problema difuso, compuesto por un conjunto de diferentes soluciones con diferentes grados de cumplimiento de las condiciones originales. Dicho enfoque introduce un problema adicional: el muestreo de la mayor cantidad de valores de pertenencia de las soluciones sin duplicados (Torres, Pelta y Teresa Lamata, 2018), de tal manera que pueda obtenerse el mayor conjunto de soluciones con diferentes compromisos entre el grado de pertenencia y el costo que pueda utilizar un decisor.
Varios autores utilizan este enfoque en problemas difusos como el caso de Chakraborty y Ray (Chakraborty y Ray, 2010) que abordan un problema difuso de ubicación de carbón mediante el enfoque paramétrico donde muestrean instancias empíricamente y utilizan el Algoritmo Genético Multiobjetivo para resolver cada una de estas. También, (Naseri y Khazaei, 2018) estudian un problema de programación fraccional lineal multiobjetivo con las variables difusas y proponen un algoritmo basado en el enfoque paramétrico donde el valor de pertenencia de cada solución se obtiene a partir de las instancias resueltas por el método que proponen. Por su parte, (Stanojevic y Stanojevic, 2020) investigan la clase de problemas de optimización lineal multiobjetivo con coeficientes difusos en las funciones objetivo para lo cual se basan en el enfoque paramétrico para calcular los valores de pertenencia de los puntos extremos en la solución del conjunto difuso para tales problemas.
En la bibliografía revisada no se encontraron evidencias de un método de muestreo que permita la solución del problema VCSBPP difuso y obtener el conjunto de soluciones con diferentes compromisos entre costo y pertenencia, a partir de enfocarlo como un problema multiobjetivo. Actualmente, los valores de pertenencia se establecen de forma empírica y en base a ellos se propone la solución difusa, es decir, se crean conjuntos de instancias con diferentes valores de relajación que conducen a la misma cantidad de soluciones que conforman la solución al problema difuso. Dado que los alfa-cortes (valores límites de pertenencia de cada instancia) se fijan arbitrariamente puede ocurrir que algunos valores de relajación no impliquen una mejora en costo respecto a una solución menos relajada, por lo que no serían de interés para un decisor.
En el presente trabajo se propone un enfoque multiobjetivo para el problema difuso propuesto en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020) y basado en metaheurísticas multiobjetivo. Este enfoque se basa en permitir que la búsqueda explore a la vez el espacio de relajaciones y de soluciones, y se evalúan las segundas según dos objetivos: costo y pertenencia. Además, se estudia la capacidad de varias metaheurísticas para resolver el problema multiobjetivo presentado.
El trabajo está organizado de la siguiente forma. En la sección “Métodos” se describe el problema abordado, el conjunto de instancias estudiadas, los algoritmos (parametrización y operadores), así como las medidas de calidad utilizadas en la evaluación de sus resultados. En la sección “Resultados y discusión” se muestran y discuten los resultados obtenidos y finalmente en la sección “Conclusiones” se exponen las ideas principales derivadas de los análisis anteriores.
MÉTODOS
El VCSBPP consiste en empacar un conjunto de ítems en un conjunto de contenedores de varios tipos (capacidad) y con una cantidad infinita de cada tipo, minimizando el costo de todos los contenedores usados. El modelo considerado fue propuesto en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020) donde se introduce una relajación en la capacidad de los contenedores.
Siguiendo una línea similar a otros trabajos (Haouari y Serairi, 2009) se utilizaron cuatro formas de relacionar la capacidad de cada tipo de contenedor con su costo: Lineal que se define como nx+m, Proporcional de la forma 0.1x, Cóncava como 
y finalmente Convexa, definida como 
. El tipo de relación Proporcional fue utilizada en (Herrera-Franklin, Rosete, García-Borroto y Cabrera-García, 2020) donde se estudia el impacto que tiene en la complejidad de las instancias.
Conjunto de instancias
Se definió un primer grupo de instancias, compuesto por las tres de base publicadas en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020) considerando valores de tolerancia fijos como está descrito en ese trabajo. Un segundo grupo de instancias incluye las propuestas en (Herrera-Franklin, Rosete, García-Borroto y Cabrera-García, 2020) de la cuales se consideraron las que siguen las distribuciones uniforme, normal y weibull en los pesos de los ítems.
Finalmente se conformó un tercer grupo que contiene 18 instancias siguiendo las pautas de (Correia, Gouveia y Saldanha-da-Gama, 2008), combinándolas de la siguiente forma:
Cantidad de ítems i ∈ {25, 50, 100}, pesos de los ítems [1-100], 3 tipos de bines con capacidades W = {100,120,150}, función de costo lineal donde costo = capacidad. 3 instancias.
Cantidad de ítems i ∈ {100, 200, 500}, pesos de los ítems [1-250], 7 tipos de bines con capacidades W = {70,100,130,160,190,220,250}, tres funciones de costo (Lineal, Cóncava y Convexa). 9 instancias.
En resumen, se utilizó un conjunto de 33 instancias que generalizan las características de las que se han publicado para estudiar las diferentes aristas del VCSBPP y está disponible en https://drive.google.com/drive/folders/1-5ogjSnxhJp6le8Ig0etoxNiiQRmPAKa?usp=sharing.
Representación de la solución
La representación de la solución consiste en un vector de longitud igual a la cantidad de ítems donde cada elemento que se corresponde con un ítem, contiene el índice del contenedor donde es empaquetado, es decir, cada solución es un vector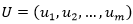 
, donde cada u 𝑖 indica la posición del contenedor donde se ubica el ítem i.
Configuración de los algoritmos
El objetivo de la presente investigación no es comparar el desempeño de determinados algoritmos para un problema específico, sino corroborar que el enfoque propuesto puede ser más eficiente que el enfoque tradicionalmente aplicado. En este sentido, las instancias descritas en la sección anterior fueron resueltas utilizando algunos de las metaheurísticas multiobjetivo más citadas en trabajos similares (Mohamed, Said y Lakhdar, 2012; Gobbato, 2014; Mann, 2015) en el contexto de problemas de empaquetamiento o asignación. Si bien, los algoritmos utilizados en los trabajos referenciados no son garantía de ser las mejores opciones para el problema abordado, se prefirió continuar esta línea considerando la disponibilidad de su implementación en la biblioteca de clases BiCIAM (Calderín-Fajardo, 2016).
De esta forma, fueron seleccionadas dos metaheurísticas basadas en un punto, la Búsqueda Local Multiobjetivo (MOLS por sus siglas en inglés) (Pillay y Qu, 2018) y el Recocido Simulado Multiobjetivo Ulungu (UMOSA por sus siglas en inglés) (Biswas y Acharyya, 2020) y de las poblacionales fue seleccionado el Algoritmo Genético Multiobjetivo (MOGA por sus siglas en inglés) y la variante conocida como NSGA-II (Alioui y Acar, 2020). Para el Recocido Simulado se utilizaron los parámetros establecidos en (Amine, 2019) quedando la Tinicial = 500, Tfinal = 0, alfa = 0.9 y la cantidad de iteraciones para la temperatura 500. Por otro lado, en la configuración de los algoritmos genéticos quedó como tipo de selección “torneo”, probabilidad de mutación 0.8, probabilidad de cruzamiento 0.5 y en el caso de Algoritmo Genético Multiobjetivo, el tipo de reemplazo establecido fue “generacional”. En todos los casos se establecieron 60000 iteraciones y 20 ejecuciones para cada instancia.
Operadores
Heurística de construcción de población inicial: Esta heurística es aplicada indistintamente tanto a las metaheurísticas poblacionales como a las basadas en un punto, buscando diversidad de soluciones factibles iniciales. Se basa en el FFD (Dósa y Epstein, 2018), solo que se genera un valor
donde para 0 se utiliza el FFD y para 1, la lista de contenedores se desordena, almacenando en una lista auxiliar el índice donde se encontraba originalmente cada contenedor y se aplica el First Fit (sin orden decreciente de capacidades). De esta manera, se van tomando uno a uno los ítems, y para cada uno se recorren los contenedores según el orden definido para ellos, colocando al ítem en el primer contenedor que quepa. Como el orden de los contenedores no siempre es igual, esto genera diferentes empaquetamientos.
Operadores de mutación: En todos los algoritmos se utilizaron dos operadores de mutación donde uno de ellos apunta a mejorar el costo de la solución actual y el otro el valor de membresía. Dado que este último requiere comprobar el valor de membresía de una solución, el tiempo de ejecución aumenta por lo cual, definió un esquema que hace que al inicio se utilice menos, según una probabilidad definida en (3):
(3)
donde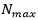 
es la cantidad máxima de iteraciones y 𝑁 𝑖 la iteración actual.
Operador de mutación para el costo: Esta heurística consiste en seleccionar un elemento del vector de solución actual y vaciar completamente el contenedor donde estaba ese elemento para obtener una lista de ítems que se ordena decrecientemente por sus pesos. Posteriormente se genera un valor de pertenencia aleatorio, que se utiliza para fijar la nueva capacidad de todos los contenedores según su tolerancia máxima, variándose paralelamente la membresía de la solución. A continuación, cada ítem en la lista, es re-empaquetado en el primer contenedor donde haya espacio exceptuando el contenedor de donde fue extraído, el cual no se utiliza.
Operador de mutación para la membresía: Este operador solo se puede ejecutar en soluciones con un valor de membresía menor que 1 para que exista algún tipo de sobrecarga en los contenedores que pueda modificarse. En este caso, se busca en el vector solución el primer ítem que apunte al contenedor que posea el valor de pertenencia más bajo, es decir, el más sobrecargado. De este, se extrae el ítem más pequeño de este y se re-empaqueta en un contenedor “abierto” donde quede más espacio y por supuesto, quepa el ítem en cuestión. El término “abierto” se refiere a un contenedor en uso ya que no tendría sentido abrir uno nuevo, pues se aumentaría el costo. Esta es la causa de seleccionarse el ítem más pequeño en el contenedor de menor pertenencia, ya que uno de los de mayor peso, podría no entrar en ninguno de los contenedores “abiertos” y desperdiciarse una iteración sin provocar cambios en la solución.
Operador de cruzamiento: Se utiliza cruzamiento uniforme (Hassanat et al., 2019), modificando todos los elementos del vector solución. Para esto se genera un vector binario aleatorio que indica si la solución hijo debe tomar la ubicación de cada ítem de un padre o del otro. Si el ítem seleccionado apunta a un contenedor que ya ha sobrepasado su capacidad total (considerando su tolerancia máxima) se almacena en una lista de “candidatos” que es procesada posteriormente para evitar que se genere una solución no factible. La heurística de reparación consiste en re-empacar la lista de candidatos utilizando el FFD. Al terminar este paso puede darse el caso de que aún queden elementos sin re-empacarse, por ejemplo, que en la lista de candidatos exista un ítem de los más grandes y todos los contenedores donde cabe estén ocupados total o parcialmente, de modo que no entre en ninguno de los existentes. En un caso así, para cada ítem pendiente, se busca el contenedor con el valor mínimo de la razón entre el peso del ítem y la capacidad del contenedor que no contenga un ítem mayor o igual que el pendiente. Este contendor es vaciado y el ítem en cuestión empacado en él mientras que los ítems que estaban contenidos, pasan a la lista de candidatos. Esta heurística se ejecuta recursivamente mientras existan elementos en la lista de candidatos.
Medidas de calidad para el rendimiento de los algoritmos
Para cada algoritmo se guardó el Frente de Pareto (Talbi, 2009) obtenido en cada ejecución. Posteriormente, con las soluciones de todos los frentes de todas las metaheurísticas en todas las iteraciones, se obtuvo un Frente de Pareto integrado, que se asume como una aproximación al frente real, a los efectos de las métricas. El perteneciente a cada ejecución se evaluó contra el aproximado considerándose el promedio de cada medida utilizada como métrica final para un análisis estadístico no paramétrico (Alcalá-Fdez et al., 2009). Se incluyeron el tiempo promedio de cada ejecución y la cantidad promedio de soluciones en el Frente de Pareto obtenidas. Además, se utilizaron tres indicadores de rendimiento pertenecientes a cada uno de los tres grupos definidos por (Audet et al., 2020): tasa de error, distancia generacional y dispersión.
RESULTADOS Y DISCUSIÓN
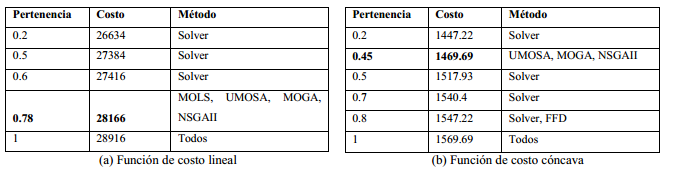
Los resultados correspondientes al primer conjunto de instancias, descrito en la sección anterior fueron resueltos utilizando el solver SCIP como se refleja en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al., 2020). Estos resultados fueron contrastados con los obtenidos por las metaheurísticas multiobjetivo (ver Figura 1) en cuanto al compromiso entre el costo y el grado de pertenencia de cada solución. Debe señalarse que el solver fue ejecutado durante una hora en la mayor parte de las instancias. Esto quiere decir que por cada instancia base se generaron 11 instancias crisp cuya mejor solución demoró una hora en encontrarse. Sin embargo, nótese que en la Figura 1(a) las metaheurísticas coinciden en una mejora del valor de pertenencia para un costo de 28166. Por otro lado, en la Figura 1(b) esta mejora se produce en casi todos los algoritmos para el costo 1469.69.
En este conjunto de instancias, el aspecto de mayor interés está en la cantidad de valores de pertenencia cercanos a los mejores que se obtuvieron con el solver y que, en algunos casos, mejoran con las metaheurísticas. Para ilustrar de otra forma la información que se muestra en la Figura 1, en la Tabla 1 se organizan los resultados por métodos organizados por los valores de pertenencia y costo obtenidos por cada uno. Los valores intermedios que se muestran en la Tabla 1 (por ejemplo 0.78 con costo 28166 para la función de costo lineal en la Tabla 1a y 0.45 con costo 1469 para la función cóncava en la Tabla 1b), donde las metaheurísticas mejoran la pertenencia, demuestran que existen valores difíciles de explorar manualmente y que las metaheurísticas son capaces de obtenerlos en poco tiempo. En este sentido vale la pena señalar el valor de costo 28166 que fue obtenido por el solver con un valor de pertenencia de 0.7, de manera que las metaheurísticas reflejadas lograron obtener una mejora que las hace competitivas con respecto al método exacto. Otro tanto ocurre para el valor de costo 1469.69, donde también se produjo una mejora ya que el valor de pertenencia que se obtuvo mediante el solver es de 0.4, aunque debe notarse que en este caso el MOLS fue el único que no obtuvo valores destacables.
Para evaluar la eficacia de las metaheurísticas en las 30 instancias de los grupos 2 y 3, se realizó el Test de Friedman utilizando la herramienta KEEL (Alcalá-Fdez et al., 2009) con los resultados de las medidas explicadas en la sección anterior. Los resultados de estas medidas, los análisis posteriores y los Frentes de Pareto obtenidos están disponibles en: https://drive.google.com/drive/folders/1-5ogjSnxhJp6le8Ig0etoxNiiQRmPAKa?usp=sharing. En la Tabla 2 se muestra el promedio de ranking obtenido en esta prueba, adicionándose una fila que muestra el p-value correspondiente a cada una de las medidas. Los mejores valores de ranking fueron resaltados para facilitar la interpretación de los resultados.
De manera general, se pudo comprobar que, el NSGAII muestra los mejores resultados desde el punto de vista de la eficacia, sin embargo, es el más lento, siendo lo contrario para el UMOSA. En el caso de la Tasa de Error, el Test de Friedman muestra que no existen diferencias significativas, lo cual se debe a que se obtuvo en casi todas las instancias un valor igual a 1 excepto en la instancia G3I2N50WeB3MaCv donde el MOLS obtuvo un valor de 0.933 y el UMOSA uno de 0.956. Considerando que, en las demás medidas los valores del Test de Friedman muestran diferencias significativas con p-values inferiores a 0.05, se realizó un análisis post-hoc mediante las pruebas de Holm, Finner y Li cuyos resultados se muestran en la Tabla 3.
Como puede comprobarse en la Tabla 3, los resultados de la medida de Dispersión indican que UMOSA es el peor para esta medida al tener diferencias significativas en todas las pruebas realizadas que confirman la posición obtenida en el Test de Friedman. Por su parte, la Distancia Generacional establece una diferencia sustancial entre los genéticos y los basados en un punto. En el caso, del MOGA la menor Distancia Generacional es 0.132 mientras que la del NSGA-II es 0.123 y las máximas son de 0.258 y 0.258 respectivamente. La medida de promedio de soluciones no dominadas por ejecución, refuerza la idea anterior por cuanto sigue obteniendo los mejores resultados el NSGA-II por con estrecho margen de diferencia con respecto al MOGA. Por tanto, considerando los valores de estos análisis para las medidas anteriores, puede apreciarse que el NSGA-II tiene mejor rendimiento de forma general. Nótese además que, en la Tabla 3 el NSGA-II solo aparece reflejado en la medida de Tiempo ya que, en el resto, el Test de Friedman lo coloca en primer lugar como se muestra en la Tabla 2.
Desde el punto de vista de la eficiencia, los genéticos sin lugar a dudas son los más lentos. El tiempo mínimo del UMOSA fue de 590.45 milisegundos mientras que para el NSGA-II fue de 5421.9 y los valores máximos fueron 39529.45 y 200352.45 respectivamente. Analizando los extremos, UMOSA es alrededor de 10 veces más rápido que NSGA-II, aunque este último tiende a obtener mejores soluciones. En la Tabla 3 se puede comprobar que, MOGA y NSGA-II tienen una diferencia sustancial de tiempo con respecto a UMOSA y MOLS que lo sigue en eficiencia. No obstante, aún en el caso de NSGA-II, el tiempo de ejecución máximo no supera los 2 minutos y obtiene un conjunto de soluciones de mayor calidad que UMOSA (Tabla 2). Por esto, el compromiso entre la calidad de las soluciones y el espectro de valores de pertenencia muestreados en tan poco tiempo se puede considerar que constituye una alternativa interesante respecto al método descrito en (Herrera-Franklin, Rosete, García-Borroto, Cruz-Corona, et al. 2020), en comparación con el tiempo superior a una hora que emplea el solver para resolver cada relajación asociada a un alfa-corte.
CONCLUSIONES
En el presente trabajo se aborda un problema difuso desde una nueva perspectiva que, permite obtener la solución difusa (varias soluciones con diferentes grados de relajación) en un tiempo razonablemente pequeño. La variante difusa del Problema de Empaquetamiento con Costo y Tamaño Variable (FVCSBPP) donde se permite una relajación en el tamaño de los contenedores solo ha sido abordada con el enfoque paramétrico de Verdegay, que implica muestrear empíricamente un conjunto de valores de pertenencia, lo cual introduce la posibilidad de perder valores mejores de pertenencia para soluciones con costos iguales. El enfoque del FVCSBPP como un problema multiobjetivo donde se minimiza el costo mientras se intenta aumentar la pertenencia de las soluciones, constituye el principal aporte de la investigación. Su aplicabilidad no se limita al FVCSBPP y a los problemas de la vida real que generaliza (logística, telecomunicaciones, procesos industriales, etc.), sino que puede ser extendido a otras familias de problemas de optimización como el Problema del Viajante, el Problema de Ruteo de Vehículos, entre otros, donde se utilice el enfoque paramétrico.
En los resultados experimentales se demostró que los operadores propuestos permiten un aumento del rendimiento en los procesos de exploración y explotación de las metaheurísticas utilizadas. Esto puede ser visto desde dos ángulos: la garantía de generar siempre soluciones factibles con amplia diversidad y su alta eficiencia ya que son basadas en la heurística FFD. Uno de los aspectos que debe ser abordado en el futuro, es basar los operadores propuestos en otras heurísticas de construcción para problemas de empaquetamiento, sin que se comprometa la eficiencia de los algoritmos. Entre las metaheurísticas utilizadas, sobresale en calidad el NSGAII a pesar de ser el más lento.
El método propuesto en el presente trabajo, no garantiza optimalidad, es decir, que se obtengan las mejores soluciones en cuanto a compromiso costo-pertenencia, para todos los valores de pertenencia donde sea posible. Sin embargo, como alternativa a las formas de abordar problemas difusos con el enfoque paramétrico tradicional, es muy recomendable por la reducción indiscutible. Nótese que el tiempo que toman los algoritmos para obtener soluciones mejores o al menos iguales que las obtenidas por un método exacto muestreando instancias manualmente, es notablemente inferior. De esta forma, el decisor puede obtener en menos tiempo que usando un solver, un conjunto de soluciones con un compromiso interesante entre costo y pertenencia.
