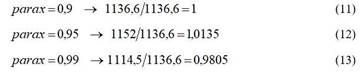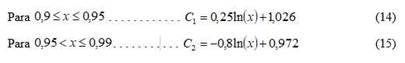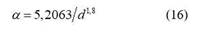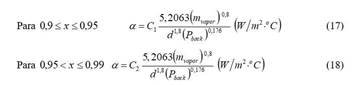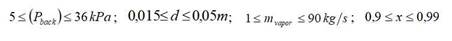Artículo original de investigación

Determinación de los coeficientes de transferencia de calor en aerocondensadores que operan en centrales eléctricas de biomasa

Determination of the heat transfer coefficient in air cooled condenser used at biomass power plants

0000-0003-2287-7519Yanán Camaraza Medina^{1  2  *}  , 0000-0002-4494-4965Oscar M. Cruz Fonticiella †²  , 0000-0001-5895-8033Osvaldo F. García Morales¹  , 0000-0002-0890-5475Ángel M. Rubio González² 

¹ Universidad de Matanzas. Matanzas, Cuba

² Universidad Central Marta Abreu de Las Villas. Santa Clara, Cuba

RESUMEN

Introducción:

El proyecto de centrales eléctricas (CE) de biomasa en Cuba enfrenta una limitante en la disponibilidad de agua para condensación. El aerocondensador (ACC) es la solución más difundida para reducir los índices de consumo de aguapara condensación y flexibilizar la ubicación de la CE. En el ACC la presión de agente de trabajo depende de variables ambientales, generando pérdidas de rendimiento y potencia. En la actualidad no se dispone de un método para estimar la relación entre la presión y el coeficiente de traspaso de calor. El objetivo de la investigación fue determinar cuál sería el rango de operación más adecuado de presiones y determinar analíticamente la causa de esta problemática.

Métodos:

Se hace uso de métodos matemáticos de superposición de variables cruzadas (Breshnetzov), para crear una correlación que sea capaz de predecir la influencia de la presión sobre el coeficiente de transferencia de calor en un ACC.

Resultados y discusión:

Mediante la superposición cruzada se establece la dependencia entre la presión, el coeficiente medio de transferencia de calor y las variables ambientales. La combinación de estas variables generadas expresiones no homogéneas, que permiten predecir con una precisión adecuada esta relación. Como conclusiones, se concluye que en el ACC la presión es inversamente proporcional al coeficiente de transferencia de calor en una potencia 0,176; reduciéndose este último en un 0,95 % por cada kPa incrementado en la presión de salida de turbina. El modelo propuesto fue correlacionado con 714 datos de instalaciones reales, obteniéndose una desviación media de ± 35,2 % en el 92,4 % de los datos.

Palabras-clave: método de Breshnetzov; coeficiente de transferencia de calor; variables independientes

ABSTRACT

Introduction:

The project of biomass power plants (EC) in Cuba has as limitation the access to water required by the condensation facilities. Air Cooled Condenser (ACC) is the most widely used solution worldwide to reduce the high rates of water consumption in condensation systems and make the location of the power plant more flexible. In the ACC the working agent pressure is affected by environmental conditions, which produces losses of performance and power. There is currently no method available to estimate the influence of pressure on the heat transfer coefficient in ACC. The objective of the research was to determine which would be the range of operation more adequate regarding pressures and to determine analytically the cause of this problem.

Methods:

A thematic method of superposition of crossed variables (Breshnetzov) is used to establish a correlation that is capable of predicting the influence of pressure on the heat transfer coefficient in ACC.

Results and discussion:

By means of crossed superposition is defined the dependence between pressure, heat transfer coefficient and environmental conditions. The combinations of these variables generate two non-homogeneous expressions, which allow us to predict this relationship with adequate fit. As some conclusions, the ACC pressure is inversely proportional to heat transfer coefficient in potency 0,176; decreasing this in 0,95 % for each kPa of increment in the back pressure of steam turbine. The proposal model was correlated with data of 714 ACC facilities, was verified that the mean deviation is ± 35,2 % in 92,4 % of available data.

Key words: Breshnetzov’s method; heat transfer coefficient; independent variables

INTRODUCCIÓN

En la actualidad es un criterio generalizado en la literatura especializada, el establecer que, en la operación de los aerocondensadores (ACC) son inadmisibles desde el punto de vista técnico económico las presiones de trabajo superiores a los 30 kPa. ¹ Recientemente fue planteado, ^2,3 que el valor máximo permisible es de 25 kPa. Varios reportes de instalaciones reales han confirmado que la operación de un ACC a estas presiones muestra pérdidas apreciables de rendimiento y potencia. Estos valores de presión límites son dados, por tanto, en base a criterios y experiencias acumuladas en la operación de la tecnología, sin embargo, la literatura disponible y conocida carece de un criterio científico que avale tal afirmación.

Cuba no está exenta de la crisis global de agua que enfrenta en la actualidad la humanidad y es necesario el empleo óptimo de este vital recurso. Un pilar para tal propósito es el uso de la tecnología de condensación seca, al prescindirse de 160 m³/h de agua como promedio por cada 50 MW de potencia generada. Sin embargo, en estas instalaciones la presión de agente de trabajo es afectada por variables ambientales, por esta razón estas instalaciones operan a presiones del vapor hasta 2,2 veces superior a la obtenida con su equivalente húmedo de un pase. ⁴

Las ecuaciones y métodos de análisis existentes y conocidos en la actualidad no permiten predecir la influencia de presión en la evaluación térmica del ACC. Esta limitante es la causa que motiva al autor y a sus colaboradores a profundizar en el tema, para determinar cuál sería el rango de operación más adecuado de presiones y determinar analíticamente la causa de esta problemática. Para esto se toma como punto de partida el empleo de métodos de análisis estadístico que acuden a la convergencia de funciones que pueden ser aproximadas mediante asíntotas continuas. Para este propósito fue seleccionado el método de cuerdas cruzadas de Breshnetzov, muy utilizado en la termotecnia cuando es requerido correlacionar varias variables independientes. ^5,6

MÉTODOS

Elementos introductorios de análisis

Recientemente fue demostrado que el coeficiente de transferencia de calor presenta un decrecimiento acentuado a partir de una presión igual a 20 kPa, encontrándose además que el en el rango de presiones 5 ≤ P _Back < 36 kPa manifiesta una clara tendencia regida por un funcional continuo tipo potencial. ⁷

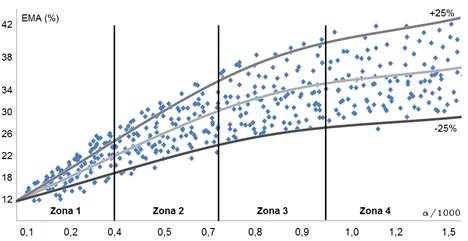
En el análisis efectuado fue encontrado que esta combinación interviene directamente la calidad, caudal y presión del vapor incorporado al ACC, así como el diámetro equivalente de los conductos en el ACC. El intervalo de presiones estudiado fue fragmentado en cinco regiones, en las cuales el coeficiente de transferencia de calor (α) muestra una clara tendencia asintótica decreciente, regida por una línea recta con cierta pendiente negativa con respecto a la horizontal (figura 1). Las 5 regiones son: ⁸

Fuente: Elaboración propia

Fig. 1 Tendencia asintótica y ángulo de barrido del coeficiente α en función de la presión. 

En todos los casos las asíntotas son lineales y de pendiente negativa. La curva experimental representada en la figura 1 es la que se obtiene como mejor ajuste a los datos experimentales que le dieron origen. ⁹ El coeficiente 𝛼 decrece con el incremento de la presión, sin embargo, es desconocida esta cuantía. En el ACC, la presión de salida de turbina es dependiente de temperatura de bulbo seco (T _TBS ) y de la velocidad del viento incidente (V _V ). Este problema fue tratado con anterioridad, siendo generados un grupo de expresiones que permiten obtener su valor numérico, las cuales vienen dadas por las relaciones siguientes: ^10,11

Aplicación del método de Breshnetzov

Ya conocida la presión P _Back del vapor a la salida de turbina, es requerido disponer además del caudal, la calidad del vapor a la entrada del ACC y el diámetro interno equivalente de los tubos de las celdas. Como el problema fundamental a estudiar consta de 4 variables independientes su correlación en una expresión única que sea lo suficientemente precisa deviene en una labor compleja, razón por la cual se acude al método de superposición cruzada de variables o método de Breshnetzov. ^12,13

En este método se toma al azar del grupo de variables independientes, la cual es correlacionada con la variable dependiente, siendo consideradas constantes el resto de las variables independientes, para posteriormente de forma cruzada establecer el nivel de participación de las restantes variables independientes en una cuantía fija que se preestablece a partir de la primera correlación generada.

Acá la variable dependiente es el coeficiente medio de transferencia de calor, mientras que las variables independientes son: presión del agente de trabajo a la salida de turbina (kPa), calidad del agente de trabajo a la salida de turbina (0-1), caudal del agente de trabajo (kg/s), diámetro interno equivalente de los conductos del condensador (m).

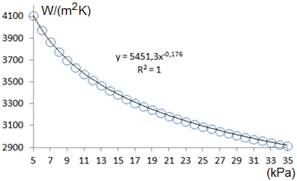
Tal como establece el método de Breshnetzov, se parte de establecer la condición primaria, acá se toma para este fin a la presión del agente de trabajo, (aunque puede ser tomada cualquier variable independiente) y es establecido un ajuste correlativo entre la variable dependiente y la primera variable independiente considerada, mientras que el resto de las variables son fijados sus valores de forma arbitraria, (acá se fijan en: d = 0,025 m, m _vapor = 1 Kg/s y x). La correlación establecida entre la presión y el coeficiente medio de transferencia de calor es dada en la figura 2.

Por lo tanto, es posible establecer una relación de tipo potencial entre el coeficiente de transferencia de calor y la presión del vapor de condensación. La relación obtenida responde a la siguiente expresión:

Fuente: Elaboración propia

Fig. 2 Ajuste inicial del coeficiente medio y la presión de salida de turbina. 

En la ecuación (7) la constante del numerador incluye el efecto de las 3 variables independientes restantes. En el segundo paso se establece la relación cruzada entre las variables restantes menos 1, y como restan 3 variables, entonces son 2 las que serán utilizadas para establecer la relación cruzada. Las 2 variables tomadas acá, serán las variables caudal y calidad del vapor. La función primaria establecida (7) para la correlación fue de tipo potencial, entonces es obligatorio el empleo de este tipo de función en los análisis restantes.

En la deducción de (7) fue variada la presión para un valor prefijado de caudal y calidad del vapor. Ahora manteniendo fijo el denominador de (7), se cambian en saltos los valores del caudal y la calidad del vapor, y al igual que en la deducción de (7), es efectuada una correlación entre el coeficiente de transferencia de calor y los valores de presión, para cada nuevo valor de caudal y calidad del vapor, fijado en cada salto iterativo.

Como en cada caso es establecida una nueva correlación, es requerido que sean tabulados los valores del numerador de la nueva relación potencial obtenida en cada caso, y como son consideradas 2 variables independientes, entonces son requeridas n + 1 combinaciones de una variable en función de la segunda. La calidad del vapor en la salida de turbina al ACC varía entre 0,9 y 0,99. Como es un intervalo pequeño, es esta la variable seleccionada y los 3 intervalos examinados serían 0,9, 0,95 y 0,99, mientras el caudal es variado en un espectro mayor, o sea, de 1 kg/s a 90 kg/s. Para este proceso se utiliza la herramienta computacional Microsoft Excel 2010. Los resultados obtenidos son dados en la tabla 1.

Ya con los valores de constantes cruzadas obtenidas a partir de los 3 intervalos requeridos, se puede establecer en cada caso, la correlación generada para cada salto cruzado. El método empleado establece que en los saltos cruzados de variables si una parte de la expresión de correlación es prefijada, en todos los casos es requerida y obligatoria la coincidencia de la parte prefijada. ^14,15

Tabla 1 . Valores fijos del numerador de (7) en la combinación cruzada 

	Calidad del vapor				Calidad del vapor
Caudal (kg/s)	0,9	0,95	0,99	Caudal (kg/s)	0,9	0,95	0,99
1	1136,8	1151,9	1114,8	30	17 272	17 502	16 931
3	2 736,7	2 774,4	2 683,8	35	19 539	19 799	19 154
5	4 119,1	4 174,9	4 037,4	40	21 743	22 032	21 313
8	5999	6080,8	5881	50	25 990	26 338	25 480
12	8299,4	8407,6	8135,4	60	30 074	30 473	29 478
16	10 446	10 584	10 240	70	34 020	34 471	33 347
20	12 487	12 653	12 241	80	37 855	38 359	37 108
25	14 928	15 127	14 633	90	41 596	42 150	40 773

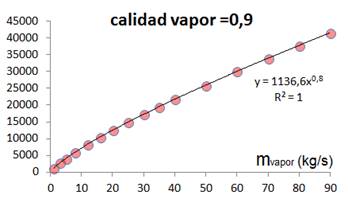
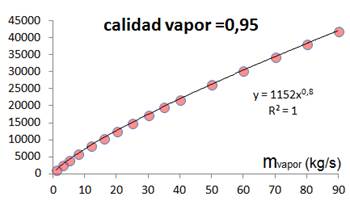
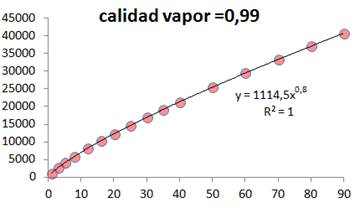
Variando el caudal para 3 valores fijos de calidad del vapor (tabla 1), estableciendo como obligatorio el empleo de una función potencial como curva de ajuste, (lo cual es requerido por ser esta la primera función de correlación empleada) y prefijando una cuantía o valor fijo en función de la variable cambiante (caudal) igual a (m_vapor)^0,8 se obtienen 3 juegos de ajustes los cuales son graficados en las figuras 3 a la 5. Tal como se puede comprobar se cumple en los 3 casos la condición impuesta (m_vapor)^0,8, disponiéndose finalmente de 3 nuevas expresiones, que quedan dadas por:

En las ecuaciones (8) a la (10) se tienen 3 constantes para valores ascendentes de la variable independiente empleada en el análisis cruzado, por tanto se toma la primera cantidad como referencia unitaria, mientras que las 2 restantes crecen o decrecen proporcionalmente con respecto a la cuantía unitaria, -o sea:

Fuente: Elaboración propia

Fig. 3 .Correlación entre el numerador de la expresión (7) y el caudal de vapor, para x = 0,9. 

Fuente: Elaboración propia

Fig. 4 .Correlación entre el numerador de la ecuación (7) y el caudal de vapor, para x = 0,95. 

Fuente: Elaboración propia

Fig. 5 .Correlación entre el numerador de la ecuación (7) y el caudal de vapor, para x = 0,99. 

Como en el análisis cruzado fueron empleadas 2 variables independientes, entonces se requieren de 2 intervalos en la correlación forzada de la tercera variable. Estos intervalos son:

Un detalle importante, la correlación de la última variable involucrada en el análisis cruzado admite cualquier tipo de funcional, siempre y cuando sea reducible al primero empleado, o sea a una ecuación potencial. ¹⁶

Combinando convenientemente las constantes dadas en las ecuaciones (11) a (13) con las calidades del vapor que le generan se tiene que:

Solo resta una variable por considerar, el diámetro equivalente. Acá se efectúa un ajuste de correlación bajo las mismas condiciones primarias que propiciaron la obtención de la relación, ⁷ pero como a lo largo del análisis fue fijado el valor del denominador, ahora es requerido analizar en la superposición final la variación del numerador en función de la última variable, prefijando las restantes variables bajo las condiciones iniciales del problema analizado. Esto se justifica al tener en cuenta que el valor del numerador es igual a una función arbitraria que involucra las variables independientes no consideradas en el análisis inicial. La variación del diámetro equivalente para condiciones fijas de caudal y calidad del vapor establecido al inicio generan un grupo de valores, los cuales son tabulados en la tabla 2. ¹⁷

Para la correlación entre diámetro y la constante del numerador se acude a una función potencial, la cual con un R²=1, queda descrita por la siguiente expresión:

La correlación (16) es representada gráficamente en la figura 6.

Por tanto, ya puede ser generada la expresión final, pero al ser usados 2 intervalos de análisis cruzado, esta tendrá 2 zonas de aplicación y por ende estará constituida también por 2 correlaciones.

Para la primera zona (0,9 ≤ x ≤ 0,95) fue demostrado que el denominador de (7) es igual al producto de las ecuaciones (16), (14) y la potencia (m _vapor )^0,8, mientras que para la segunda zona (0,95 < x ≤ 0,99) este se corresponde con el producto de las relaciones (16), (15) y la potencia (m _vapor )^0,8. En definitiva, se tiene que:

Las ecuaciones (17) y (18) fueron obtenidas por un método matemático de superposición de variables y son válidas para:

Tabla 2. Variación del numerador de (7) en función de la variable de superposición 

Diámetro (m)	Constante numerador (7)	Diámetro (m)	Constante numerador (7)
0,015	9 989,1	0,035	2 173,6
0,02	5 951,8	0,04	1 709,2
0,021	5 451,3	0,045	1 382,7
0,025	3 982,9	0,05	1 143,8
0,03	2 868,6

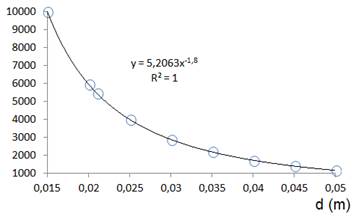Fuente: Elaboración propia

Fig. 6 .Correlación entre el numerador de la expresión (7) y el diámetro equivalente. 

En el denominador de (17) y (18) está presente el complejo (P _back )^0,176, lo que indica que en el ACC la presión es inversamente proporcional al coeficiente de transferencia de calor por condensación en una potencia 0,176. Por esta causa se reduce el coeficiente de transferencia de calor en un 0,95 % por cada kPa de incremento en la presión de salida de turbina, lo cual explica la proporcionalidad existente entre la penalización de la eficiencia del ACC y el incremento de la presión de salida de turbina.

RESULTADOS Y DISCUSIÓN

Las expresiones (17) y (18), son correlacionadas con 714 datos disponibles de instalaciones reales (figura 7), obteniéndose un error medio absoluto (EMA) de ± 35,2 % en el 92,4 % de los datos ⁹⁾ mientras en la figura 8 es graficada la correlación con datos reportados por otros autores. ^18,19

Fuente: Elaboración propia

Fig. 7 Comparación de las ecuaciones (17) y (18) con datos experimentales disponibles.  

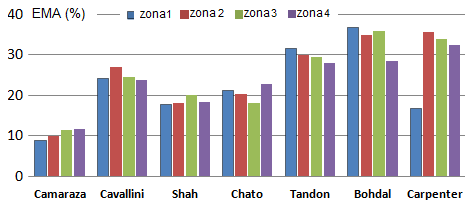Fuente: Elaboración propia

Fig. 8.  Correlación de las ecuaciones (17) y (18) con respecto a otros modelos conocidos. 

Conclusiones

Mediante el empleo de un método de cruzamientos de variables (Breshnetzov) se obtiene que para los intervalos de presiones situados entre 5 kPa a 36 kPa, el coeficiente de transferencia de calor experimenta decrecimientos asintóticos, tomando un comportamiento aproximadamente constante a partir de los 28 kPa, con un ángulo de inclinación de 6,3^o.

La combinación de variables independientes genera 2 expresiones no homogéneas, dependiendo de la calidad del vapor la zona de aplicabilidad de cada una. En el ACC la presión es inversamente proporcional al coeficiente de transferencia de calor en una potencia 0,176. Esto genera una reducción de este último del 0,95 % por cada kPa de incremento en la presión de salida de turbina.

Las expresiones (17) y (18), son correlacionadas con 714 datos disponibles de ACC, obteniéndose un error medio absoluto de ± 35,2 % en el 92,4 % de los datos.

Agradecimientos

Ing. Liván Nicolás Arronte Cruz (MINEM), Ing. Alexander Estrada Jaén, (UNE), Ing. Carlos Manuel Brunet Zamora (UNE), Dr. Manuel Alejandro Rubio Rodríguez (UCLV), Dr. Roberto Vizcón Toledo (UMCC), Dr. Jorge Luis Jiménez Hernández (CITMA).

REFERENCIAS BIBLIOGRÁFICAS

1.  Camaraza Medina Y, Retirado Mediaceja Y, Hernández Guerrero A, et al. Energy efficiency indicators of the steam boiler in a power plant of Cuba. Thermal Science and Engineering Progress. [Internet], 2021;23:100880. Disponible en: https://doi.org/10.1016/j.tsep.2021.1008801.

2.  Camaraza Medina Y, Sánchez Escalona A.A, Retirado Mediaceja Y, et al. New procedure for thermal assessment of an air cooled condenser coupled to biomass power plant. International Journal of Sustainable Development and Planning. [Internet], 2020;15(8):1297-302. Disponible en: https://doi.org/10.18280/ijsdp.1508162.

3.  Camaraza Medina Y, Hernández Guerrero A, Luviano Ortiz JL. Comparative study on heat transfer calculation in transition and turbulent flow regime inside tubes. Latin American Applied Research. [Internet], 2020;50(4):309-14. Disponible en: https://doi.org/10.52292/j.laar.2020.5803.

4.  Camaraza Medina Y, Rubio Gonzales AM, Cruz Fonticiella OM, et al. Analysis of pressure influence over heat transfer coefficient on air cooled condenser. Journal Européen des Systems Automatisés. [Internet], 2017;50(3):213-26. Disponible en: http://dx.doi.org /10.3166/jesa.50.213-2264.

5.  Camaraza Medina Y, Hernandez Guerrero A, Luviano Ortiz JL, et al. Mathematical deduction of a new model for calculation of heat transfer by condensation inside pipes. International Journal of Heat and Mass Transfer. [Internet], 2019;141:180-90. Disponible en: https://doi.org/10.1016/j.ijheatmasstransfer.2019.06.0765.

6.  Camaraza Medina Y, Hernandez Guerrero A, Luviano Ortiz JL, et al. New model for heat transfer calculation during film condensation inside pipes. International Journal of Heat and Mass Transfer. [Internet], 2019;128:344-53. Disponible en: https://doi.org/10.1016/j.ijheatmasstransfer.2018.09.0126.

7.  Camaraza Medina Y, Khandy NH, Carlson KM, et al. Evaluation of condensation heat transfer in air-cooled condenser by dominant flow criteria. Mathematical Modeling of Engineering Problems. [Internet], 2018;5(2):76-82. Disponible en: https://doi.org/10.18280/mmep.0502047.

8.  Medina YC, Khandy NH, Carlson KM, et al. Mathematical modeling of two-phase media heat transfer coefficient in air-cooled condenser systems. International Journal of Heat and Technology. [Internet], 2018;36(1):319-24. Disponible en: https://doi.org/10.18280/ijht.3601428.

9.  Camaraza Medina Y. Métodos para la evaluación de los coeficientes de transferencia de calor en aerocondensadores que operan en centrales eléctricas de biomasa. [Tesis doctorado]. Santa Clara: Universidad Central Marta Abreu de Las Villas; 2019. 100 p.

10.  Camaraza Medina Y, Rubio Gonzales AM, Cruz Fonticiella OM, et al. Simplified analysis of heat transfer through a finned tube bundle in air-cooled condenser. Mathematical Modelling of Engineering Problems. [Internet], 2018;5(3):237-42. Disponible en: https://doi.org/10.18280/mmep.05031610.

11.  Camaraza Medina Y. Current Trends in Cuba on the Environmental Impact and Sustainable Development. Italian Journal of Engineering Sciences. [Internet], 2020;64(1):103-8. Disponible en: https://doi.org/10.18280/ti-ijes.64011611.

12.  Camaraza Medina Y, Mortensen Carlson K, Guha P, et al. Suggested Model for Heat Transfer Calculation During Fluid Flow in Single Phase Inside Pipes (II). International Journal of Heat and Technology. [Internet], 2019;37(1):257-66. Disponible en: https://doi.org/10.18280/ijht.37013112.

13.  Camaraza Medina Y, García Lovella Y, Sánchez Escalona AA, et al. Suggested method for heat transfer calculation during film condensation inside pipes with movable frontiers. Mathematical Modelling of Engineering Problems. [Internet], 2019;6(3):449-54. Disponible en: http://doi.org/10.18280/mmep.06031713.

14.  Camaraza Medina Y, Sánchez Escalona AA, Retirado Mediaceja Y, et al. Use of air cooled condenser in biomass power plants: a case study in Cuba. International Journal of Heat and Technology. [Internet], 2020;38(2):425-31. Disponible en: https://doi.org/10.18280/ijht.38021814.

15.  Camaraza Medina Y, Hernandez Guerrero A, Luviano Ortiz JL, et al. New improvement model for heat transfer calculation on viscous-gravitational fluid flow inside vertical and inclined tubes. International Journal of Heat and Mass Transfer. [Internet], 2020;159:120108. Disponible en: https://doi.org/10.1016/j.ijheatmasstransfer.2020.120108.15.

16.  Camaraza Medina Y, Cruz Fonticiella OM, García Morales OF. New model for heat transfer calculation during fluid flow in single phase inside pipes. Thermal Science and Engineering Progress. [Internet] 2019; 11:162-6. Disponible en: https://doi.org/10.1016/j.tsep.2019.03.01416.

17.  Camaraza Medina Y, Sánchez Escalona AA, Retirado Mediaceja Y, et al. Proposal method for assessment evaluation of air cooled condenser used in a biomass power plant of Cuba. Italian Journal of Engineering Sciences. [Internet], 2020;64(2):202-6. Disponible en: https://doi.org/10.18280/ti-ijes.642-41117.

18.  Camaraza Medina Y. Methods for the determination of the heat transfer coefficient in air cooled condenser used at biomass power plants. International Journal of Heat and Technology. [Internet], 2021;39(5):1443-50. Disponible en: https://doi.org/10.18280/ijht.39050518.

19.  Camaraza Medina Y. New perspective for heat transfer evaluation during film condensation inside tubes, International Journal of Heat and Technology. [Internet], 2021;39(2):390-402. Disponible en: https://doi.org/10.18280/ijht.39020819.

Financiamiento

11El trabajo e investigación desarrolladas al efecto contaron con el apoyo financiero y logístico de la Empresa Eléctrica Matanzas (UNE) y la Empresa Azucarera Villa Clara (AZCUBA).

Recibido: 18 de Junio de 2022; Aprobado: 13 de Septiembre de 2022

^*Autor para la correspondencia: [e-mail]

Los autores declaran que no existen conflictos de intereses.

Conceptualización: Yanán Camaraza Medina

Análisis formal: Yanán Camaraza Medina.

Investigación: Yanán Camaraza Medina, Oscar Miguel Cruz Fonticiella, Osvaldo Fidel García Morales

Metodología: Yanán Camaraza Medina, Oscar Miguel Cruz Fonticiella, Osvaldo Fidel García Morales, Ángel Manuel Rubio González

Supervisión: Oscar Miguel Cruz Fonticiella, Osvaldo Fidel García Morales, Ángel Manuel Rubio González

Validación: Yanán Camaraza Medina

Visualización: Dr. Yanán Camaraza Medina, Oscar Miguel Cruz Fonticiella, Osvaldo Fidel García Morales, Ángel Manuel Rubio González

Redacción-borrador original: Yanán Camaraza Medina

Redacción-revisión y edición: Yanán Camaraza Medina, Oscar Miguel Cruz Fonticiella, Osvaldo Fidel García Morales, Ángel Manuel Rubio González