Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Retos de la Dirección
versión On-line ISSN 2306-9155
Rev retos vol.11 no.2 Camagüey jul.-dic. 2017
Optimización de los niveles de inventario con enfoque colaborativo en una cadena de suministros de servicios turísticos
Optimizing Inventory Levels with a Collaborative Approach in a Service Supply Chain in Tourism
MSc. Aliosky Camacho Rodríguez y Dra. C. Esther Lidia Machado Chaviano
Departamento de Turismo de la Facultad de Ciencias Económicas, Universidad Central Marta Abreu de Las Villas, Santa Clara, Villa Clara. acamacho@uclv.edu.cu
RESUMEN
La gestión de inventarios es un tema común cuando se estudia la gestión empresarial como elemento clave para optimizar el costo de operación de cualquier proceso productivo y/o prestación de servicio. Los modelos de inventarios tradicionales abordan la optimización de los niveles de inventarios para una organización individual, sin importar la relación de ésta, con el resto de la cadena de suministro de la que forma parte. En este aspecto, en la gestión empresarial la satisfacción del cliente final se logra mediante el cumplimiento de los flujos básicos de la cadena de suministros, de manera que se requieren niveles de cooperación e integración entre los participantes de la cadena en términos de inventario, con el objetivo de disminuir las pérdidas para cada parte y las mejoras en los costos totales de operación de sus sistemas de gestión. En este trabajo se estudia la optimización de los inventarios con un enfoque colaborativo, en empresas de servicios, mediante una visión justo a tiempo, de manera conjunta comprador-intermediario-proveedor. Se hicieron comparaciones con métodos tradicionales y se determinaron las ventajas de este enfoque colaborativo en los costos de inventario de la cadena de suministro y su incidencia en la satisfacción del consumidor final, a través de un caso de estudio.
Palabras clave: cadena de suministro, inventario, JIT, optimización.
ABSTRACT
Inventory management is a common topic when it comes to company management, as a key element to optimize operational costs in production and/or services. The traditional inventory models deal with optimization of inventory levels for a single organization, regardless of its relation with the rest of the supply chain it belongs. Accordingly, satisfaction of the final client is achieved through implementation of basic flows in the supply chain, which call for cooperation and integration among the different links in the chain, in terms of inventory. The goal is to cut down losses on each side, and improve total operational costs of their management systems. Therefore, this research focused on inventory optimization based on a collaborative approach for service providing companies, and it used a just-in-time perspective that binds together buyer-middleman-supplier. Comparisons were made using traditional methods to determine the advantages of the collaborative approach to deal with inventory costs in the supply chain. A study case was presented to identify the effects on final user's satisfaction.
Key words: supply chain, inventory, JIT, optimization.
INTRODUCCIÓN
"Lo siento, no tenemos". ¿Cuántas veces se escucha esta respuesta cuando se va de compras, o se hace un pedido en un restaurante?: En muchos casos, debido a que esas empresas no administran adecuadamente sus inventarios, lo que les imposibilita colocar sus pedidos de reabastecimientos con suficiente anticipación para evitar faltantes (Hillier y Lieberman, 2010).
La gestión de inventarios es una actividad compleja y un tema muy estudiado por la administración de operaciones (Schroeder, 2005; Hillier y Lieberman, 2010), para optimizar el costo de la gestión de la empresa, ya que para evaluarla no es posible tener en cuenta de forma aislada, indicadores y parámetros determinados, pues solo con una integración de resultados es posible determinar el nivel en que la empresa se encuentra (Kelle, Al-khateeb y Miller, 2003; Heizer y Render, 2009; Hillier y Lieberman, 2010; Taha, 2012; Lopes, Gómez y Acevedo, 2012).
El problema del inadecuado nivel de inventario a nivel empresarial, en la mayoría de las instalaciones turísticas del país, no se resuelve aplicando acciones que funcionen puntualmente, sino revisando la causa general. El inventario es el resultado del comportamiento de la gestión empresarial y la consecuencia del manejo de las relaciones empresariales. No puede verse solo como responsabilidad de un área, sino como un proceso en el que intervienen varios actores, que según De Vries (2007) incluyen: función de compras, ventas o comercial, logística, producción, finanzas e incluso la parte jurídica; todos influyendo en el nivel de excesos, faltas o la racionalidad que se desea (Lopes et al. 2012).
De lo anterior no resulta suficiente atender la gestión de los inventarios a nivel de empresa, pues es necesario enfocarlos a nivel de la cadena de suministro y las relaciones que se establecen entre los eslabones de esta, en busca de la integración de sus miembros para alinear los objetivos que, de forma común, satisfagan al cliente final (Wild, 2002; Aiello, 2008; Chase, Jacobs y Aquilano, 2009; Lopes et al. 2012). De ahí que una adecuada gestión de inventarios se logra con un funcionamiento apropiado de las relaciones empresariales y en el marco de la cadena de suministro, en la cual el papel del pronóstico de la demanda es fundamental en la proyección de los niveles óptimos de inventarios a manejar por la empresa (Heizer y Render, 2009).
En este período de investigación se ha trabajado en diseñar el proceso de balance de los inventarios (planificación de estos) como resultado necesario para su adecuada gestión, siempre a partir de estimar las demandas futuras de los productos que lo conforman, así como la forma en que esta se comporta; además, se ha demostrado que es posible planificar los inventarios sin alcanzar la efectividad requerida por las empresas de servicio estudiadas.
Los casos más trascendentales son los de las empresas de la hospitalidad, cuyos objetivos eran reducir los niveles de inventario y el resultado fue que, para tener inventarios balanceados o bien planificados (para un servicio eficiente), era necesario aumentar los niveles de estos, contrario a lo que la empresa esperaba. La explicación de este resultado se basa en que las estadísticas estaban asociadas a productos con bajos niveles de disponibilidad y ciclos inestables de aprovisionamiento, que tienen sus causas en la planeación ineficiente de la demanda y la inestabilidad de las entregas de los proveedores.
Lo anterior demuestra que si se aplica un procedimiento de balance de forma aislada, es posible lograrlo con altos volúmenes, los que son financieramente insostenibles, elevando la probabilidad de que los productos se conviertan en pérdidas, como en el caso de los diferentes tipos de alimentos que se manejan en las ofertas gastronómicas de un hotel o un restaurante, entre otros. Este análisis apoya la teoría de que, además de diseñar el balance de los inventarios, es necesario analizar el resto de los factores que influyen, ya que un inventario balanceado no implica eficiencia. La eficiencia de este está directamente relacionada al indicador de rotación, pero para lograr un resultado efectivo es necesario integrar su análisis con el criterio de disponibilidad, que es el indicador fundamental desde la perspectiva del cliente (Bowersox, 2007; Lopes et al. 2012).
A partir de los resultados y el estudio teórico, se considera que deben ser definidos los elementos de la organización y la gestión que inciden en el comportamiento de la efectividad del inventario, que permita a estas empresas ser eficientes con su oferta y al mismo tiempo que los niveles de satisfacción de sus clientes sean elevados (De Vries, 2007; Aiello, 2008; Lopes et al. 2012).
De todo lo anterior no cabe duda que la satisfacción de las necesidades del cliente final se logra mediante los flujos materiales, de información y financiero que se establecen a través de la cadena de suministros (Ballou, 2004; Díaz y Pérez, 2012) desde los proveedores originales hasta el último consumidor, lo que requiere determinado nivel de cooperación e integración entre los participantes en la cadena. En este trabajo se estudia la optimización de los inventarios conjuntos suministrador-proveedor, como eslabón básico de la cadena de suministros de productos para empresas turísticas, de manera que se compara con métodos tradicionales y se establecen las ventajas de este enfoque colaborativo en los costos totales de inventario en la cadena, y su incidencia en la satisfacción del consumidor final.
Sobre este tema se han realizado varios estudios centrados en los aspectos cualitativos de establecer y negociar asociaciones entre compradores y proveedores, incluido el justo a tiempo (just in time-JIT) (Gilbert, Young y O'Neal, 1994; Newman, 1988). Mientras, en otras literaturas de gestión son muy pocos los modelos cuantitativos e investigaciones disponibles orientados a optimizar inventarios en cadenas de suministro. El siguiente análisis desarrolla un ejemplo utilizando contribuciones de Pan y Liao (1989), quienes desarrollaron un modelo de tipo simple mediante lote económico (EOQ) para un sistema de suministro JIT, donde cada orden se entrega en n envíos al comprador (Kelle y Miller, 1998); para demostrar cuantitativamente las ventajas de la optimización de los inventarios conjuntos en el ambiente colaborativo de las cadenas de suministros.
Por otra parte el trabajo se fortalece con los aportes de Goyal (1988); Banerjee y Kim (1995); Kelle y Miller (1998); Kelle et al (2003); Díaz y Pérez (2012); Shah, Patel y Shah (2014) quienes desarrollan modelos para encontrar la cantidad más óptima de la orden conjunta para el comprador y el proveedor para facilitar la cooperación, con énfasis en sistemas de compras JIT y enfoques de operaciones esbeltas.
DESARROLLO
El análisis general de la teoría de inventarios
Los modelos para el control de inventarios suponen que la demanda de un artículo es independiente o dependiente de la demanda de otros artículos. Por ejemplo, la demanda de refrescos es independiente de la demanda de los platos que se ofertan en la carta de un restaurante. Sin embargo, la demanda de ingredientes para dichos platos es dependiente de las cantidades necesarias para la elaboración de dicho plato (Heizer y Render, 2009; Chase et al. 2009; Acevedo, 2010).
Por otro lado, los costos de inventario constituyen uno de los más importantes en la logística de muchas empresas y representan una parte significativa de su costo total. Tradicionalmente, la modelación y optimización de los inventarios en una empresa contemplaba solo los costos internos de esta, sin considerar la relación con sus suministradores (Schroeder, 2005; Heizer y Render, 2009; Chase et al. 2009; Acevedo, 2010; Díaz y Pérez, 2012).
El modelo clásico de inventario EOQ (economic order quantity) (Schroeder, 2005; Muckstadt y Sapra, 2010) es un ejemplo de ello. Este modelo se utiliza independientemente del tipo de demanda que presenten los productos.
El objetivo de la mayoría de los modelos de inventario es minimizar los costos totales; asimismo, los costos significativos en estos modelos son el de preparación (u ordenar) y el de mantener (o llevar). Todos los demás, como el costo del inventario en sí, son constantes (Aiello, 2008; Heizer y Render, 2009; Muckstadt y Sapra, 2010; Rushton, 2010; Díaz y Pérez, 2012). De esta forma, si se minimiza la suma de los costos de preparar y mantener, también se minimizaría el costo total.
Ahora, considérese el caso de un hotel (empresa I) que sigue este modelo con los siguientes términos:
D = Demanda anual en unidades para el artículo en inventario
C = Costo por unidad del producto (compra o producción)
S = Costo de ordenar o de preparación para cada orden
H = Costo de mantener o llevar en inventario una unidad por año (H = iC, donde i es un porcentaje del costo de manejo del inventario)
Q = Número de unidades por orden
Q* = Número óptimo de unidades a ordenar (EOQ)
Usando estas variables se pueden determinar los costos de ordenar y mantener, de los cuales se puede despejar Q*:
1. Costo anual de preparación (CO) (expresión 1) = (Número de órdenes colocadas por año) x (Costo de preparación u ordenar por orden)
2. Costo anual de mantener (CI) (expresión 2) = (Nivel de inventario promedio) x (Costo de mantener una unidad por año)
3. La cantidad óptima a ordenar se encuentra cuando el costo anual de preparación es igual al costo anual de mantener (expresión 3):
Entonces la cuantía del lote óptimo a pedir Q* es la conocida expresión 4:
Ésta corresponde a un costo mínimo total por año dado por la expresión 5:
Ahora, supóngase también la existencia de una empresa proveedora de dicho hotel (Empresa II) que cuenta con una capacidad de producción de P (unidades por año) para satisfacer D (la demanda anual antes mencionada). En este caso, el comportamiento del inventario, el modelo POQ es quien maneja los niveles de inventarios.
En los casos de los intermediarios que no producen e integran las cadenas de suministros en el sector turístico, como los mayoristas, el comportamiento de los niveles de inventario y los costos asociados a este se comportan de la misma forma que para el caso anterior.
Dado que este modelo es especialmente adecuado para los entornos de producción, se conoce como el modelo de la cantidad económica que se debe producir. Es útil cuando el inventario se acumula de manera continua en el tiempo y se cumplen los supuestos tradicionales de la cantidad económica a ordenar (Heizer y Render, 2009; Díaz y Pérez, 2012). Este modelo se obtiene igualando el costo de ordenar o preparar, al costo de mantener, y despejando el tamaño del lote óptimo Q*. En él aparecen los siguientes términos:
p = Tasa de producción diaria
d = Tasa de demanda diaria, o tasa de uso
t= Longitud de la corrida de producción en días.
Usando los siguientes términos es posible determinar la expresión del costo anual de mantener inventario para la cantidad económica a producir:
1. Costo anual de mantener inventario = (Nivel de inventario promedio) x (Costo de mantener una unidad por año)
2. Nivel de inventario promedio = (Nivel de inventario máximo) / 2
3. Nivel de inventario máximo (expresión 6) = (total producido durante la corrida de producción) - (Total usado durante la corrida de producción)
Imáx=pt-dt (6)
Sin embargo, Q = total producido = pt, y así t = Q/p., por lo tanto el nivel de inventario máximo se obtiene por la expresión 7:
De lo anterior se obtiene que el costo anual de mantener inventarios (expresión 8) para este modelo es:
Usando estas expresiones, igualando el costo de ordenar con el costo de mantener para obtener para este modelo, mediante la expresión 9.
Ésta corresponde a un costo mínimo total por año dado por la expresión 10:
Pero en una cadena de suministro el eslabón básico está constituido por la relación proveedor-comprador, por lo que si la empresa I es el comprador y la empresa II es el proveedor, entonces se puede comprender fácilmente que los tamaños del lote económico para el suministrador ( ) y para el comprador ( ) en general son diferentes, debido a la diferencia de sus costos y a que la política óptima individual para el proveedor no se corresponde con la política óptima individual para el comprador (Heizer y Render, 2009; Díaz y Pérez, 2012).
Luego, si la política que prevalece entre el proveedor y el comprador es "no colaborativa", cada uno de ellos trata de imponer el tamaño de lote que más le conviene, de manera que se establece entonces una relación negativa de ganar-perder entre ambas entidades.
Pero si la política adoptada por estas es colaborativa, como puede ser el caso en la mayoría de las entidades en Cuba, entonces es posible calcular un valor de lote óptimo conjunto que minimice el costo total para ambas entidades.
El análisis colaborativo en la teoría de inventario
En el caso colaborativo, de lo que se trata es de establecer estrategias en el manejo de los niveles de inventario entre comprador-proveedor, de forma tal que el costo total y las órdenes de compra y/o producción sean óptimas al ser analizadas de conjunto por los miembros de la cadena; así el costo total anual conjunto para el proveedor y el comprador se corresponde con la expresión 11:
La expresión 12 es la utilizada para el lote óptimo conjunto:
Modelización cuantitativa e ilustración numérica del método colaborativo en el manejo de los inventarios
Se ilustran los resultados en un ejemplo numérico para su comprobación y se utilizan los valores de los parámetros y de los costos (Tabla 1), como base del caso. En la Tabla 2 se muestran los resultados calculados con las expresiones de la 1 a la 12, de los costos anuales sin considerar los costos de producción (DCP) o de compra (DCC), que son constantes y no influyen en la optimización.
Como puede apreciarse en la Tabla 2, la actividad colaborativa conjunta produce un menor costo total anual que las no colaborativas (el ejemplo solo maneja un producto), lo que indica la conveniencia del trabajo colaborativo entre las empresas de la cadena de suministros.
Por otro lado, si se considera que una cadena de abastecimientos turísticos por lo general la forman más de dos intermediarios, lo que hace al modelo colaborativo más importante en la gestión de inventarios para estas cadenas, ¿cómo se verían los resultados en este caso?
Si se agrega entre las dos empresas del primer caso un mayorista encargado de comprar a la segunda empresa para vender a la primera, la cual opera con los datos de la Tabla 1, se obtienen como cálculos los resultados que se muestran en la Tabla 3, donde se denota aún más la importancia de la colaboración entre empresas de una cadena de suministros.
Este resultado es de interés para las organizaciones cubanas, dado que la estructura y el nivel de subordinación de varias entidades al mismo ministerio u organización empresarial, como el turístico, pudiera y debiera facilitar el trabajo colaborativo interempresarial en materia de optimización de los niveles de inventario.
Análisis colaborativo con enfoque justo a tiempo
Los sistemas JIT son un método de resolución continua y forzada de problemas mediante un enfoque en la reducción del tiempo de producción y del inventario; así, el JIT proporciona una estrategia poderosa para mejorar las operaciones. Con JIT, los materiales llegan donde se necesitan sólo cuando se requieren. Cuando no llegan buenas unidades justo como se necesitan, se identifica un "problema". Al eliminar de esta manera el desperdicio y el retraso, JIT reduce los costos asociados con el inventario excesivo, reduce la variabilidad y el desperdicio, y mejora el tiempo de producción. El JIT es un ingrediente clave en el manejo de bajos niveles de inventario y resulta particularmente útil cuando se desea apoyar estrategias de respuesta rápida y bajo costo (Gilbert, 1994; Fazel, 1997; Chase et al., 2009; Heizer y Render, 2009).
Por otro lado, asesores de la industria de la producción y los servicios acuñaron la frase cadena de valor para referirse al énfasis en que cada paso del proceso de la cadena de suministro que lleva productos o servicios a los clientes, debe generar un valor. Si un paso no genera valor debe suprimirse del proceso (Heizer y Render, 2009).
Estos sistemas se implementan en su conjunto como estrategia general de las organizaciones empresariales, ayudan a mantener la ventaja competitiva y resultan en mayores rendimientos globales para la cadena de suministros mediante la creación de sociedades. Una sociedad JIT existe cuando un proveedor y un comprador trabajan juntos con una comunicación abierta y con la meta de reducir el desperdicio y bajar los costos. Las relaciones cercanas y confiables son cruciales para el éxito del JIT (Kim, Hong y Chang 2006; Chase et al., 2009; Heizer y Render, 2009; Shah et al. 2014).
Diversos estudios realizados en estos temas se han enfocado en los aspectos cualitativos del establecimiento de las relaciones proveedor-comprador que incluyen suministros JIT en una cadena de suministros (Newman, 1988), pero han sido menos los que se han dedicado a modelos cuantitativos e investigaciones en esta área. Pan y Liao (1989) desarrollaron un modelo EOQ para un sistema de suministro JIT. Posteriormente Kelle y Miller (1998) aplicaron herramientas cuantitativas a la negociación proveedor-comprador en un entorno JIT. Más recientemente Díaz y Pérez (2012) y Shah et al. (2014) aplican estos trabajos en la optimización de los inventarios de una cadena de suministros con un enfoque colaborativo entre las empresas de la cadena en entornos de esbeltez y entregas JIT.
Este último enfoque parte de que en un entorno justo a tiempo el comprador requiere recibir envíos pequeños y frecuentes, lo que resulta en mantener bajos costos de inventario. Pero dicho requerimiento puede incrementar los costos del proveedor; entonces resulta conveniente una relación colaborativa (Díaz y Pérez, 2012).
En su investigación Kelle et al. (2003) aportan soporte cuantitativo al cálculo de los tamaños de lote óptimo para el trabajo colaborativo entre proveedor y comprador. A continuación se describen dichos resultados, los cuales fueron utilizados por Díaz y Pérez (2012):
En el análisis planteado se tiene que el tamaño del pedido QC requerido por el comprador debe ser entregado en n envíos de tamaño q (q = QC/n); entonces el proveedor puede producir o adquirir (según sea una empresa manufacturera o un intermediario de venta al por mayor) un pedido de tamaño QP que resulte un múltiplo de q, o sea, QP = mq.
Según los autores, la solución del problema consiste en encontrar los valores óptimos de q, m y n; por lo que, tomando en este caso la misma notación utilizada anteriormente -en la que se han de incluir los términos ZC y ZP correspondientes a costos fijos respectivos de recibir por el comprador y enviar por el proveedor los pedidos de tamaño q-, se tiene que el costo anual para cada uno de ellos es el indicado en las expresiones 13 y 14 (Kelle et al. 2003; Kim et al. 2006; Díaz y Pérez, 2012; Lin y Lin, 2015):
Bajo estas consideraciones de costo, el costo anual total correspondiente al más pequeño es el del comprador. Esta mejora es marginalmente decreciente con el aumento de QC y las desventajas de esta cantidad muy grande contratada compensarán la mejora en el costo. Esta desventaja no se cuantifica en los modelos anteriores; sin embargo, la pérdida de flexibilidad y las preocupaciones de los cambios de producto y compromisos a largo plazo pueden resultar en un alto riesgo de que estos puedan ser mayores que el ahorro anual sobre el costo de ordenar. Para cuantificar el riesgo, se introduce un nuevo parámetro de costo que representará la preocupación empresarial de tener una cantidad de pedido muy grande (Kelle et al., 2003).
El nuevo parámetro de costo, denotado por LC; representa la tasa del costo de perder la flexibilidad por unidad de la cantidad en unidades monetarias contraída pero aún no recibida, de lo que se obtiene la expresión 15:
Luego, al suavizar los requerimientos de integridad para los valores de m y n, hallando las derivadas parciales de la función xJ(m,n) y J(m,n) propuesta por Kelle et al. (2003) con respecto a m y n e igualándolas ambas a 0; se deducen las expresiones para los valores óptimos de m y n. Este proceso permite encontrar los valores óptimos m*, n* y qJ*.
Principales resultados
Con la utilización del mismo caso de la sección anterior y la adición de los valores ZC = $0,8 por envío y ZP = $3,6 por envío, es posible calcular los valores óptimos de n*, m* y qJ*, con el empleo de las expresiones de la 12 a la 15 y las ofrecidas por Kelle et al. (2003). El proceso de cálculo para este sistema colaborativo con enfoque JIT y operaciones esbeltas es algo complejo, pues para determinar n*, m*, QC* y qJ* se necesita realizar varias iteraciones en busca de la combinación de valores que minimicen el costo total conjunto óptimo (CTAJ*) para las empresas que integran la cadena de suministros.
Ilustrando los cálculos, al seguir el ejemplo de la sección anterior, se obtienen los siguientes valores:
• n* = 80 envíos por cada orden emitida por el comprador.
• m* = 12 envíos por cada lote producido por el proveedor.
• qJ* = 125 unidades en cada envío del proveedor al comprador.
• QC* = 10 000 unidades es el tamaño óptimo de la orden del comprador.
• QP* = 1 500 unidades es el tamaño óptimo del lote a producir por el proveedor.
• CTAC = $ 339 al año, es el costo total anual para el comprador.
• CTAP = $ 1 171 al año, es el costo total anual para el proveedor.
• CTAJ = $1 510 al año, es el costo de la operación conjunta entre proveedor y el comprador.
Si se realizan los cálculos para el caso en que m = n = 1, es decir, QC =QP =qJ*; que sería en el caso en que se realice un solo envío de magnitud igual al tamaño de la orden del comprador, es también igual el tamaño del lote a producir por el proveedor. Los resultados obtenidos serían los siguientes:
• qJ* = QC* = QP* = 1 400 unidades en cada envío del proveedor al comprador.
• CTAC = $2 477 al año, es el costo total anual para el comprador.
• CTAP = $602 al año, es el costo total anual para el proveedor.
• JCAJ = $3 079 al año, es el costo de la operación conjunta entre proveedor y el comprador.
Como se puede apreciar, el costo de esta última variante que resulta operativamente más sencilla, y además coincide con la que aplican las empresas cubanas en su operación anual es de $3 079 al año, muy superior a la variante óptima obtenida de $1 510 al año mediante un análisis colaborativo con un enfoque JIT y operaciones esbeltas. Esto confirma la utilidad de la colaboración en términos de manejo de inventarios en una cadena de suministros. En la Tabla 4 se comparan los resultados entre el método colaborativo y el método con un enfoque JIT.
Como se explica anteriormente, la actividad colaborativa entre varias empresas produce un menor costo total anual que las actividades realizadas de forma individual por cada empresa dentro de una cadena de suministros. Sin embargo, el óptimo global pudiera perjudicar los intereses individuales de alguno de los miembros de la cadena; pero donde sin lugar a dudas mejoran las relaciones entre las empresas que conforman esta en términos de reducción de desperdicios y optimización en la operación de los procesos, representando altos beneficios para el consumidor final.
Es entonces que se requiere un proceso de negociación entre las diferentes empresas que no pertenezcan a una misma organización o ministerio para acordar los valores de n*, m* y qJ* más convenientes, en cuyos casos el análisis realizado en este trabajo permitiría evaluar distintas alternativas y calcular posibles compensaciones entre las partes, como vía para el establecimiento de acuerdos comerciales justos y en el que siempre primen las necesidades del consumidor final.
Teniendo en cuenta el análisis aquí realizado, sería acertado exhortar la gestión del entorno empresarial cubano en forma de cadenas de suministro con enfoque colaborativo, para superar el marco estrecho de las decisiones óptimas individuales de cada empresa y trabajar hacia la obtención de los beneficios del enfoque colaborativo antes descrito.
La gestión de cadenas de suministros entre empresas de diferentes organizaciones podría ser fácilmente adoptada por el sistema empresarial cubano, dado que la estructura y el nivel de subordinación vigente en el país pudiera y debiera facilitar el trabajo colaborativo, aún más cuando este representa la posibilidad de reducir los niveles de inventario, los desperdicios y trabajar con un enfoque de mejora continua, mediante la optimización de los procesos productivos y de servicios.
CONCLUSIONES
El análisis cuantitativo de los problemas de inventario ha probado ser una potente herramienta para la toma de decisiones acerca de las variables principales que definen el costo y comportamiento de los inventarios; y más cuando se trata de reducir sus niveles de manejo.
En este sentido, el análisis colaborativo en los problemas de inventario en las cadenas de suministro ha venido a sustituir el análisis que tradicionalmente realizan las organizaciones, de manera que se sustituyen las políticas tradicionales por las de ganar-ganar con un enfoque dirigido a la satisfacción del consumidor final del producto.
El análisis colaborativo aquí descrito y su enfoque justo a tiempo, constituyen herramientas que pueden utilizar las empresas cubanas que integran o gestionan cadenas de suministros en las que están involucradas varias empresas del mismo ministerio u organizaciones, siendo posible superar en estos casos el marco estrecho de las decisiones óptimas individuales que no se corresponden con el óptimo de la cadena de suministro en su conjunto, de manera que se extiendan los beneficios económicos de las empresas, así como se eleven los niveles de satisfacción de los consumidores al garantizar altos niveles de disponibilidad de los productos en el servicio que se presta.
Por otra parte, si las entidades del eslabón proveedor-comprador que componen la cadena de suministros no perteneciesen a la misma organización o ministerio, entonces sería necesaria una negociación, en cuyo caso el análisis realizado en este trabajo permitiría evaluar distintas alternativas y calcular posibles compensaciones entre las partes, como vía para el establecimiento de acuerdos comerciales justos y en el que siempre primen las necesidades del consumidor final.
REFERENCIAS
ACEVEDO, J. A. (2010). La logística moderna en la empresa. La Habana: Ed. Félix Varela.
AIELLO, J. L. (2008). Rightsizing Inventory. New York: Auerbach Publications.
BALLOU, R. H. (2004). Logística, Administración de la cadena de suministro. México Prentice-Hall.
BANERJEE, A. y KIM, L. (1995). An Integrated JIT Inventory Model. International Journal of Operations & Production Management, 15(9), 237-243.
BOWERSOX, D. J. (2007). Administración y logística de la cadena de suministros. México: McGraw-Hill.
CHASE, B., JACOBS, R. y AQUILANO, J. (2009). Administración de operaciones. Producción y cadena de suministros (12ma. ed.). México, D.F.: McGraw-Hill/Interamericana Editores, S.A. de C.V.
DE VRIES, J. (2007). Diagnosing Management Systems: An Empirical Evaluation of a Conceptual Approach. International Journal of Production Economics, 108(1-2), 63-73.
DÍAZ, J. A. y PÉREZ, D. (2012). Optimización de los niveles de inventario en una cadena de suministro. Ingeniería Industrial, XXXIII(2), 126-132.
FAZEL, F. (1997). A Comparative Analysis of Inventory Costs of JIT and EOQ Purchasing. International Journal of Physical Distribution & Logistics Management, 27(8), 496-504.
GILBERT, F.W., YOUNG, J.A. y O'NEAL, C.R. (1994). Buyer-Seller Relationships in Just-in-Time Purchasing Environments. Journal of Business Research, s.v.(29), 111-120.
GOYAL, S. K. (1988). A Joint Economic-Lot-Size Model for Purchaser and Vendor: A Comment. Decision Science, s.v.(19), 236-241.
HEIZER, J. y RENDER, B. (2009). Principios de administración de operaciones (7ma. ed.). México: Pearson Educación.
HILLIER, F. y LIEBERMAN, G. (2010). Introducción a la Investigación de operaciones (9na. ed.). México: McGraw-Hill, Interamericana Editores, S.A. de C.V.
KELLE, P., AL-KHATEEB, F., & MILLER, P. A. (2003). Partnership and negotiation support by joint optimal ordering/setup policies for JIT. International Journal of Production Economics, 81(s.n.), 431-441.
KELLE, P. y MILLER, P. A. (1998). Quantitative Support for Buyer-Supplier Negotiation in JIT Purchasing. International Journal of Purchasing and Materials Management, 34(2), 25-30.
KIM, T., HONG, Y., & CHANG, S. Y. (2006). Joint economic procurement-production-delivery policy for multiple items in a single-manufacturer, multiple-retailer system. International Journal of Production Economics, 103(1), 199-208.
LIN, Y. J y LIN, H. J. (2015).Integrated Supply Chain Model with Price-dependent Demand and Product recovery. Journal of Applied Science and Engineering, Vol. 18, No. 3, pp. 213.
LOPES, I., GÓMEZ, M. I. y ACEVEDO, J.A. (2012). Situación de la gestión de inventarios en Cuba. Ingeniería Industrial, XXXIII (3, septiembre-diciembre), 317-330.
MUCKSTADT, J. A. y SAPRA, A. (2010). Principles of Inventory Management. When You Are Down to Four, Order More. Springer Series in Operations Research and Financial Engineering. London: Springer Science.
NEWMAN, R. G. (1988).The Buyer-Supplier Relationship Under Just-in-Time. Production and Inventory Management, 29(3), 45-49.
PAN, A. C., LIAO, C. J. (1989), "An Inventory Model under Just-in Time Purchasing Agreements". Production and Inventory Management Journal. Vol. 30 No. 1, pp. 49-52.
RUSHTON, A., CROUCHER, P. y BAKER, P. (2010). The Handbook of Logistics & Distribution Management (4ta. ed.). India: Replika Press Pvt Ltd.
SCHROEDER, R.G. (2005). Administración de operaciones (3ra. ed). EE.UU: McGraw-Hill.
SHAH, N. H., PATEL, D. G. y SHAH, D. B. (2014). Optimal Integrated Inventory Policy for Stock-Dependent Demand when Trade Credit is Linked to Order Quantity. Investigación Operacional, 35(2), 130-140.
TAHA, H. (2012). Investigación de operaciones (9na. ed.). México: Pearson Educación.
WILD, T. (2002). Best Practice in Inventory Management (2da. ed). Gran Bretaña: Elsevier Science Ltd.
Recibido: 03/06/16
Aprobado: 09/03/17
Aliosky Camacho Rodríguez. Departamento de Turismo de la Facultad de Ciencias Económicas, Universidad Central Marta Abreu de Las Villas, Santa Clara, Villa Clara. acamacho@uclv.edu.cu













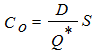 (1)
(1) (2)
(2)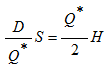 (3)
(3)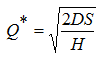 (4)
(4) (5)
(5)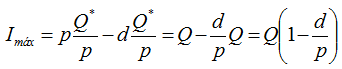 (7)
(7)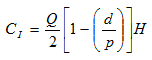 (8)
(8) (9)
(9)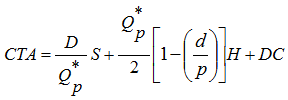 (10)
(10)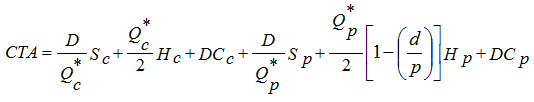 (11)
(11) (12)
(12) (13)
(13) (14)
(14)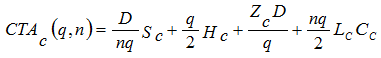 (15)
(15)
