Artículo original

Modelo de predicción de series temporales para la demanda turística de la Cadena Hotelera Cubanacán

Modelo de previsão das séries temporais para a procura turística da Cadeia de Hotéis Cubanacán

0000-0003-1974-9209Reinier Fernández López^{1  *}  , 0000-0002-8923-764XLedy Raúl Díaz González¹  , 0000-0002-4885-5337Juan Carlos Alfonso Alemán²  , 0000-0001-9256-2980Olga Barrio Padrón³ 

¹ Universidad de Pinar del Río "Hermanos Saíz Montes de Oca". Facultad de Ciencias Técnicas. Departamento de Matemática. Pinar del Río, Cuba.

² Fondo Cubano de Bienes Culturales. Pinar del Río, Cuba.

³ Delegación Provincial del Ministerio de Turismo. Pinar del Río, Cuba.

RESUMEN

La demanda turística influye de manera vital en la planificación y proyección de los decisores en esta actividad. En tal sentido, pronosticar la demanda turística, integrando de este modo las cadenas productivas al resto de las actividades socioeconómicas de los procesos de producción y servicios, se convierte en una herramienta insoslayable. El presente trabajo tiene como objetivo elaborar un modelo de pronóstico para la demanda turística mediante el empleo de técnicas de series temporales, que permita predecir el comportamiento del turismo, sustentado en la metodología Box-Jenkins y que respalde el proceso de toma de decisiones en la Cadena Hotelera Cubanacán de Pinar del Río, Cuba. Se logró formular un modelo riguroso con la utilización de los métodos estadísticos-matemáticos como ejes rectores de la investigación, además, se modeló la demanda turística hasta diciembre de 2019.

Palabras-clave: demanda; metodología Box-Jenkins; series temporales; turismo

RESUMO

A procura turística tem uma influência vital no planeamento e projeção dos decisores nesta atividade. Neste sentido, a previsão da procura turística, integrando assim as cadeias produtivas com o resto das atividades socioeconómicas dos processos de produção e de serviço, torna-se uma ferramenta inevitável. O objetivo deste documento é desenvolver um modelo de previsão da procura turística utilizando técnicas de séries temporais, que permite a previsão do comportamento turístico, baseado na metodologia Box-Jenkins e que apoia o processo de tomada de decisão na Cadeia de Hotéis Cubanacán em Pinar del Río, Cuba. Um modelo rigoroso foi formulado utilizando métodos estatísticos-matemáticos como princípios orientadores da investigação. Além disso, a procura turística foi modelada até dezembro de 2019.

Palavras-Chave: procura; metodologia Box-Jenkins; séries temporais; turismo

Introducción

Una planificación deficiente del turismo implica una mala gestión que, sin dudas, degrada esta actividad. Los destinos de todo el mundo se ven beneficiados cuando se gestiona correctamente este sector, a partir de una planificación adecuada ^{(Hącia, 2019)}. El efecto integrador que abarca a casi todos los sectores de la economía convierten al turismo en una de las industrias más diversas del mundo ^{(Meschede, 2020)}.

Son innumerables sus efectos de orden social y también puede ser visto como una actividad económica por elementos definitorios. Es por ello que el sector turístico debe ser capaz de comprender la demanda y cómo se distribuirá a lo largo del tiempo ^{(Feng et al., 2019)}.

En tal sentido, la demanda de un destino se convierte en objeto de estudio de suma importancia: conocer las características de los viajeros, a qué segmento pertenecen, el gasto turístico, los niveles de satisfacción, entre otros. El análisis de los rasgos distintivos de la demanda turística conlleva a diseñar las acciones para que el destino sea capaz de satisfacer las necesidades y deseos del turista ^{(Chenguang Wu et al., 2017)}.

Centrarse en el pronóstico a largo plazo (mensual, trimestral y anual) de áreas relativamente grandes (provincias, países y regiones) permite la estimación y el análisis de la demanda futura para un producto en particular, un componente o un servicio a través de diferentes técnicas de previsión. El pronóstico de la demanda futura es central en cualquier actividad de planificación y de operaciones, en particular, en actividades relacionadas con la logística y con la cadena de suministro.

Es evidente la pertinencia de pronosticar para planear el sistema productivo, el abastecimiento y los despachos, de manera que la cadena de suministros opere correctamente. Estas herramientas permiten la obtención de información relevante, precisa y confiable; entonces, es necesario que las empresas utilicen correctamente los modelos y procedimientos más adecuados para tal fin ^{(C. Li et al., 2020)}.

A nivel organizacional, el pronóstico de la demanda es un insumo esencial para cualquier decisión en las distintas áreas funcionales: ventas, producción, compras, finanzas y contabilidad. Los pronósticos también son necesarios en los planes de distribución y aprovisionamientos. La importancia de un pronóstico con escaso margen de error es fundamental para la eficiencia y la eficacia. Esto ha sido en gran parte reconocido por diversos autores ^{(Shaowen Li et al., 2018)}.

Enmarcado en este contexto, se encuentran los antecedentes de las primeras investigaciones respecto a los pronósticos de la demanda turística en Cuba, las cuales no son numerosas, pero las existentes contienen un alto grado de novedad práctica y científica. Tal es el caso de pronósticos efectuados por el Centro de Estudios Turísticos de la Universidad de la Habana y por el Instituto Nacional de Investigaciones Económicas del Ministerio de Economía y Planificación de Cuba.

Entre los autores más relevantes que abordan elementos sobre los estudios de la demanda turística en Cuba, se destacan: Figuerola et al. ⁽²⁰⁰⁵⁾, Rigol Madrazo et al. ⁽²⁰⁰⁹⁾, Josefá Barbosa y Parada Gutiérrez ⁽²⁰¹⁰⁾, Rodríguez Betancourt y Estévez Mártir ⁽²⁰¹²⁾, La Serna Gómez ⁽²⁰¹²⁾, Delgado Castro y Martín Fernández ⁽²⁰¹⁴⁾, González Laucirica y Santa Cruz Rodríguez ⁽²⁰¹⁴⁾ y Díaz Pompa et al. ⁽²⁰²⁰⁾.

De manera general, estos investigadores proponen modelos que contemplan, como ventajas, rasgos del pronóstico de la demanda turística a corto y mediano plazo; incluyen factores que pueden modificar el pronóstico de la demanda en el sector turístico, además de segmentar el mercado emisor; pero no abarcan, de manera explícita, los diversos factores que han influido a través del tiempo. Son escasos los modelos matemáticos de fácil manejo, sustentado en herramientas informáticas; los pronósticos de la demanda turística carecen de proyecciones con distintos márgenes de error para un análisis de mayor profundidad o, simplemente, mencionan el pronóstico de la demanda turística como herramienta fundamental para la toma de decisiones sin hacer uso práctico de la misma.

Por lo tanto, la presente investigación plantea como objetivo: elaborar un modelo de pronóstico a largo plazo para la demanda turística, mediante la aplicación de la metodología Box-Jenkins, que permita caracterizar la evolución turística en este sector estratégico para la economía cubana y proyectar pronósticos con distintos niveles de confiabilidad.

Materiales y métodos

Para caracterizar la situación actual de la demanda turística en Pinar del Rio, Cuba, se emplea el análisis documental y la observación científica. Se emplean métodos estadísticos-matemáticos y herramientas como la metodología Box-Jenkins ^{(Box et al., 1970)}. Se emplearon los softwares R 3.6.3 y R Studio 1.2.5033 para el procesamiento de los datos y la información disponible. También fueron utilizados métodos teóricos para reseñar el desarrollo de los actuales procesos de gestión del turismo en Pinar del Río. Para el análisis, se utilizó la serie cantidad de turistas mensuales entre enero del año 2006 y diciembre de 2018.

El pronóstico comienza con la identificación del Proceso Autorregresivo de Integración de Medias Móviles, utilizando las funciones de auto-arima del software R. Con los parámetros estimados, se conforma el modelo que se valida mediante el análisis de los residuos. Los residuos deben de estar incorrelacionados 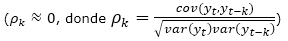para que el modelo sea adecuado. Esto es lo que se conoce como metodología Box-Jenkins ^{(Petrevska, 2017)}.

Modelo Autorregresivo Integrado de Media Móvil

ARIMA es reconocido como uno de los modelos estadísticos de predicción más importantes en las investigaciones sobre los modelos de series de tiempo y creado por Box y Jenkins en 1970. Marcó el comienzo de una nueva generación de herramientas de pronóstico, popularmente conocida como metodología de Box-Jenkins, pero técnicamente conocida como metodología ARIMA.

Está compuesto por dos modelos, el Autorregresivo (AR) y el de Medias Móviles (MA). Tiene parámetros específicos para las series de tiempo: los parámetros p y q, los cuales representan el orden del AR y el orden de la MA, respectivamente. Se adiciona un parámetro d que representa el número de las diferencias ^{(Shuyu Li et al., 2018)}.

El modelo AR se escribe como: y _t = c + a ₁ y _t-1 + … + a _p y _t-p +u _t , donde a ₁ ,a ₂ ,a ₃ ,…,a _p son los parámetros del AR, c es una constante, p es el orden del AR, y u _t es el ruido blanco. Continuamente el modelo MA se puede escribir como: y _t = μ + u _t + m ₁ u _t-1 + … + m _q u _t-q , donde m ₁ ,m ₂ ,m ₃ ,…,m _q son los parámetros de MA, u _t ,u _t-1 ,…,u _t-q son los términos del ruido blanco y μ es lo que se espera de y _t . Integrando estos modelos para obtener el modelo ARIMA, se tiene la expresión siguiente: y _t = c + a ₁ y _t-1 + … + a _p y _t-p + u _t + μ + u _t + m ₁ u _t-1 + … + m _q u _t-q , donde p y q son los términos del proceso autorregresivo y de medias móviles respectivamente.

Modelo Autorregresivo Integrado de Media Móvil Estacional

El Proceso Autorregresivo Integrado de Media Móvil Estacional (SARIMA) es una extensión del ARIMA en el caso de que la serie estacionaria presente el componente estacional, el cual incluye nuevos términos para la diferenciación de orden 12 ^{(Bakar & Rosbi, 2017)}.

Los modelos ARIMA estacionales (P, D, Q) complementan el modelo general no estacional ARIMA (p, d, q), desarrollados para captar los patrones estacionales trimestrales o semestrales presentes en las series temporales ^{(Box et al., 1970)}. La combinación de modelos ARIMA (p, d, q), no estacionales, con ARIMA (P, D, Q) estacionales, conduce al modelo SARIMA (p, d, q)×(P, D, Q), también conocido como ARIMA multiplicativo ^{(López et al., 2017)}. En forma agregada, su representación general es: 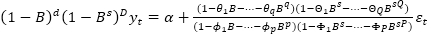donde: d es el número de diferencias regulares, D es el número de diferencias estacionales, s es la amplitud estacional, α constante óptima, q es el número de componentes de medias móviles, Q es el número de componentes de medias móviles estacionales, θ _q son los coeficientes de medias móviles, Θ _Q son los coeficientes de medias móviles estacionales, p es el número de componentes autorregresivos, P es el número de componentes autorregresivos estacionales, Ø _p son coeficientes de los procesos autorregresivos, Φ _p son los coeficientes de los procesos autorregresivos estacionales.

Función de autocorrelación

La función de autocorrelación (ACF) es una herramienta de gran utilidad en la identificación del orden de un modelo de MA. La ACF de un MA_(q) se anula después del retardo q, es decir, ρ _k ≈ 0 para k > q, entonces se tiene que el proceso puede ser modelado mediante un procedimiento de medias móviles de orden q, MA_(q). La ACF representa gráficamente los valores de correlación para k retardos de tiempo ^{(Petrevska, 2017)}.

Dado el supuesto de estacionariedad, donde se tiene var(y _t ) = var(y _t-1 ) la función de autocorrelación se denomina función de autocorrelación parcial (PACF), representa en el gráfico los valores para un desfase k y se implementa para seleccionar el orden del proceso AR. Esta PACF se construye a partir de la expresión siguiente: .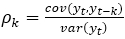

Ambas se utilizan para el análisis de los residuos y para comprobar si el modelo es adecuado o no.

Resultados y discusión

Para cumplimentar el objetivo, se aplicó un análisis univariante de series temporales, con el fin de observar el comportamiento de la serie demanda turística en la Cadena Hotelera Cubanacán, en el periodo comprendido entre enero del año 2006 y diciembre del año 2018. Conviene tener presente que una serie temporal se compone de tendencia, fluctuación cíclica, variación estacional y movimientos irregulares.

Al realizar la representación gráfica de la serie, se puede clasificar como estacionaria, pues la misma oscila alrededor del valor medio histórico de 4364 turistas como se puede apreciar en la figura 1. La prueba Dickey-Fuller, aumentada mediante R, confirma esta clasificación, con un valor de probabilidad de 0.02647, no superando al nivel de significación de 0.05. Cabe recordar que esta tiene como hipótesis alterna que la serie temporal es estacionaria.

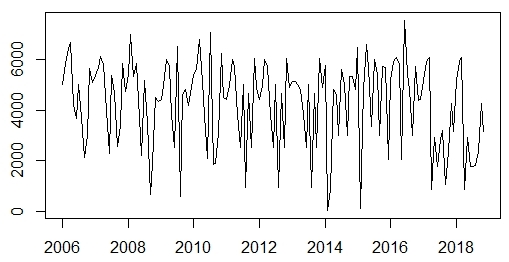Fuente: R, versión 3.6.3

Fig. 1 Serie temporal de la demanda turística mensual (Cadena Hotelera Cubanacán, 2006-2018)  

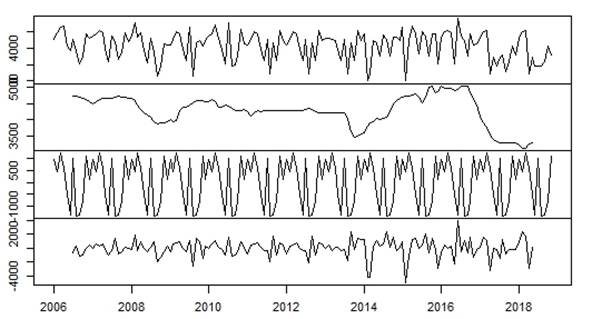
Al descomponer la serie temporal para el análisis de la tendencia y la estacionalidad, se presenta un gráfico que contiene cada componente de la serie, obtenido mediante el método de las medias móviles. En la figura 2, se muestran los valores observados, el componente estacional, la tendencia y los residuos.

Se observan, además, tres fluctuaciones importantes: la primera comienza en el año 2008 a causa de la crisis económica mundial y el azote de los huracanes Gustav e Ike; la segunda se evidencia a partir del año 2013, al entrar en pánico el mundo por el brote pandémico de la enfermedad del Ébola y la tercera, posterior al año 2015, debido a la apertura de las relaciones Cuba-Estados Unidos; no obstante, muestran un decrecimiento a partir del año 2017 como consecuencia del retroceso de estas relaciones.

Fuente: R, versión 3.6.3

Fig. 2 Método de descomposición por medias móviles modelo aditivo para la serie temporal demanda turística (Cadena Hotelera Cubanacán) 

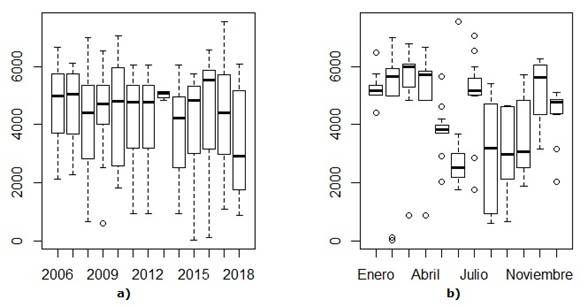
En los gráficos de cajas, se puede apreciar que los años de mayores picos fueron 2006, 2007, 2013 y 2016. En el año 2013, ocurrió la mayor cantidad de visitantes turistas con una baja variabilidad y se corrobora la disminución a partir del año 2017 (Fig. 3a).

Fuente: R, versión 3.6.3

Fig. 3 Gráficos de cajas de la demanda turística por año y por mes (Cadena Hotelera Cubanacán) 

Si se describe la serie por meses, se pueden observar las temporadas que predominan en la cadena hotelera: temporada alta y temporada baja. La temporada alta se concibe a partir de la llegada de los meses de bajas temperaturas en el hemisferio norte (de noviembre a abril) y la temporada baja, los meses más cálidos (de mayo a octubre). Se extrae del gráfico de la figura 3b que los meses de más estabilidad turística son enero y mayo. No ocurre así para los meses, desde agosto hasta noviembre.

La tabla 1 muestra la demanda turística media por años y por meses. Nos permite determinar los años y los meses de mayor y de menor demanda.

Tabla 1 Media para la demanda turística por años y por meses 

Mes	Media		Año	Media	Año	Media
Ene	5171		2006	4699	2018	3456
Feb	4779		2007	4644
Mar	5506		2008	4121
Abr	4950		2009	4419
May	3778		2010	4448
Jun	2902		2011	4287
Jul	5061		2012	4287
Ago	2870		2013	5023
Sep	2936		2014	3798
Oct	3616		2015	4013
Nov	5177		2016	4566
Dic	4383		2017	4292

Fuente: Elaboración propia

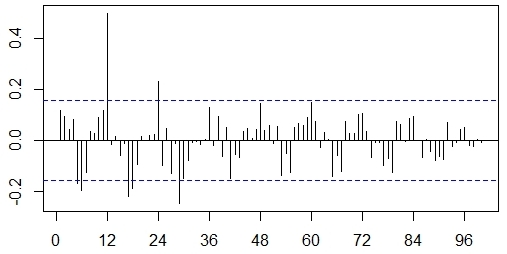
El correlograma de la serie demanda turística en la Cadena Hotelera Cubanacán, que se muestra en la figura 4, permite comprobar que existe un predominio del componente estacional, evidenciado por la presencia de un máximo relativo para el retardo 12; además de estar presente el componente tendencia, pero en menor grado, al ir los valores de la función de autocorrelación de positivos a negativos.

Fuente: R, versión 3.6.3

Fig. 4 Gráfica de la función de autocorrelación para la serie temporal demanda turística (Cadena Hotelera Cubanacán) 

Al detectar estos elementos, a partir de las características de la serie, la opción más recomendable es utilizar los modelos SARIMA. Será necesario realizar una diferenciación de orden doce para eliminar la estacionalidad y, de este modo, lograr una serie puramente estacionaria previa a la aplicación del modelo.

Para la selección del modelo más adecuado, se empleó la función auto-arima de R. A partir de criterios conocidos de predictibilidad, esto es, el criterio de Información de Akaike (AIC), el criterio de Información de Akaike Corregido (AICc) y el criterio de Información Bayesiano (BIC). Además, se emplean las medidas de exactitud como el Error Porcentual Medio (MPE), el Error Porcentual Absoluto Medio (MAPE) y el Error Escaldo Absoluto Medio (MASE). La tabla 2 muestra los resultados que se obtienen a través del software.

Tabla 2 Modelos SARIMA para la serie temporal demanda turística 

Serie demanda turística ARIMA (0.0.0) (1.0.0) [12]
Coeficientes	Sar1	Media
	0.5412	4217.399
s. e	0.0683	226.816
AIC=2697.39	AICc=2697.55	BIC=2706.52
MPE=-138.9312	MAPE=157.0537	MASE=1.064214

Fuente: Elaboración propia

El modelo más adecuado que minimiza todas las medidas de dispersión es un modelo con una diferenciación de orden doce y de orden uno en la parte autorregresiva de la estacionalidad, o sea, un modelo SARIMA (0, 0, 0) (1, 0, 0), con ecuación del modelo .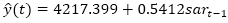

Para validar el modelo, se realiza el contraste de Ljung-Box-Pierce, también conocido como test de portmanteau. La hipótesis nula es que las primeras autocorrelaciones son nulas. El resultado, con un valor de probabilidad igual a 0.1894, implica que las correlaciones son estadísticamente iguales a cero y, por tanto, se puede asumir que los residuos se comportan como ruido blanco.

Esto significa que los residuos estandarizados varían en torno al neutro, sin tendencia, con varianza constante y no hay valores atípicos. Aproximadamente, el 95% de los residuos estandarizados deben estar entre -2 y 2 desviaciones típicas.

El pronóstico de la demanda turística mensual de la Cadena Hotelera Cubanacán para el año 2019 se muestra en la salida de R de la tabla 3. En esta, se observa el pronóstico a través de intervalos para un 80 y un 95% de confianza.

Tabla 3 Pronóstico de la demanda turística para el año 2019 

Mes	Año	Pronóstico	Inf 80	Sup 80	Inf 95	Sup 95
Ene	2019	4740.0	2924.5	6555.0	1963.4	7516.5
Feb	2019	5141.6	3326.1	6957.0	2365.0	7918.1
Mar	2019	5232.5	3417.0	7048.0	2456.0	8009.0
Abr	2019	2406.1	590.7	4221.6	-370.3	5182.7
May	2019	3515.7	1700.2	5331.2	739.2	6292.2
Jun	2019	2880.8	1065.3	4696.3	104.3	5657.3
Jul	2019	2880.8	1065.3	4696.3	104.3	5657.3
Ago	2019	2902.5	1087.0	4717.9	125.9	5679.0
Sep	2019	3203.4	1387.9	5018.9	426.9	5979.9
Oct	2019	4230.7	2415.2	6046.1	1454.1	7007.2
Nov	2019	3644.0	1828.5	5459.4	867.4	6420.5
Dic	2019	3907.0	1842.7	5971.3	749.9	7064.1

Fuente: Elaboración propia

Mediante la función plot de R, se puede obtener la representación gráfica de la serie demanda turística, con su pronóstico para el próximo año como se puede observar en la figura 5.

Fuente: R, versión 3.6.3

Fig. 5 Pronóstico de la demanda turística (Cadena Hotelera Cubanacán, año 2019) 

Con la metodología Box-Jenkins, se obtuvo el modelo matemático de series temporales que posibilitó modelar la demanda turística en la Cadena Hotelera Cubanacán para el año 2019. El pronóstico de la demanda es pertinente, aun si se agregan los datos referidos al estudio acerca de lo que ha trascurrido de 2020. Obviamente, la situación de la pandemia asociada a la COVID-19 va a introducir guarismos heterogéneos, pero que vendrían a ratificar otros procesos externos que no pueden ignorarse.

En el análisis temporal de la serie, se observa el efecto de la crisis económica mundial y el paso de los huracanes Gustav e Ike por el occidente cubano, se evidencia claramente el impacto negativo en el análisis descriptivo de las series temporales en cuestión para la Cadena Hotelera Cubanacán. Es considerable, además, la influencia beneficiosa del acercamiento en cuanto a relaciones diplomáticas entre Cuba y Estados Unidos durante el período de la presidencia de Barack Obama.

Por consiguiente, los modelos matemáticos de series temporales tienen que estar presentes para una planificación de la actividad económica, de forma que se garantice el proceso de proyección y toma de decisiones de las organizaciones. Es probada su efectividad y fácil utilización luego de creada una metodología amigable para el uso de los decisores, que si bien contempla todos los métodos empíricos y estadísticos-matemáticos empleados, con el rigor científico adecuado, también pueda permitirles, a las cadenas hoteleras, llegar a un pronóstico que garantice una interrelación con todo su entorno local e internacional.

Referencias bibliográficas

Bakar, N. A., & Rosbi, S. (2017). Data Clustering using Autoregressive Integrated Moving Average (ARIMA) model for Islamic Country Currency: An Econometrics method for Islamic Financial Engineering. The International Journal of Engineering and Science (IJES), 6(6), 22-31. https://doi.org/10.9790/1813-0606022231

Box, G. E. P., Jenkins, G. M., & Reinsel, G. C. (1970). Time Series Analysis: Forecasting and Control. John Wiley & Sons, Inc. https://books.google.com.cu/books/about/Time_Series_Analysis.html?id=rNt5CgAAQBAJ

Chenguang Wu, D., Song, H., & Shen, S. (2017). New developments in tourism and hotel demand modeling and forecasting. International Journal of Contemporary Hospitality Management, 29(1), 507-529. https://doi.org/10.1108/IJCHM-05-2015-0249

Delgado Castro, A., & Martín Fernández, R. (2014). Pronóstico de la demanda turística hacia Cuba considerando el impacto del cambio climático. Revista Caribeña de Ciencias Sociales. https://www.eumed.net/rev/caribe/2014/08/pronostico-demanda-turistica.html

Díaz Pompa, F., Leyva Fernández, L. de la C., Ortiz Pérez, O. L., & Sierra Mulet, Y. (2020). El turismo rural sostenible en Holguín. Estudio prospectivo panorama 2030. El Periplo Sustentable, (38), 174-193. https://doi.org/10.36677/elperiplo.v0i38.9265

Feng, Y., Li, G., Sun, X., & Li, J. (2019). Forecasting the number of inbound tourists with Google Trends. Procedia Computer Science, 162, 628-633. https://doi.org/10.1016/j.procs.2019.12.032

Figuerola, M., Chirivella, M., & Quintana, R. (2005). Efectos y futuro del turismo en la economía cubana. Centro de Estudios de Economía y Planificación. https://isbn.cloud/9789597166115/efectos-y-futuro-del-turismo-en-la-economia-cubana/

González Laucirica, Á. M., & Santa Cruz Rodríguez, D. (2014). Turismo senior: Análisis del comportamiento de las edades de los clientes que visitan el hotel X. Varadero, Cuba. RES NON VERBA, 4(1), 20-25. http://biblio.ecotec.edu.ec/revista/edicion5/TURISMO%20SENIOR.pdf

Hącia, E. (2019). The role of tourism in the development of the city. Transportation Research Procedia, 39, 104-111. https://doi.org/10.1016/j.trpro.2019.06.012

Josefá Barbosa, A., & Parada Gutiérrez, O. (2010). Propuesta de un procedimiento para el análisis de la demanda turística. TURyDES, 3(7). https://www.eumed.net/rev/turydes/07/bg.htm

La Serna Gómez, A. (2012). El pronóstico de la demanda turística incluyendo variables mercadológicas. TURyDES, 5(12). https://www.eumed.net/rev/turydes/12/asg.html

Li, C., Ge, P., Liu, Z., & Zheng, W. (2020). Forecasting tourist arrivals using denoising and potential factors. Annals of Tourism Research, 83. https://doi.org/10.1016/j.annals.2020.102943

Li, Shaowen, Chen, T., Wang, L., & Ming, C. (2018). Effective tourist volume forecasting supported by PCA and improved BPNN using Baidu index. Tourism Management, 68, 116-126. https://doi.org/10.1016/j.tourman.2018.03.006

Li, Shuyu, Yang, X., & Li, R. (2018). Forecasting China's Coal Power Installed Capacity: A Comparison of MGM, ARIMA, GM-ARIMA, and NMGM Models. Sustainability, 10(2), 506. https://doi.org/10.3390/su10020506

López, A. M., Flores, M. A., & Sánchez, J. I. (2017). Modelos de series temporales aplicados a la predicción del tráfico aeroportuario español de pasajeros: Un enfoque agregado y desagregado. Estudios de Economía Aplicada, 35(2), 395-418. https://doi.org/10.25115/eea.v35i2.2478

Meschede, H. (2020). Analysis on the demand response potential in hotels with varying probabilistic influencing time-series for the Canary Islands. Renewable Energy, 160, 1480-1491. https://doi.org/10.1016/j.renene.2020.06.024

Petrevska, B. (2017). Predicting tourism demand by A.R.I.M.A. models. Economic Research-Ekonomska Istraživanja, 30(1), 939-950. https://doi.org/10.1080/1331677X.2017.1314822

Rigol Madrazo, L. M., Pérez Campdesuñer, R., Noda Hernández, M. E., & González Ferrer, J. (2009). Modelo y procedimiento para la gestión de la demanda turística. Ciencias Holguín, 15(3), 1-12. http://www.ciencias.holguin.cu/index.php/cienciasholguin/article/view/496

Rodríguez Betancourt, R., & Estévez Mártir, M. (2012). Aplicación de la matemática borrosa para la determinación del presupuesto en instalaciones turísticas. Ciencia en su PC, (1), 94-106. https://www.redalyc.org/articulo.oa?id=181324066008

Recibido: 25 de Junio de 2020; Aprobado: 02 de Diciembre de 2020

^*Autor para correspondencia. Correo electrónico: [e-mail]

Los autores declaran no tener conflictos de intereses.

Los autores han participado en la redacción del trabajo y análisis de los documentos.