INTRODUCCIÓN
El análisis de las fuentes bibliográficas constata la existencia de una gran preocupación por el mejoramiento del estudio de la matemática y la formación de su cultura en los profesionales, en especial los de las carreras pedagógicas. La exploración de la práctica educativa permite apreciar que existen insuficiencias en el proceso de enseñanza-aprendizaje y su concreción en la formación de la cultura matemática, manifestadas en los términos siguientes:
Se declara un objetivo referido a la cultura matemática en los estudiantes solo en dos de los documentos normativos sobre las disciplinas específicas de la Licenciatura en Educación Matemática (Álgebra y Análisis Matemático), pero no se precisan orientaciones específicas al respecto.
Existen limitaciones en todas las disciplinas específicas del currículo en la aplicación de vías para formar la cultura matemática de los futuros profesionales de dicha carrera, ya que faltan las precisiones al respecto, tanto en la literatura científica como en la proyección de los programas de las asignaturas.
Se desarrollan aspectos aislados en el proceso de enseñanza-aprendizaje de las disciplinas específicas, como Álgebra, Análisis Matemático, Geometría, Fundamentos Básicos de la Matemática y Probabilidades y Estadística, preferiblemente sobre la historia de la matemática, que contribuyen a la formación de su cultura, pero sin la intención de instrumentarlo en el currículo como parte importante de la formación profesional.
No es referido, por parte de los docentes entrevistados, con precisión y fundamentos sólidos las acciones dirigidas a la adquisición de una cultura matemática en sus estudiantes ni de los aspectos que la constituyen en cada una de las disciplinas del currículo.
No se aprovechan las potencialidades de los contenidos de las disciplinas específicas de la Licenciatura en Educación Matemática para sistematizar los temas culturales, sino que se presentan con un carácter anecdótico y sin las premisas didácticas para llevarlo a cabo.
Aunque los estudiantes manifiestan intereses y motivaciones por el conocimiento de temas atractivos de la matemática, los argumentos sobre elementos que muestren su cultura sobre el tema son escasos y están orientados a la historia de esta ciencia y su aplicación a problemas de la vida.
Por las razones antes mencionadas, el presente trabajo tiene como objetivo ofrecer un modelo didáctico con algunas tareas docentes que contribuyan a la formación de la cultura matemática del futuro profesional.
DESARROLLO
La formación de un profesional de la educación es una tarea importante dentro de cualquier sociedad. El proceso de enseñanza-aprendizaje establece su alcance desde la visión y preparación del docente y esto, a su vez, constituye un objetivo puntual que contribuye a la creación de los futuros profesores. La elaboración de una propuesta didáctica puede ser analizada por un sistema de evaluación confiable que permita determinar la cultura matemática adquirida por los estudiantes en función de su formación integral y su desarrollo profesional.
Uno de los objetivos de los programas de disciplinas debe ir dirigido a la formación de la cultura matemática del futuro profesional. De esta manera, aparecen las asignaturas Análisis Matemático y Álgebra en el Plan de Estudio E de la Licenciatura en Educación Matemática. El Ministerio de Educación (2016) plantea «desarrollar, a través del aprendizaje de esas disciplinas, una cultura matemática y formas de pensar y actuar, sustentadas en la utilización de procesos de pensamiento, métodos, enfoques interdisciplinarios, procedimientos y estrategias, tanto cognitivas como metacognitivas, y una conducta en correspondencia con las principios y normas de la ética profesional pedagógica» (p. 124).
Varios autores han dado una definición de cultura matemática, como son Molina (2003), Program for International Student Assessment / Organización para la Cooperación y Desarrollo Económico (PISA/OECD, 2004), Mingüer y Lezama (2007), Cantoral (2013b) y Sánchez (2015). Estos estudiosos presentan la cultura matemática como actividad, al vincularla a lo práctico y a lo social; además, se refieren, indistintamente, a los aspectos cognitivos y aplicativos de la asignatura, pero no tienen en cuenta de manera directa o implícitamente la cuestión histórica y formativa como elementos que también caracterizan a la cultura matemática.
Por otra parte, para un estudiante de la Licenciatura en Educación Matemática no basta con alcanzar la capacidad de relacionar, identificar, crear, o resolver problemas sociales o personales, sino que también necesita una cultura para solucionar problemas relacionados con su profesión ya que él mismo tendrá que trasmitir en el futuro ese conocimiento a sus estudiantes.
Otros autores han aportado aspectos esenciales que direccionan la actividad del alumo a la formación de la cultura matemática, tales como de Guzmán (1984) León (1999), Anacona (2003), Molina (2003), Camarena (2009), Cantoral (2013a) y Arteaga (2017). Sin embargo, no muestran una vía para formar la cultura matemática de los futuros profesores de las carreras pedagógicas. Estos aspectos son direccionados hacia lo cognitivo, lo histórico de la matemática, su aplicabilidad a diferentes áreas del saber, de la naturaleza y de la vida práctica, pero no de manera sistemática.
La UNESCO (2001) plantea que el concepto de cultura hace alusión al conjunto de rasgos distintivos espirituales y materiales, intelectuales y afectivos que caracterizan a un grupo específico de sujetos. En el caso de la cultura matemática, el concepto es aplicable a los profesionales que realizan actividades relacionadas con dicha ciencia, así como su estudio y enseñanza. Esta cultura se obtiene como resultado de un proceso de asimilación del conocimiento, de la historia, de la aplicabilidad no solo de aspectos didácticos, sino también éticos de la matemática, adquiridos durante la socialización, comunicación y en el accionar consciente y participativo del sujeto en la sociedad.
Según Álvarez (1999), la dimensión es la proyección de un objeto o atributo en una cierta dirección, de ahí que se consideren como dimensiones de la cultura matemática a la cognitiva, la histórica, la de aplicabilidad y la formativa. Estas son definidas de la siguiente manera:
Dimensión cognitiva: se expresa en los contenidos propios de las disciplinas específicas de la carrera y en las alternativas de solución a los problemas profesionales sustentados en la apropiación de los conocimientos, habilidades, valores, la logicidad del pensamiento, el enfoque interdisciplinario.
Dimensión histórica: se expresa en conocimiento sobre la génesis y evolución de los descubrimientos y desarrollo de la ciencia matemática y su enseñanza.
Dimensión de aplicabilidad: se expresa en la actividad práctica que realiza el sujeto con el fin de describir, predecir, prescribir y transformar la realidad en diferentes contextos al utilizar la matemática.
Dimensión formativa: se expresa en los métodos, procedimientos, algoritmos, modos de actuación y valores.
La cultura matemática resulta significativa para un futuro profesional de la enseñanza de la matemática. Autores como de Guzmán (1984), Bishop (1999), Mingüer y Lezama (2007) y Sánchez (2015) se refieren a la formación de la cultura matemática como proceso, destacan la necesidad de formarla desde las clases de dicha asignatura y consideran que, al identificarla en el docente, se podrá tener una idea acerca de su discurso matemático escolar en el aula, pero tienen en cuenta las dimensiones: cognitiva, histórica, de aplicabilidad y formativa en su conjunto, ni proponen vías para su formación, ni hacen referencia al estudiante en formación de la Licenciatura en Educación, Matemática.
Lo anteriormente expuesto, junto a la necesidad de formar una cultura matemática en los futuros profesores y la posibilidad de operar con ella dada las dimensiones que la caracterizan sirvieron de base a la definición que asumen los autores en relación al campo específico de la investigación. Por esta razón, se entiende por formación de la cultura matemática al proceso de adquisición y trasmisión del conjunto de rasgos distintivos espirituales y materiales, intelectuales y afectivos, revelados a partir de las dimensiones cognitiva, histórica, de aplicabilidad y formativa que caracterizan la cultura matemática en función de su profesión en la sociedad.
Es de gran importancia contar con la definición de un modelo para su formación en el proceso de enseñanza-aprendizaje. Varios autores, como Rosental y Iudin (1973), Guétmanova, Panov y Petrov (1991), Ferrer (2000), Pérez et al. (2002), Téllez (2005), Guerra (2008), Sierra (2008), Martínez (2010), de Armas (2011), Pedroso (2011), Romero (2018) y Quero (2018), coinciden al plantear que un modelo es un modo teórico utilizado para operar con un objeto, proceso o fenómeno al emplear un sistema que esté en condiciones de sustituirlo para facilitar su estudio. Un caso particular a tratar en este trabajo es el modelo didáctico.
Al considerar el criterio de de Armas (2011) que plantea que las definiciones deben expresar con claridad suficiente la esencia de su objeto y que es imprescindible precisar un nivel más específico y contextualizar el campo de acción, se asume, como definición de modelo didáctico, la representación teórico-metodológica que reproduce, simplificadamente, la formación de la cultura matemática en los estudiantes de la Licenciatura en Educación Matemática. Además, se toman, como núcleo articulador en el proceso de enseñanza-aprendizaje de una disciplina, las relaciones establecidas entre sus contenidos y las dimensiones que caracterizan dicha cultura.
VALORACIÓN DE LOS EXPERTOS SOBRE EL MODELO DIDÁCTICO PARA LA FORMACIÓN DE LA CULTURA MATEMÁTICA
Con el objetivo de hacer una valoración del modelo didáctico para la formación de la cultura matemática, se sometieron a la consideración del criterio de expertos los componentes del modelo y las recomendaciones para su uso. Uno de los métodos más utilizados que formó parte de las investigaciones en diferentes esferas fue el criterio de profesionales. Fueron considerados para esto los docentes de la Universidad de Cienfuegos, los institutos politécnicos y profesionales jubilados (docentes e investigadores) de la misma ciudad. Se tuvieron en cuenta los criterios de selección, años de experiencia como docentes en la enseñanza de la matemática, título académico, disposición para colaborar en el trabajo dada su creatividad, buena capacidad de análisis, espíritu crítico y autocrítico, y un desempeño profesional destacado.
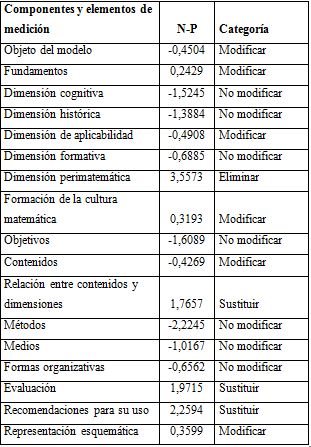
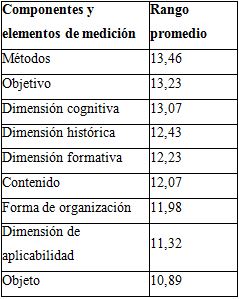
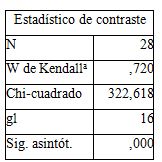
Para la selección de los expertos se tomó una muestra intencional de 36 docentes, con el objetivo de determinar su nivel de competencia. El procesamiento de los resultados llevó a la conclusión de que 30 docentes fueron declarados como expertos. La primera ronda de expertos tuvo como objetivo valorar el modelo didáctico para la formación de la cultura matemática en los estudiantes de la Licenciatura en Educación Matemática. Los resultados se procesaron estadísticamente y se obtuvieron los puntos de corte de las categorías a comparar con cada uno de los valores promedios de las variables valoradas. En el análisis de los componentes del modelo, los expertos señalaron la categoría evaluativa «eliminar» en la dimensión perimatemática y la categoría «sustituir» en la relación entre los contenidos y sus dimensiones, evaluación y recomendaciones para su uso, de manera que estos valores resultaron mayores que el punto de corte de la categoría «no modificar», o sea, N - P < -0,5836 (Tablas 1, 2). Además, mostró el grado de acuerdo entre los expertos, con la prueba no paramétrica del coeficiente de concordancia ω-Kendall, que resultó ser de 72 %, o sea, alto en la escala asumida (Tablas 3, 4).
Tabla 1 Categorías y rango de valoración del modelo didáctico para la formación de la cultura matemática
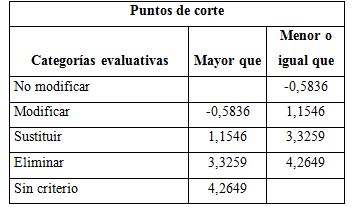
Los expertos refieren que es viable la instrumentación de la propuesta y que, con su aplicación, se puede contribuir a la formación de la cultura matemática en los estudiantes de la Licenciatura en Educación Matemática. Sin embargo, destacaron como deficiencias:
Consideración de la correspondencia del objetivo de la disciplina con los del modelo propuesto.
Insuficiente información para la valoración de las relaciones entre los contenidos y las dimensiones al no concebir ejemplos de tareas docentes a emplear en una disciplina.
Ambigüedades en la determinación de los indicadores para la evaluación de las dimensiones propuestas.
Revisión de las recomendaciones para el uso del modelo didáctico expuesto en correspondencia con el objetivo.
Consideración innecesaria de la dimensión perimatemática, ya que este aspecto se puede incluir en la dimensión de aplicabilidad.
Después del rediseño del modelo didáctico presentado en la primera ronda a los expertos, se realizó una segunda ronda, que expresaba la valoración del modelo y el consenso definitivo hacia las dimensiones cognitiva, histórica, de aplicabilidad y formativa. Se describieron los resultados mediante el análisis de frecuencias absolutas, acumuladas, relativas acumuladas, de la distribución normal inversa. Además, se presentan los puntos de corte de las categorías a comparar con cada uno de los valores promedios de las variables valoradas. La mayor cantidad de encuestados opinaron que los componentes del modelo no debían modificarse. Del análisis de los puntos de corte se infirió que las valoraciones se ubicaran en la clasificación de «no modificar».
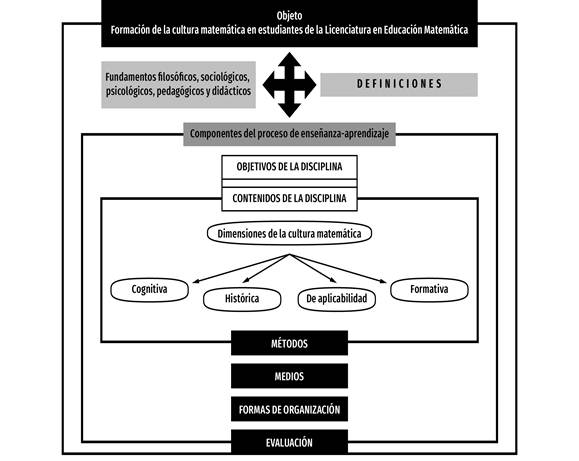
El modelo didáctico propuesto está integrado por los siguientes componentes esenciales: la formación de la cultura matemática en estudiantes de la Licenciatura en Educación Matemática, los fundamentos filosófico, sociológicos, psicológicos y pedagógicos del modelo; el tercero, las categorías declaradas en el modelo, las dimensiones de la cultura matemática, los objetivos y contenidos de la disciplina, así como los métodos, medios, evaluación y formas de organización. Estos elementos coinciden con los del proceso de enseñanza aprendizaje. Para la aplicación del modelo en el proceso de enseñanza-aprendizaje de las disciplinas específicas de la Licenciatura en Educación Matemática se tiene:
Realizar un diagnóstico sobre la cultura matemática que poseen los estudiantes de la Licenciatura en Educación Matemática.
Determinar los objetivos correspondientes a la disciplina a tratar.
Determinar los contenidos de la disciplina en cuestión y su relación con las dimensiones que caracterizan la cultura matemática.
Valorar el uso de literatura no incluida en la bibliografía del currículo.
Incorporar ejercicios que promuevan el conocimiento de la historia de la matemática, la aplicación de esta a otras ciencias y áreas de la vida cotidiana, su relación con situaciones extraescolares y la utilización de los recursos informáticos, lúdicos, audiovisuales y recreativos para su estudio y profundización.
Utilizar herramientas teórico, metodológico y didácticas no solo para establecer la relación de los contenidos de la asignatura a tratar con los aspectos declarados como dimensiones de la cultura matemática, sino también para diseñar las actividades, materiales didácticos y textos escolares.
Una representación esquemática de las relaciones estructurales y funcionales de los componentes del modelo didáctico se establece en la Figura 1.
Dado que el modelo didáctico se materializa en las formas de organización a través de tareas docentes, se muestran, a continuación, ejemplos referidos a la asignatura Análisis Matemático I de dicha disciplina.
Tarea 1 (Tema: El origen de las funciones matemáticas)
Objetivos: Investigar sobre origen y desarrollo de las funciones matemáticas y aplicar a procesos o fenómenos de la vida.
Orientaciones: Elaborar un informe escrito, exponer ordenadamente en clase.
Actividades:
Investigue sobre:
Surgimiento y desarrollo de las funciones matemáticas.
Matemáticos que dieron origen a su estudio.
Ejemplo de curvas que no constituyen funciones.
Importancia de las funciones para la vida.
La existencia en la comunidad de fenómenos y procesos que se puedan modelar al hacer uso de las funciones lineales.
Identifique en cada caso las variables presentes y las relaciones de dependencia existentes entre ellas.
Modele cada proceso o fenómeno utilizando las ecuaciones que correspondan.
Represente gráficamente las funciones auxiliándose del DERIVE.
Bibliografía:
Campistrous et ali (1989) Matemática Décimo Grado. Editorial Pueblo y Educación.
Ochoa, R. (2008). Funciones y temas afines. Tomo I y II. Editorial Pueblo y Educación.
Ribnikov, K. (1987). Historia de las Matemáticas. Mir Moscú
Stewart, J. (2006). Cálculo con trascendentes tempranas. Partes I, II, III y IV. Editorial Félix Varela.
A continuación se observa la estructura de las tareas según los componentes didácticos (Tablas 5 y 6).
Tabla 5 Estructuración de la tarea el origen de las funciones matemáticas, según los componentes didácticos


Tarea 2 (Tema: El acertijo y las sucesiones numéricas)
Objetivo: Aplicar la sucesión de Fibonacci a la solución de acertijos matemáticos, para contribuir a la cultura matemática en correspondencia con la formación cultural y profesional.
Orientaciones: Se realizará de forma independiente y se discutirá en clase.
Actividad:
Acertijo matemático: En una clase sobre sucesiones numéricas el profesor muestra una tabla de 10 columnas con 3 filas, de modo que a partir del primer número de la tercera fila, diagonal ascendente son divisores de 3 y a partir del tercer número de la tercera fila, diagonal ascendente son números primos, formando así dos sucesiones.
Un estudiante pregunta: ¿Qué regularidad establece la diagonal que comienza con el segundo número de la tercera fila? El profesor responde que esta pertenece a una sucesión recurrente estudiada en clases. Le sugiere, además, escribir los términos de las tres sucesiones que aparecen en la tabla y agregar una columna más.
Bibliografía
Sánchez, C. (1982). Análisis Matemático. Tomo I. Editorial Pueblo y Educación.
Stewart, J. (2006). Cálculo con trascendentes tempranas. Partes I, II, III y IV. Editorial Félix Varela.
CONCLUSIONES
Las dimensiones de la cultura matemática para la formación de esta en el proceso de enseñanza-aprendizaje de las disciplinas específicas de la Licenciatura en Educación Matemática se proponen sobre la base del análisis teórico realizado y la valoración dada por los expertos. Se considera que el modelo didáctico materializado en las tareas docentes constituye una vía para la formación de la cultura matemática y para llevar a cabo la misión del profesor de contribuir con la formación cultural del estudiante.