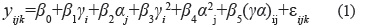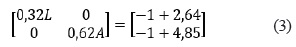Introducción
De acuerdo con Gómez (1972), la unidad experimental (parcela) es el área en la que se lleva a cabo la asignación aleatoria de los tratamientos en un ensayo. Rodríguez et al. (2018) la definen como la unidad de información básica de la experimentación. Esta información, que se convertirá en los resultados del ensayo, proviene de pruebas de naturaleza probabilística y, por lo tanto, está ligada no solo al comportamiento que puede expresar un determinado conjunto de tratamientos, sino que, a otros factores ajenos al mismo, que provocan variabilidad extra y que tienden a opacar el efecto de los tratamientos, llamados en conjunto: error experimental (Montgomery, 2017).
Idealmente, las unidades experimentales deberían ser homogéneas, de modo que después de aplicarles distintos tratamientos se pueda atribuir la diferencia (si existe) exclusivamente al efecto de estos y no debido a otros factores que en conjunto se denominan “ruido”. Sin embargo, conseguir un conjunto de unidades experimentales totalmente homogéneas resulta imposible, particularmente, cuando se realizan ensayos en un campo agrícola, debido a la variabilidad inherente del suelo (Lohmor et al., 2017). La falta de homogeneidad entre las unidades experimentales genera un efecto considerable sobre la magnitud de la variabilidad de los datos no atribuible a causas conocidas (Khan et al., 2017), o sea, sobre el error experimental. Si este error no se controla o se cuantifica, su efecto podría distorsionar la estimación de las medias de los tratamientos y su comparación. Por lo tanto, si se desea que los resultados de un ensayo sean confiables se recomiendan aplicar técnicas experimentales adecuadas, dentro de las que se encuentra, utilizar un tamaño y una forma adecuados de unidad experimental (Condo y Pazmiño, 2015).
La bibliografía especializada señala dos razones de primordial importancia para justificar la necesidad de estimar un tamaño y una forma óptimos de unidad experimental (Rodríguez et al., 1993; Sánchez-Hernández et al., 2006). La primera es reducir el error experimental del ensayo (Guimarães et al., 2019). La segunda se basa en aspectos económicos y prácticos, como ahorro de semilla, espacio, recursos económicos y trabajo. Las parcelas con un tamaño inferior al óptimo pueden dar resultados poco confiables, por otro lado, parcelas grandes pueden incurrir en gastos innecesarios de tiempo y recursos (González et al., 2018). Así pues, la mayor eficiencia de un ensayo se fundamenta en un tamaño y una forma óptimos de unidad experimental (Vallejo y Mendoza, 1992).
Para determinar el tamaño y la forma de parcela existen métodos estadísticos muy variados, la mayoría parten de un ensayo blanco o ensayo de uniformidad (Viloria et al., 2017). Álvarez-Torres et al. (1986) indican que, si bien existen otros métodos, el ensayo blanco es el más preciso, con el inconveniente de que requiere de una inversión considerable de tiempo y recursos. El ensayo blanco es una parcela de extensión relativamente grande que es tratada en toda su superficie uniformemente en cuanto a fertilización, aplicación de agroquímicos y demás labores de cultivo (es decir, no hay aplicación de tratamientos) y que a la hora de la cosecha se subdivide en parcelas pequeñas, llamadas unidades básicas (Schwertner et al., 2015).
Uno de los métodos más utilizados, debido a su eficiencia, es el de regresión múltiple. En este las unidades básicas se agrupan de manera que formen parcelas de diferentes formas y tamaños; a estas parcelas resultantes se les cuantifica el rendimiento correspondiente mediante la adición de los rendimientos de las unidades básicas. Después, para el total de unidades experimentales formadas con una combinación particular se estima la variabilidad residual, medida como coeficiente de variación (CV), que quedará en función de la combinación del largo y del ancho de cada unidad experimental. Esto permite modelar el CV en función del largo y el ancho, lo que genera una superficie de respuesta en tres dimensiones, sobre la cual se puede estudiar los cambios en el CV debido a las variaciones del largo y del ancho y se puede obtener la combinación de estos que hagan que la superficie tenga una curvatura determinada. Usualmente, la curvatura que se busca es cuando la pendiente es -1; debido a que después de este punto añadir una nueva unidad básica en la variable independiente resultará en una reducción de la variable dependiente (CV) menor que la unidad, por lo que el incremento del tamaño ya no justifica la disminución en la variabilidad. Para minimizar la función obtenida con la regresión múltiple se deben calcular las derivadas parciales del coeficiente de variación con respeto al largo y al ancho e igualar ambas a -1, lo que permite encontrar el mínimo deseado. Este método permite encontrar no solo el tamaño, sino también, la forma de parcela que minimice la variabilidad del ensayo (Barrientos-García, 1981; Álvarez-Torres et al., 1986).
El objetivo de este trabajo fue determinar el tamaño y la forma de unidad experimental para ensayos de rendimiento de Brachiaria híbrido CIAT 3608, mediante el método de regresión múltiple, en el cantón de Santa Cruz, Guanacaste, Costa Rica.
Materiales y Métodos
Localización y clima. El ensayo se ejecutó durante los meses de agosto a noviembre del año 2019, en la Finca Experimental de Santa Cruz (N 10° 17’ 6,24’’ y W 85° 35’ 42,95’’), propiedad de la Universidad de Costa Rica, situada en el cantón de Santa Cruz, distrito de Santa Cruz, provincia de Guanacaste, Costa Rica. La misma se encuentra a 54 m s.n.m., laprecipitación promedio es de 1 834 mm/año y la temperatura media anual de 27,9˚C (Cerdas-Ramírez, 2017).
Procedimiento experimental
La siembra se realizó en surcos de 2 cm de profundidad, separados a 0,50 m. El método de siembra empleado fue a chorrillos con una norma de siembra de 5-6 kg/ha de semillas de Brachiaria híbrido CIAT 3608 (Mulato II). El manejo que recibió la parcela fue el mismo en todo lo relativo a fertilización, combate de arvenses, plagas y enfermedades.
Se empleó la técnica del ensayo blanco descrita por Rodríguez et al. (1993). De acuerdo con este método se sembró una parcela de pasto de 12 × 12 m, es decir, de 144 m2. De la cual se dejó dos metros de borde alrededor de todo su perímetro; así se obtuvo un área de 10 × 10 m (100 m2) para ejecutar el ensayo blanco. El suelo del sitio fue clasificado como un Vertic Ustropept. Esta parcela se seleccionó pues representaba las condiciones de la mayoría de la finca en cuanto a topografía y tipo de suelo.
Mediciones de campo. Veinte días después de la siembra se diseñó una cuadrícula sobre la parcela; para esto se emplearon estacas de bambú y cuerdas, de modo que se identificaron claramente las 100 microparcelas (unidades básicas), de 1 m2 cada una. A cada unidad básica se le asignó coordenadas cartesianas, de manera que todas fueran ubicadas e identificadas en el terreno; ambas coordenadas estuvieron dadas por distancias en metros a ejes cartesianos, X fue el ancho e Y el largo de la parcela. La cosecha del forraje se realizó por separado en cada una de las microparcelas a los 100 días posteriores a la siembra. Se cortó a nivel del suelo todas las plantas de pasto procedentes de cada unidad básica y se colocaron en un saco previamente identificado con el número correspondiente a la unidad básica cosechada, según el sistema de coordenadas cartesianas. Con posterioridad, se pesó cada uno de los sacos y se obtuvo el rendimiento en kilogramos.
Análisis estadístico. Con los datos ingresados (producción y coordenadas cartesianas de cada unidad básica) se conformó cada una de las posibles formas y tamaños de unidades experimentales que se obtuvieron por medio de la combinación de las unidades básicas y se calculó el coeficiente de variación (CV) respectivo. Con posterioridad, el CV se modeló en función del largo y el ancho de las unidades experimentales, según la ecuación 1. Se comprobaron los supuestos del modelo con gráficos diagnóstico (cuantiles de los residuos y gráfico de residuos vs predichos).
Donde:
yijk= k-ésimo coeficiente de variación correspondiente al -ésimo largo y al -ésimo ancho.
γi=i-ésimo largo de parcela. Con : 1,…,L.
αj=j-ésimo ancho de parcela. Con : 1,…,A.
(γα)ij= interacción del -ésimo largo con el -ésimo ancho.
εijk= error aleatorio de la k-ésima observación del -ésimo largo y -ésimo ancho
Para cada uno de los coeficientes estimados del modelo de la ecuación 1 se hizo la prueba de hipótesis respectiva para establecer si el valor estimado para cada coeficiente era distinto de cero o no. Cuando el coeficiente estimado no fue significativo (p > 0,05), se excluyó del modelo. Después, se calcularon las derivadas parciales con respecto al largo y al ancho de la función ajustada para el valor predicho del CV y se igualaron a -1. Todos los procedimientos se hicieron con el lenguaje R (R Core Team, 2017).
Resultados
En la segunda columna de la tabla 1 se presenta las estimaciones de cada uno de los coeficientes del modelo y en la quinta columna se encuentra el valor de probabilidad asociado a cada término. Se observa que, a excepción de la interacción, todos los términos son significativos (p < 0,05), por lo que este término se excluyó del modelo de la ecuación 1 y se ajustó el modelo sin interacción. Los resultados se presentan en la tabla 2.
Tabla 1 Coeficientes de regresión estimados y estadísticos asociados para el modelo con interacción.
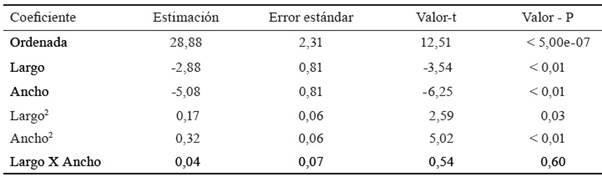
Tabla 2 Coeficientes de regresión estimados y estadísticos asociados para el modelo sin interacción.

Todos los coeficientes estimados del modelo sin interacción fueron significativos (p < 0,05), además, este modelo tuvo un R2 de 0,92; mientras que el modelo con interacción tuvo un R2 de 0,90. Razones por las se seleccionó el modelo sin interacción para realizar las estimaciones.
La función de regresión estimada del coeficiente de variación en función del largo y del ancho se presenta en la ecuación 2.
Después, se calcularon las derivadas parciales con respecto al largo y al ancho de la ecuación 2 y se igualaron a -1, lo que resultó en el siguiente sistema de ecuaciones:
Se resolvió el sistema de la ecuación 3 y se obtuvo la combinación de largo y ancho en la cual se obtiene el punto de curvatura deseado. Esa combinación fue de 5,27 m de largo y 6,16 de ancho; que para efectos prácticos se puede considerar como una unidad experimental de 5 m de largo y 6 m de ancho, correspondiente a un área de 30 m2.
Discusión
El tamaño que se define corresponde al tamaño de parcela útil y no al de parcela total. Por lo que a este tamaño se le deben agregar los bordes que se consideren necesarios, según las condiciones específicas del ensayo.
Se han realizado varias investigaciones relacionadas con las fuentes de error experimental y la aplicación de técnicas para disminuir ese error (Lorentz et al., 2010), donde se menciona que el recurso más práctico y accesible para este fin es el tamaño de la unidad experimental que recibirá el tratamiento. Empero, frecuentemente, se presenta el problema de que la selección del tamaño de unidad experimental a la hora de establecer un ensayo a nivel de campo se hace basado en criterios arbitrarios (Álvarez-Torres et al., 1986; Rodríguez et al., 2018), que no están sustentados con investigación científica. Barrientos-García (1981) y Oliveira et al. (2005) mencionan que la definición del tamaño adecuado de unidad experimental puede estar fundamentado en bases empíricas o en la propia experiencia del investigador y que, si bien estos criterios son más o menos válidos, no pueden sustituir los resultados derivados de los diferentes métodos estadísticos para obtener un tamaño adecuado de unidad experimental, ya que estos son objetivos. Chacín (1977) señala que otro criterio empleado para determinar el tamaño de unidad experimental es la revisión bibliográfica de trabajos realizados en otras localidades, con el inconveniente que el tamaño adecuado de unidad experimental es una característica regional y está afectado por las características agroecológicas de la zona donde se desarrolló el estudio.
Los tamaños reportados en investigaciones publicadas, relacionadas con Mulato II, varían desde los 4 m2 hasta los 1 200 m2; este amplio rango de valores puede generar inconsistencia e incertidumbre en los investigadores que tomen estas investigaciones como guía para determinar el tamaño. Más aún, estos tamaños no han sido validados desde el punto de vista de minimizar el error experimental y, a pesar de la importancia que tiene desarrollar conocimiento desde las condiciones locales, es nula la investigación que se ha realizado en esta área.
Debido a su flexibilidad adaptativa, que le permite presentar un crecimiento eficiente y altas producciones de biomasa de buena calidad, aún en suelos que presentan problemas de acidez y baja fertilidad, la investigación de pastos como el Mulato II para forrajes en el trópico se vuelve promisoria (Villalobos-Villalobos y Montiel-Longhi, 2015). No obstante, en el trópico, el suelo es muy variable en espacios de terreno relativamente pequeños (Asif y Anver, 2003); entonces, la heterogeneidad del suelo siempre va a estar presente en los ensayos realizados en el campo y es una de las principales causas del error experimental.
Para minimizar este error, además de otras estrategias, se debe seleccionar el tamaño y la forma apropiados para la unidad experimental. No obstante, a pesar de que el tamaño y la forma de unidad experimental se reportan como una herramienta valiosa para controlar el error experimental, su estudio ha perdido importancia en los últimos años, lo que se refleja en las escasas referencias bibliográficas de fechas recientes. Ello probablemente, se debe al auge de tecnologías intensivas de cultivo donde grandes áreas son sometidas a los tratamientos. Sin embargo, en países pequeños, donde no existen estos sistemas de producción, donde hay limitantes de terreno y las labores de cultivo aún se realizan manualmente este tipo de investigación pasto puede convertirse en una gran ayuda para los investigadores locales, en aras de maximizar los recursos y obtener resultados confiables (Vargas-Rojas y Navarro-Flores, 2019).
Este trabajo provee información experimental que se puede emplear como herramienta importante cuando se discute acerca del tamaño de unidad experimental para ensayos del pasto Mulato II en zonas agroecológicas similares a las de Santa Cruz, Guanacaste. De esta manera, cualquier técnico o institución encargados de desarrollar investigación con este pueden utilizar los resultados de este trabajo como punto de partida para definir el tamaño de unidad experimental. La importancia de esta información es que es producto de investigación realizada bajo las condiciones locales; entonces utilizar estos resultados para establecer un tamaño adecuado de parcela sería más correcto que recurrir a la revisión de literatura extranjera o a criterios arbitrarios. Cabe mencionar que es importante realizar este tipo de investigación en diferentes zonas agroecológicas, de manera que se pueda estudiar cómo cambia el tamaño de unidad experimental según las condiciones ambientales.