INTRODUCTION
Spallation term refers to nuclear reactions induced by energetic light projectiles, which cause the emission of a large number of hadrons (mostly neutrons) or fragments. The interaction process, can be analyzed as having two different stages. The first one, the intra-nuclear cascade (INC), is a fast direct stage (10−22 s), in which incident particles undergo multiple scatterings within the nucleus, leaving it in an excited state. The second stage, with an approximate duration of (10−16 s) corresponds to the deexcitation of compound nucleus which losses its energy by evaporation of light particles or by fission. The potential applicability of the spallation reactions in the design of the Accelerator Driven System (ADS) reactors has increased the interest on their study. The ability for transmuting the wastes generated in common reactors, a minimum production of long-lived wastes, an extremely high level of inherent safety and more efficient use of abundantly available natural fuel 232Th are the most attractive features for this new type of reactors [1,2]. The spallation module constitutes the physical and functional interface between the sub-critical reactor and the accelerator. Due to the large spectrum of emitted particles, it is complicated to have experimental values of all the involved magnitude over all energy range. As a consequence of the lack of experimental data, transport codes [3] are used for the description of microscopic interactions within the nucleus throughout the reaction process, which complement the study of the spallation reactions.
The IAEA Benchmark of Spallation Models [4] is an available database, which covers all the possible emission channels with ten different targets and more than 40 sets of experimental data for incident projectiles with energies from 20 MeV to 3 GeV. The results of the multiplicity of light particles (n, p, α) obtained with CRISP code were compared with the previously mentioned database. This comparison allowed us to demonstrate the predictive capacity of our code in the light particles emission. This paper is organized as follows: In Section 2 the general characteristics of the CRISP code are presented. Section 3 presents and discusses the results obtained and Section 4 is dedicated to conclusions.
THE CRISP CODE
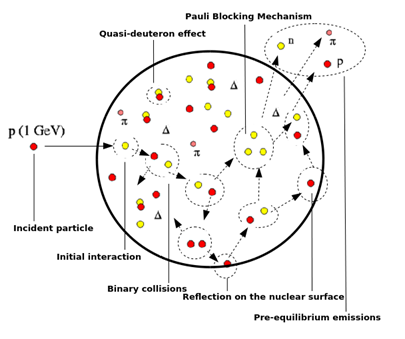
The CRISP code uses an algorithm written in C++ and based on the Monte Carlo method. Although the code has been described in previous contributions it was considered appropriate to emphasize its main features. Two main modules are coupled: The Monte Carlo Multicollision (MCMC) which is used to describe the intra-nuclear cascade and the Monte Carlo Evaporation-Fission (MCEF) [5] an approach to the description of the deexcitation of the compound nucleus through the competitive process of evaporation/fission. Due to the relatively high incident energy, the INC (Figure 1) is considered as a sequence of individual particle events, considering only binary interactions. During the MCMC simulation all the nucleons move simultaneously and the time-ordered sequence of elementary collisions takes into account the probability of interactions between all the particles based on their cross sections. The MCMC also considers that the particles move in a straight line and that the Broglie wavelength is smaller in relation to the effective range of the nuclear interactions. The projectile interacts only with one nucleon of the target nucleus. The binary interaction is not affected by the presence of the other nucleons, it will depend only on binding effects, and on nucleon-nucleon correlations caused by nuclear matter.
Pauli Blocking Mechanism is taken into account by dividing the phase-space into cells, and imposing the condition that each cell can be occupied by at maximum four nucleons (isospin and spin numbers are considered). If there is not vacancy in the specific cell, the interaction is blocked. The use of this method for the Pauli blocking allows to employ the energetic criterion to decide the ending of the intra-nuclear cascade. The system evolves over time increasing the number of particles involved in the multicolisional dynamics. Then, the remaining excitation energy is redistributed among the nucleons in the nucleus in a sequence of elementary collisions, which is called Thermalization. The deexcitation of the nucleus described by the MCEF module involves the evaporation process, where only nucleons and alpha particles can escape of the nuclear environment and/or the fission process, in which two lighter nuclei are formed. When there is not enough energy in the nucleus for emitting particles or when the fission occurs, the evaporation process ends. For an accurate description of the spallation reaction, it is necessary to include all the characteristics concerning spatial and energetic angular distribution, the spallation products and neutron multiplicity [6].
The Multiplicity of particles emitted during the INC (neutrons, protons, or alpha particles) can be calculated using the equation (1). It is important to emphasize, for neutrons and protons the contribution involved both, pre-equilibrium and evaporation processes.
whereN ec is the number of effective cascades and N ep is the number of emitted particles of interest.
RESULTS
Figure 2a shows the total neutron multiplicity that was obtained with the CRISP code for four different target nuclei (184W, 197Au, 208Pb) using a beam of protons with 1500 MeV of energy. The results obtained were compared with experimental data and also with other codes used in the study of nuclear reactions such as: MECC7, Isabel and MCEM95 [7].
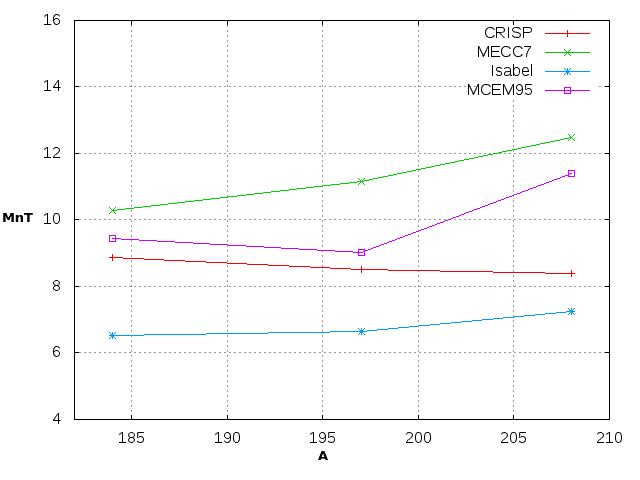
Figure 2a Total neutron multiplicity variation with the increasing of the mass number of the target for a proton incident energy of 1500 MeV.
As it can be observed the total neutron multiplicity is roughly a linear function of the target mass A and increases slowly with the increase of the incident energy of the projectile. It can also be noted that, despite it was obtained an underestimation of the total neutron multiplicity values with the CRISP code the results are much closer to the experimental data than the obtained ones using the other codes. In the case of protons and alphas Figures 2b-2c the lack of experimental data in the energy range studied forced us to compare the results only with other codes such as: CEM95 and Isabel-Pace2 respectively [8].
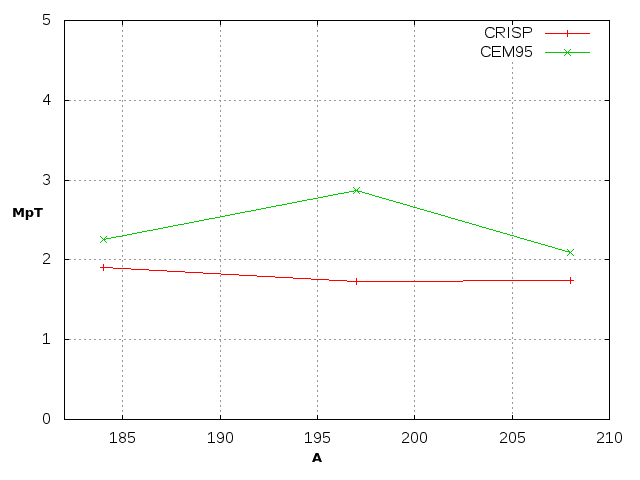
Figure 2b Total proton multiplicity variation with the increasing of the mass number of the target for a proton incident energy of 1500 MeV.
In general, the results obtained with the CRISP code for the total multiplicity of neutrons, protons and alpha particles describe the expected behavior. It is observed the increase of the total neutron multiplicity with the increase of the atomic number of the target and almost a constant behavior in the case of the total multiplicity for protons and alpha particles. However, it is important to do a specific analysis for the results obtained with the doubly-magic nucleus of 208Pb. As it can be seen in Figure 2a the underestimation of neutron production obtained with the CRISP code for this nucleus, which is extremely stable, is higher than for the case of the nuclei of (184W, 197Au).
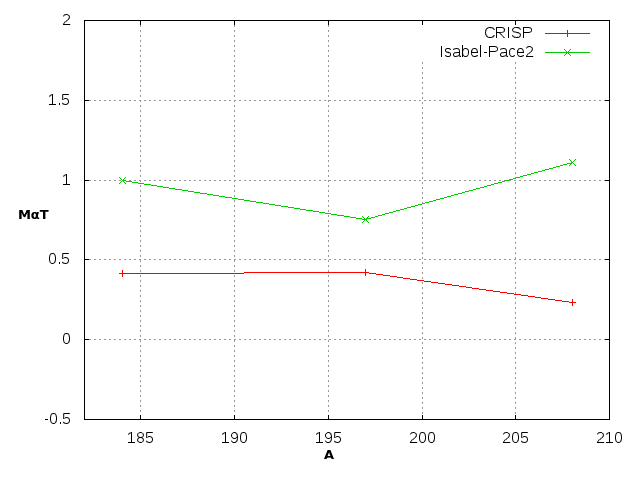
Figure 2c Total alfa multiplicity variation with the increasing of the mass number of the target for a proton incident energy of 1500 MeV.
For the case of the alpha’s multiplicity (Figure 2c), it is also visible that for the nucleus of 208Pb the CRISP code predicts a decrease in the emission of alpha particles while the Isabel-Pace2 predicts an increase. Assuming that the energy of the projectile is evenly distributed among all the nucleons and that no emission of particles occurs, in the nuclei of 184W and 197Au, the nucleons would have more energy and therefore would favor the emission not only of neutrons and protons, but also of alpha particles. In the case of 208Pb , the calculation of the energy needed to separate a neutron, a proton or an alpha particle reveals that the emission of the alpha particle requires approximately 3 times more energy than the emission of nucleons. Due to the energy distributed between all the nucleons, for 208Pb, is lower, it is logical to think that alpha particle emission processes are less favored, which would explain a decrease in their multiplicity. With the aim of deepening in the study of this specific par-par nucleus the comparison of the total neutron multiplicity for the p + 208Pb reaction in the energy range from 800 MeV to 1600 MeV was done. Figure 3 shows the comparison between the CRISPcodeand other 3 codes that are included in the database [4]. After comparing with 15 different models we can affirm that the results obtained by the CRISP code and the results reported by the other codes are in a good concordance.
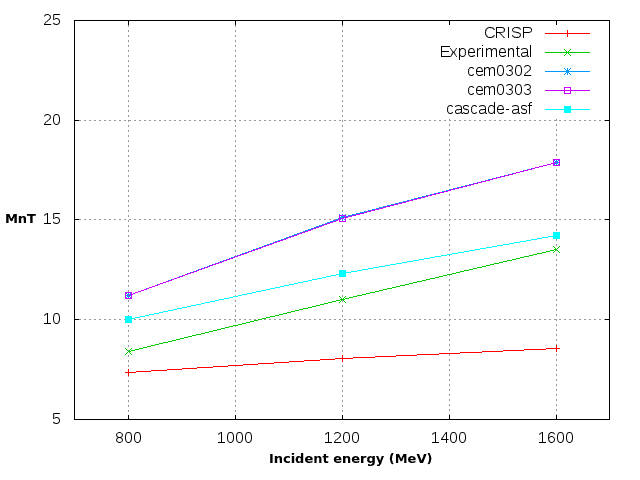
Figure 3 Total neutron multiplicity variation with the increasing of the energy of the projectile. CRISP vs. experimental data vs (cem0302, cem0303, cascade-asf).
It is important to point out that the code was always running with 106 stories for each energy of interest which allows us to achieve a correlation between the time that the code needs and an acceptable statistical variability.
CONCLUSION
The CRISP code represents a good tool to describe the complex characteristics of the nuclear reactions and opens the opportunity for applications in quite different fields, such as spallation and/or fission processes initiated by different projectiles in a wide range of energy. In this work the CRISP code was used to study the multiplicity of neutron, proton and alpha particles with the aim of knowing the general behavior of the code in relation to other codes, which have been already tested. We can conclude that:
(1) In the fast phase of the reaction, neutrons with energy greater than 20 MeV are the ones which have a greater contribution to the multiplicity of neutrons. (2) For different target nuclei (184W, 197Au,208Pb) the total neutron multiplicity increases with the increase of the atomic number of the target and for protons and alpha is approximately constant. (3) For proton reaction in 208Pb, in the energy range from 800 to 1600 MeV, the results obtained with the CRISP code and the results reported by the other codes from the database originated as a result of the IAEA Benchmark of Spallation Models are in a good agreement.
For forthcoming works special attention will be given to the pion production during the INC. Due to the fact that, pions are only produced in the fast phase of the nuclear reaction, their study would allow us to validate the predictive capacity of the MCMC, without requiring the complete description of the nuclear reaction. This would be very important since the results obtained from the ending of the INC in terms of the excitation energy for the residual nuclei are the starting input data from the MCEF.