Introducción
Una de las preocupaciones de los de gobiernos, científicos y del pueblo cubano, en general, es el surgimiento de nuevos brotes de la epidemia una vez que se hayan desescalado las medidas de control de la movilidad y distanciamiento social, que nos ha impuesto esta situación epidémica. Debido al tiempo que han durado estas necesarias medidas para evitar la transmisión de la enfermedad y debido además, a la necesidad de reactivar la economia del país lo más rápido posible una vez que se haya eliminado el virus, existe preocupación por parte de las autoridades de salud pública por el alto número de ciudadanos que han quedado suscestibles de contraer la enfermedad, a pesar de haber cumplido disciplinadamente las indicaciones de permanecer en sus casas o mantenerse bien protegidos. Muchas de estas personas que no han tenido contacto con el virus, pueden tener aguna predisposición a contraerlo en caso de encontarse con una persona enferma asintomática que haya ingresado al país despuès de eliminarse las medidas de aislamiento.
Es nuestro interés y objetivo de este trabajo, demostrar mediante modelos dinámicos y teoría cualitaiva de ecuaciones diferenciales, cómo el número reproductivo básico Ro constituye una métrica que incide en la ocurrencia de estos eventos.
Modelo de tipo SIR con demografía y simulaciones
Los modelos de tipo SIR que se usan para generar las curvas de casos activos que se han difundido a nivel nacional, se basan en modelos epidemiológicos publicados.1,2 En este trabajo se considera un modelo SIR con demografía que incluye además un parámetro que ayuda a medir la efectividad de la intervención del Estado, adaptado a las condiciones de Cuba. Las predicciones de casos activos resultantes ajustan muy bien con los resultados registrados. La selección se basa en que este modelo además de lo anterior, permite estimar la existencia de puntos endémicos y la posibilidad de rebrotes. Se consideraron otros modelos, pero mantuvimos el de tipo SIR como estrategia principal para pronosticar los casos activos, el posible pico y la extensión de la enfermedad.
El sistema de ecuaciones diferenciales considerado1 tiene dos posiciones de equilibrio, una en (1,0) un punto de equilibrio libre y otra posición de equilibrio fuera del punto (1,0), que constituye un punto endémico en el caso de que el número de infectados sea positivo. Cuando surge la posición de equilibrio endémica, el punto de equilibrio (1,0) es inestable y bajos ciertas condiciones,1 el punto endémico (en la simulación [0,7; 0,004 ]), se convierte en un sumidero de los datos simulados y es globalmente estable. Esto significa que los pares de ordenados (S, I) siendo S el números de los susceptibles e I el número de infectados, estarán próximos al punto de endemia, haciendo que la enfermedad perdure en el tiempo con un 0,4 % de casos positivos de la población.
Aunque los resultados que aquí se presentan son solo una simulación para obtener conclusiones de cómo proceder para evitar el surgimiento de rebrotes de la pandemia, no dejan de ser situaciones perfectamente posibles, las cuales han aparecido en diferentes países cuando han desescalado algunas medidas.3) Los datos de los casos infectados y recuperados registrados para realizar las corridas se tomaron del sitio web https://covid19cubadata.github.io
Resultados
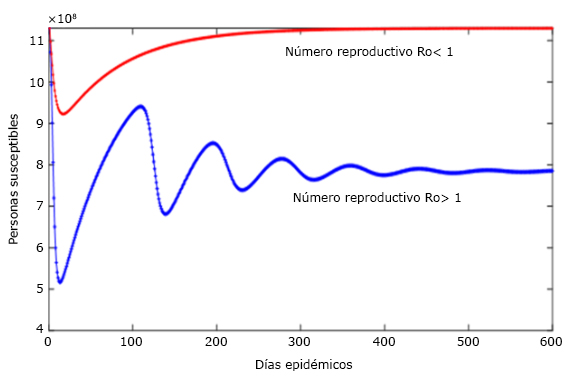
La figura 1 representa la proporción de personas susceptibles contra la proporción de personas infectadas (casos activos). En la simulación se aprecia por el sentido de las flechas, que el movimiento de los pares (S,I) se produce hacia el punto endémico (0,7; 0,004), (es asintóticamente y globalmente estable) lo que significa que se esperaría que el número de susceptibles sea alrededor de unas 12 mil personas susceptibles (Ro*1,13*1e4) y aproximadamente 64 personas enfermas, quizás para fin de año (tiempo tendiendo a infinito).
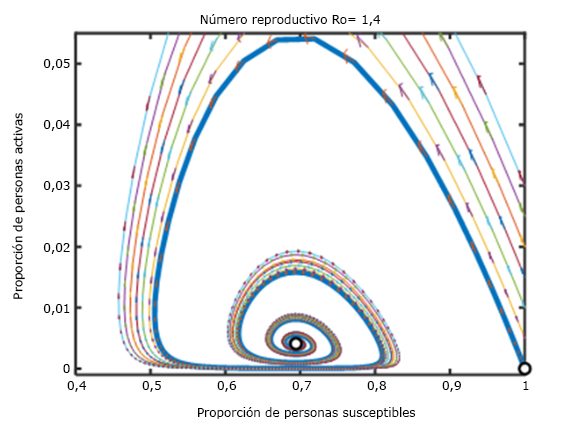
Fig. 1 Las trayectorias se mueven hacìa un punto endémico cuando el número reproductivo básico Ro> 1, lo que origina rebrotes de la epidemia.
El número 0,7 denota que hay un valor muy alto de pobadores que quedan susceptibles a la enfermedad. Si se considera el 70 % del número total de la problación cubana como casos susceptibles tendriamos casi 8 millones de habitantes susceptibles, esta aproximación no es correcta ya que el número de casos confirmados entre la población total de cada país es muy baja, lo que nos lleva a sospechar que solo un porcentaje pequeño de ciudadanos en comparación con el total de la población podría ser susceptibles de contraer este virus, pero quedaria una cantidad no despreciabes de ciudadanos susceptibles al virus, que es lo notorio de este estudio y estos serían la base para el origen de rebrotes.
Algunos países inialmente optaron por la inmunidad de rebaño, esto es, no establecer restricciones a la movilidad y apoyar a las personas más vulnerables, pero al aumentar el número de personas fallecidas, los gobiernos han tenido que dar marcha atrás a esta política. Es necesario destacar que en Cuba nunca se tuvo como opción esta política ya que la vida de todos los ciudadanos tiene mucho valor y el Sistema Nacional de Salud lucha constantemente por salvar a todos.
Los períodos de flutuaciones de las personas susceptibles son independientes del número de la población (Fig. 2). Este parámetro tiene una oscilación amortiguada (los valores propios del sistema tienen parte real negativa y parte imaginaria no nula), la amplitud de los picos de casos activos van siendo menores, hasta estabilizarse con el transcurso del tiempo en una cifra soportable por el sistema de salud. El riesgo de permitir estas fluctuaciones está en las secuelas que deja el virus en los enfermos y en el número de fallecidos que se producen a causa de la enfermedad. Por lo que será necesario que los gobiernos mantengan las medidas epidemiológicas activas durante un largo período hasta que una vacuna pueda aplicarse a la población y esta quede inmunizada.

Fig. 2 La figura ilustra como número de personas susceptibles a la enfermedad oscila con el tiempo cuando R0 >1. El número de casos susceptibles, cuando el número reproductivo es mayor que uno (R0 >1) produce oscilaciones y es lo que facilita que cualquier caso enfermo que se introduzca en la población origine un rebrote (Fig. 3).
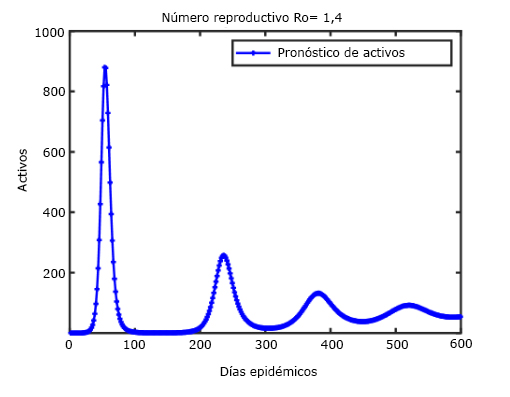
Fig. 3 Control de la pandemia entre los días epidémicos 100-200, se observan los diferentes rebrotes que pueden presentarse si R0 >1.
Se aprecia que una vez controlada la epidemia (intervalo de tiempo entre 100 y 200 días epidémicos) los casos activos podrían nuevamente aparecer en caso que las medidas epidemiológicas se desmantelen y que el número básico reproductivo sobrepase el umbral de 1.
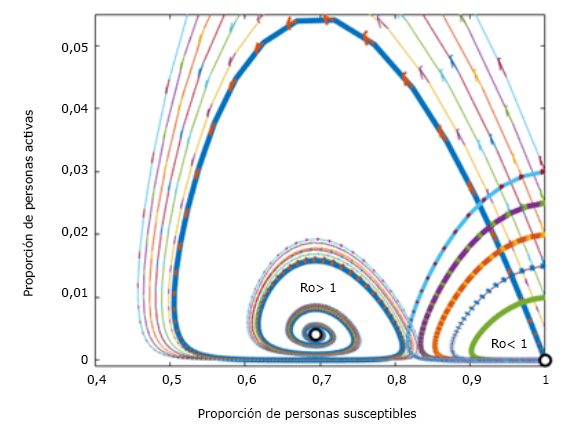
Cuando el número reproductivo básico R0 sea menor que 1, (R0 < 1), el sistema de ecuaciones diferenciales estudiado solo posee un punto de equilibrio en (1,0), este es un punto globalmente estable, por lo que cualquier trayectoria nos lleva a la eliminación total de los casos enfermos y la epidemia desaparece de la nación cubana (Fig. 4).
En el caso de Ro< 1, se observa que no hay oscilaciones en el número de susceptibles a diferencia del caso de Ro> 1
En la figura 5, se muestran los dos puntos de equilibrio del sistema, uno de ellos es endémico en caso de que Ro>1 y para Ro<1 el punto (1,0) es la única posición de equilibrio que aparece, es un punto globalmente estable y conduce a la eliminación total de la epidemia. Para las mismas condiciones iniciales las trayectorias se mueven a posiciones de equilibrio diferentes en cada caso.
Los resultados encontrados demuestran que, desde el punto de vista matemático, se puede dar respuesta a las condiciones que pueden originar un rebrote de la enfermedad.
Consideraciones finales
Consideramos que en Cuba no es poco probable que aparezca un gran rebrote, esto lo avala el trabajo desarrollado por el gobierno y el MINSAP a lo largo y ancho del archipiélago, dando un ejemplo al mundo de la preocupación del gobierno por su pueblo. Esto no significa que no aparezcan nuevos casos confirmados con la COVID-19, ya que una parte importante de la población quedará susceptible y además sabemos que existe una cantidad no despreciable de personas que son asintomáticos pero pueden transmitir la enfermedad.
Nuestro país está previendo un desecalamiento por regiones a partir de cumplimentar un grupo de parámetros, entre los que se encuentra poseer un número reproductivo básico menor que 1. Los casos confirmados que surjan, una vez controlados, conducirán a la eliminación de los riesgos de que la epidemia se expanda y surja un nuevo brote en el país (Fig 5, Ro<1). No obstante, planteamos recomendaciones derivadas de este estudio, que ayudarán a mantener controlados a los casos confirmados que aparezcan.
Recomendaciones
Para lograr que no se produzca un rebrote de la epidemia es necesario:
Mantener el número básico reproductivo por debajo de 1. Lo cual se logra si el número de casos confirmados disminuye lo más posible y se mantiene el control y la vigilancia epidemiológica.
Mantener las pesquisas y visitas a las personas más vulnerables.
Mantener algunos centros de aislamiento que permitan controlar a los contactos de los casos confirmados que surjan o sean introducidos.
Mantener en lo posible el aislamiento físico en escuelas y centros de trabajo, seguir utilizando el teletrabajo como una forma de mantener el distanciamiento y no afectar la economía y los servicios.
Se debe continuar con los programas de prevención que hayan probado su eficacia en este período, como son el lavado de las manos y el uso del nasobuco en centros de trabajo, centros escolares, medios de transporte y de servicios, así como en los domicilios.
Mantener los programas de prevención con vacunas y otros productos farmacéuticos cubanos que han demostrado buenos resultados en la prevención.