ARTÍCULO ORIGINAL

 

Inundaciones pluviales en una cuenca urbana aplicando el método de ponderación mixta

 

Application of mixed weighing method to determine urban flood hazard

 

 

Luis Alejandro Sánchez Román^I , Yoel Martínez González ^II

I Centro de Investigaciones de Recursos Hídricos (CIDRHI) , Universidad Nacional Experimental Francisco de Miranda, Falcón, Venezuela
II Centro de Investigaciones Hidráulicas (CIH), Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba

 

 

 

---

RESUMEN

Los criterios de riesgo por inundaciones pluviales que consideran la acción conjunta de calados y velocidades, en su mayoría han sido desarrollados para cuencas rurales y son aplicados en casos de inundaciones provocadas por desbordamiento de ríos. Con la aparición de los Sistemas de Información Geográfica (SIG) se han desarrollado técnicas para el análisis de riesgo en cuencas urbanas basadas en análisis multi-criterio y en la ponderación de factores combinatorios de distinta naturaleza. Este artículo presenta aportes al método de ponderación mixta para calcular la peligrosidad o amenaza por inundaciones en calles para zonas urbanas, específicamente en la escala de normalización del subíndice (I_Cot) o indicador de propiedades de inundación, construyendo el mapa de peligrosidad en un caso de estudio.

Palabras clave: peligrosidad, riesgo, drenaje urbano, indicador, inundaciones.

---

ABSTRACT

Flood hazard criteria in urban areas, considering combined action of depth and velocity, have been developed for rural basins and are applied in fluvial flooding cases. By using GIS tools and the modules for spatial analysis an analysis of flood risk in urban watershed based on multi-criteria decision analysis and combinatorial weighting factors has been developed. The aim of this paper is to make contributions to the mixed weighing method to determine urban flood hazard. Risk maps were developed in a case study by applying EPA_SWMM model to simulate a 1 hour and 28.8 mm depth rainfall event. Finally, new criteria are proposed for standardization of this indicator by changing the normalized scale, from a qualitative sensitivity analysis and comparing hazard maps.

Keywords: hazard, risk, urban drainage, indicator, floods.

---

 

 

INTRODUCCIÓN

Las metodologías y los criterios utilizados para cuantificar la peligrosidad asociada al flujo en calles es un tema en el cual no existe consenso, por esta razón, es común encontrarse investigaciones donde se construyen mapas de peligrosidad y riesgo pluvial aplicando los mismos criterios que se utilizan en la gestión de inundaciones ocurridas en ambientes rurales. A diferencia de la gestión de inundaciones de origen fluvial (por desbordamiento de ríos), la gestión del drenaje pluvial urbano requiere del conocimiento exhaustivo de la evolución de caudales y profundidades de flujo en las calles y avenidas de la zona urbana (Hauger 2006). La revisión de conceptos realizada para este trabajo, se basa en gran parte en los documentos producidos por el proyecto FLOODsite (Samuels 2006). En general, se recomienda que para cualquier vía el tirante asociado a una tormenta de diseño dada, debe estar restringido a un valor máximo tal que no supere el nivel de acera, a fin de garantizar la libre circulación de peatones y vehículos (Gómez et al. 2009). El objetivo principal de este trabajo es aplicar una metodología para estimar la peligrosidad pluvial a través de un índice cuantitativo distribuido espacialmente y calculado a partir de análisis multicriterio y de la ponderación de diversos factores que permitan una evaluación objetiva de la cuenca urbana mediante la comparación entre áreas críticas y la valoración de escenarios sobre la misma región. Para el caso de estudio, se seleccionó una subcuenca ubicada en la zona centro norte de la Ciudad de Coro, capital del Estado Falcón y se implementó un modelo de simulación integrado previamente calibrado a fin de obtener las profundidades y velocidades máximas de inundación en la red de calles, teniendo en cuenta la metodología propuesta por Zonensein et al. (2008). El dominio del Índice de peligrosidad (PI) y la escala afectan directamente a cada indicador debido a sus distintas naturaleza y unidades, por eso es indispensable que sean estandarizados o convertido a una escala común, de allí la importancia del proceso de normalización. Se plantearon modificaciones en las escalas de normalización del índice de profundidad denominado (I_Cot) manteniendo intactos los criterios de normalización para el resto de los indicadores de peligrosidad y se lograron mejores niveles de bondad en los ajustes propuestos por el mencionado autor para la normalización del índice (I_FP). Posteriormente, se definieron los pesos para cada indicador a partir de 3 escenarios críticos, que fueron analizados en función de los objetivos propuestos.

METODOLOGÍA

Se levantó información de campo durante eventos de lluvia ocurridos en la zona, patrones de flujo superficial en calles, y zonas cítricas a fin de validar la información obtenida en la simulación y además certificar los criterios de normalización para cada indicador.

Formulación del Indicador de peligrosidad asociada al flujo en calles (PI)

Se recomienda que la formulación no resulte altamente compleja desde el punto de vista matemático. Preliminarmente, se realizó una revisión exhaustiva de los criterios reportados en la literatura especializada sobre el tema y en función de esto, se optó por implementar un método basado en la ponderación mixta y fundamentada en las técnicas de análisis multicriterio propuestas por Zonensein et al. (2008):

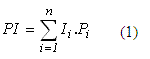
Donde Ii representa el indicador previamente normalizado, que compone el índice PI, varía en un rango de 0 como extremo mínimo y 100 como extremo máximo. En este caso se consideraron 3 índices: I_Cot (Índice de Profundidad de inundación), I_FV (Índice de velocidad ), I_FP ⁽Índice de Permanencia), n: número total de indicadores que componen el índice PI; y Pi: peso asociado al índice I_i , asignado en función de la importancia relativa.Atendiendo a razones prácticas, se variaron algunas de las nomenclaturas utilizadas por (Zonensein et al. 2008), Sin embargo, el aporte significativo del presente artículo radica en los criterios de normalización para cuantificar el índice de profundidad, ya que el enfoque expuesto por el mencionado autor, calcula la peligrosidad en la cuenca urbana, asumiendo un nivel fijo promedio para alturas de acera o bordillos lo cual dista mucho de la realidad y además, para láminas menores de 10 cm en un tramo de calle, asume que el efecto sobre el tránsito de vehículos y personas es nulo , lo cual no es totalmente cierto, entre otras razones porque para una velocidad directriz de un vehículo cercana a los 70 km/h y con alturas de lámina de agua de unos 5 mm, se puede presentar el fenómeno de «hidroplaneo» (FHWA 2009), que consiste en la pérdida de adherencia entre los neumáticos y la superficie del pavimento producto de la capa delgada de agua que sirve de interfaz entre estas dos superficies, este efecto es aun más propenso mientras la presión y la velocidad del vehículo se incrementan. Además, se busca optimizar los ajustes planteados por Zonensein et al. (2008) sobre las curvas de normalización para el cálculo del factor adimensional de permanencia (I_FP).

El método propuesto para la distribución de los pesos de cada sub índice fue el proceso de análisis jerárquico (AHP) (Saaty 1977) basado en el contexto del análisis multi-criterio. El uso de este método permitió no solo la determinación de los pesos para cada uno de los subíndices sino también realizar la prueba de consistencia que mide la coherencia lógica en el juicio y que a su vez reduce altamente el grado de objetividad propio de este tipo de procesos. El grado de consistencia GC mide cuantitativamente la importancia relativa de un sub índice respecto a otro. Este parámetro se calcula posterior a la distribución de los pesos y es función directa del número de sub índices. Para que una evaluación sea considerada lo suficientemente consistente debe cumplirse la condición GC < 10%, de lo contrario, el juicio subjetivo es considerado inconsistente (Saaty 1977).

La peligrosidad pluvial depende de tres factores, la profundidad del flujo o lámina de agua en la calle, la velocidad y la duración de la inundación por encima de cierto calado. Esta hipótesis fue probada analizando 3 escenarios y asignándole pesos diferentes a los indicadores correspondientes. La ecuación formulada por Zonensein et al. (2008) para el cálculo de la peligrosidad es la siguiente:

Estimación del indicador de profundidad (I_Cot): el criterio más utilizado para definir si en una determinada calle, no existe peligrosidad asociada al flujo de aguas pluviales para una probabilidad de ocurrencia dada, es el siguiente: tirante en calle y < altura de la acera (Dawson et al. 2008). La normalización de este indicador se fundamenta en criterio de expertos y observaciones de campo, simplificada por franjas sobre la base de un análisis detallado de daños posibles (absoluto y relativo) solamente en el intervalo y < 1 m.

El límite superior de la primera función está definida por la altura de la acera, luego la siguiente función cubre la franja que va desde 10 cm hasta 50 cm, en este nivel ya la inundación en la calle es total, y el flujo es capaz de afectar patios de fachada y estacionamientos, además en este nivel se comienza a interrumpir el tráfico regular de vehículos y sobre todo de personas. Se asume que de allí en adelante, cualquier lámina de agua superior a 50 cm invade completamente las viviendas y edificaciones con los respectivos daños que esto conlleva. En definitiva, se calculó este indicador comparando la función mostrada en la ecuación (3) con la curva normalizada propuesta por Zonensein et al. (2008) en la figura 1.

Estimación del indicador de velocidad o número del producto (I_FV): los criterios de peligrosidad basados en la consideración conjunta de calados y velocidades están ampliamente reportados en (FEMA 1979). Desde el punto de vista experimental, destacan los estudios experimentales publicados por ARMC (2000), Belleudy (2004) y el de Russo et al. (2011). Sin embargo, el primero que utilizó el término «número del producto» fueron Abt and Wittler (1989), para incluir el efecto combinado de las fuerzas hidrodinámicas ejercidas por el vector velocidad y la profundidad (v.y) sobre la estabilidad en los individuos. En base a estos estudios y a la normalización de este indicador propuesta por Zonensein et al. (2008) se elaboró la función de normalización por franjas con interpolación lineal para este indicador:

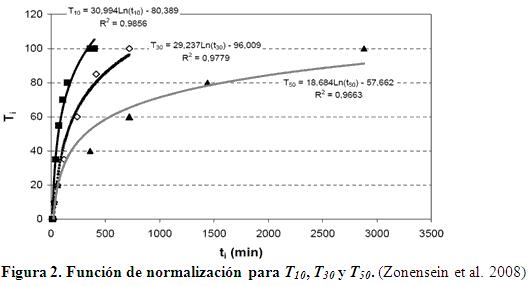
Estimación del indicador de duración de inundación (I_FP): considera los minutos / horas / días que una calle permanece inundada al menos ciertos cm de profundidad, considerando 3 elementos en riesgo: los peatones, que son los primeros en verse afectados ya que las zonas inundadas con pequeñas láminas de agua son suficientes para dificultar o impedir su tránsito regular por las aceras, en segundo lugar los vehículos que al circular por zonas de encharcamiento causan tranques en el tráfico e incrementan el peligro de que se presente el fenómeno de «hidroplaneo», y por último las viviendas o edificaciones expuestas frontalmente a la calle. Para obtener el valor de este indicador se definen los tiempos indicativos de efectos potenciales sobre peatones (t₁₀), el tráfico (t₃₀) y las viviendas (t₅₀). Estos se refieren al tiempo en minutos durante el cual un área permanece inundada con una lámina mayor de 10 cm, 30 cm y 50 cm respectivamente. Se destaca que para un hidrograma característico (modelo campana) transitando en cualquier calle de la cuenca, e incluso para cualquier lámina superior a 50 cm, se cumple que t₁₀ > t₃₀ > t₅₀. La normalización formulada por Zonensein et al. (2008) en este caso fue por franjas de tipo logarítmicas (figura 2), sin embargo, el autor considera que para este tipo de ajustes, la correlación entre los datos puede mejorarse empleando otro modelo matemático.

En tal sentido, se probaron distintos modelos orientados a perfeccionar los niveles de confiabilidad, el coeficiente de correlación y reducir el error cuadrático medio. Cabe resaltar que, posterior a la revisión del estado actual de la temática, no se encontraron reportes que justifiquen el origen de los valores límites establecidos en la normalización logarítmica adoptada para los subíndices T₁₀, T₃₀ y T_50, cabe destacar que estos tres subíndices representan los correspondientes valores normalizados en escala del 1 al 100, durante los cuales permanece inundada una calle con una profundidad mayor que 10, 30 y 50 cm. Los parámetros sugeridos por Zonensein et al. (2008) para cada función ajustada se muestran en la gráfica:

Caso de aplicación en una subcuenca urbana de la ciudad de Coro

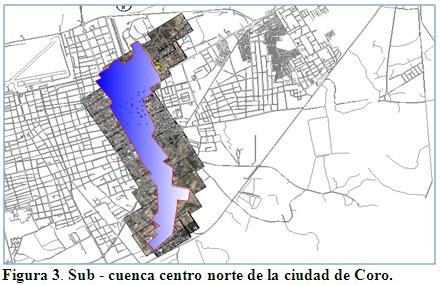
La región seleccionada para este estudio fue la ciudad de Coro, capital del Estado Falcón, ubicada en la costa norte de Venezuela. El sistema de drenaje de la ciudad está constituido por 30 canales tanto artificiales como naturales, y más de 5 kilómetros de colectores enterrados que atraviesan la ciudad en varias direcciones y que conducen las aguas pluviales a los sitios de vertido final. La topografía urbana de la ciudad hace que aproximadamente el 70% de la escorrentía de origen pluvial drene a través de calles y colectores enterrados hacia el noreste y el resto fluya en dirección oeste en donde predominan los canales artificiales y naturales. La cuenca seleccionada pertenece al sistema centro norte de la ciudad, tiene un área de aporte aproximada de 108,99 ha y está delimitada por la avenida Tirso Salavarría, calle Garcés- avenida Independencia y el sector Los Orumos, figura 3.

Se construyó el modelo digital de elevaciones (MDE) de la subcuenca seleccionada, (Sánchez y Méndez 2009). Se confeccionó el modelo conceptual del sistema real y se discretizó la cuenca en un total de 122 subcuencas con fracciones impermeables que varían entre 40 y 65% y valores del parámetro hidrológico Curva Número (CN) del Soil Conservation Service (SCS) de los Estados Unidos, variando entre 75 y 85. Para obtener la distribución espacial de la peligrosidad en calles, se elaboraron los mapas temáticos respectivos para cada indicador. Para este nivel de análisis y en correspondencia con la escala espacial de decisión adoptada, se estimaron valores medios en los polígonos que representan cada calle o tramo de calle, por lo tanto, al definir el dominio del índice por calles, se trata de un proceso agregado ya que la simulación hidráulica se basa en el análisis de tramos rectos de calles funcionando hidráulicamente como canales. Para obtener los calados o láminas en calles se calibró el Modelo EPA- SWMM y se simuló la respuesta del sistema de drenaje ante una tormenta de duración e intensidad similar a la del evento utilizado para calibrar.

Calibración del modelo y simulación del evento ocurrido 01-02-2009 en la cuenca centro-norte de Coro

Previo al análisis de peligrosidad, se implementó y calibró el modelo SWMM, a partir del hietograma de tormenta para un evento específico registrado el 01-02-2009 y del hidrograma de salida conocido en el nodo de descarga del sistema. Esta cuenca se caracteriza por tener una topografía plana, con pendientes del orden del dos por mil, con un área de aporte cerrada que facilita la correcta cuantificación del escurrimiento urbano. El nodo de vertido se localiza en la avenida Alí Primera, específicamente detrás del Estadio Municipal J. M. Ugarte, en las cercanías del Instituto Universitario de Tecnología Alonso Gamero (IUTAG). Con el levantamiento topográfico, se constató que el sitio de descarga posee la cota más baja de toda la cuenca seleccionada, esto hace suponer que toda la escorrentía que circula por las calles tiene posibilidad de ingresar al colector a través de las obras de captación (sumideros). Por otro lado, la cantidad de agua que queda almacenada o retenida en calles, avenidas, y depresiones naturales o artificiales, sumada a la porción de agua que se infiltra en las pocas áreas permeables, representan volúmenes importantes que no llegan a ingresar al sistema superficialmente.

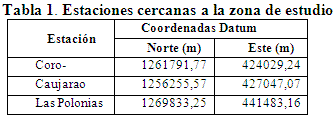
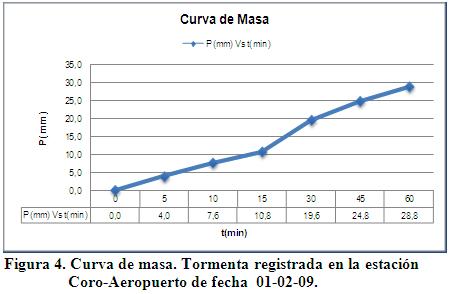
El caudal máximo observado en el nodo de descarga fue de 552 litros por segundo con un tiempo al pico aproximado Tp =1 hora y 15 minutos. A partir de las coordenadas geográficas respectivas, se determinó la influencia espacial de las estaciones climáticas en la cuenca urbana mediante la construcción de los polígonos de Thiessen con las estaciones más cercanas a la zona de estudio: Estación Coro-Aeropuerto, Estación Caujarao y Estación Las Polonias (tabla 1), resultando la Estación Coro Aeropuerto la única con influencia de 100% sobre la cuenca. Los datos de lluvia registrados se muestran en la figura 4.

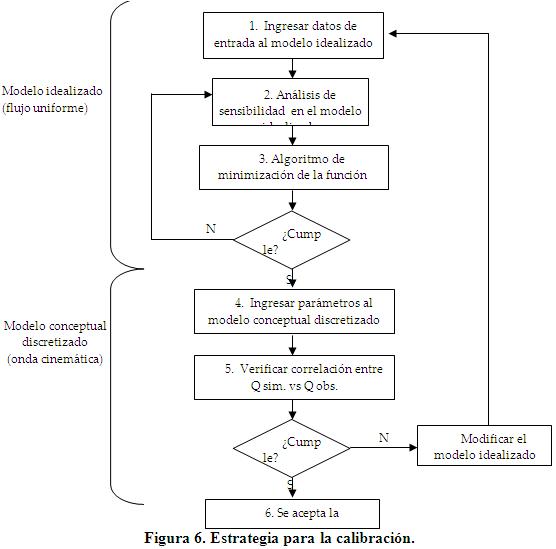
Definición de la estrategia de calibración. La cuenca se desagregó para una escala computacional de detalle conformada por 122 subcuencas, sin embargo para realizar la prueba de sensibilidad y obtener una combinación de valores promedios para los parámetros, se construyó un modelo conceptual simplificado o idealizado representado por subcuencas o segmentos dispuestos como dos planos asimétricos que aportan de manera concentrada a un canal de drenaje. Para ello, se implementó un esquema de solución apoyado en las ecuaciones que rigen el módulo de cálculo hidrológico «Runoff» del SWMM para flujo uniforme. Considerando que el SWMM no cuenta con un algoritmo para la calibración automática, se optó por diseñar una estrategia a base de 6 etapas principales combinando la respuesta hidrológica de los dos modelos conceptuales. La primera consiste en ingresar los datos de entrada al modelo conceptual idealizado o modelo preliminar, figura 6, (condiciones de frontera, parámetros, geometría y estructura del sistema). Luego, se procede a efectuar el análisis de sensibilidad para seleccionar los parámetros a ser calibrados, en este tipo de estrategia pueden identificarse y escogerse parámetros de naturaleza hidrológica o hidráulica según la respuesta del modelo. Conviene resaltar que los parámetros que se introducen en el modelo pueden servir para ajustar la respuesta del mismo, por ejemplo el ancho W corresponde a la anchura del depósito que está representando a una determinada subcuenca (figura 5) y que debe estimarse a partir de la forma geométrica real de la misma, que no será ni uniforme ni completamente simétrica. Sin embargo, como se conocen realmente los valores los parámetros geométricos que dependen exclusivamente de la representación que se haga del sistema físico real, conviene usar otras variables para el ajuste, como por ejemplo el coeficiente de rugosidad de Manning, o los parámetros que influyen en las pérdidas por infiltración.

En este caso, se calibró la rugosidad para las áreas permeables e impermeables de la cuenca y el parámetro curva número (CN). Con los parámetros seleccionados se busca una función objetivo orientada a reducir la discrepancia entre los gastos modelados y medidos, para finalmente implementar un algoritmo de calibración que minimice su diferencia. Los valores obtenidos en el análisis sobre el modelo simplificado son introducidos en el modelo conceptual discretizado (sistema real) y se ejecuta la simulación del evento para verificar la calidad de la calibración en base al nivel de correlación entre los valores simulados y observados

La función objetivo seleccionada (ecuación 6) le indica al algoritmo de optimización qué tan cerca está de llegar a los parámetros óptimos, en este caso se utilizó el criterio de los mínimos cuadrados como función objetivo y un proceso iterativo basado en ensayo y error o aproximaciones sucesivas para su minimización.

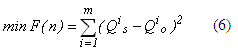
donde Q ⁱ_s: gasto simulado para el instante «i»; Q ⁱ_o: gasto observado para el instante «i»;

m: instante final del periodo de calibración.

Escenarios analizados para el cálculo de la peligrosidad

Para una profundidad de lluvia de 28,8 mm y una duración de 60 min, se analizaron 3 grupos de pesos representando diferentes criterios sobre la importancia relativa de los indicadores de peligrosidad. Aplicando el método de análisis jerárquico (AHE) se establecieron estos 3 grupos que cubren todo el espectro de casos en respuesta a los objetivos propuestos en esta evaluación, es decir, se analizaron 3 juegos de valores combinando el nivel de importancia relativa de los índices a fin de ponderar su influencia en una cuenca bajo el escenario de lluvia adoptado. Cabe destacar que la cantidad de escenarios va a depender siempre de los objetivos del estudio y es potestad del que gestiona el sistema de drenaje. En el primer escenario, se supone que I_Cot es extremadamente más importante que I_FP pero un poco menos importante que I_FV, que a su vez se considera más importante que I_FP. Para el segundo escenario, se acepta que I_Cot es un poco más importante que I_FP y un poco menos importante que I_FV, que a su vez se considera más importante que I_FP. Finalmente, para el tercer escenario se adjudica igual importancia a los tres indicadores. La tabla 2 explica con detalle cada uno de estos escenarios.

ANÁLISIS Y DISCUSIÓN DE RESULTADOS

El parámetro CN incluido en el modelo de pérdidas fue calibrado a partir de la lámina de escorrentía directa LED = 3,362 mm obtenida con el volumen total observado Vol = 3662,46 m³ durante el evento, dando como valor promedio para toda la cuenca un valor de CN = 88,1. La prueba de sensibilidad sobre el modelo idealizado para «n permeable e impermeable» y la evaluación de la función objetivo se exponen en las gráficas correspondientes (figura 7).

En la gráfica (a) se observa claramente el solapamiento de las funciones para valores de n permeable en el intervalo (0,3 0,6) presentando un mínimo global para una abscisa de 0,02. Igualmente, se aprecia en la gráfica (b) que la función tiene una variación asintótica a partir de valores de rugosidad en la zona permeable n perm = 0,3. Seguidamente, en la gráfica (c) se muestra la comparación entre hidrogramas simulados y observados para el modelo idealizado asignando los parámetros óptimos definitivos (n impermeable = 0,02 y n permeable = 0,3) para los cuales se hace mínima la función objetivo.

Esta prueba preliminar sirve como punto de partida para el ajuste del modelo conceptual discretizado, en el cual de ser necesario y en función de la correlación se debe ir ajustando hasta alcanzar un ajuste aceptable. Sin embargo, los resultados de la simulación luego de asignar estos parámetros como valores medios en las subcuencas, se muestran en la figura 8, lo cual evidencia un ajuste aceptable.

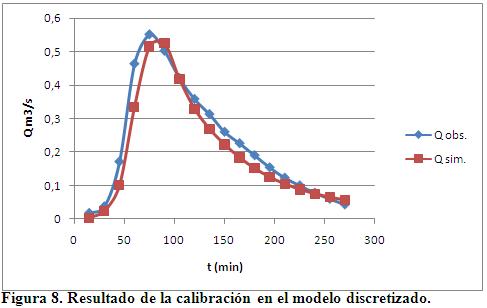
Al comparar las series de gastos en la salida del modelo se puede observar para la primera corrida un acercamiento evidente entre las dos funciones, y un patrón análogo tanto en la rama ascendente del hidrograma como en la parte descendente, lo que demuestra que el análisis de sensibilidad realizado en el modelo preliminar idealizado constituye una técnica viable para seleccionar el primer juego de parámetros. Para esta corrida, el coeficiente de correlación fue de 0.961.

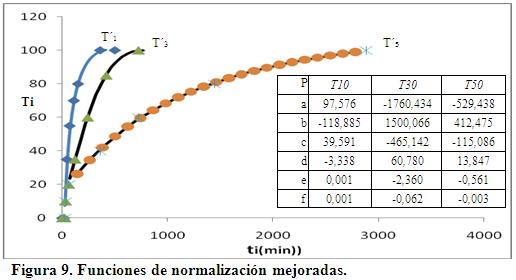
Por otra parte, al analizar diversos modelos y realizar el tratamiento estadístico de los datos, se aplicó una estrategia orientada a homologar el criterio de ajuste para las tres funciones (ecuación 7) bajo el mismo modelo matemático. Si se asigna como variable dependiente normalizada T´ a la nueva función, la estructura de la ecuación (7) con los parámetros (a, b, c, d, e, f) y sus respectivas curvas modificadas se resumen en la figura 9, donde T´₁, T´₂, T´₃ corresponden a las funciones normalizadas mejoradas para calcular T₁₀, T₃₀, T₅₀ respectivamente.

La comparación entre los coeficientes de correlación permite evaluar la bondad del modelo de regresión obtenido por Zonensein et al. (2008) con el modelo propuesto por el autor para un 95% de confiabilidad. En tal sentido, queda demostrado en la tabla 3 el aporte realizado para disminuir la incertidumbre en la predicción de la variable dependiente dentro del dominio establecido. Es preciso resaltar que los valores de R² se obtuvieron del respectivo análisis estadístico, a partir de la serie de datos reportada en Zonensein et al. (2008) en la figura 2.

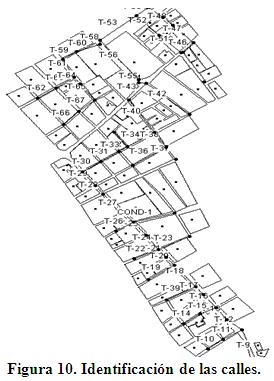
Los resultados del modelo proporcionan información sobre la evolución temporal de la profundidad de inundación y de la velocidad media en cada calle durante el período de simulación. El mapa de la figura 10 sirve de referencia para identificar cada una de las calles evaluadas, en este caso la codificación para simular los conductos en el modelo comienza con la letra «T» seguida de un guión y del número de la calle.

Los mapas de la figura 11, muestran las inundaciones localizadas en los puntos más críticos del período, considerando un tratamiento hidráulico para las calles de mayor importancia en función del volumen vehicular y un tratamiento hidrológico para el resto de las calles.

Este enfoque permite incluir algunas calles secundarias (de menor importancia) como una fracción del área impermeable dentro de la conceptualización y discretización de las sub cuencas y no como parte de los conductos que transitan superficialmente los gastos a través del sistema de drenaje. Se evidencia que la zona donde se presentan láminas de agua superiores a 15 cm es hacia el noreste de la cuenca (calle 40 y 56), alcanzando una profundidad máxima de 0,19 m.

Se observan tramos con tirantes que no superan el nivel de acera en la mayoría de los tramos de calle analizados presentando velocidades bajas propias de zonas planas que van desde un mínimo de 0,10 m/s hasta 1 m/s (calle 54) con promedio total de la cuenca de 0,35 m/s. En la figura 12, se observan notables variaciones entre los dos casos analizados, al incluir dentro de las escalas de normalización el impacto de los tirantes que están en 15 y 30 cm ( calles 40, 43, 56), queda en evidencia que los criterios de Zonensein et al. (2008) subestiman el efecto de laminas inferiores al nivel promedio de acera, ya que las escalas normalizadas por dicho autor para I_Cot, arrojan valores poco significativos (I_Cot < 8), para los tirantes analizados y minimiza las pequeñas variaciones que tiene el tirante en este rango.

Los resultados del indicador de permanencia de inundación así como los del indicador de velocidad se muestran en la figura 13 y su comportamiento espacial, aunque coincide con lo esperado sobre todo en las zonas de baja pendiente y en las zonas de encharcamiento no representa un problema relevante en los tramos de calle estudiados ya que su magnitud no supera en ningún caso el intervalo I_FP < 0,5 para el evento de lluvia analizado.

Se observa además que los pesos asignados según Zonensein et al. (2008) a los factores de ponderación en la formulación del indicador I_FP están enfocados solo al daño sobre viviendas, subestimando el impacto que tiene sobre el tránsito de vehículos y personas, esto se explica en la distribución de los pesos establecidos para cada factor, en este caso 0,68 para T50, 0,22 para T30 y solo 0,10 para el T10. Finalmente, los mapas de peligrosidad, figura 14, correspondientes a los escenarios 2 y 3 no muestran diferencias importantes, no obstante, el escenario 1 si arrojó resultados contrapuestos evidenciando la sensibilidad del índice a la asignación de los pesos. Por otro lado, se observa que para los tres escenarios, existe coincidencia en la identificación de zonas con mayor peligrosidad.

 

CONCLUSIONES

La metodología aplicada permitió conocer en la zona estudiada, la distribución espacial del indicador de peligrosidad pluvial asociada al flujo superficial en calles mediante una gama de colores, lo queLeer fonéticamente

constituye una herramienta valiosa para respaldar la toma de decisiones por parte de los gestores del sistema de drenaje pluvial urbano.

El análisis realizado sobre el modelo conceptual de la subcuenca urbana, evidenció la sensibilidad del parámetro de profundidad (I_Cot) en relación con la escala de normalización adoptada en el rango 0 < y < 15 cm, en función de los tirantes simulados.

En cuanto a la ponderación de los indicadores, se demostró el valor que tiene precisar claramente cuáles son los elementos en riesgo y la magnitud de la afectación potencial, ya que los resultados pueden llegar a subestimar los efectos perjudiciales sobre algunos actores importantes (tránsito de vehículos y personas).

Las validaciones de campo indican que la metodología puede ser considerada como eficaz, no obstante, a pesar de que el método es adaptable a diferentes percepciones de los gerentes, las escalas de normalización en todos los casos deben responder a criterios objetivos a fin de mitigar este aspecto frágil del índice, sin embargo, esta clase de formulaciones se hace aún más sólida cuando se dispone de información de campo que permita validarla.

Finalmente, se demuestra que a partir de los mapas presentados, se viabiliza la toma de decisiones en relación con la ejecución de medidas estructurales para rehabilitar el sistema de drenaje en función de modificar el mapa de peligrosidad y se facilita la definición de rutas de emergencia que pueden ser utilizadas en casos de eventos extremos de lluvia.

 

 

REFERENCIAS

Abt, S.R. and Wittler R. J., «Predicting human instability in flood flows», Hydraulic Engineering, Proceedings 1989 National Conference on Hydraulic Engineering, ASCE, (1989).

ARMC, «Floodplain management in Australia. Best practice principles and guidelines», Australia: Agricultural and Resource Management Council of Australia and New Zealand , SCARM Report 73, (2000), 105 pp.

Belleudy, P., «Risques Hydro-météorologiques, crues et inondations / risque, aléa et vulnérabilité», DDS-TUE364- 9, Suiza, (2004).

Dawson, R. J.; Speight, L.; Hall, J. W.; Djordjevic, S. and Savic, D., «Attribution of flood risk in urban areas», Journal of Hydroinformatics, ASCE, (2008), Vol. 10, No 4, pp. 275-288.

FEMA, «The floodway: a guide for community permit officials», Federal Emergency Management Agency, U.S. Federal Insurance Administration, Community Assistance, No 4, (1979), 156 pp.

FHWA, «Urban Drainage Design Manual», Federal Highway Administration, U.S. Department of Transportation. Publication No. FHWA-NHI-10-009, (2009), 478 pp.

Gómez, M.; Macchione, F. y Russo, B., «Comportamiento hidráulico de las calles durante lluvias extremas en zonas urbanas», Ingeniería Hidráulica en México, (2009), Vol. XXIV, No. 3, pp. 51-61.

Hauger, M.B., «Indicators of hazard, vulnerability and risk in urban drainage», Water science and technology, (2006), Vol. 54, No 6-7, pp. 441-450.

Russo, B., Gómez, M. and Macchione, F., «Experimental approach to determine flood hazard criteria in urban areas», 12th International Conference on Urban Drainage, Porto Alegre, Brazil, (2011).

Saaty, T. L., «A scaling method for priorities in hierarchical structures». Journal of Mathematical Psychology, (1977), Vol. 15, No.15, pp. 234-281.

Samuels, P., «Flood risk analysis and management achieving benefits from research», European Conference on Floods, GOCE-CT-2004-505420, Viena, Austria, (2006), 17-18.

Sánchez, L. y Méndez, L., «Modelo de elevación digital e informatización del sistema de drenaje mayor y menor de la zona oeste de la ciudad de Santa Ana de Coro, Falcón.», Trabajo de Investigación, UNEFM, Coro, Venezuela, (2009), 230 pp.

Sánchez, L., «Un nuevo enfoque del método de ponderación mixta en la determinación de la peligrosidad a las inundaciones pluviales en una cuenca urbana», Centro de Investigaciones en Recursos Hídricos (CIDRHI), UNEFM, reporte 01-2011, Coro, Falcón, Venezuela, (2011) .

Zonensein, J.; Miguez, M.G.; De Magalhães, L.P.C. and Valentin, M.G., «Flood risk index as an urban management tool», 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK. (2008).

 

 

Recibido: 14 de mayo de 2012
Aprobado: 19 de mayo de 2012

 

 

Luis Alejandro Sánchez Román, Yoel Martínez González, Centro de Investigaciones de Recursos Hídricos (CIDRHI) Universidad Nacional Experimental Francisco de Miranda, Falcón, Venezuela, Centro de Investigaciones Hidráulicas (CIH), Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba, email: [e-mail] , email: [e-mail]