Artículo Original

Curvas de intensidad, duración y frecuencia de la estación meteorológica Puyo

Curves of intensity, duration and frequency of Puyo meteorological station

Jairo Miguel Maldonado Erazo¹  , Jairo Rafael Samaniego Merchán²  , Diego Mauricio Ramos Criollo³  , Ricardo Vinicio Abril Saltos⁴ 

¹Técnico Regional Pastaza, Inst. Nac. de Meteorología e Hidrología, (INAMHI) Pastaza, Ecuador.

²Profesional independiente, Pastaza, Ecuador.

³Estudiante Universidad Estatal Amazónica, Carrera de Ingeniería Ambiental, Pastaza, Ecuador.

⁴Docente Universidad Estatal Amazónica, Carrera de Ingeniería Ambiental, Pastaza, Ecuador.

RESUMEN

Este trabajo se desarrolló en la estación meteorológica Puyo, Pastaza, Ecuador. Su objetivo fue determinar las curvas de intensidad duración y frecuencia para períodos de 2,5,10,25,30,50 y 75 años. Se analizaron los registros horarios del pluviógrafo del período 1987- 2018 y se establecieron las intensidades para 1, 2, 4, 6, 8, 12 y 24 horas, se determinaron los estadísticos media y desviación estándar y se aplicó el método de ajuste probabilístico de Gumbel. La estación reportó láminas medias de 51,1 y 139,1 mm para 1 y 24 horas con máximas de 75 y 177,7 mm, las proyecciones a 75 años plantean intensidades con valores de 88,4 y 8,9 mm respectivamente. Se concluye que la estación presenta valores que sobrepasan las intensidades de 50 mm/h para periodos de 1 h.

Palabras-clave: Gumbel; lluvia; periodo de retorno; probabilidad

ABSTRACT

This work was developed in the Puyo meteorological station, Pastaza, Ecuador. Its objective was to determine the intensity and frequency curves for periods of 2,5,10,25, 30, 50 and 75 years. The hourly records of the pluviograph for the 1987-2018 period were analyzed, intensities were established for 1, 2, 4, 6, 8, 12 and 24 hours, the mean statistics and standard deviation were determined and the Gumbel probabilistic adjustment method was applied. The station reported average rainfall depths of 51,1 and 139,1 mm for 1 and 24 hours with maximums of 75 and 177,7 mm, the projections to 75 years raise intensities with values of 88,4 and 8,9 mm respectively. It is concluded that the station presents values that exceed the intensities of 50 mm/h for periods of 1 h.

Key words: Gumbel; rain; return period; probability

INTRODUCCIÓN

Las características hidrometeorológicas de una localidad son factores influyentes para una adecuada gestión de recursos hídricos, planificación y ordenamiento territorial (^{Martínez y Villalejo 2018}), donde las curvas de intensidad duración y frecuencia permiten determinar las máximas intensidades que después se convierten en instrumentos para el diseño de obras de drenaje urbano y estimación de caudales de evacuación en pequeñas cuencas rurales (^{Campos 2010}).

La Organización Meteorológica Mundial, ^{OMM (2015)}, recomienda utilizar series de al menos 30 años y ^{Pizarro et al. (2003)} recomiendan que los periodos de retorno a calcular, no excedan el doble o el triple de la longitud de datos de la serie a estudiar.

En periodos de retorno de precipitaciones extremas y curvas IDF es necesario introducir el concepto de probabilidad para poder evaluar riesgos. ^{Sánchez (2017)} plantea que en el estudio de las precipitaciones como generadoras de caudales excepcionales (avenidas), se deben considerar las máximas diarias (el día más lluvioso de cada año), para aumentar el detalle hasta períodos de horas. La intensidad de la lluvia se puede expresar como “la tasa temporal de precipitación, o la profundidad por unidad de tiempo (mm/h o pulg/h)” según ^{Chow et al. (1994)} o también “cantidad de lluvia, expresada en unidades de altura por unidad de tiempo” según ^{Torregrosa (2014)}.

La representatividad de una observación meteorológica como lo define la Organización Meteorológica Mundial, ^{OMM (2014)}, es el grado de exactitud con el que describe el valor de una variable necesaria para una finalidad específica y que en el caso de aplicaciones de pequeña escala o local la dimensión del área que será tomada en cuenta puede ser de 10 km o menos.

^{Chow et al. (1994)} plantean dos métodos de construcción de las curvas IDF. El primero considera un análisis de frecuencias de precipitaciones con la utilización de una función de distribución de probabilidades de valores extremos como Gumbel. En su segundo método expresa a las curvas IDF como ecuaciones, con el fin de evitar la lectura de la intensidad de lluvia de diseño en una gráfica.

La distribución de Gumbel es utilizada para calcular valores extremos, partiendo de una base de datos de niveles máximos. Este método probabilístico es muy utilizado para el cálculo de valores máximos de precipitaciones, caudales, velocidades de vientos entre otros; estas proyecciones son empleadas en distintas aplicaciones de la ingeniería, como para la construcción de diferentes obras, construcción de redes de alcantarillado, diques, hidroeléctricas, puentes. Además, es un insumo para estudios probabilísticos como la frecuencia de inundaciones de una cuenca hidrográfica, fenómenos costeros etc. (^{Torregrosa 2014}).

^{Chow et al. (1994)} expresa estas distribuciones de la forma:

$X=Xm+Dx$ (1)

donde:

X	- valor máximo (precipitación) para un período de retorno T, con una probabilidad proporcionada.
Xm	- media de la base de datos de precipitaciones máximas.
Dx	- desviación respecto a la media, que se estima mediante el producto:

$Dx=k*s_{n-1}$ (2)

donde:

K	- factor de frecuencia definido por cada distribución. Es una función del nivel de probabilidad asignada a X.
𝑠𝑛−1	- desviación estándar de la serie.

En Ecuador los estudios sobre curvas IDF son escasos, teniéndose únicamente el planteado por ^{Guachamín et al. (2015)}, donde se analizó para la estación Puyo la serie de datos de 1964 al 2010, determinaron a través de la función logarítmica las intensidades en 5, 10, 15, 20, 30, 60, 120, 360 y 1440 minutos a períodos de 2,5,10,25,50 y 100 años.

El presente trabajo tuvo como objetivo establecer las curvas de Intensidad, Duración y Frecuencia de la estación Puyo, tomando como base los registros del período 1987-2018 con proyecciones a 2,5,10,25,30,50 y 75 años.

CARACTERIZACION DEL LUGAR

El área de representatividad abarca un radio de aproximadamente 10 km (figura 1) tomando como origen el lugar donde se encuentra emplazada la estación meteorológica INAMHI-Puyo en las coordenadas geográficas decimales: latitud: -1,505580 m, longitud: -77,958283 m, ubicada en la parroquia rural de Veracruz, perteneciente al cantón Pastaza y a la provincia de Pastaza.

Figura 1 Localización y área de representatividad 

Procesamiento de la información

Se tomó la información disponible de los registros horarios del pluviógrafo marca Thiess del período 1987 a 2018, de la estación meteorológica Puyo, los cuales fueron transcritos en una hoja de cálculo de Excel. La información fue resumida y se obtuvieron los valores máximos anuales en rangos horarios de 1, 2, 4, 6, 8, 12, 24 horas. Se estimaron las intensidades en mm/h dividiendo los valores por su duración horaria. Para cada rango horario se estimó la media y desviación estándar. El comportamiento para cada duración horario se analizó mediante tendencia lineal en función de los años de datos.

Se aplicó un método probabilístico como la representación de cada uno de los elementos de la muestra, donde se utilizó la distribución de Gumbel, que en climatología es utilizada para predecir con cierta probabilidad los valores que pueden tomar las precipitaciones en un tiempo futuro (^{Darba 2006}). Para la determinación de los parámetros requeridos por el modelo de Gumbel, se utilizaron las siguientes ecuaciones.

$F\left(x\right)=e^{-e^{-y}}$ (3)

donde:

y	- variable reducida, dada por la ecuación (4).
e	- constante de Neper.
F(x)	- probabilidad de que un valor sea igualado o excedido.

La variable reducida viene expresada en función del período de retorno:

$y=-ln\left(ln\left(T/\left(T-1\right)\right) \right)$ (4)

$\mu =Xm-\left(\frac{yn}{\alpha }\right)$. (5)

$\alpha =\frac{Sn}{S_{n-1}}$. (6)

donde:

yn=0,536 Sn=1,112	- (Para una longitud de datos de 31 años para cada duración horaria )
μ	- moda de la distribución.
α	- parámetro de dispersión.
Xm	- media de la base de datos de precipitaciones máximas.
S n	-1 - desviación estándar de la serie.
yn	- valor medio esperado de la variable reducida.
Sn	- desviación estándar de la variable reducida.

La función de distribución de probabilidad se utiliza para deducir el comportamiento futuro de una serie histórica de datos climatológicos partiendo de la observación de una muestra, dicho de otra manera, la conducta de las variables aleatorias discretas o continuas se representa con modelos de distribución de probabilidad (^{Gorgas et al. 2011}). La función utilizada es la de Gumbel que se comporta de la siguiente manera (^{Chow et al. 1994}):

$P\left(x\le X\right)=F\left(X\right)=e^{-e^{-y}}$ (7)

Finalmente se obtiene:

$X=Xm+k*S_{n-1}$ (8)

$X=Xm+Dx$ (9)

donde:

Dx	- desviación respecto a la media, que se estima mediante el producto.

La variable Dx está dada por:

$Dx=k*S_{n-1}$ (10)

$k=\frac{\left(y-yn\right)}{Sn}$ . (11)

donde:

K	- Factor de frecuencia definido por cada distribución. Es una función de nivel de probabilidad asignado a X.

Construcción de la curva de intensidad, duración y frecuencia

La metodología utilizada para la construcción de las curvas IDF fue la citada por ^{Pizarro et al., (2003)}, para lo cual en cada año del período evaluado se identificó la mayor lamina de lluvia acumulada de precipitación para duraciones de 1, 2, 4, 6, 8, 12 y 24 horas. Posteriormente para la obtención de las intensidades se dividió cada uno de estos valores entre la duración horaria que representa. Se establecieron para cada duración los estadísticos media y desviación estándar. Los parámetros de dispersión, posición y demás variables necesarias que se requirieron para la función de distribución de probabilidad de Gumbel se obtuvieron aplicando la ecuación (4) para el valor de y, ecuación (10) para Dx y ecuación (11) para k.

Se realizó la proyección de las intensidades para las duraciones indicadas en los períodos de retorno 2, 5, 10, 25, 30, 50 y 75 años, para lo cual se aplicaron las ecuaciones (8), (9), (10) y (11). El valor de y se estableció en función de los períodos de retorno de 2, 5, 10, 25, 30, 50 y 75 años, mientras que los valores de Yn y Sn se establecieron para el valor de 31 que corresponde a la longitud de datos existente. El análisis de frecuencias de precipitaciones se realizó con el modelo estadístico de distribución de probabilidades de Gumbel. Unas vez obtenidas y definidas las variables necesarias, utilizando el software Microsoft Excel, se representaron de manera gráfica las curvas de intensidad-duración-frecuencia para la estación meteorológica Puyo.

LÁMINAS E INTENSIDADES REPORTADAS

La figura 2 muestra el comportamiento histórico de las intensidades para duraciones de 1, 2, 4 y 6 horas, donde al aplicarse una línea de tendencia lineal se observa un incremento de las intensidades para duraciones de 1 h y 2 h, mientras que, para el resto de los períodos horarios, la tendencia no muestra incremento ni decremento de los valores. A su vez muestra los valores más altos para duración de 1 h de 75 mm/h en el año 2005, para 2 h en el año 2009 con 47,8 mm/h, para 4 h con 34,7 mm/h en el 2007 y para 6 h de 26,3 mm/h en 1992.

La figura 3 muestra el comportamiento histórico para intensidades de 8, 12 y 24 horas, en estos no se aprecia una tendencia creciente o decreciente y los máximos valores reportados son para duraciones de 8 h de 20,3 mm/h y para 12 h de 13,8 mm/h, ambos en 1992 y para 24 h de 7,4 mm/h en el año 1990.

La tabla 1 presenta las precipitaciones máximas en mm del período 1987-2018 registrados en la estación meteorológica Puyo para duraciones de 1, 2, 4, 6, 8, 12 y 24 horas. Los eventos con mayor relevancia fueron en 2005 para duración de 1 h, 2009 para duración de 2 h, 2007 para duración de 4 h, 1991 para duración de 6 h, 1992 para 8 h y 12 h y 1990 para 24 h. Los registros de 1997 no se utilizaron debido a la ausencia de esta información en la base de datos de la estación meteorológica.

En la tabla 2 se observan las intensidades para duraciones de 1, 2, 4, 6, 8, 12 y 24 horas para el período evaluado. A partir de los registros históricos, se calcularon los estadígrafos media (X) y desviación estándar (Sn-1), se observa que ambos valores disminuyen a medida que se incrementa la duración de la precipitación.

Figura 2 Registro histórico de intensidades para duraciones de 1 h, 2 h, 4 h y 6 h 

Figura 3 Registro histórico de intensidades para duraciones de 8 h, 12 h y 24 h 

La tabla 3 presenta los valores probables de intensidades, asociadas con periodos de retorno de (2-30 años), para duraciones de 1 hora, la cuantificación de estos datos fue realizada con el objetivo de determinar la variación de las precipitaciones a lo largo del tiempo. Para ilustrar el comportamiento de los valores máximos para los diferentes periodos de retorno se hace referencia al comportamiento de las precipitaciones máximas a 1 hora en los periodos de retorno de 2 y 30 años. Se observa que para un periodo de retorno de 2 años el valor máximo a presentarse es de 49,7 mm/h con una probabilidad de excedencia de 50 %, por otro lado, para un periodo de retorno de 30 años el valor máximo a presentarse es de 79,3 mm/h con una probabilidad de 3,33 % de que se supere el valor estimado. Se deduce además que la diferencia entre el 100 % y la probabilidad de excedencia dará como resultado la probabilidad de no excedencia de los valores máximos previstos para cada periodo de retorno.

Tabla 1 Precipitaciones máximas (mm.) del período 1987-2018 de Puyo 

Horas Años	1h	2h	4h	6h	8h	12h	24h
1987	40,5	65,6	90,7	104,0	121,4	146,8	161,2
1988	46,1	65,0	98,1	109,9	122,5	123,8	160,1
1989	37,5	66,0	88,9	123,7	126,6	128,7	158,6
1990	60,5	91,6	98,2	98,4	101,1	109,7	177,7
1991	68,9	82,8	93,5	99,3	101,3	123,5	148,2
1992	46,3	69,5	130,3	157,6	162	165,1	165,2
1993	33,2	56,6	67,7	69,6	69,6	72,0	89,0
1994	43,5	56,7	64,2	77,9	83,7	96,8	105,0
1995	36,9	50,3	77,1	77,4	79,5	93,2	130,0
1996	39,4	58,1	85,7	104,1	113	118,1	140,7
1998	46,7	80,5	121,7	134,5	141,9	145,3	147,7
1999	46,5	59,4	82,3	88,0	91	97,4	107,0
2000	38,0	56,6	70,8	103,9	120,2	129,5	136,1
2001	54,0	81,9	120,9	129,9	131,7	132,6	136,9
2002	41,5	59,3	60,5	67,4	67,6	91,3	113,0
2003	52,1	81,8	113,4	113,9	121	122,0	136,2
2004	61,6	76,6	78,2	91,6	101,9	121,3	133,5
2005	75,0	94,8	98,5	99,6	99,7	112,9	174,6
2006	59,0	72,6	78,5	78,5	82,1	100,6	117,9
2007	63,7	89,5	138,7	150,9	151,7	163,7	163,7
2008	68,0	89,8	105,6	108,6	116,3	119,4	123,0
2009	63,0	95,5	136,5	149,3	150	150,4	151,8
2010	53,7	81,7	115,1	120,3	121,9	128,3	140,5
2011	65,7	94,1	103,3	103,8	125,8	133,8	159,8
2012	50,9	64,4	76,0	84,3	86,2	88,7	119,1
2013	43,8	73,2	94,2	110,5	116,7	116,8	129,9
2014	55,6	77,3	104,9	115,8	122,4	127,4	130,8
2015	40,7	48,7	65,1	69,1	70,9	96,6	111,7
2016	49,7	82,1	94,1	97,4	120,1	129,8	151,2
2017	50,5	65,7	74,9	90,2	131,3	151,4	154,2
2018	60,4	67,8	81,3	88,4	92,1	92,4	123,0
Max.	75,0	95,5	138,7	157,6	162,0	165,1	177,7

La tabla 4 presenta todos los parámetros de dispersión, posición y demás variables necesarias que se requirieron para la función de distribución de probabilidad de Gumbel, para períodos de 2, 5, 10, 25, 30, 50 y 75 años para las duraciones de 1, 2, 4, 6, 8, 12 y 24 horas.

Curvas de intensidad duración y frecuencia (IDF)

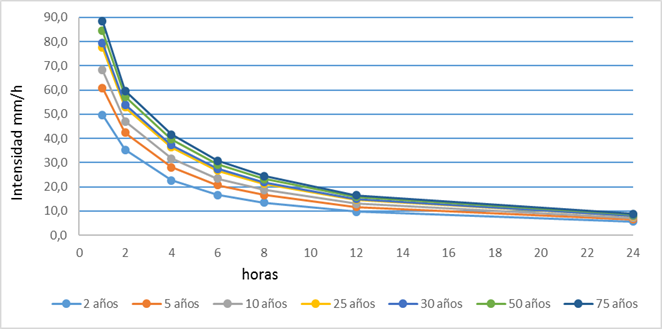
Se estimaron los valores proyectados a periodos de 2, 5, 10, 25, 30, 50 y 75 años aplicando la ecuación (9), con los datos de X y (Sn-1) de la tabla 2 y los de y, k, Dx de la tabla 4. En la figura 4 se exponen los resultados de las curvas IDF para cada periodo de retorno. Aquí se pueden observar intensidades que para 1 h se estiman de 49,7 mm/h. a períodos de 2 años mientras que para 75 años estas alcanzan un valor de 88,6 mm/h. A 24 h para estos períodos se consideran 5,6 y 8,8 mm/h respectivamente. Para duraciones de 2 h los valores sobrepasan los 30 mm/h alcanzando los 60mm/h en 75 años, para 4 h sobrepasan los 20 mm alcanzando los 41 mm a los 75 años. A partir de las duraciones de 6 h los valores se encuentran debajo de los 32 mm/h (75 años) y en la duración de 24 h todos los valores están por debajo de los 10 mm/h.

Tabla 2 Intensidades de precipitación en (mm/h) de Puyo en el período 1987-2018 

Horas Años	1h	2h	4h	6h	8h	12h	24h
1987	40,5	32,8	22,7	17,3	15,2	12,2	6,7
1988	46,1	32,5	24,5	18,3	15,3	10,3	6,7
1989	37,5	33,0	22,2	20,6	15,8	10,7	6,6
1990	60,5	45,8	24,6	16,4	12,6	9,1	7,4
1991	68,9	41,4	23,4	16,6	12,7	10,3	6,2
1992	46,3	34,8	32,6	26,3	20,3	13,8	6,9
1993	33,2	28,3	16,9	11,6	8,7	6,0	3,7
1994	43,5	28,4	16,1	13,0	10,5	8,1	4,4
1995	36,9	25,2	19,3	12,9	9,9	7,8	5,4
1996	39,4	29,1	21,4	17,4	14,1	9,8	5,9
1998	46,7	40,3	30,4	22,4	17,7	12,1	6,2
1999	46,5	29,7	20,6	14,7	11,4	8,1	4,5
2000	38,0	28,3	17,7	17,3	15,0	10,8	5,7
2001	54,0	41,0	30,2	21,7	16,5	11,1	5,7
2002	41,5	29,7	15,1	11,2	8,5	7,6	4,7
2003	52,1	40,9	28,4	19,0	15,1	10,2	5,7
2004	61,6	38,3	19,6	15,3	12,7	10,1	5,6
2005	75,0	47,4	24,6	16,6	12,5	9,4	7,3
2006	59,0	36,3	19,6	13,1	10,3	8,4	4,9
2007	63,7	44,8	34,7	25,2	19,0	13,6	6,8
2008	68,0	44,9	26,4	18,1	14,5	10,0	5,1
2009	63,0	47,8	34,1	24,9	18,8	12,5	6,3
2010	53,7	40,9	28,8	20,1	15,2	10,7	5,9
2011	65,7	47,1	25,8	17,3	15,7	11,2	6,7
2012	50,9	32,2	19,0	14,1	10,8	7,4	5,0
2013	43,8	36,6	23,6	18,4	14,6	9,7	5,4
2014	55,6	38,7	26,2	19,3	15,3	10,6	5,5
2015	40,7	24,4	16,3	11,5	8,9	8,1	4,7
2016	49,7	41,1	23,5	16,2	15,0	10,8	6,3
2017	50,5	32,9	18,7	15,0	16,4	12,6	6,4
2018	60,4	33,9	20,3	14,7	11,5	7,7	5,1
Media (X)	51,4	36,4	23,5	17,3	13,9	10,0	5,8
Desviación estándar (Sn-1)	11,0	6,9	5,4	3,9	3,1	1,9	0,9

Tabla 3 Valores máximos de intensidades para períodos de retorno (mm/h) 

Período de Retorno T	Valor máximo de intensidad en 1 h (mm/h)	Probabilidad Excedencia		Probabilidad no Excedencia
Años		f(x)	%	F(x)	%
2	49,7	0,50	50,00	0,500	50,00
5	60,8	0,200	20,00	0,800	80,00
10	68,2	0,100	10,00	0,900	90,00
25	77,5	0,040	4,00	0,960	96,00
30	79,3	0,033	3,33	0,967	96,67

Tabla 4 Parámetros de dispersión, posición en la función de distribución de probabilidad de Gumbel 

T (tiempo en años)	y	k	Dx
			1 hora	2 horas	4 horas	6 horas	8 horas	12 horas	24 horas
2	0,367	-0,156	-1,71	-1,07	-0,84	-0,62	-0,48	-0,30	-0,14
5	1,500	0,865	9,47	5,94	4,63	3,42	2,68	1,65	0,79
10	2,250	1,541	16,88	10,58	8,25	6,08	4,77	2,94	1,40
25	3,199	2,395	26,23	16,45	12,83	9,46	7,42	4,57	2,18
30	3,384	2,562	28,07	17,60	13,73	10,12	7,93	4,89	2,33
50	3,902	3,029	33,17	20,81	16,22	11,96	9,38	5,78	2,75
75	4,311	3,397	37,21	23,34	18,20	13,41	10,52	6,48	3,09

Figura 4 Curvas de intensidad, duración y frecuencia para diferentes periodos de retorno 

CONCLUSIONES

• El análisis histórico de las intensidades y láminas de precipitación máximas reportadas muestra una tendencia de incremento para las intensidades de 1 h y 2 h, mientras que para 4 h, 6 h, 8 h, 12 h y 24 h no se presentan tendencias crecientes o decrecientes.

• La función de estimación de probabilidad de Gumbel, permitió la proyección de los valores a los diferentes períodos de retorno, donde se estima que los valores de intensidades de lluvia en los diferentes períodos de retorno para duraciones de 1 h puedan alcanzar los 50 mm/h en dos años mientras que a partir de los cinco años sobrepasan los 60 mm/h y alcanzando, a los 75 años, 88,6 mm/h.

• A medida que se incrementan las duraciones horarias, disminuyen las intensidades reportando todas las proyecciones a 24 h valores inferiores a los 10 mm/h.

RECONOCIMIENTO

Un especial agradecimiento a las instituciones que permitieron el desarrollo del presente trabajo como el Instituto Nacional de Meteorología e Hidrología y la Universidad Estatal Amazónica.

REFERENCIAS

Campos D. (2010). “Intensidades máximas de lluvia para diseño hidrológico urbano en la república mexicana”. Ingeniería Investigación y Tecnología vol.11, no.2, pp. 179-188. ISSN: 2594-0732. Universidad Autónoma de México, México.

Chow V., Maindment D. y Mays L. (1994). “Manual de Hidrología Aplicada”. Mc Graw-Hill. ISBN: 0-07-010810-2, Santafé de Bogotá, Colombia.

Darba J. (2006). “La utilización de métodos probabilísticos para la evaluación económica de tecnologías sanitarias”. Gaceta Sanitaria, vol. 20, pp. 74-77, ISSN: 0213-9111, Sociedad Española de Salud Pública y Administración Sanitaria. Barcelona, España.

Gorgas J., Cardie N. & Zamorano J. (2011). “Estadística básica para estudiantes de ciencias”. Universidad Complutense. ISBN: 978-84-691-8981-8. Madrid, España.

Guachamín W., García F., Arteaga M. y Cadena J. (2015). “Determinación de ecuaciones para el cálculo de intensidades máximas de precipitación”. Instituto Nacional de Meteorología e Hidrología. Extraído de: Extraído de: http://www.serviciometeorologico.gob.ec/Publicaciones/Hidrologia/ ESTUDIO_DE_INTENSIDADES_V_FINAL.pdf en marzo 2019.

Martínez Y. y Villalejo V. (2018). “La gestión integrada de los recursos hídricos: una necesidad de estos tiempos”. Ingeniería Hidráulica y Ambiental. vol.39, no.1, pp. 58-72. Universidad Tecnológica de la Habana José Antonio Echeverría (Cujae), ISSN 1815-591X. La Habana, Cuba.. Extraído de: Extraído de: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1680-03382018000100005&lng=es&tlng=es en marzo 2018.

OMM (2014). “Guía de Instrumentos y Métodos de Observación Meteorológicos”. Organización Meteorológica Mundial (OMM), ISBN 978-92-63-36008-3. Génova, Suiza. Extraído de Extraído de https://library.wmo.int/pmb_ged/wmo_8-2014_es.pdf en octubre 2018.

OMM (2015). “Nuevo enfoque de dos niveles para las normales climatológicas”. Extraído de: Extraído de: https://public.wmo.int/es/media/news/nuevo-enfoque-de-dos-niveles-para-las%E2%80%9C normales-climatol%C3%B3gicas%E2%80%9D en diciembre 2018

Pizarro R., Flores J., Sanguesa C. y Martínez E. (2003). “Módulo 2 Curvas Intensidad Duración Frecuencia”. Sociedad Estándares de Ingeniería para Aguas y Suelos Ltda. Talca, Chile. Extraído de: Extraído de: http://ctha.utalca.cl/Docs/pdf/Publicaciones/manuales/b_modulo_IDF.pdf en mayo 2019.

Sánchez J. (2017). “Hidrología Superficial y Subterránea”. Create Space Independent Publishing Platform. ISBN-10: 1975606604, Salamanca, España.

Torregrosa V. (2014). “Diccionario etimológico de meteorología y ciencias afines”. Agencia Estatal de Meteorología (AEMET), España. Extraído de: Extraído de: https://repositorio.aemet.es/handle/20.500.11765/7952 en mayo 2019.

Recibido: 28 de Mayo de 2019; Aprobado: 12 de Noviembre de 2019

Jairo Miguel Maldonado Erazo. Técnico Regional Pastaza, Inst. Nac. de Meteorología e Hidrología, (INAMHI) Pastaza, Ecuador. email: [e-mail]

Jairo Rafael Samaniego Merchán. Profesional independiente, Pastaza, Ecuador. email: [e-mail]

Diego Mauricio Ramos Criollo. Estudiante Universidad Estatal Amazónica, Carrera de Ingeniería Ambiental, Pastaza, Ecuador. email: [e-mail]

Ricardo Vinicio Abril Saltos. Docente Universidad Estatal Amazónica, Carrera de Ingeniería Ambiental, Pastaza, Ecuador. email: [e-mail]