Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Si se analiza la evolución histórica de las técnicas estadísticas se aprecia que cada día estas se han ido transformando a favor de lograr mayor validez en los resultados que se obtienen de las investigaciones de causalidad en las ciencias médicas; es por ello que su perfeccionamiento es un problema de investigación que no pierde vigencia.1,2
El paradigma de búsqueda de relaciones causales persigue encontrar un modelo que explique las relaciones entre las variables de un problema; esto tradicionalmente se ha basado en relaciones probabilísticas simétricas entre las variables, lo cual es de utilidad, ya que una mayor probabilidad implica mayor verosimilitud del efecto, pero no siempre certeza. En el análisis estadístico implicativo, conocido por la sigla ASI (de Analyse Statistique Implicative, del idioma francés, donde se originó), por el contrario, las relaciones se establecen a partir de índices con carácter asimétrico, y admite excepciones en las relaciones causa-efecto.
El ASI es una herramienta de la minería de datos basada en la teoría de la cuasi-implicación, la inteligencia artificial y el álgebra booleana, para modelar la cuasi-implicación entre sujetos y variables de un conjunto de datos.3
En el caso de la investigación de causalidad en salud, ya ha sido identificado y fundamentado el empleo de este análisis.4 El presente estudio expone el diseño de una metodología que permite utilizar eficientemente el ASI en la identificación de factores pronósticos o de riesgo, tal como se hace en las investigaciones de la didáctica de las matemáticas y otros campos, donde este análisis ha sido aplicado satisfactoriamente.
Una vez culminado el análisis, uno de los aspectos álgidos de la metodología para la correcta aplicación del ASI fue la interpretación de los resultados, lo cual se convirtió en la etapa más compleja, lo que reafirma el valor de la metodología creada, si se tiene en cuenta que en casi diez años de trabajo se han ido modificando las ideas acerca de cómo interpretar los resultados, a partir de la experiencia adquirida en cada uno de los diferentes estudios realizados en la Universidad de Ciencias Médicas de Santiago de Cuba, bajo la dirección de la Dra. C. Zamora.5,6,7,8,9,10,11
El objetivo de este trabajo es describir los métodos y procedimientos empleados para la interpretación de los resultados del ASI.
Desarrollo
Estos métodos para la interpretación tienen como referentes teóricos lo recogido por la literatura, y como prácticos, los estudios antes comentados.
A continuación, se presentan las interpretaciones que se consideran (por las autoras) más apropiadas hasta el momento, las cuales son susceptibles de modificación, a la luz de los nuevos conocimientos.
Interpretación de los resultados del ASI
La interpretación de los resultados del ASI se ha hecho sobre los índices, las tablas y los tres gráficos que brinda el sistema, a partir de los que se identifican los posibles factores causales, las variables confusoras, las modificadoras del efecto y otras intervinientes, conformando cuatro subetapas que se corresponden con las subetapas del procesamiento y análisis de los datos en la metodología diseñada.
Interpretación de tablas e índices
Según la metodología se interpretarán las frecuencias absolutas y relativas más relevantes en cada grupo de estudio, destacando las características que predominen y los indicadores estimados para cada variable como sus medias, desviaciones estándares, frecuencias de ocurrencias de cada par de variables, coeficientes de correlación, los índices de similaridad, de cohesión implicativa y de implicación inclusión, las tipicalidades y contribuciones de los individuos.
Se distinguen para su interpretación los indicadores propios de este análisis:
El índice de similaridad de Lerman, que no es más que la probabilidad de que el número observado de copresencias entre dos variables sea mayor o igual que el de las copresencias esperadas por el azar.
El índice de implicación, indicador de la no implicación de a sobre b.
La intensidad implicativa, medida probabilística de la validez de la regla, que compara la cantidad de contraejemplos esperados por el azar con los observados. La decisión de aceptar o no la regla está en función del nivel de confianza elegido por el investigador.
La intensidad de implicación-inclusión o intensidad entrópica, versión entrópica de la intensidad implicativa que supera la poca discriminación de esta en muestras grandes. Mide tanto la fuerza de la implicación como la de su negación.
El índice de cohesión entre dos variables a y b o clases de variables, que mide la fuerza de la relación de las variables involucradas en la clase creada.
El resto de los índices a interpretar no se definen aquí, porque forman parte de la Estadística clásica.
Interpretación del árbol de similaridad
En el árbol de similaridad aparecerán agrupados aquellos factores que reúnan características similares, atendiendo a la medida de similaridad definida. Asociadas a estos grupos pueden estar o no las variables dependientes definidas, de forma tal que:
Si la variable dependiente ‘vivo’ (‘fallecido’) aparece como miembro de un conglomerado de factores, estos factores se interpretan como los predominantes para la condición de vivo (fallecido).
Si las variables dependientes no resultan ser miembros de ningún conglomerado de factores, esta situación se interpretaría en el sentido de que no existe similitud entre ellos.
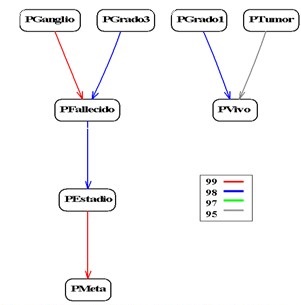
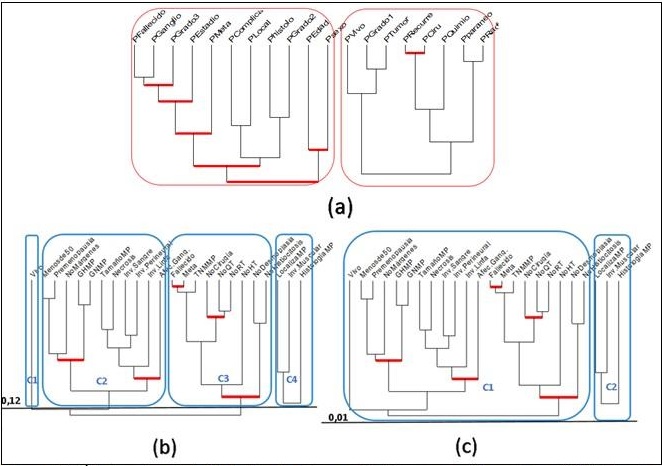
Estudios referidos a la utilidad del análisis estadístico implicativo para la identificación de factores pronósticos de mortalidad por cáncer,6 y de factores pronósticos del cáncer de mama,11 ilustran sus resultados mediante árboles de similaridad (Figura 1). En el de Moraga Rodríguez y colaboradores (1a),6 se aprecia la formación de dos grandes grupos, uno que incluye la variable PFallecido y a un grupo de factores como las metástasis (PMeta), las complicaciones (PComplica), la edad avanzada (PEdad), el estadio avanzado (PEstadio), entre otros, interpretándose que estos factores predominan entre los fallecidos. Del segundo grupo se puede concluir que el grado menor de diferenciación del tumor (PGrado1), el mayor tamaño tumoral (PTumor), los tratamientos con cirugía (PCiru), la radioterapia (PRadio) y la quimioterapia (PQuimio), fueron los factores más frecuentes entre los vivos (PVivo).
La formación de los grupos o conglomerados dependerá del nivel escogido por el investigador como significativo para poder considerar la existencia de similitud entre sus miembros; así, por ejemplo, Pardo Santana y colabores11 consideraron un índice de similaridad de 0,12, donde se forman cuatro clases, y queda el vivo no asociado a ningún factor (1b); si hubieran considerado el nivel mínimo, se tendrían dos clases donde se unen vivos y fallecidos (1c).
Fuente: Moraga Rodríguez y colaboradores (2016); Pardo Santana (2019)Fig. 1 - Árboles de similaridad.
Interpretación del grafo implicativo
Esta subetapa conlleva la interpretación de tres grafos implicativos, y dentro de ellos se tendrán en cuenta procedimientos, como se describe a continuación:
En el grafo implicativo normal:
En los dos grafos implicativos en modo cono, identificar:
Posibles factores causales:
Relaciones mutuas
Posibles variables confusoras
Posibles variables intervinientes
Posibles variables colisionadoras
La interpretación se basó en la similitud estructural del grafo implicativo con un grafo acíclico orientado, conocido como DAG (del inglés Directed Acyclic Graph), diagrama causal que plantea posibles rutas de asociación entre causas y efecto, así como otras rutas alternativas generadoras de sesgos, por lo que facilitan también el control de estos. Además, guían al investigador en cuanto a cuáles variables deben incluirse en el análisis.12-15
Sagaró y Zamora16 describen las categorías y elementos básicos a tener en cuenta en un DAG, así como los tres modos en que pueden establecerse las relaciones entre dos variables (X e Y), ajustando por una tercera (Z):
Reconocimiento del conjunto de relaciones multivariadas
En el grafo implicativo normal es posible observar las relaciones que se establecen entre todo el conjunto de variables definidas, así como la intensidad y el sentido de cada implicación. Por ejemplo, en el ya citado estudio Moraga y colaboradores,6 figura un grafo implicativo donde se aprecia que un grado histológico I (PGrado1) implicó estar vivo, con una probabilidad de certeza (intensidad implicativa) igual o superior al 98 %; además, un grado histológico III (PGrado3) y la presencia de ganglios (PGanglio) implicaron haber fallecido, con una probabilidad de certeza igual o superior al 98 % y 99 %, respectivamente. (Figura 2).
Determinación de la intensidad de las relaciones
Al realizar la interpretación del grafo implicativo, se debe mencionar el nivel de confianza o probabilidad de certeza al cual ocurre la relación que se describe. En dependencia del grado de detalle que se desee dar en el informe, se pueden describir solo las implicaciones de mayor intensidad, y el resto quedará visible a través del gráfico, por lo cual se insiste en que se expongan en el acápite de ‘métodos’ los nombres con que se procesarán las variables.
Identificación de los posibles factores causales
Sin dudas, el modo cono del grafo implicativo resulta el más informativo para el objetivo que se persigue, ya que la identificación de los factores causales se hará a través de estos, seleccionando como cono las variables de respuesta D1 (desenlace desfavorable), o D0 (desenlace favorable). Se tomarán en cuenta todos los factores que queden seleccionados con cierta intensidad de implicación, y su interpretación dependerá del tipo de estudio que se realice. Así, en un estudio de factores de riesgo, el modo cono permite identificar los factores de riesgo cuando en el cono del gráfico se coloca la variable ‘enfermo’, y los factores protectores, cuando se sitúa la variable ‘sano´; mientras que en un estudio de factores pronósticos se identifican los factores de buen pronóstico cuando en el cono del gráfico se ubica el evento final favorable, por ejemplo, ‘vivo’, y los factores de mal pronóstico cuando se ubica el evento final desfavorable, por ejemplo ‘fallecido’.
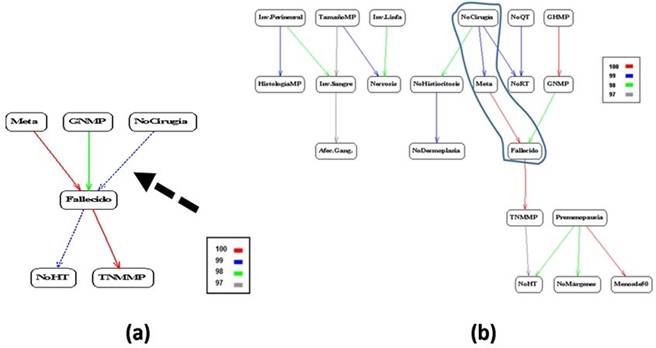
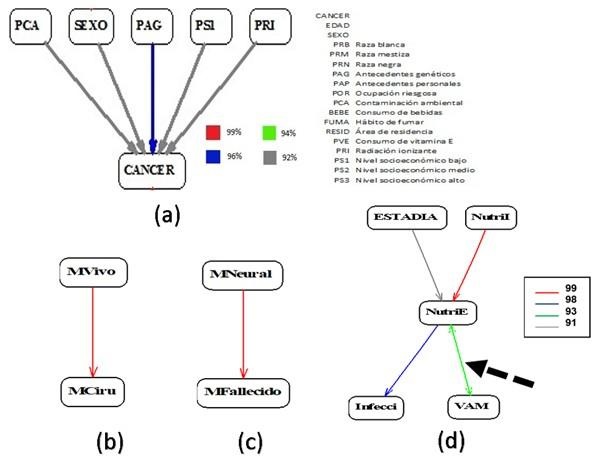
En el estudio de García Mederos y colaboradores,5 el cono del grafo implicativo para la identificación de factores de riesgo del cáncer de pulmón, está representado por la variable que identifica tener cáncer (CANCER), de manera que las variables que aparecen unidas al cono por flechas se consideran los factores de riesgo asociados al cáncer: la contaminación ambiental (PCA), el sexo (SEXO), los antecedentes genéticos (PAG), el nivel socioeconómico bajo (PS1) y la radiación ionizante (PRI) (3a). (Figura 3) Moraga y colaboradores,7 muestran otro grafo implicativo (3b) que permite identificar que, recibir tratamiento quirúrgico (MCiru) es un factor de buen pronóstico, porque se asocia con el evento favorable, que es estar vivo (MVivo). De igual forma, otro grafo implicativo (3c) permite identificar que la invasión perineural (MNeural) es un factor de mal pronóstico, porque se asocia con el evento desfavorable fallecer (MFallecido). (Figura 3).
Fuente: García Mederos y colaboradores (2015), Moraga Rodríguez y colaboradores (2017) y Paez Candelaria y colaboradores (2018)Fig. 3 - Grafos implicativos en modo cono
Identificación de relaciones mutuas
La presencia de enlaces con flechas en ambas direcciones (doble saeta) indica una doble implicación (Figura 3), como se aprecia en el estudio de Paez Candelaria y colaboradores,9 para la identificación de factores pronósticos de malnutrición al egreso del paciente grave, donde la ventilación aérea mecánica (VAM) implicó tener una malnutrición al egreso (NutriE), y a su vez, tener malnutrición al egreso implicó haber recibido este tipo de ventilación, o sea, existe una relación recíproca entre estas variables (3c).
Este tipo de enlace bidireccional puede ser interpretado también como la existencia de un factor confusor, lo cual se comprueba si, al ajustar por el supuesto factor, desaparece el enlace.
Identificación de posibles variables confusoras (sesgo de confusión)
El sesgo de confusión se produce cuando la medición del efecto de una exposición sobre un evento se modifica, debido a la asociación de la exposición con otro factor que influye en el evento. Este sesgo puede conducir a sobreestimar, subestimar, o incluso, revertir el sentido del efecto. Se puede prevenir en la etapa del diseño o controlar en la etapa del análisis, mediante la aplicación de estrategias estadísticas para obtener una estimación no distorsionada sobre el efecto.17
En el diseño se emplea la aleatorización, lo cual posibilita que las variables de confusión conocidas y, lo mejor, desconocidas, se distribuyan de manera homogénea entre los dos grupos, y cuando no sea posible aleatorizar se trata de restringir los criterios de inclusión en función de la variable confusora, o parear en función de ella.
En el análisis se usan medidas de asociación ajustadas, la estratificación o las técnicas multivariadas. Para que se produzca un sesgo de confusión se requiere que esta variable se asocie a la exposición en estudio, pero no como resultado de esta, y se asocie al evento en ausencia de la exposición en estudio.17
En un análisis tradicional para identificar una variable confusora se debe comparar el valor del efecto crudo (riesgo relativo u odds ratio) con el ajustado mediante estratificación aplicando modelos de regresión logística, y si se obtiene una diferencia ≥10-15 %, se considera que existe confusión.17
Este sesgo afecta a todos los estudios observacionales, por ello es frecuente en la investigación clínica cuando no se tiene el control sobre la(s) variable(s) que se miden en los sujetos en estudio, o bien los eventos han ocurrido libremente sin que exista participación alguna del investigador en su ocurrencia.18
Molina19 plantea que se produce confusión cuando la asociación entre la exposición y el efecto puede ser explicada por una tercera variable (variable confusora), o cuando una asociación real queda enmascarada por la variable confusora. Solo es una variable confusora si es factor pronóstico del efecto, se asocia a la exposición y no está incluida en la cadena de producción entre exposición y efecto.
Según un diagrama causal, una confusión se produce cuando una relación A ⇒C cambia por la presencia de una tercera variable. En este diagrama se puede apreciar que los enlaces parten desde la variable confusora (B) (asociada a la causa y al efecto), hacia la causa (A) y hacia el efecto (C), observándose la relación ‘A B⇒C’. Si no se ajusta el análisis por B, entonces la ruta entre A y C permanece abierta y se produce el sesgo de confusión, al encontrarse asociación entre ellas. Esto equivale, en teoría de grafos, a una división, camino de puerta trasera o vía no causal. Si se ajusta por B la ruta queda bloqueada y no aparecerá asociación entre A y C.20,21
En el control de confusión se evalúa la existencia de vías no casuales o “caminos de puerta trasera” abiertos que puedan transmitir una asociación espuria que sesgue la estimación de la asociación. Se buscará el ajuste por esa causa común que “cierra” todos los posibles caminos no causales entre la exposición y el evento.
En este trabajo se propone identificar la existencia de confusión a través del grafo implicativo en dos casos por los siguientes mecanismos:
La presencia de dos nodos adyacentes unidos por un enlace bidireccional: según la teoría de grafos un enlace bidireccional se debe a la existencia de una variable adicional (variable de confusión) con enlaces dirigidos hacia las variables del factor de confusión.22 Estas variables del factor de confusión son los supuestos causa y efecto de la relación encontrada.22 Para corroborar si se trata de una confusión se debe ajustar el análisis por esta variable. Si una vez ajustada por la tercera variable se mantiene el enlace bidireccional, entonces hay causación recíproca.23
Por ejemplo, en la figura 3d se establece una relación bidireccional entre la ventilación mecánica y la malnutrición al egreso; esta puede darse si el investigador no tuvo en cuenta una tercera variable que es la verdadera causa de ambos fenómenos, como es el caso de un estado infeccioso grave que condiciona la malnutrición y la necesidad de ventilación mecánica a la vez.
Un cambio significativo (superior al 10 %) en la intensidad implicativa, es el análisis al incluir o no la supuesta variable confusora, tomando como referente que es posible detectar una variable confusora durante el análisis si se obtiene una diferencia relativa en el efecto mayor del 10 %.17,24,25
Se propone, además, una tercera vía de identificación a través del árbol cohesitivo que se explica más adelante.
En general, cualquier relación del tipo A ⇒C, o A C, puede desaparecer o tornarse de poco interés si aparece una variable B, verdadera causa de C, que influye además en A. Las autoras coinciden con Bacallao24 cuando este plantea que es tarea del investigador la identificación de variables confusoras, a partir del conocimiento teórico específico del problema que origina la evaluación de la posible relación causal.
Identificación de posibles variables intervinientes
Las variables intervinientes o intermedias (B) son aquellas que median entre la causa (A) y el efecto (C), condicionando una relación causa-efecto indirecta (A ⇒ B ⇒ C). La variable intermedia es un paso intermedio por el que se produce el efecto, por ejemplo, la obesidad a través de la hipertensión o la arterioesclerosis, producen el infarto agudo del miocardio.
De la teoría de grafo se dice que una variable entre la causa y el efecto produce un bloqueo o una ‘d-separación’ en el gráfico. Este tipo de relación es llamada cadena o camino causal dirigido. En ella se observará que los enlaces siguen una sola dirección de la causa al efecto.22
En un grafo implicativo en modo cono no solo se presentan relaciones mediante trazos continuos como los que aparecen en las figuras anteriores, también se pueden presentar trazos discontinuos. La presencia de líneas discontinuas expresa que la relación entre los factores implicados no es directa, sino que existen una o más variables intermedias que influyen en el desenlace (cadena causal).
Por ejemplo, en el grafo de la figura 4a (Figura 4) se aprecia que el no haberse operado (NoCirugía) incide en el fallecido a través de otra u otras variables que deben explorarse en el grafo implicativo normal (4b), o sea, que el no haberse operado es causa indirecta del desenlace. En este caso la metástasis es una variable intermedia, entonces la cadena causal sería: no operarse conllevó a tener metástasis, y esto, a fallecer.
Estas variables pueden ser clasificadas como causas cuasi componentes, explicadas más adelante. Es importante no confundirlas con la variable confusora, verdadera causa del efecto. Tampoco se debe confundir con una variable colisionadora.
Identificación de posibles variables colisionadoras (sesgo de selección)
El sesgo de selección ocurre cuando la población seleccionada para participar en el estudio no es representativa de la población de referencia, y en caso de dos o más grupos en comparación, si estos no son similares en sus características basales debido a la forma en que han sido seleccionados.
Este sesgo ocurre con mayor frecuencia en series de casos retrospectivas, estudios de casos y controles, de corte transversal y de aplicación de encuestas, ya que eventos ocurridos en el pasado pueden influir en la probabilidad de ser seleccionados, y conduce a una estimación del efecto diferente del esperado para la población objeto de estudio.17
Molina19 expone los principales errores en los criterios de inclusión o exclusión, o en la sistemática de reclutamiento, conducentes a seleccionar una muestra no representativa de la población, como:
Selección incorrecta de los grupos de estudio: los grupos comparados solo deberían diferenciarse en el factor evaluado. Esta comparabilidad se consigue en los estudios experimentales con la aleatorización, por lo que los estudios observacionales son más susceptibles a este tipo de sesgos.
Pérdidas durante el seguimiento: cuando los que se pierden son sistemáticamente diferentes de los que no lo hacen, en variables relacionadas con el factor de estudio o la variable respuesta (pérdidas informativas).
Ausencia de respuesta: propio de las encuestas transversales. Hay que saber si los que no contestan, difieren de los que sí lo hacen.
Supervivencia selectiva: cuando se seleccionan casos prevalentes en lugar de incidentes. Es típico de los casos y controles, en los que los casos más graves o más leves están infrarrepresentados por fallecer o por curación.
Sesgo de autoselección por participación de voluntarios: existe riesgo de que estos individuos tengan características diferentes a los no voluntarios.
Los errores de selección pueden ser originados por el investigador o como resultado de relaciones complejas en la población en estudio no evidentes para el investigador, como cualquier factor que influya sobre la posibilidad de los sujetos seleccionados de participar o permanecer en el estudio y que, además, esté relacionado con la exposición o con el evento en estudio.18
En un diagrama causal una variable colisionadora (collider del inglés) es llamada así por el choque que se produce sobre ella en el análisis a partir de los enlaces que parten de dos variables (A) y (C), no asociadas casualmente: ‘A⇒B C’. Se dice que el colisionador bloquea el camino. Este tipo de relación es llamada, según la teoría de grafos, colisión, división invertida, camino de choque o colisionador, o estructura en ‘V’.22
Este tipo de variable será una consecuencia común de otras dos variables no asociadas causalmente, al contrario de una confusora, que es causa común de la causa y el efecto.
Este tipo de variable se puede distinguir en el grafo implicativo, tanto en el normal como en el modo cono, cuando se observa una estructura en ‘V’. Por ejemplo, en la figura 3d, se observa que la mala nutrición al ingreso (NutriI) y la estadía prolongada (ESTADÍA) conducen a la mala nutrición al egreso (NutriE). En este caso, seleccionando solo enfermos malnutridos al egreso (no incluyendo la variable NutriE), se produce una falsa asociación entre NutriI y ESTADÍA, con una intensidad implicativa igual a 85, denominada sesgo de selección, ya que se debe a la selección incorrecta de los sujetos del estudio. Este sesgo también es llamado sesgo del collider.
Si se compara el grafo implicativo con un grafo acíclico dirigido se puede apreciar que ambos permiten identificar los factores que influyen sobre un desenlace, pero el segundo no permite identificar si influyen a favor o en contra de este, y tampoco dan información sobre la magnitud del efecto. Sin embargo, mediante el grafo implicativo en modo cono se puede reconocer cuando un factor es protector o de riesgo y, además, el nivel de intensidad de todas las implicaciones.
Interpretación del árbol cohesitivo
Para la interpretación del árbol cohesitivo se tendrán en cuenta los siguientes aspectos:
Interpretación de las reglas obtenidas según el enfoque.
Clasificación de las causas.
Identificación de posibles variables confusoras.
Identificación de la interacción.
Identificación de los sujetos típicos y contributivos.
1) Interpretación de las reglas obtenidas según el enfoque
Para interpretar el árbol cohesitivo se considerarán dos enfoques:
Del factor (F) causal al desenlace (Di), esto es, cuando el desenlace es cuasi-implicado por un factor y se denota por «F ⇒ Di».
Del desenlace al factor causal, esto es, cuando el factor es cuasi-implicado por el desenlace y se denota por «Di⇒ F»
Al interpretar las reglas que se forman, y siguiendo la interpretación dada en el campo de la Didáctica, por Gras,26 el primer enfoque se interpretará como: “cuando el factor está presente entonces usualmente se produce el desenlace”; y el segundo, como: “existieron muy pocos individuos en los que se produjo el desenlace que no presentaban el factor”.
Para una interpretación de mayor complejidad se propone, además, la clasificación de las causas.
2) Clasificación de las causas
Teniendo en cuenta el modelo de Rothman27,28y la terminología cuasi-implicativa, se han creado cuatro tipos de causas: cuasi-componentes, cuasi-suficiente, cuasi-necesaria y cuasi-equivalente (cuasi-suficiente y cuasi-necesaria a la vez), las cuales se explican a continuación. Estos tipos de causas se identifican básicamente a partir de las reglas obtenidas del árbol cohesitivo.
Causas cuasi-componentes
No existe un único factor que pueda constituirse como causa cuasi-componente de un desenlace, debido a ello se define como causas cuasi-componentes a los factores que forman parte de una regla (R) o meta regla (R*) entre factores, que se relacionen directamente con el desenlace, estando este último cuasi-implicado por R o R*, donde: R puede ser del tipo: F*⇒ F, F* F o F* F; y R*puede ser del tipo: F*⇒ R, F* R o F* R; siendo F y F* las causas cuasi-componentes.
Por ejemplo, como se observa en la figura (Figura 5), para la identificación de factores pronósticos de mortalidad en el cáncer de próstata, la regla R2: (PrMeta⇒ Ganglio) es del tipo F*⇒ F, (5a, modificado de Moraga8) lo cual significa que tener metástasis implicó, con cierto índice de cohesión, tener afectación ganglionar, por lo que se puede decir que la presencia de metástasis y afectación ganglionar son causas cuasi-componentes de mal pronóstico en el cáncer de próstata. También son causas cuasi-componentes los factores presentes en R1 (del tipo F* F), R3 (R2⇒ R1) y R4 (F* ⇒ R).
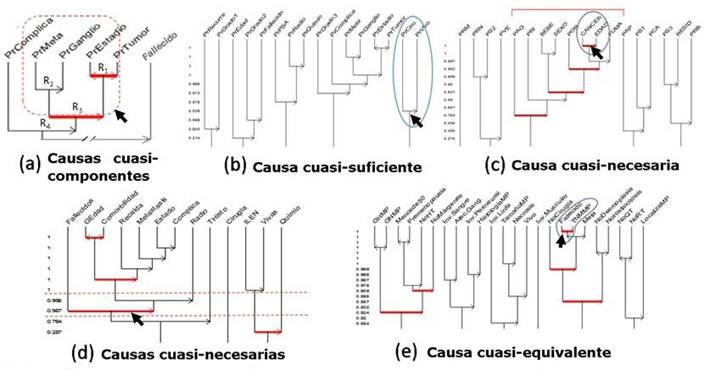Fuente: Modificado de Moraga Rodríguez (2018), García Mederos (2015), Lambert 92017) y Pardo Santana (2019)Fig. 5 - Árboles cohesitivos.
Las variables antes mencionadas como intervinientes o intermedias podrán ser clasificadas como causas cuasi componentes.
Causa cuasi-suficiente
La causa cuasi-suficiente es el conjunto formado por las causas cuasi-componentes. En el caso particular de que exista un factor que implique directamente al desenlace (F*⇒D), este constituirá una causa cuasi-suficiente, situación que se presenta muy pocas veces. Por ejemplo, en la regla R8: (PrCiru⇒PrVivo), del estudio de Moraga,8 la cual se interpreta de la siguiente forma: “casi todos los individuos operados siguieron con vida”, con un índice de cohesión de 0,836, “operarse es cuasi-suficiente para estar vivo” (figura 5b). Esta interpretación puede también ser expresada de otras formas: “la cirugía predispone al paciente al evento favorable” o “la casi totalidad de los pacientes que se operan se mantienen vivos”. Esto quizás sea debido a la indicación de la cirugía en los primeros estadios de la enfermedad, pero esta explicación formaría parte de la discusión de los hallazgos del estudio, lo cual no representa un objetivo de esta investigación.
Entre las causas cuasi-componentes que forman una causa cuasi-suficiente existe una interacción biológica que puede depender de otras causas cuasi-componentes, de manera que el hallazgo de una regla de este tipo será el punto de partida de otro análisis para probar la hipótesis de interacción encontrada en dicha regla.
Causa cuasi-necesaria
Se dirá que el factor F* es una causa cuasi-necesaria cuando se relaciona con el desenlace y está cuasi implicado por este (D ⇒ F*). También se denomina causa cuasi-necesaria al conjunto formado por todos los factores que integran reglas o meta-reglas que estén relacionadas con el desenlace, y estén cuasi implicadas por este.
Por ejemplo, en la regla R1: (CANCER ⇒ EDAD) del estudio de García5 (figura 5c), la cual se interpreta de la siguiente forma: “tener cáncer implicó siempre (con un índice de cohesión de 1) tener una edad avanzada”; la edad avanzada es una causa cuasi-necesaria para tener cáncer de pulmón, o sea, que deben estar presentes otros factores coincidiendo en el individuo para que este desarrolle cáncer de pulmón.
En la figura 5d, tomada de la tesis de especialidad en Bioestadística del Lic. Yuber Lambert,[a] se ejemplifica el caso de un conjunto de causas cuasi-necesarias, en el cual el desenlace (Fallecidos) cuasi implica una metarregla R**, esto es, Fallecidos ⇒ R**, donde:
Causa cuasi-equivalente
Se dirá que el factor F* es una causa cuasi-equivalente si es cuasi-necesaria y cuasi-suficiente a la vez, o sea, si este factor cuasi implica, y está cuasi implicado por el desenlace (D ⇔ F*).
En la figura 5e se presenta la regla R1: (Fallecido ⇔ TNMMP) del estudio de Pardo, antes mencionado. La interpretación que se hace de esta regla es la siguiente: “fallecer implicó siempre tener un estadio avanzado de la enfermedad (TNMMP), y tener un estadio avanzado de la enfermedad implicó siempre fallecer (con un índice de cohesión igual a 1)”.
3) Identificación de posibles variables confusoras
Mediante el árbol cohesitivo se obtiene una tercera vía para la identificación de variables confusoras cuando se obtienen reglas absurdas. Cuando aparecen relaciones entre variables cuya asociación directa no tiene sentido desde el punto de vista médico, se puede pensar en la existencia de una variable confusora, que no se tuvo en cuenta en el diseño del estudio. Por ejemplo, en un estudio de factores de riesgo del bajo peso al nacer se puede hallar que la escolaridad materna es un factor de riesgo si no se recogen datos sobre la edad materna, ya que podría haber muchas adolescentes que aún no alcanzan el preuniversitario, entonces la edad materna debe ser el verdadero factor de riesgo no controlado que está influyendo sobre la escolaridad y el bajo peso al nacer. Como es conocido, a menos que sea posible ajustar el efecto de confusión de esta tercera variable, sus efectos no pueden distinguirse de los de un factor de riesgo o pronóstico en estudio.
4) Identificación de la interacción
Existe interacción o modificación del efecto cuando la asociación entre exposición y efecto varía según las categorías de una tercera variable, la variable modificadora de efecto.
Tomando como referentes a Hernán y Robins29 y Hallqvist,30 autores que consideran útil el modelo de Rothman para descubrir la interacción, al considerar que dos causas componentes de una causa suficiente única tienen una interacción mutua y que el grado de interacción depende de la prevalencia de los otros factores que la integren, se ha considerado la posible interacción entre las denominadas causas cuasi-componentes, lo cual debe ser confirmado en cada estudio por el investigador experto, que en ese caso incluirá el término de interacción en el modelo de regresión logística que se haga posteriormente.
Estas variables se describen e interpretan sin necesidad de controlarlas, como ocurre con las variables confusoras, ya que las modificadoras de efecto reflejan una característica de la relación entre exposición y efecto, cuya intensidad depende de esta variable. No tiene sentido calcular una medida ajustada, ya que no sería representativa de la asociación global entre exposición y efecto, y tampoco tendría sentido estratificar y hacer una media entre los estratos.
5) Identificación de los sujetos típicos y contributivos
La determinación cuantitativa de los sujetos responsables de las estructuras formadas en los árboles cohesitivo y de similaridad viene dada por su contribución y/o su tipicalidad. La tipicalidad es un índice porcentual que mide cómo se comporta un individuo en relación a la regla, llamando sujeto típico a aquel que verifica todas las implicaciones que poseen mayor intensidad de implicación en la formación de las clases. La contribución cuantifica el aporte de un determinado individuo en la formación de la regla. Por ejemplo, si una regla: a ⇒ b posee una intensidad implicativa de 0,7, entonces los individuos más contributivos son los que tienen el valor 1 para las variables a y b.
Las interpretaciones del grafo implicativo y las reglas obtenidas a partir del árbol cohesitivo deben corresponderse siempre. La determinación de cuál de estos factores es predisponente, facilitador, desencadenante, potenciador, etc., queda fuera de las relaciones estadísticas, y deben ser determinadas por el experto. Las interpretaciones presentadas tampoco contradicen los indicadores relacionados con la exposición al factor, ni algún análisis que se haga a posteriori en base a los criterios de causalidad establecidos por diferentes autores, como los de Bradford Hill o algún algoritmo empleado, por ejemplo, para la identificación de las reacciones adversas en farmacovigilancia.
Cambios evolutivos en la interpretación de los resultados del ASI
Como se planteó antes, la interpretación en estos trabajos ha ido evolucionando conforme a los métodos empleados en el análisis; así, en los tres primeros estudios realizados, donde se identificaron los factores de riesgo de los cánceres de mama, pulmón y próstata, se identificaron los factores de riesgo a partir del grafo implicativo normal.5 Sin embargo, en los seis estudios siguientes para la identificación de los factores pronósticos de estos mismos tipos de cánceres, el reconocimiento de los factores pronósticos se hizo a partir del modo cono del grafo implicativo, y se pudieron identificar los factores de buen pronóstico a partir de la duplicación de la variable dependiente.6-11
En los últimos estudios en fase de publicación, se reconoce, además, la diferencia entre los posibles factores causales directos e indirectos, y se aplican todas las categorías expuestas en este trabajo.
Conclusiones
En este trabajo se proponen, para la interpretación de los resultados de la aplicación del análisis estadístico implicativo en los estudios de causalidad en salud, los criterios que hasta el momento parecen más plausibles a las autoras, lo que no está exento de cambios a la luz de nuevos conocimientos o la experiencia de otros investigadores.
