APLICACIÓN DE LA COMPUTACION

 

Análisis y optimización de una celda de combustible de membrana de intercambio protónico

 

Analysis and optimization of a proton exchange membrane fuel cell using modeling techniques

 

 

Ing. Raciel de la Torre Valdés, MSc. Lázaro Roger García Parra y MSc. Daniel González Rodríguez

Facultad de Ciencias y Tecnologías Nucleares, Instituto Superior de Tecnologías y Ciencias Aplicadas, InSTEC, La Habana, Cuba.

 

 

---

RESUMEN

En el presente trabajo se realizó la modelación tridimensional y estacionaria de una celda de combustible de intercambio protónico empleando técnicas de modelación de dinámica de fluidos computacional, específicamente el software ANSYS FLUENT 14.5. El modelo fue comparado con datos experimentales y con resultados de otro modelo. Se analizaron los parámetros de operación del dispositivo presión y temperatura, sentido de los flujos, porosidad de los electrodos, humidificación de los gases y concentración de oxígeno. Se optimizó el diseño de la celda teniendo en cuenta las dimensiones de los canales y el espesor de la membrana. Se analizó el rendimiento de la celda funcionando con la membrana SPEEK (por sus siglas en inglés). Para realizar este estudio fue necesario modificar la expresión que describe la conductividad iónica. Se encontró que el rendimiento del dispositivo tiene gran sensibilidad a la variación de los parámetros termodinámicos y la composición de los gases.

Palabras clave: dinámica de fluidos computacional, hidrógeno, membrana de intercambio protónico, modelación de celdas de combustible.

---

ABSTRACT

This paper proposes a three-dimensional, non-isothermal and steady-state model of Proton Exchange Membrane Fuel Cell using Computational Fluid Dynamic techniques, specifically ANSYS FLUENT 14.5. It's considered multicomponent diffusion and two-phasic flow. The model was compared with experimental published data and with another model. The operation parameters: reactants pressure and temperature, gases flow direction, gas diffusion layer and catalyst layer porosity, reactants humidification and oxygen concentration are analyzed. The model allows the fuel cell design optimization taking in consideration the channels dimensions, the channels length and the membrane thickness. Furthermore, fuel cell performance is analyzed working with SPEEK membrane, an alternative electrolyte to Nafion. In order to carry on membrane material study, it's necessary to modify the expression that describes the electrolyte ionic conductivity. It's found that the device performance has got a great sensibility to pressure, temperature, reactant humidification and oxygen concentration variations.

Key words: computational fluid dynamics, hydrogen, polymeric electrolyte membrane, fuel cell modeling.

---

 

 

INTRODUCCIÓN

En la actualidad se ha impulsado el interés y desarrollo de algunas fuentes energéticas alternativas. En el sector del transporte la utilización del hidrógeno como vector energético se presenta con buenas perspectivas de aplicación.

Las celdas de combustible de membrana de intercambio protónico (PEMFC) ofrecen eficiencias inigualables por otras tecnologías de generación eléctrica y el único producto del proceso es agua [1]. Estas celdas están compuestas por dos colectores de corriente, dos electrodos, dos capas de catalizador y un electrolito, como muestra la figura 1.

Estos dispositivos todavía no son competitivos debido a su alto precio. Por este motivo actualmente se investigan materiales alternativos de más bajo costo que ofrezcan rendimientos aceptables y que permitan ampliar el rango de la temperatura de operación. El costo de las celdas PEM también puede reducirse optimizando su funcionamiento. La modelación computacional de estos dispositivos permite analizar cada uno de los parámetros de operación y de diseño con un costo relativamente bajo. Los software de Dinámica de Fluidos Computacional (CFD) permiten realizar análisis en los que se consideran las ecuaciones de conservación de la masa, del momento y de la energía, las ecuaciones que caracterizan la reacción electroquímica y las que describen el comportamiento de los fluidos. En este trabajo se empleó la herramienta ANSYS FLUENT 14.5. La modelación del dispositivo se realizó con el objetivo de analizar el efecto que tienen en el funcionamiento de la celda, la variación de parámetros como la presión y la temperatura, el sentido de los flujos de gases, la porosidad de los electrodos, la humidificación de los gases y la concentración de oxígeno. Se optimizó el diseño del dispositivo teniendo en cuenta las dimensiones de los canales y el espesor de la membrana. Como análisis novedoso de este trabajo se destaca el estudio de la influencia del material de la membrana en el funcionamiento del dispositivo.

 

MATERIALES Y MÉTODOS

La diferencia de potencial entre el colector catódico y la interfaz electrolito/electrodo, en la cual se ubica el catalizador, es la que provoca el movimiento de electrones a través del circuito. La transferencia volumétrica de corriente (I) se define según la formulación de Butler-Volmer, simplificada según Tafel como muestran las ecuaciones (1) y (2), [2].

Donde:
I: Transferencia volumétrica de corriente,
ξ: Área de la superficie activa,
j^ref: Variación de densidad de corriente por área de superficie activa de referencia,
X: es la concentración molar de especies,
X_ref : Valor de referencia de la concentración molar,
Υ:Exponente de dependencia de concentración,
α: Coeficiente de transferencia de carga,
η: Pérdida por activación,
F: Constante de Faraday,
R: Constante universal de los gases y
T: Temperatura de operación.

En la ecuación (1), se muestran las variables correspondientes a la región del ánodo y en la ecuación (2) las correspondientes a la región del cátodo.

La pérdida de activación (η) se define entre los potenciales del colector (V_celda) y de la membrana, ecuaciones (3) y (4). La ganancia en el potencial eléctrico por el paso desde el ánodo hasta el cátodo puede considerarse teniendo en cuenta el voltaje de circuito abierto (V_OC) en el cátodo [2].

Donde:
Vcelda: Voltaje de operación de la celda,
φ_mem: Potencial eléctrico en la región de la membrana,
V_OC: Voltaje de circuito abierto

El voltaje de circuito abierto puede ser calculado empleando la ecuación (5), [3].

Conductividad iónica del electrolito

La conductividad iónica del electrolito depende del contenido de agua que exista en esta región. Por lo tanto, es necesario calcular determinados parámetros, como la actividad del agua y los mecanismos de difusión del agua en la membrana para describir el funcionamiento de la celda. La conductividad iónica (σ) del Nafion 117 en función del contenido de agua (λ) ha sido obtenida por otros autores a una temperatura de 303 K [4], permitiendo obtener las ecuaciones (6) y (7).

Donde:
σ:Conductividad eléctrica de la membrana,
σ_{(303 K)}: Conductividad eléctrica de la membrana a 303 K y
λ: Contenido de agua de la membrana.

En la ecuación (7), el factor e^{[1268(1⁄303-1⁄t)]} tiene en cuenta el ajuste necesario para calcular la conductividad a temperaturas superiores a 303 K [4]. Además, en el modelo presentado en este trabajo se definen dos coeficientes β y δ para poder aplicar la ecuación obtenida para el Nafion 117 a la modelación de celdas con otros materiales de membrana, los cuales tienen diferentes relaciones entre la conductividad, el contenido de agua y la temperatura. Por lo tanto, se emplea la ecuación (8).

En el modelo propuesto en este trabajo se asume pérdida de potencial en el cátodo y pérdidas óhmicas en la membrana. Para calcular la pérdida en el cátodo se tiene en cuenta la expresión de Tafel (ecuación 2) en la cual la corriente (I) es función de la pérdida de activación (η), que a su vez depende del voltaje de la celda (V_celda) ecuación (4), [2]. Como el voltaje de la celda se define como condición de contorno se puede calcular la corriente de la celda. Una simplificación importante del modelo presentado en este trabajo la constituye el hecho de no tener en cuenta el efecto que tiene un gran exceso de agua líquida en el cátodo. Este exceso puede causar una barrera para el transporte de los gases reaccionantes. Por lo tanto, el modelo es efectivo cuando las condiciones de funcionamiento están por debajo de los parámetros de formación de agua líquida en exceso en el cátodo. Esta cantidad de agua líquida puede aparecer a altas densidades de corriente, en las que la velocidad de la reacción es muy elevada.

Diseño de la celda de combustible PEM modelada

El diseño de la PEMFC que se modela es el de una celda plana porque presenta las ventajas de permitir un mejor acoplamiento de la pila en un menor volumen y posibilitar el diseño de placas bipolares que unen todas las celdas formando un único circuito eléctrico. La longitud de la celda estudiada es de 125 mm. En la figura 2, se muestran las dimensiones de la sección transversal definidas en el modelo.

Existen diferentes materiales que pueden ser empleados en el diseño de las PEMFC. En la tabla 1, se muestran los materiales correspondientes a la celda modelada.

En este modelo de celda PEM se establecen las condiciones de contorno al flujo de especies y de electrones. Con este objetivo se definen el flujo másico de gases a la entrada de los canales, la presión de los gases a la entrada del ánodo y del cátodo, la temperatura de los gases, el voltaje de operación de la celda y la presión de los flujos a la salida de los canales. Para analizar en el modelo la influencia que tiene en el rendimiento de la celda el material utilizado en la membrana, se definen las características de una membrana alternativa al Nafion. El electrolito escogido para este estudio fue la sulfonated-polyetheretherketone (SPEEK) de la empresa Vitrex por ser uno de los que mayores perspectivas muestra en cuanto a reducción de costo y flexibilidad del rango de operación de los parámetros termodinámicos[6]. En el modelo propuesto se definen las propiedades de este material, como se muestra en la tabla 2.

La conductividad iónica de la membrana SPEEK es inferior a la de la membrana Nafion. En el modelo esta propiedad se describe a partir de la ecuación (8). Teniendo en cuenta los resultados experimentales presentados en [5], se puede considerar que para la SPEEK el coeficiente β es 0,5. La ecuación (9), muestra la relación entre la conductividad y el contenido de agua y la temperatura para una membrana SPEEK.

Donde:
β: Conductividad eléctrica de la membrana SPEEK.

 

RESULTADOS Y DISCUSIÓN

La modelación de la PEMFC se realizó utilizando el software ANSYS FLUENT 14.5.

VALIDACIÓN DEL MODELO

Las curvas de polarización obtenidas por Songprakorp (2008) con su modelo están en los mismos rangos de valores analizados en este trabajo [8]. Los resultados que obtuvo este autor fueron comparados con los resultados experimentales de Bender según las curvas de polarización correspondientes [8]. La figura 3, muestra los resultados de la validación del modelo de la celda PEM presentado en este trabajo. Los resultados del modelo en FLUENT presentan buena coincidencia con los resultados de los otros dos autores para voltajes superiores a 0,62 V. Por debajo de este valor la diferencia entre los resultados aumenta, alcanzando la máxima incertidumbre a 0,44 V con un error de menos del 10 %. Esto puede estar debido a diferentes causas. La más importante es que dentro de las limitaciones del modelo propuesto, se explica que a altas densidades de corriente la exactitud de la solución obtenida pudiera afectarse por la presencia de agua líquida en exceso en el cátodo.

ANÁLISIS DE LOS PARÁMETROS DE OPERACIÓN

La variación de la presión y de la temperatura tiene una influencia directa en el rendimiento del dispositivo. La ecuación (10), conocida como ecuación de Nernst, describe el funcionamiento teórico de las PEMFC y establece que, en la medida que se aumenta la temperatura, el voltaje producido disminuye. Además, al aumentar la presión se incrementa el valor del voltaje.

Donde:
E: Potencial teórico producido en la celda y
P_H2 y P_O2: Presión del oxígeno y del hidrógeno respectivamente.

Los resultados de las modelaciones para diferentes valores de presión se muestran en la figura 4.

Se puede apreciar en la figura 4, que la potencia producida por la celda se incrementa al aumentar la presión de los gases. Berning (2003) y Ding (2014) también obtuvieron una mayor potencia para el máximo valor de presión analizado [9-10]. Estos resultados coinciden con el funcionamiento teórico de las celdas PEM.

Al aumentar la temperatura se afectan parámetros como la composición de los gases, la conductividad de la membrana y la densidad de corriente, sin embargo, el potencial teórico disminuye [9]. Los resultados obtenidos en la modelación se muestran en la figura 5.

Como se puede apreciar en la figura 5, se alcanza una mayor potencia a una temperatura de los gases de 343 K, para el rango analizado. Este comportamiento corresponde con el funcionamiento teórico de la celda descrito por la ecuación de Nernst. Songprakorp(2008),Díaz (2014) y Kokoh (2014) también obtuvieron rangos de voltaje en los que es preferente disminuir la temperatura y otros en los que es más favorable aumentarla [8-11-12]. Noorkami (2014) obtuvo las mayores potencias para los valores menores de temperatura analizados [13]. En el modelo inicial se consideró que los flujos de los gases circulan en sentido contrario. De esta forma las mayores concentraciones de oxígeno y de hidrógeno se encuentran en extremos opuestos de la celda. Cuando los flujos circulan en paralelo, la concentración de los reaccionantes disminuye en el mismo sentido, en la medida que son consumidos por la reacción. Los resultados de la modelación de la celda PEM con ambas alternativas se muestran en la figura 6.

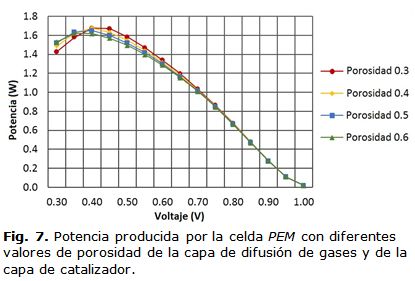
En la figura 6, se puede comprobar que el sentido en el que fluyen los gases a través de los canales no tiene gran influencia en el rendimiento de la PEMFC. A bajos voltajes de operación es que se establece la diferencia máxima en el funcionamiento del dispositivo. Para estos valores, la potencia producida por la celda con los flujos cruzados supera en poco más del 2 % a la potencia de la celda con los flujos paralelos. En el trabajo presentado por Sembler(2010) para las SOFC se obtiene igualmente la mayor potencia con los flujos de gases cruzados [14]. La variación de la porosidad tiene influencia en el rendimiento de la celda debido a la ocurrencia de dos fenómenos inversos. Uno de estos consiste en que las regiones porosas permiten la difusión de los gases reaccionantes, por lo tanto, un incremento en la porosidad significa que la difusión de especies aumenta. Sin embargo, en la medida que el medio es más poroso, la resistencia por contacto entre las interfaces de la celda se incrementa. Los resultados de la potencia generada por la celda teniendo en cuenta la variación de la porosidad se muestran en la figura 7.

Los resultados obtenidos muestran que la influencia de la porosidad en el rendimiento de la celda no es significativa. Existe un aumento de la potencia producida en el dispositivo cuando se reduce el valor de la porosidad, reduciéndose esta diferencia en la medida que aumenta el voltaje. La potencia que se genera para una porosidad de 0,3 supera en más del 1 % a la que se produce en el modelo inicial con porosidad de 0,5. Puede verificarse que para valores de voltaje mayores que 0,75 V la potencia se mantiene casi invariable al cambiar el valor de la porosidad. Esto se debe a que la variación de esta propiedad provoca dos efectos contrarios, como se explicó anteriormente, por lo que existen valores de voltaje en los que se complementan. Berning (2003) en su modelo obtuvo resultados en los que la potencia máxima también se alcanza para un valor de porosidad de 0,3. En este trabajo el autor analizó el efecto de este parámetro en un rango de 0,3 a 0,5 y la diferencia entre la potencia producida para cada valor es pequeña [9]. Para lograr la hidratación adecuada para el funcionamiento de la celda es necesario humidificar los gases a la entrada de los canales. En el modelo planteado se definió una humidificación inicial que constituye el 100 % de humedad relativa en el ánodo y el 75 % de humedad relativa en el cátodo. La figura 8, muestra la curva de potencia producida para diferentes niveles de humidificación inicial.

Estos resultados demuestran la influencia directa que tiene la humidificación de los gases en el contenido de agua de la membrana, y por lo tanto, en el rendimiento del dispositivo. La humidificación inicial permite alcanzar más del doble de la potencia que se logra sin humidificar los gases. En los trabajos presentados por Guvelioglu (2005) y Berning (2011) los resultados obtenidos también muestran que si se reduce la humidificación de los gases a la entrada de los canales, se reduce la potencia generada en el dispositivo [3-15].

OPTIMIZACIÓN DE LOS PARÁMETROS DE DISEÑO

Para lograr una correcta distribución de los gases es necesario que los canales de entrada de gases tengan las dimensiones adecuadas de ancho y alto. A mayor ancho de los canales, la difusión de los gases ocurrirá a través de una mayor superficie de la capa difusora. Sin embargo, el paso de los electrones entre los electrodos y los colectores. Se analizaron seis modelos con dimensiones del perfil diferentes para obtener la relación óptima de ancho y alto, manteniendo el perímetro del perfil constante. Los resultados obtenidos se muestran en la figura 9.

Los resultados obtenidos muestran que a voltajes inferiores a 0,45 V se favorecen los diseños de mayor ancho, mientras que en el resto de los valores se favorecen los diseños de menor ancho. Analizando la potencia total generada para todos los valores de voltaje, se verifica que la configuración que mayor potencia genera es la que posee 0,5 mm de ancho y 0,9 mm de alto. Este resultado muestra que, en los rangos de valores estudiados, el movimiento de los electrones tiene preferencia sobre la difusión de los gases. Según Guvelioglu (2005), para densidades de potencia elevadas es más favorable que la dimensión del ancho sea lo más reducida posible [3]. La longitud de los canales es uno de los factores que determina el consumo de combustible en la celda. Por lo tanto, se debe encontrar cuál es la longitud para la cual se obtiene el mayor rendimiento del dispositivo. En la figura 10, se muestra la curva de potencia generada en la celda PEM con una longitud de los canales de 100 mm, 125 mm y 150 mm, donde 125 mm es el valor inicial.

Como se puede verificar en la figura 10, la longitud del canal tiene poca influencia en la densidad de potencia producida en la celda. Con una longitud de 150 mm de largo se alcanza una potencia que supera en más del 1% a la potencia del modelo con 125 mm y en más del 2 % a la del modelo con 100 mm. Esto se debe a que para las longitudes más pequeñas de los canales, la cantidad de hidrógeno que participa en la reacción electroquímica es insuficiente para lograr un rendimiento óptimo. La figura 11, muestra los contornos de utilización del combustible teniendo en cuenta un factor de escala de 0,1 en el eje "z".

En los contornos de utilización del combustible de cada dispositivo se puede verificar que en la celda de menor longitud la concentración de hidrógeno a la salida del canal del ánodo es muy elevada. La celda en la que existe una mayor disminución de la concentración del combustible es la que posee 150 mm de longitud. Teniendo en cuenta las propiedades del material definidas en FLUENT, principalmente la conductividad iónica, se calculó la potencia que genera la celda con una membrana SPEEK, como se muestra en la figura 12.

La celda con electrolito de Nafion produce una potencia superior a la celda con membrana SPEEK. Este es un resultado esperado porque el Nafion permite el paso de una mayor cantidad de iones. Sin embargo, la membrana SPEEK tiene un precio más bajo y permite que el dispositivo funcione a temperaturas superiores a los 373 K sin afectar el rendimiento. Actualmente muchas investigaciones se dirigen a mejorar la conductividad iónica de este material y a encontrar otros materiales alternativos.

 

CONCLUSIONES

Se desarrolló un modelo tridimensional en CFD de una celda PEM en la cual se analizó el rendimiento del dispositivo y se obtuvieron las siguientes conclusiones:

• La variación de los parámetros termodinámicos presión y temperatura causa el efecto sobre el rendimiento de la PEMFC descrito por la ecuación de Nernst. La potencia que se produce aumenta al incrementar el valor de la presión en un rango de 101325 Pa a 150000 Pa. Este efecto también ocurre cuando se disminuye la temperatura en el rango de 343 K a 363 K.

• La variación de la porosidad de la capa de difusión de gases y del sentido de los flujos de gases a través de los canales provoca una modificación mínima en el rendimiento del dispositivo. La potencia que genera la celda con un valor de porosidad de 0,3 supera en poco más del 1 % a la que genera el modelo inicial con una porosidad de 0,5. Con los flujos de gases cruzados se produce un rendimiento que supera en 1% al que se alcanza con los flujos de gases paralelos.

• El rendimiento de la celda PEM presenta gran sensibilidad a la variación de la humidificación de los gases. Cuando los gases a la entrada de los canales están secos, la potencia que se genera es menos del 50 % de la potencia producida por el dispositivo con un 75 % y un 100 % de humedad relativa en el cátodo y en el ánodo respectivamente.

• En la optimización del perfil de los canales para la celda PEM modelada, la cual genera alta densidad de corriente, el rendimiento de la celda aumenta con el área de transferencia de los electrones, más que con el aumento del área de difusión de gases. El perfil óptimo obtenido posee 0,5 mm de ancho y 0,9 mm de alto, y genera una potencia que supera en más del 3 % a la que genera el modelo inicial con 0,8 mm de ancho y 0,6 mm de alto.

• Para realizar la modelación de una PEMFC con un electrolito diferente al Nafion, fue necesario modificar la ecuación que caracteriza la conductividad iónica. Por lo tanto, se consideró el comportamiento experimental de esta propiedad en el nuevo material para diferentes valores del contenido de agua y la temperatura.

 

AGRADECIMIENTOS

Los autores desean agradecer a las entidades que han hecho posible la realización de este artículo, en el marco del proyecto de cooperación CAPES-MES, entre el Ministerio de Educación de Brasil y el Ministerio de Educación Superior de Cuba. CAPES es una agencia gubernamental brasileña que se dedica al desarrollo de capital humano.

 

REFERENCIAS

1. GUPTA, R.B., Hydrogen Fuel: Production, Transport and Storage.CRC Press, 2009, [consultado: 25 de mayo de 2013], Disponible en: www.crcpress.com/product/ISBN:/9781420045758, ISBN: 978-1-4200-4577-2.

2. ALHAZMI, N.; et al., "Effect of the anisotropic thermal conductivity of GDL on the performance of PEM fuel cells". International Journal of Hydrogen Energy, 2013, vol.38, n.1, p. 603-611, ISSN 0360-3199.

3. GUVELIOGLU, G.H.; STENGER, H.G., "Computational fluid dynamics modeling of polymer electrolyte membrane fuel cells". Journal of Power Sources, 2005, vol.147, n.1-2, p. 95-106, ISSN 0378-7753.

4. KO, J.; JU, H., "Effects of cathode catalyst layer design parameters on cold start behavior of polymer electrolyte fuel cells (PEFCs)". International Journal of Hydrogen Energy, 2013, vol.38, n.1, p. 682-691, ISSN 0360-3199.

5. WILKINSON, D.P.; et al., Proton Exchange Membrane Fuel Cells: Materials Properties and Performance. CRC Press, 2010, [consultado: 25 de mayo de 2013], Disponible en: www.technology.matthey.com/pdf/225-228-pmr-oct11.pdf, ISBN: 1439806667.

6. MARANGIO, F.; et al., "Concept of a high pressure PEM electrolyser prototype". International Journal of Hydrogen Energy, 2011, vol.36, n.13, p. 7807-7815, ISSN 0360-3199.

7. WU, H.L.; et al., "Sulfonated poly (ether ether ketone)/poly(amide imide) polymer blends for proton conducting membrane". Journal of Membrane Science, 2006, vol.280, n.1-2, p. 501-508, ISSN 0376-7388.

8. SONGPRAKORP, R., "Investigation of Transient Phenomena of Proton Exchange Membrane Fuel Cells". Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor in Philosophy in the Department of Mechanical Engineering, Canada: University of Victoria, 2008, [consultado: 25 de mayo de 2013], Disponible en: http://www.iesvic.uvic.ca/pdfs/Dissertation-Songprakorp.pdf, ISBN: 0494473401.

9. BERNING, T.; DJILALI, N., "Three-dimensional computational analysis of transport phenomena in a PEM fuel cell-a parametric study". Journal of Power Sources, 2003, vol.124, n.2, p. 440-452, ISSN 0378-7753.

10. DING, Y.; et al., "Numerical investigation of the impact of two-phase flow mal distribution on PEM fuel cell performance". International Journal of Hydrogen Energy, 2014, vol.39, n.1, p. 469-480, ISSN 0360-3199.

11. DÍAZ, M.; et al., "Performance of PEMFC with new polyvinyl-ionic liquids based membranes as electrolytes". International Journal of Hydrogen Energy, 2014, vol.39, n.8, p. 3970-3977, ISSN 0360-3199.

12. KOKOH, K.B.; et al., "Efficient multi-metallic anode catalysts in a PEM water electrolyzer". International Journal of Hydrogen Energy, 2014, vol.39, n.5, p. 1924-1931, ISSN 0360-3199.

13. NOORKAMI, M.; et al., "Effect of temperature uncertainty on polymer electrolyte fuel cell performance". International Journal of Hydrogen Energy, 2014, vol.39, n.3, p. 1439-1448, ISSN 0360-3199.

14. SEMBLER, W.J.; KUMAR, S., "Optimization of a Single-Cell Solid-Oxide Fuel Cell Using Computational Fluid Dynamics". En: ASME 2010 8^th International Conference on Fuel Cell Science, Engineering and Technology.New York, USA, June 14-16, 2010, p. 1-14, [consultado: 10 de mayo de 2013], Disponible en: http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleID=1610553, ISBN: 978-0-7918-3875-4.

15. BERNING, T.; et al., "Water balance simulations of a polymer-electrolyte membrane fuel cell using a two-fluid model". Journal of Power Sources, 2011, vol.196, n.15, p. 6305-6317, ISSN 0378-7753.

 

 

Recibido: marzo de 2014
Aprobado: agosto de 2014

 

 

Raciel de la Torre Valdés. Ingeniero en Tecnologías Nucleares y Energéticas, Profesor del Departamento de Ingeniería Nuclear, Facultad de Ciencias y Tecnologías Nucleares, Instituto Superior de Tecnologías y Ciencias Aplicadas, InSTEC, La Habana, Cuba. email: [e-mail]; [e-mail]