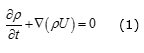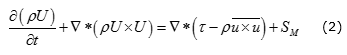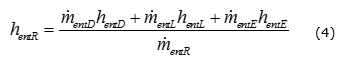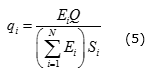APLICACIONES INDUSTRIALES

 

Metodología para el cálculo acoplado neutrónico-termohidráulico del reactor nuclear de agua ligera de alto desempeño

Coupled Neutronics/ Thermal-hydraulics Analysis Methodology of a High Performance Light Water Reactor

 

 

M.Sc. Landy Castro González¹; MSc. Carlos García Hernández¹; Dr. C. T. Leorlen Rojas Mazaira¹; Dr. C. T. Carlos Brayner de Olivera Lira²

Instituto Superior de Tecnologías y Ciencias Aplicadas. Facultad de Ciencias y Tecnologías Nucleares. Cuba.
Universidad Federal de Pernambuco. Departamento de Ingeniería Nuclear. Brasil.

---

RESUMEN

El uso del agua supercrítica como refrigerante en los reactores nucleares es un reto para su diseño y operación, pues es necesario tener en cuenta la fuerte influencia de las propiedades termodinámicas del agua supercrítica enlas propiedades moderadoras de los neutrones. En este trabajo se desarrolló una metodología basada en un código de Monte-Carlo para el cálculo neutrónico y un código de dinámica de fluido computacional para el cálculo termohidráulico, con el objetivo de realizar el cálculo acoplado neutrónico-termohidráulico de un conjunto combustible de un reactor de agua supercrítica de alto desempeño. Empleando la metodología desarrollada fueron obtenidos los perfiles de temperatura y potencia liberada en las barras combustibles del conjunto, los de temperatura en la envoltura de los elementos combustibles y los perfiles de temperatura y densidad del agua en la zona refrigerante y en la zona moderadora del conjunto. Los resultados describen acertadamente el comportamiento de dichos parámetros en el conjunto combustible promedio.

Palabras clave: agua supercrítica, dinámica de fluidos computacional, cálculo termo-hidráulico, reactores nucleares.

---

ABSTRACT

The use of supercritical water as a coolant in nuclear reactors is a challenge for its design and operation, it is necessary to consider the strong dependence between the thermodynamic properties of supercritical water and the properties as moderator of neutrons. This paper presents a methodology based on a Monte-Carlo code for neutronic calculation and a computational fluid dynamics code for thermohydraulic calculation, with the aim of making the coupled neutronic-thermohydraulic analysis of a High Performance Light Water Reactorfuel assembly. Using the developed methodology, temperature profiles and power released in the fuel rods, the cladstemperature distribution and the temperature and water density profiles in the cooling and moderator zone were obtained. The results, accurately, describe the behavior of these parameters in the average fuel assembly.

Key Words: supercritical water, computational fluids dynamics, coupled analysis, nuclear reactors.

---

 

 

INTRODUCCIÓN

La energía nuclear ha probado tener gran capacidad para la producción de energía eléctrica y además sin emisiones de CO₂ durante el proceso productivo. En términos de sostenibilidad, cambio climático, calidad del aire y energía segura, juega un papel importante en la energética del futuro.

Sin embargo, para mejorar su desempeño debe vencer los siguientes retos.

• Bajar los costos de construcción y operación.
• Mejorar la eficiencia energética.
• Disminuir los riesgos de proliferación nuclear, debido a que los isótopos de plutonio que se generan durante el proceso (especialmente el Pu239) pueden ser utilizados en la fabricación de armas nucleares.
• Manejo de los residuos radiactivos delarga vida, especialmente los llamados elementos transuránicos.

En el Foro Internacional de Reactores Nucleares de Generación IV, se propusieron 6 tipos de reactores nucleares para satisfacer los objetivos mencionados [1]. Estos son: reactor refrigerado por agua supercrítica (SCWR, por sus siglas en ingles), reactor rápido refrigerado por gas, reactor rápido refrigerado por sodio, reactor rápido refrigerado por plomo, reactor de muy alta temperatura y el reactor refrigerado por sales fundidas. Entre ellos el SCWR es uno de los más viables [2], principalmente por la mejora introducida en la eficiencia energética, por lo que debe generar electricidad con menor costo. En este reactor se incrementaría la eficiencia del ciclo termodinámico desde un 33 %, característica de los convencionales reactores de agua ligera (LWR, por sus siglas en inglés), a un 45 %.

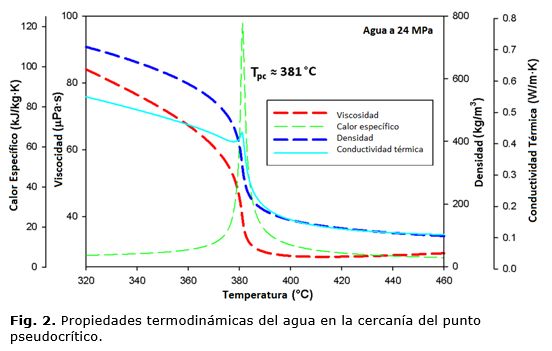
El conocimiento de las principales propiedades termofísicas del agua supercrítica resulta de vital importancia para entender los fenómenos que ocurren dentro del núcleo de un SCWR. El agua al alcanzar los valores conocidos como punto crítico, presión de 22,1 MPa y una temperatura de 374, pierde la distinción entre las fases líquida y gaseosa, ver figura 1. Por encima de esta temperatura y presión, se dice que el agua es supercrítica y se comporta de manera muy diferente al agua subcrítica. La diferencia más significativa que existe entre las propiedades del agua sub y supercrítica es el valor de calor específico y particularmente su comportamiento en el punto crítico. La densidad, la viscosidad y la conductividad térmica como se aprecia en la figura 2, disminuyen apreciablemente con la temperatura. Como consecuencia del alto valor de calor específico puede ocurrir una mayor transferencia de calor, permitiendo reducir el flujo másico en el circuito de enfriamiento.

Desde 1950 se introdujo la idea de usar agua supercrítica (SCW, por sus siglas en ingles) en los generadores de vapor de las centrales nucleares, como no existe cambio de fase, el flujo de calor crítico no ocurre, el cual es uno de los principales parámetros de seguridad y limitante para la operación del reactor[3].

Hoy en día el uso del SCW ha alcanzado una considerable penetración en el mercado de la producción de energía eléctrica [4]. Su aplicación en sistemas de generación de energía convencionales, como las termoeléctricas de carbón ha sido comprobada con éxito a lo largo de los años. En general, la eficiencia del ciclo termodinámico de las termoeléctricas modernas que trabajan a parámetros subcríticos es de alrededor de 36-38 %, pero es posible alcanzar 45-50 % al trabajar a parámetros supercríticos. El conocimiento acumulado en el uso del SCW en la industria convencional es de gran relevancia y está siendo empleado para el diseño de los SCWR. Estos reactores ofrecen muchas ventajas comparados con los reactores convencionales actuales, además del aumento de la eficiencia térmica, poseen un circuito de flujo simplificado de ciclo directo de un solo paso, que es el tipo más simple posible [5], donde el agua entra al reactor como líquido subcrítico y sale a altos valores de temperatura y presión, por encima del punto crítico. No ocurre cambio de fase, por lo que el agua supercrítica es introducida directamente a la turbina de alta presión, sin necesidad de intercambiadores de calor intermedios. Este tipo de ciclo posee una ventaja económica significativa, pues simplifica apreciablemente el diseño de la planta, eliminando los típicos intercambiadores de calor y presurizadores de los Reactores de Agua a Presión (PWR, por sus siglas en ingles), y no necesitan separadores de vapor, ni secadores, ni bombas de recirculación típicas de los Reactores de Agua Hirviente (BWR, por sus siglas en ingles). La vasija del reactor y las barras de control son similares al PWR, la contención y los sistemas de seguridad son comparables al BWR y el balance termodinámico es comparable a una termoeléctrica de carbón supercrítica [5]. Las ventajas de los SCWR en relación con los LWR convencionales están expuestas de forma resumida por Oka (2002) [6]. Debido a todas las mejoras económicas potenciales que presenta este tipo de tecnología, reportadas por Oka (1993) [7], el concepto del SCWR resulta muy atrayente para la producción de energía,por los bajos costos de producción y la seguridad de su diseño basada en la combinación de dos tecnologías de eficacia comprobada, los reactores convencionales y las calderas supercríticas de carbón convencionales [8].

La utilización de agua supercrítica como refrigerante, hace que su densidad varíe fuertemente con la temperatura a través del núcleo del reactor, especialmente en la zona baja y central donde ocurre la transición de agua suscritica a supercrítica, conocida como línea pseudocrítica. La densidad del agua dentro del núcleo del reactor está relacionada directamente con propiedades neutrónicas como la moderación y la absorción de neutrones. Lo anteriorinfluye en la distribución de potencia y esta a su vez determina los perfiles de densidad del agua dentro del reactor. Debido a la fuerte interacción entre la distribución axial de potencia y de densidad del agua, resulta imprescindible realizar los cálculos de forma acoplada, entre el cálculo neutrónico y el termohidráulico.

Se han realizado numerosos estudios acoplados como el realizado por Waata (2006) [2], donde se analiza el comportamiento termohidráulico del diseño europeo del reactor supercrítico denominado reactor de agua ligera de alto desempeño(HPLWR, por sus siglas en inglés). Otros estudios se han realizado considerando la densidad del refrigerante y el moderador constante dentro del núcleo, arrojando resultados notablemente diferentes. En la actualidad los estudios de seguridad y diseño de los SCWR adoptan el método acoplado. Oka (2010) ha realizado numerosos estudios de diseño y cálculos de seguridad de los HPLWR utilizando esta metodología[9]. Shan (2009) estudió el SCWR de tipo tubo de presión utilizando esta metodología [10]. Khurrum (2013) desarrolló un sistema para el cálculo acoplado de un HPLWR usando MCNP4C y un código termohidráulico SACOS, donde comparóla distribución de potencia lineal, realizando el cálculo desacoplado, parcialmente acoplado sin considerar el efecto de retroalimentación y totalmente acoplado. En los resultados mostraron una notable diferenciaen la distribución de potencia axial [11].

En este trabajo se desarrolla una metodología para el cálculo acoplado neutrónico termo-hidráulico de un HPLWR, se usa para los cálculos neutrónicos el código MCNPX2.6e [12], y para el cálculo termo hidráulico el código de Dinámica de Fluidos Computacional (CFD), CFX-14. Usando la metodología desarrollada se determinan los perfiles de temperatura y potencia liberada en las barras combustibles del conjunto, los perfiles de temperatura en la envoltura de los elementos combustibles y los perfiles de temperatura y densidad del agua en la zona refrigerante y en la zona

MATERIALES Y MÉTODOS

Características del HPLWR

Existen varios diseños de conjuntos combustibles para los HPLWR [13]. Algunos de geometría cuadrada y otros de geometría hexagonal. En cada diseño la presión de operación y las temperaturas de entrada y salida del núcleo del reactor del fluido refrigerante son de alrededor de 25 MPa, 280 y 5000C, respectivamente. La densidad del refrigerante disminuye desde aproximadamente 760kg/m³ en la entrada del núcleo a aproximadamente 90 kg/m³ en la salida.

En el caso de los SCWR es común que además del agua que hace la función de refrigerante exista en el conjunto combustible una cantidad de agua con la función de moderador. En el HPLWR el flujo de agua moderadora desciende por la parte central interior del conjunto combustible, denominada moderador interior y también por el espacio entre las cajas que encierran los elementos combustibles, denominado moderador exterior.

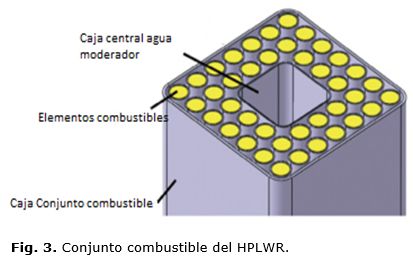
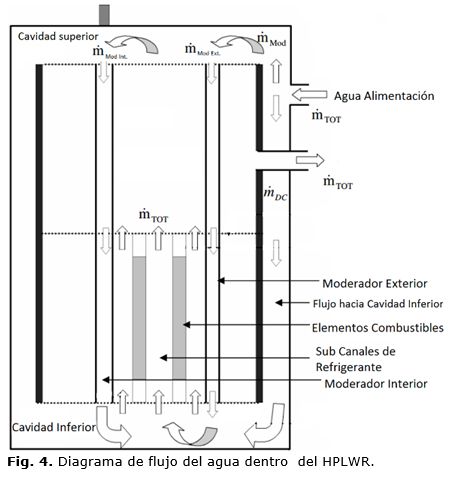
Hofmeister (2007), demuestra que el conjunto combustible cuadrado con dos filas de barras combustibles en un arreglo de 7x7 elementos alrededor de una caja central de agua moderadora de neutrones, ver figura 3, resulta ser el diseño óptimo para el conjunto combustible del HPLWR. Este diseño tiene pequeña proporción de material estructural-combustible para minimizar la absorción de neutrones y la relación moderador-combustible está mucho más cerca a la de un PWR que otros diseños [14]. En la figura 4, se muestra el diagrama de flujo de agua dentro del reactor. El agua al entrar al reactor se divide en dos flujos uno ascendente hasta la cavidad superior para posteriormente descender como moderador interior y exterior. El otro flujo desciende hasta la cavidad inferior, donde se mezcla con el agua moderadora y asciende por entre los elementos combustibles como refrigerante.La densidad del agua refrigerante disminuye con el incremento de la altura del conjunto a diferencia del agua moderadora que aumenta su densidad con la altura.

 

Metodología para el cálculo neutrónico-termohidráulico acoplado

Para el cálculo termohidráulico de reactores nucleares usualmente se utilizan códigos tradicionales que emplean modelos simples como el RELAP, ATHLET, CATHARE, COBRA, MATRA, etc. Estos códigos utilizan relaciones semiempíricas basadas en datos experimentales, generalmente limitados para pequeños rangos de temperatura, presión y para configuraciones geométricas específicas [2]. La mayoría de estos datos experimentales han sido obtenidos para geometrías simples, sin tener en cuenta las particularidades del comportamiento del agua supercrítica en geometrías complejas similares a los subcanales de los conjuntos combustibles de un HPLWR. Ello debido, principalmente, al elevado costo de las instalaciones experimentales.

Recientemente el uso de las técnicas de CFD ha sido una alternativa fiable para predecir el comportamiento termohidráulico en reactores nucleares supercríticos. Una característica distintiva de las simulaciones en CFD es el enfoque que realiza para la descripción de procesos físicos. En lugar de utilizar las propiedades promediadas del fluido, este utiliza una distribución espacial de las mismas permitiendo captar fenómenos locales, de vital importancia para el diseño y la seguridad de los reactores nucleares.

Los códigos que utilizan CFD tienen en cuenta la variación espacial de las propiedades de los fluidos y resuelven numéricamente las ecuaciones (1), (2) y (3), para llegar a una simulación completa del comportamiento del sistema.

Continuidad:

Momento:

Energía:

donde: ρ es la densidad del agua, U es la velocidad, λ es la conductividad térmica, ∇(U · t) es un término que representa el trabajo realizado por las fuerzas viscosas, h_tot es la entalpía total, S_MySE son los términos fuente relacionados a las fuerzas de cuerpo, y t el tensor de cizallamiento. La mayor dificultad para la modelación termohidráulica del SCW utilizando CFD está relacionada con los modelos de turbulencia a presiones supercríticas, pues resulta complejo predecir la transferencia de calor y obtener las distribuciones de las distintas propiedades termodinámicas del agua supercrítica, debido a las grandes variaciones de las propiedades termofísicas en la cercanía de la línea pseudocrítica. En estas condiciones la aplicabilidad de los modelos convencionales de turbulencia no está suficientemente verificada. En estudios anteriores se demostró la efectividad del empleo del modelo k - e para predecir la turbulencia del agua supercrítica en los subcanales del conjunto combustible del HPLWR [15]. En este estudio se emplea el modelo de turbulencia k - e. Este modelo de turbulencia es el más conocido de los modelos de dos ecuaciones para el transporte de energía. La variable k representa la energía cinética total de la turbulencia y e representa la tasa de disipación de dicha energía.

La selección del código MCNPX2.6e para la realización del cálculo acoplado neutrónico termo hidráulico ofrece grandes ventajas, pues permite la modelación detallada de geometrías complejas en 3D, y permite considerar la heterogeneidad del núcleo del SCWR.

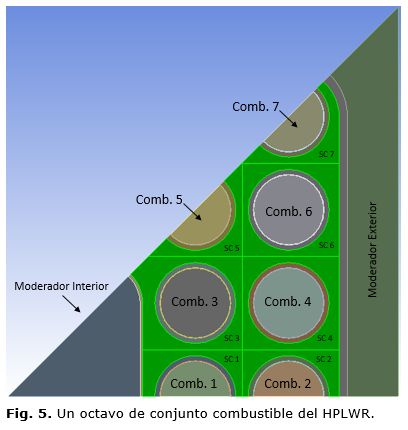
Generación de la geometría

Debido a la notable simetría del conjunto combustible, se consideró un octavo del mismo como se muestra en la figura 5, donde se identifican los subcanales de refrigerante y los elementos combustibles, compuestos por el combustible nuclear y una envoltura de acero que contiene dicho combustible y los productos de fisión generados. El combustible nuclear es  enriquecido al 5 % en peso en U235, para todos los elementos combustibles, a excepción de las esquinas, que se enriquece al 4 % para contrarrestar el exceso en la  moderación de neutrones que ocurre en esa zona. Las dimensiones del conjunto combustible se muestran en la tabla 1.

Discretización espacial

La forma de la malla y la cantidad de elementos utilizados para discretizar el espacio depende de la geometría, y la exactitud requerida de la solución. En el presente estudio se utilizó una malla estructurada para adaptarse a la geometría del canal. En las cercanías de las paredes se realiza un refinamiento de la malla para garantizar que los gradientes de velocidad y temperatura se resuelvan correctamente, y además cumplir con todos los requisitos del modelo de turbulencia con tratamiento especial cercano a las paredes, que desempeña un papel significativo en la precisión del cálculo de los esfuerzos cortantes y el coeficiente de transferencia de calor. Para obtener resultados exactos con el modelo de turbulencia seleccionado se garantiza que la distancia adimensional a la pared y+, se encuentre siempre en un valor inferior a 1.

 A fin de verificar la independencia de la solución del paso de la red, se realiza un estudio de diversas configuraciones de la malla, en un clúster de computadoras con 24 procesadores de última generación con una capacidad de memoria de 120 GB, que permite realizar estudios avanzados con elevada precisión. Se obtuvo que con una malla de 48 032 500 elementos se alcanza una solución independiente del tamaño de la misma. En la figura 6, se muestra la sección transversal del subcanal y la amplificación local en la zona de la pared de las envolturas de los elementos combustibles. La malla se genera utilizando el método de multizona, con elementos tipo hexaedros y prismáticos.

Condiciones de fronteras

Las condiciones de fronteras incluyen la temperatura de entrada del moderador, flujo másico de refrigerante y moderador, la potencia generada a partir del flujo neutrónico calculado, etc. En la tabla 2, se muestran las condiciones de fronteras para el cálculo termohidráulico.

Para obtener la entalpía de entrada de la mezcla de agua que actúa como refrigerante se utiliza la ecuación (4).

Después de haber definido todas las condiciones para el cálculo acoplado se procede a inicializar el cálculo según el diagrama que se muestra en la figura 7.

Primeramente, se calcula la distribución de potencia axial en los elementos combustibles con el código MCNPXv2.6 asumiendo un perfil de densidad del refrigerante y moderador constante con un valor de densidad de 700 kg/m³ y de temperatura de 553 K.

Los datos recogidos de las interacciones de los neutrones son representativos de la población de neutrones y la energía depositada estimada, que se corresponde con la distribución de potencia. El recuento de energía está representado en MCNP por la tarjeta de recuento F7, con esta tarjeta se obtiene la energía de fisión promedio para cada sección del conjunto. El flujo de calor generado por cada elemento combustible se calcula mediante la ecuación (5).

siendo E_i la energía de fisión, S_i es la superficie del elemento combustible y Q es la potencia total del elemento combustible. La distribución de potencia obtenida se introduce en el ANSYS-CFX como condición de frontera en las paredes internas de las envolturas de los elementos combustibles. Como resultado de la modelación se obtiene la distribución de temperatura y de la densidad del agua supercrítica. Los datos actualizados de los materiales se introducen nuevamente en el MCNPX para una nueva estimación del perfil axial de potencia. La distribución de potencia de cada elemento combustible se calcula mediante la ecuación (5), y se compara con la anterior, realizando un proceso iterativo que converge cuando el error relativo de los resultados entre las iteraciones sea menor que el 1 %. Debido a la disminución de la densidad del agua refrigerante y el aumento de la densidad del agua moderadora desde la parte inferior a la superior de la zona activa, se espera que ocurra una oscilación de la posición del valor máximo de potencia lineal, en el proceso iterativo, cambiando desde la posición inferior en la primera iteración a la zona superior del canal en la iteración siguiente (2), [2]. Para evitar estas oscilaciones en el proceso iterativo se introduce una técnica numérica para acelerar la convergencia del cálculo acoplado. Se aplica un método de relajación a los valores de potencia obtenidos del cálculo neutrónico con un factor de relajación de 0,5, según la ecuación (6).

Para demostrar la convergencia del cálculo acoplado se muestra la figura 8. Se realizó el cálculo siguiendo el esquema de la figura 7, alcanzando la convergencia en la iteración 7. Los resultados del cálculo de las 7 iteraciones se muestran para la distribución axial de flujo de calor promedio de las barras de combustible. La historia del proceso iterativo muestra un máximo en el perfil axial de potencia en la zona inferior del núcleo y en la zona superior una tendencia inicial a un valor constante que comienza a visualizarse en la iteración 2, pero que posteriormente se hace menos acentuado hasta alcanzar la convergencia con un comportamiento decreciente.

RESULTADOS Y DISCUSIÓN

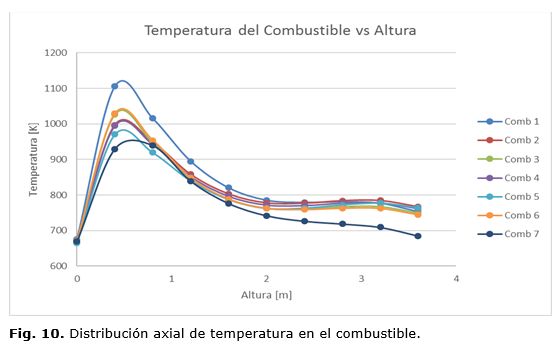
Usando esta metodología,basada en CFD, para el cálculo acoplado neutrónico-termohidráulico,se calcularon para el estado estacionario de operación los perfiles de temperatura y potencia liberada en las barras combustibles del conjuntocombustible de un HPLWR, además de los perfiles de temperatura en la envoltura de los elementos combustibles y los perfiles de temperatura y densidad del agua en la zona refrigerante y en la zona moderadora del conjunto. En la figura 9, se muestra la distribución axial de la potencia lineal para los elementos combustibles del octavo del conjunto combustible analizado. Los perfiles muestran un máximo de potencia lineal a aproximadamente 0,8 m de altura del canal. En los canales 5 y 7 se obtienen los valores menores de potencia lineal debido a que el canal 5 se ubica en el punto más alejado de la caja de agua moderadora y el elemento combustible 7 posee un menor enriquecimiento de combustible fisil. La figura 10, muestra la distribución de temperatura axial de las zonas de combustible nuclear para cada elemento. Se puede apreciar que el elemento combustible más cargado es el 1 cuyo valor máximo de temperatura se alcanza en la zona baja del núcleo y no excede los 1 200 K que es muy inferior a la temperatura de fusión del combustible de 3 000 K. Garantizándose un amplio margen de seguridad para la operación de dicho reactor.

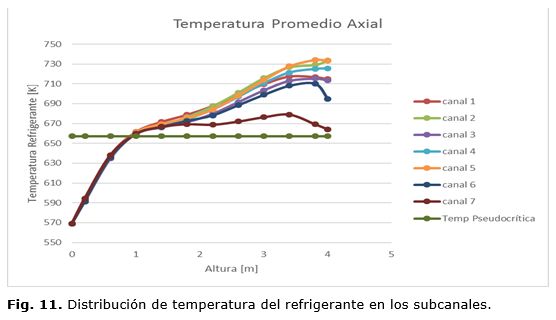
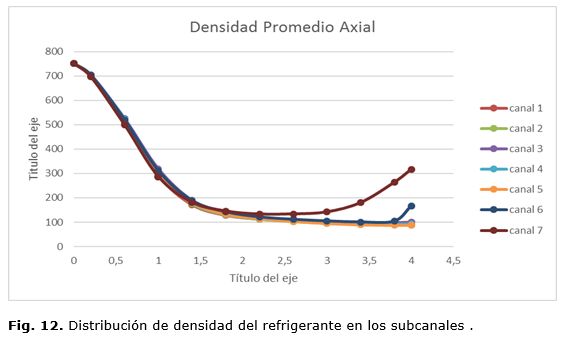
El perfil de temperatura axial del refrigerante se muestra en la figura 11, para cada subcanal. La temperatura pseudocrítica se alcanza aproximadamente a 1 m de altura del núcleo del reactor, los subcanales centrales alcanzan mayores valores de temperatura, y el subcanal 7 alcanza menor temperatura debido al intercambio térmico entre este canal y el agua que desciende como moderadora exterior. La figura 12, muestra la distribución de densidad del refrigerante en cada subcanal. Se obtiene una distribución de densidad uniforme para la mayoría de los subcanales a excepción de los subcanales 6 y 7, donde la densidad es mayor debido al intercambio térmico que existe entre este canal y el agua que desciende como moderadora exterior. La densidad promedio del refrigerante dentro del conjunto combustible desciende desde 750 kg/m³ a la entrada hasta 136 kg/m³ a la salida del núcleo del reactor.

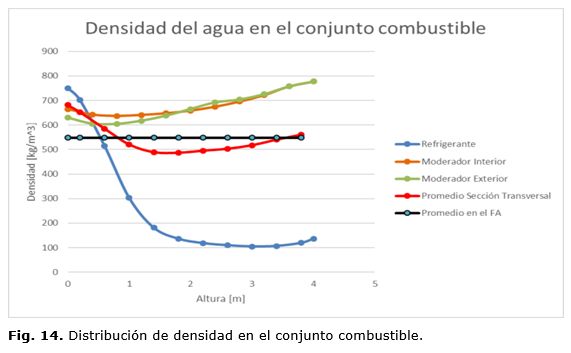
 En la figura 13, se dan las distribuciones axiales de temperaturaen la superficie de la envoltura de los elementos combustibles analizados. Existe correspondencia entre las distribuciones axiales de temperatura en la envoltura y las distribuciones axiales de potencia lineal en los elementos combustibles. En la figura 14, se muestran las distribuciones axiales de la densidad del agua en los subcanales, en el moderador interno, en el externo, en la sección transversal total del conjunto combustible (valor promedio de las tres zonas). La densidad del agua en ambas zonas moderadoras decrece según el sentido del flujo descendiente desde 770 kg/m³ hasta 664 y 629 kg/m³ respectivamente. La densidad del agua en la sección transversal del conjunto combustible es mayor en la entrada del núcleo, con un valor de 681 kg/m³, decrece hasta 486 kg/m3 a la altura de 1,5 m y comienza a aumentar hasta alcanzar un valor de 560 kg/m³ debido a la influencia del alto valor de densidad del agua moderadora en la zona superior del núcleo del reactor.

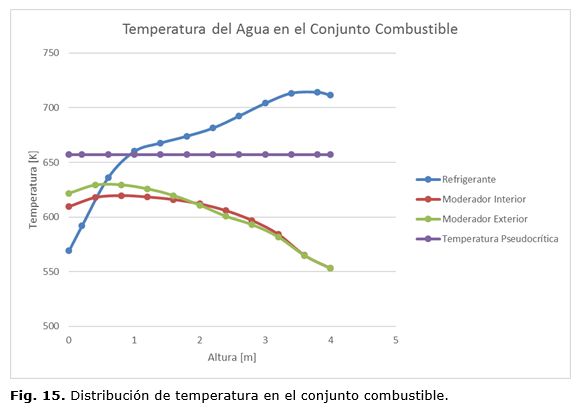
Las distribuciones axiales de temperatura del agua refrigerante y del agua moderadora se representan en la figura 15. La temperatura del moderador no alcanza la temperatura pseudocrítica. Debido a la transferencia de calor entre el refrigerante y el moderador la temperatura del moderador aumenta en el sentido del flujo descendente desde 553 K hasta 609-621 K.

 

CONCLUSIONES

El uso de agua super crítica es muy ventajoso para la refrigeración del núcleo de reactores nucleares y por ende el SCWR es uno de los candidatos de mayores perspectivas para la nueva generación de centrales nucleares. En el trabajo se presentó una metodología para el cálculo acoplado neutrónico-termohidráulico del conjunto combustible de un reactor de agua supercrítica de alto desempeño, basada en el código de Monte-Carlo MCNPXv2.6 para el cálculo neutrónico y el código de CFD CFX-14 para el cálculo termohidráulico. Con las herramientas desarrolladas se analizó el comportamiento de un conjunto de parámetros que caracterizan el estado estacionario de operación del conjunto combustible del reactor HPLWR. Los perfiles axiales obtenidos de potencia lineal, de temperatura del combustible, temperatura del agua refrigerante y el agua moderadora, y de densidad del refrigerante describen acertadamente el comportamiento de dichos parámetros en el conjunto combustible promedio del reactor HPLWR. La metodología desarrollada permite realizar futuros estudios de estados de operación y transitorios relacionados con la seguridad de dichas instalaciones.

 

REFERENCIAS

1. Ruzickova M. Overview and Progress in the European Project: Supercritical Water Reactor e Fuel Quali fi Cation Test. Progress in Nuclear Energy. 2014;77:381-389. ISSN 0149-1970. DOI 10.1016/j.pnucene.2014.01.011.

2. Waata CL. Coupled neutronics thermal hydraulics analysis of a high-performance light-water reactor fuel assembly. [doctoral Thesis]. Karlsruhe GmbH: Forschungszentrum 2006. [Citado marzo de 2015]. Disponible en: http://elib.uni-stuttgart.de/opus/volltexte/2006/2751/pdf/FZKA7233_Waata.pdf.

3. Farah A. Assessment of FLUENT CFD Code as an Analysis Tool for SCW Applications [Master of Applied Science in Nuclear Engineering]. Canada: University of Ontario Institute of Technology; 2012. [Citado marzo de 2015]. Disponible en: https://ir.library.dc-uoit.ca/xmlui/bitstream/handle/10155/239/Farah_Amjad.pdf

4. Baindur S. Materials challenges for the supercritical water cooled reactor (SCWR). Bulletin of the Canadian Nuclear Society. 2008;29:32-38.

5. Gu HY, Cheng X, Yang YH. CFD analysis of thermal-hydraulic behavior of supercritical water in sub-channels. Nuclear Engineering and Design. 2010;240(2):364-374. DOI 101016/jnucengdes200808022.

6. Oka Y, et al. Elements of Design consideration of Once-Through Cycle, Supercritical-Pressure Light Water Reactor. In: International Congress on Advances in Nuclear Power Plants; Hollywood, FL, United States; 1993.

7. Oka Y, Koshizuka S, Jervremovic T. Supercritical-Pressure, Light-Water Cooled Reactors for Improving Economic, Safety, Plutonium Utilization and Environment. Progress in Nuclear Energy. 1993;29(103):295-302.

8. Buongiorno J, MacDonald PE. Progress Report for the FY-03 Generation-IV R&D Activities for the Development of the SCWR in the U.S. 2003.

9. Oka Y, Koshizuka S, Ishiwatari Y, et al. Super Light Water Reactors and Super Fast Reactors. USA: Springer; 2010. 416 p. ISBN 978-1-4419-6034-4

10. Shan J, Zhang B, Li C, et al. SCWR subchannel code ATHAS development and CANDU-SCWR analysis Nucl Eng Des. 2009;239:1979-1987.

11. Chaudri KS, et al. Development of sub-channel code SACoS and its application in coupled neutronics thermal hydraulics system for SCWR. Annals of Nuclear Energy. 2012;45(37-45). ISSN 03064549. DOI 10.1016/j.anucene.2012.02.014.

12. Briesmeister JF. A General Monte Carlo N-Transport code, Version 4C.LA-12625. Los Alamos National Laboratory; 1993.

13. Barragán Martínez AM, Martin C FJ. MCNPX and HELIOS 2 comparison for the neutronics calculations of a Supercritical Water Reactor HPLWR. Annals Nuclear Energy. 2013;51:181-188. ISSN 03064549. DOI 10.1016/j.anucene.2012.08.013.

14. Hofmeister J, et al. Fuel assembly design study for a reactor with supercritical water. Nuclear Engineering and Design. 2007;237(14):1513-1521. ISSN 00295493. DOI 10.1016/j.nucengdes.2007.01.008.

15. Castro L, Rojas L, Gamez A, et al. Thermal-hydraulic analysis of heat transfer in subchannels of the European High Performance Light Water-Cooled Reactor for different CFD turbulence models. In: International Nuclear Atlantic Conference. São Paulo, Brazil. ISBN 978-85-99141-06-9.

16. Tulkki V. Supercritical water reactors: A survey on International State of Research in 2006 [Tesis de Maestría]. Otaniemi, Finland: Helsinki University of Technology; 2006.

 

 

Recibido: octubre de 2015
Aprobado: febrero de 2016

 

 

AUTORES

José Angel González Quintero. Ingeniero Electricista. Máster en Ciencias. Doctor en Ciencias Técnicas. Profesor Titular del Centro de Estudios Electroenergéticos (CEE) de la Universidad Central "Marta Abreu" de Las Villas (UCLV), Santa Clara, Cuba. e-mail: [e-mail].