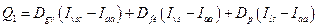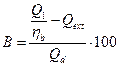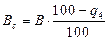Artículo de investigación

Aprovechamiento en una caldera del vapor saturado seco proveniente de fuente externa

Take the advantage in a boiler of dry saturated steam from an external source

0000-0001-9385-6884Alberto E. Calvo-González^{I  *}  , 0009-0001-5420-4725Cesar J. González-Rondón^I  , 0000-0002-2005-4466Luis Aballe-Infante^I  , 0000-0002-6735-6509Danitza María Cortes Perez^II  , 0000-0002-4006-4135José R. Rodríguez Bertrán^III  , 0000-0002-5406-5390Roberto Vizcón-Toledo^IV 

^I Universidad Tecnológica de la Habana “José Antonio Echeverría”, Cujae. La Habana, Cuba

^II Universidad Nacional Abierta y a Distancia UNAD, Bogotá, Colombia

^III Universidad de la Habana. La Habana, Cuba

^IV Universidad de Matanzas, Matanzas, Cuba

RESUMEN

En el siguiente trabajo se realizó el estudio del comportamiento de una caldera de una termoeléctrica en un régimen complejo, fuera de diseño, ya que aprovecha la existencia de una fuente externa de vapor saturado y seco. Este vapor se sobrecalentará en el sistema de sobrecalentamiento del vapor de la misma. El análisis se realizó a partir de la adaptación del modelo del Cálculo Térmico Normativo en el cual se tiene experiencia. Comprobando los resultados del modelo ajustado con los regímenes de carga estipulados, se pasó a calcular el régimen complejo para las cargas máxima y mínima de la turbina y variando el aprovechamiento del vapor externo desde un 20% hasta un 5%, con intervalos de 5%, la sustitución del vapor principal a la turbina. Resultando que el consumo de combustible de la caldera es siempre menor en régimen complejo, que el consumo trabajando de forma habitual.

Palabras-clave: calderas; digitalización; modelación; cálculo térmico normativo; régimen complejo

ABSTRACT

The study of the behavior of a power plant boiler in a complex régime, outside of design, was carried out in this work. Since, it takes the advantage of an external source of dry saturated steam. This steam will be super heated in the super heating system of the boiler. The analysis was based on the adaptation of the Normative Thermal Calculation Model in which there is experience. Checking the results of the adjusted model with the stipulated load regimes, the complex regime was calculated for the maximum and minimum loads of the turbine and varying the use of external steam from 20% to 5%, with intervals of 5%, the replacement of the main steam to the turbine. Resulting in that the fuel consumption of the boiler is always lower in complex regime, than the consumption working normally.

Key words: boilers; digitalization; modeling; normative thermalcalculations; complex regime

Introducción

El poder aprovechar en la caldera de una central termoeléctrica una fuente de calor externa, es sumamente ventajoso, porque contribuye a disminuir el consumo de combustible fósil haciendo más barata la generación eléctrica disminuyendo el índice combustible por kilowatt-hora generado, y por ende, la contaminación atmosférica por gases de efecto invernadero que la combustión de éste produce. Si se tiene disponible un flujo de vapor saturado seco que puede ser aprovechado en la central termoeléctrica y dado sus parámetros, éste puede ser aprovechado en la caldera que alimenta a un turbogenerador.

Cuando a un sistema de generación de vapor se le suministra un flujo de vapor de una fuente externa, entra en la categoría de régimen complejo, debido a que el sistema trabajará fuera de su régimen nominal de operación, para el cual fue diseñado. Se desconoce cómo se comportarían los principales parámetros técnicos de la caldera al incorporarle un flujo de vapor saturado y seco, producido por una fuente externa, a su sistema de sobrecalentamiento del vapor y que después también alimentará a la turbina. Esa es la situación problémica de esta investigación. En la literatura aparecen estudios de regímenes complejos en la generación de vapor. Un estudio en que se pretende aumentar la eficiencia de una central subcrítica de 500MW ^[1], utiliza la combinación de la caldera con el sistema de extracciones regenerativas de la turbina este sistema es complejo.

El vapor extraído se utiliza para elevar la temperatura del aire en el precalentador vapor-aire antes de que el aire se envíe a la caldera. Debido al aumento de la temperatura del aire en la entrada de la caldera, eleva la temperatura de los gases de combustión en la salida de la caldera. El secador de gases de combustión se utiliza para reducir la temperatura de los gases de combustión a 150 ◦C. Al hacerlo, se reduce el contenido de humedad del combustible, lo que da como resultado en un aumento del rendimiento de la caldera y de la eficiencia global de la central eléctrica. En su análisis parte de las limitaciones originales del diseño del esquema térmico convencional, que no permite la inclusión de otro calentador regenerativo adicional ^[2] y de las experiencias ^[3, ⁴, ⁵, ⁶, ⁷, ^8], de la utilización del precalentador de aire alimentado con vapor de extracción y la integración con secador de gases ^[9, ^10].

Utiliza para la caldera un modelo desarrollado en ^[11]. Al final revisa otras formas de llevarlo a cabo ^[12]. El análisis económico resultante es favorable. Otro caso de sistema complejo es el presentado en Modelación dinámica del domo ^[13], usando un enfoque del sistema de identificación no lineal La generación de energía térmica desempeña un papel importante para satisfacer las demandas de energía actuales. Los controles eficientes y económicos de elementos cruciales como la sección de la caldera de vapor, necesitan un mecanismo de control superior para garantizar una mejor eficiencia. La identificación de la dinámica del modelo es una tarea importante debido al fuerte acoplamiento de las variables del proceso, las no linealidades en la dinámica y las restricciones en las entradas de control. Se seleccionaron diferentes condiciones de operación para estimar la dinámica no lineal de la caldera para verificar con las técnicas existentes de Hammerstein ^[14, ¹⁵, ¹⁶, ¹⁷, ¹⁸, ^19] y Wiener ^[20, ²¹, ²², ^23] para estimar la dinámica del domo de la caldera en términos de estructuras de modelos no lineales.

Posteriormente se modificó el marco no lineal para estimar otras no linealidades presentes en el sistema. Como resultado fueron presentadas las respuestas estimadas del modelo para comprobar la dinámica de la caldera. En ^[24], se plantea otro problema complejo, predecir las futuras incrustaciones, que es un tema importante, decisivo, pero difícil, en la conservación de la energía y por lo tanto la reducción de la contaminación ambiental provocada por las termoeléctricas alimentadas con carbón. Esto es debido a la influencia característica que tiene en la eficiencia de transferencia de calor de sus calderas la escoria de la ceniza. Para la predicción de las áreas grises ^[25, ^26], en áreas calientes, se presenta un sistema híbrido basado en descomposición modal empírica de conjuntos complementarios de modelos grises y redes de memoria a corto plazo. Esto se debe a que la serie temporal de los grados de contaminación por cenizas no es lineal ni uniforme.

Los valores proyectados para el factor de limpieza se generaron luego superponiendo las predicciones y los componentes residuales. Los hallazgos experimentales respaldan la precisión y la confiabilidad del modelo y demuestran que el modelo CEEMD-GM-LSTM, funciona muy bien en el pronóstico de la situación de cenizas en la zona calentada. Dada la situación problémica esbozada más arriba se hace imprescindible el disponer de un modelo confiable, probado, con el cual se tenga experiencia en el diseño y evaluación de calderas. Ese modelo fue desarrollado en ^[27], utilizando el modelo establecido en el Cálculo Térmico Normativo de Calderas ^[28, ^29], con el cual se han diseñado y calculado en Cuba muchas calderas de bagazo y también adaptaciones en la industria eléctrica, digitalizando los diagramas y nomogramas de cálculo y utilizando la hoja de cálculo EXCEL.

Entonces el Objetivo general seria: Determinar los principales parámetros técnicos del generador de vapor trabajando en régimen complejo a cargas mínima, de 35MW y máxima de 60MW del turbogenerador. Los otros posibles regímenes complejos estarían comprendidos entre ellos. Para llevar a cabo este objetivo previamente se validó la herramienta de cómputo de ^[27], para todas las cargas establecidas en las cartas de régimen es decir 35; 37,5; 40; 42,5; 50; 55; y 60 MW y se comparó con ellas, con resultados satisfactorios. El Objeto de estudio será la caldera BK-100 que alimenta un turbogenerador de vapor de 60 MW, cuyo corte seccionado aparece en la figura 1.

Sobre la base de las consideraciones publicadas ^[27], se realizó el cálculo de un conjunto de regímenes complejos para el generador de vapor BK-100, los cuales se calcularán para la generación del vapor de la caldera a un 80%, 85%; 90% y 95% y el 100% de la circulación del flujo de vapor para las cargas extremas de la misma 60 MW y 35 MW. En el presente artículo por razones de espacio solo expondrán los cálculos para la potencia máxima de 60 MW y los resultados para la potencia mínima de 35 MW aparecerán entonces sólo en los gráficos resultantes comparativos. En este caso no es necesario repetir el cálculo de combustión ya que se parte del mismo combustible.

El primer aspecto que se determina en el balance térmico es el calor disponible y posteriormente se pasa a la determinación de las pérdidas de calor que puedan presentarse en los GV, los cuales son: pérdidas con los gases de escape, pérdidas por incombustión química, pérdidas por incombustión mecánica, pérdidas de calor al exterior a través de las paredes del GV. Una vez determinada cada una de las pérdidas que puedan presentarse en el GV, se procede a calcular el valor de la eficiencia bruta. Del total de la energía disponible que entra al GV, una parte la conforman las pérdidas de calor y otra parte es realmente aprovechada por la sustancia de trabajo; esta última es el calor útil, el cual se determina a partir de la eficiencia y del calor disponible. Con el calor útil, los flujos de la sustancia de trabajo y el calor disponible se puede determinar el consumo de combustible; a partir del cual debido a las pérdidas por incombustión mecánica, se determina realmente la cantidad de combustible que se quema en el GV. Es necesario calcular el calor útil que utilizará la caldera para producir los 60 MW, o los 35 según sea el caso.

Determinación del calor útil

El calor útil puede ser calculado por la ecuación (1):

(1)

Donde: D_gv es el vapor generado en la caldera para cada régimen llamado complejo, D_fe es el flujo de vapor saturado seco proveniente de fuente externa, D_p es el flujo de la purga continua, I_vsc es la entalpia del vapor sobrecalentado, I_vs es la entalpia del vapor saturado, I_aa es la entalpia del agua de alimentar, I_ls es entalpia del líquido saturado.

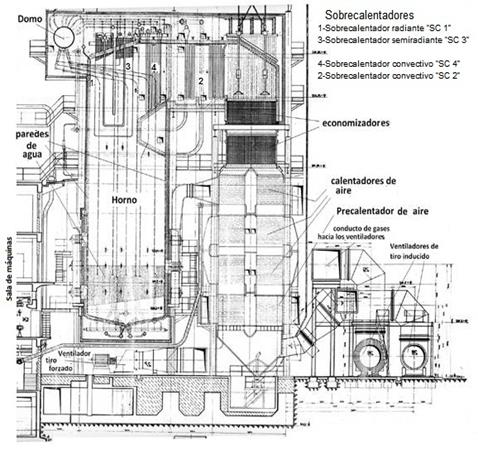
Fig. 1 Corte seccionado de la caldera objeto de estudio que muestra las superficies principales de cálculo 

El cálculo de regímenes complejos, se realizará solamente para los valores extremos de generación, máxima y mínima, del bloque del rango anteriormente empleado, o sea, 60 MW y 35 MW. Los demás quedarán comprendidos entre esos dos extremos. En la tabla 1, se muestran los parámetros necesarios para la determinación del calor útil para 60 MW según el porcentaje aportado por la caldera. Estos datos son: D_total-Flujo de vapor que llega a la turbina, D_gv(kg/s)-Vapor generado en caldera, D_fe(kg/s)-Flujo de vapor de fuente externa, D_p(kg/s)-Flujo de la purga continua, I_aa(kJ/kg)-Entalpia del agua de alimentar, l_s(kJ/kg) -Entalpia del líquido saturado, I_vs(kJ/kg)-Entalpia del vapor saturado, I_vsc(kJ/kg)-Entalpia del vapor sobrecalentado. Los valores del calor útil para cada uno de los regímenes complejos desde el 100%, el 95, 90, 85 y 80% y se muestran en el renglón final de la tabla 1.

Tabla 1 Datos para la determinación del calor útil para 60 MW 

	Porcentaje aportado por la caldera
Parámetros	100%	95%	90%	85%	80%
Dtotal	68,0556	68,0556	68,0556	68,0556	68,0556
Dgv(kg/s)	67,035	63,683	60,331	56,09	53,628
Dfe(kg/s)	0	3,4028	6,805	10,945	13,611
Dp(kg/s)	1,021	0,9698	0,9188	0,8542	0,8167
Iaa(kJ/kg)	877,8	877,8	877,8	877,8	877,8
ls(kJ/kg)	1413,774	1413,774	1413,774	1413,774	1413,774
Ivs(kJ/kg)	2703,41	2703,41	2703,41	2703,41	2703,41
Ivsc(kJ/kg)	3484,86	3484,86	3484,86	3484,86	3484,86
Calor Útil necesario para cada uno de los regímenes complejos para producir 60 MW
Q1(kJ/s)	175109,58	169204,9402	163098,4818	155240,7768	150885,5651

Determinación del Consumo de combustible para cada régimen complejo hasta el 20 % de sustitución

Para calcular el consumo de combustible de cada nuevo régimen es necesario conocer el calor disponible del combustible y la eficiencia bruta del generador de vapor η _b , entonces se determinará por la ecuación (2):

(2)

Calculándose el calor disponible como: Q _d = Q _at + Q _fc +Q _pca + PCI

Donde: Q_d Calor disponible, Q_at es el calor empleado en la atomización del combustible, Q_fc es el calor físico (en función de su temperatura) del combustible, Q_pca es el calor físico (en función de su temperatura) del aire en el precalentador de aire, Q _ext calor recibido de la fuente externa definido como: Q _ext = D _fe (I _vs - I _amb )

El Consumo de combustible quemado o de cálculo, se calcula por la ecuación (3):

(3)

Donde: B es el consumo de combustible para cada regimen complejo, aprovechando la corriente exterior de vapor saturado, q₄ es el calor perdido por la incombustión química, Bc es el consumo de combustible quemado o de cálculo aprovechando la corriente exterior pero considerando q₄. En la tabla 2, se muestran los resultados para el calor disponible Q _d , la eficiencia bruta η, el Consumo de combustible aprovechando la corriente exterior B(kg/s) y Bc(kg/s) teniendo en cuenta la pérdida por incombustión química.

Tabla 2 Consumo de combustible aprovechando corriente exterior según el porcentaje de vapor generado en caldera para producir 60 MW 

	Porcentaje de vapor generado
Parámetros	95%	90%	85%	80%
Q d	42893,48	42894,08	42895,26	42895,66
η	0,89073	0,89225	0,89529	0,8963
B(kg/s)	4,223	3,850	3,381	3,103
Bc(kg/s)	4,097	3,735	3,280	3,01

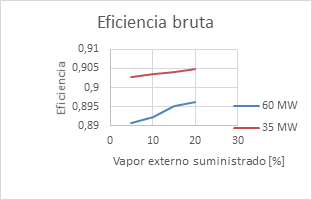
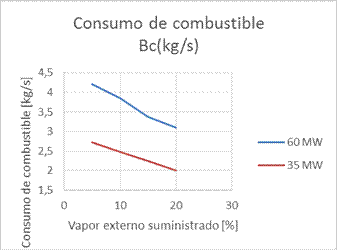
A continuación en la figura 2, se muestra la variación de la eficiencia bruta de la caldera para cada uno de los regímenes complejos calculados para satisfacer la potencia de 69 MW y 35 MW en función del vapor externo aprovechado y en la figura 3, se muestra la variación del consumo de combustible en función también del porcentaje de vapor externo suministrado.

Fig. 2 Eficiencia bruta del generador de vapor en régimen complejo 

Fig. 3 Consumo de combustible en régimen complejo 

Balance térmico del horno

La determinación de las pérdidas de calor en porcentaje para cada uno de los regímenes complejos aparece en la tabla 3, para la potencia de 60 MW, ahí están referidos: q₂-Pérdida de calor con los gases de escape, q₃-Pérdida de calor por incombustión química, q₄ -Pérdida de calor por incombustión mecánica, q₅-Pérdida de calor al exterior a través de las paredes del horno.

Tabla 3 Pérdidas de calor para cada régimen complejo de 60 MW 

	Porcentaje de vapor generado en la caldera
Parámetros	95%	90%	85%	80%
q2(%)	7,073	6,921	6,618	6,516
q 3(%)	0,088	0,088	0,088	0,088
q 4(%)	3,000	3,000	3,000	3,000
q5(%)	0,765	0,765	0,765	0,765

Cálculo térmico del horno

Los resultados del cálculo térmico del horno se muestran en la tabla 4, donde aparecen el Calor absorbido en el horno, Qh(KJ/Kg), la Temperatura adiabática, Ta (K), la Entalpia de los productos de la combustión a la salida del horno, I´´h(KJ/Kg), el Calor especifico medio de los productos a la salida del horno, C´´h (KJ/KgK), la Efectividad térmica promedio en el horno, ψh, la Altura relativa del plano de máximas temperaturas, M (m), la Emisividad de la parte luminosa de la llama, a l, la Emisividad de la parte no luminosa de la llama, a nl, Emisividad de la llama, all, la Emisividad térmica del horno, ah, el Coeficiente de conservación de calor, Ψ, la Temperatura calculada a la salida del horno, T´´ hc (K), la Comprobación del cálculo térmico del horno, ΔT´´h, y la Absorción específica de calor en el horno, Qrh(KJ/Kg).

Tabla 4 Resultados del cálculo térmico del horno para la potencia de 60 MW para cada uno de los regímenes complejos según el porcentaje de vapor generado en caldera 

	Porcentaje de vapor generado
Parámetros	95%	90%	85%	80%
Qh(KJ/Kg)	45161,69	45161,69	45161,69	45161,69
Ta (K)	2113,16	2113,16	2113,16	2113,16
I´´h(KJ/Kg)	25447,66	25058,66	24721,88	24334,07
C´´h (KJ/KgK)	26,21	26,20	26,20	26,19
ψh	0,55	0,55	0,55	0,55
M (m)	0,5	0,5	0,5	0,5
a l	0,788	0,785	0,782	0,779
a nl	0,408	0,412	0,415	0,418
all	0,617	0,617	0,617	0,617
ah	0,745	0,745	0,745	0,745
Ψ	0,9915	0,9915	0,9915	0,9915
T´´ hc (K)	1276,63	1264,91	1248,77	1239,66
ΔT´´h	84,36	81,09	84,23	78,34
Qrh(KJ/Kg)	19546,17	19932,14	20266,65	20651,37

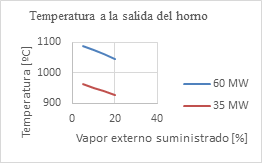
En la siguiente figura 4, aparecen las temperaturas a la salida del horno para cada uno de los regímenes complejos de 80, 85, 90, 95 %

Fig. 4 Temperaturas de salida del horno para cada uno de los regímenes 

Cálculo del sobrecalentador radiante “SC 1”

Los resultados del cálculo del sobrecalentador radiante “SC 1” para las variables: Flujo de vapor por el sobrecalentador de pared “SC1”, D _scp , el incremento de entalpía, ∆i _p, el Calor por balance (calor absorbido por el vapor), Q _b , la Temperatura del vapor T´´v (°C) a la salida para los regímenes complejos para carga máxima de 60MW, se muestran en la sección homónima de la tabla 5.

Cálculo del sobrecalentador semiradiante “SC 3”

Los resultados del cálculo del sobrecalentador semiradiante “SC 3” para la carga de 60MW, son expuestos en la tabla 5 en la sección homónima, donde aparecen los valores del Calor absorbido por el vapor (Q_b), del Calor por radiación (Q _r ), del Calor por convección (Q_c) y del Calor total transferido, Q_t, el Error en el cálculo del calor en porcentaje, ΔQ(%), la Temperatura del vapor, T´´v(°C) y la Temperatura de los gases T´´g(°C).

Cálculo del festón 1

El cálculo del festón 1, realizado para 60 MW, arrojó para las variables Disminución de temperatura, ΔT, la Entalpia de salida de gases I’’_g, el Coeficiente conductividad térmica de los gases, (λ_g), la Densidad de los gases, (γ_g), el criterio o número de Prandtl para los gases, (P_rg), el Calor por convección, Qc, el Calor total por transferencia o transferido, Q_t, el Error cometido en el cálculo del calor ΔQ(%) los resultados expuestos en la sección Cálculo del Festón 1 de la tabla 5.

Cálculo del sobrecalentador convectivo “SC 4”

La tabla 5, en su última sección, muestra los resultados obtenidos del cálculo del sobrecalentador convectivo. “SC 4” para los regímenes complejos, donde aparecen los valores calculados del Flujo de vapor que circula por él, D_sc4, el Incremento de entalpía que ocurre en el SC4, ∆i_sec4, el Calor por Balance que es igual a Qc por convección, el calor por transferencia o transferido, Q_t, el Error en el cálculo del calor, ∆Q (%), la Temperatura del vapor sobrecalentado, T´´vapor (°C), la Temperatura de los gases que se dispone, T´´gases (°C).

Tabla 5 Resultados del cálculo del sobrecalentador radiante. “SC 1”, del sobrecalentador Semiradiante “SC 3”, del Festón 1 y del sobrecalentador convectivo. “SC 4” para cada uno de los Regímenes complejos según el porcentaje de vapor generado en caldera para 60 MW 

Sobrecalentador radiante. “SC 1”
	Porcentaje de vapor generado en caldera
Parámetros	95%	90%	85%	80%
D scp	58,56	58,56	58,56	58,56
Δi p	170,37	167,18	161,25	159,52
Q b	2322,44	2368,30	2408,04	2453,76
T´´v(°C)	344,26	344,26	344,26	344,26
Sobrecalentador Semiradiante “SC 3”
Parámetros	95%	90%	85%	80%
Q b	3324,363	3454,709	3641,930	3751,290
Q r	42,946	45,272	46,439	49,196
Q c	3281,417	3409,437	3595,491	3702,094
Q t	3330,833	3395,799	3547,496	3651,162
ΔQ(%)	1,484	0,419	1,353	1,395
T´´v(°C)	459,749	458,394	457,074	456,685
T´´g(°C)	941,49	920,97	900,13	877,19
Festón 1
Parámetros	95%	90%	85%	80%
ΔT	14	13	12	11,5
I’’g	21704,03	21201,92	20693,71	20120,56
(λg)	0,108076669	0,106053463	0,104019789	0,101772035
(γg)	1,45E-04	1,41E-04	1,37E-04	1,33E-04
(Prg)	0,570433036	0,572988703	0,575616265	0,578589058
Qc	434,433	418,618	402,647	398,500
Qt	427,022	418,201	411,550	401,536
ΔQ(%)	1,75	0,100	2,163	0,756
Sobrecalentador convectivo. “SC 4”
Parámetros	95%	90%	85%	80%
D scc4	67,035	67,035	67,035	67,035
Δi scc4	337,8942	339,968	343,824	344,948
Q b	5272,937	5513,319	5878,031	6074,327
Q t	55238,684	5559,041	5913,047	6060,353
ΔQ(%)	0,654	0,822	0,592	0,231
T´´vapor (°C)	540	540	540	540
T´´gases(°C)	717,31	680,19	644,31	615,98

Cálculo del festón 2

Realizado el cálculo del festón 2 para la potencia de 60MW se muestra en la primera parte de la tabla 6, para cada una de las variables calculadas, a saber el ΔT(ºC) en el equipo, la Entalpía de salida de los gases, I’’g, el Coeficiente de conductividad térmica de los gases, (λg), la Densidad de los gases, (γg), el criterio o número de Prandtl para los gases, (P_rg), el Calor por convección, Qc, el Calor transferido, Qt y el Error en el cálculo del calor, ΔQ(%).

Cálculo del sobrecalentador convectivo “SC 2”

Los valores que arrojan los cálculos del sobrecalentador convectivo “SC 2”, aparecen en la tabla 6, en la sección sobrecalentador convectivo 2 , mostrándose cada valor para cada uno de los regímenes complejos cuyas variables son; D _scc2 -Flujo de vapor en el SC2, Δi _scc2 -Incremento de la entalpía en el SC 2, Q _b -Calor por balance (absorbido), Q _t -Calor por transferencia total, ΔQ(%)-Error en el cálculo del calor, T´´v(°C)-Temperatura del vapor, T´´g(°C)-Temperatura de los gases

Cálculo térmico del economizador

Los resultados del cálculo térmico del economizador aparecen en su sección correspondiente en la tabla 6, donde se muestran: D _eco -Flujo de vapor por el economizador, Q _c -Calor por convección por el lado vapor, Q _t -Calor por transferencia o transferido, ΔQ (%)-Error en el cálculo del calor, T´´ _g (°C)-Temperatura de los gases.

Cálculo térmico del calentador de aire

En la tabla 6, en la última sección, se muestran los valores de: las temperaturas de entrada y salida para cada una de las corrientes, el aire y los gases, el Calor calculado por balance, Q_{b ca}, Calor total por transferencia o transferido, Q_{t ca}, y la cuantificación del Error en cálculo del calor

Tabla 6 Resultados del Cálculo del Festón 2, del sobrecalentador convectivo “SC 2”, del economizador, del calentador de aire para cada uno de los Regímenes complejos según el porcentaje de vapor generado en caldera para 60 MW 

Festón 2
Parámetros	95%	90%	85%	80%
ΔT(ºC)	20	18,5	17	15,5
I’’g	15728,57	15018,81	14179,30	13528,31
(λg)	0,080785466	0,082734919	0,079518654	0,07701264
(γg)	9,39E-05	9,75E-05	9,17E-05	8,72E-05
(Prg)	0,609830831	0,606664099	0,61191756	0,616112445
Qc	655,741	621,334	585,292	545,827
Qt	645,039	612,920	576,773	547,585
ΔQ(%)	1,659	1,373	1,477	0,322
Sobrecalentador convectivo “SC 2”
Parámetros	95%	90%	85%	80%
D scc2	58,556	58,556	58,556	58,556
Δ iscc2	181,943	183,060	185,136	185,741
Q b	2480,148	2593,213	2764,757	2857,086
Q t	2434,338	2604,126	2720,644	2885,168
ΔQ(%)	1,882	0,419	1,621	0,973
T´´v(°C)	390,96	389,77	388,63	388,37
T´´g(°C)	580,93	546,80	504,66	473,56
Economizador
D eco	64,65	61,25	56,94	54,44
Q c	7747,157	7339,411	7239,556	7184,572
Q t	7816,164	7220,791	7200,426	7142,522
ΔQ(%)	0,883	1,643	0,543	0,589
T´´ g (°C)	249,3	231,8	193,0	163,5
Calentador de aire
Aire Entrada T(K)	363	363	363	363
Aire Salida T(K)	473	453	410	373
Gases Entrada T(K)	522,28	504,78	465,96	436,520
Gases Salida T(K)	-	-	-	-
Q bca (kJ/kg)	1910,213	1551,944	788,220	144,821
Q tca (kJ/kg)	1933,032	1544,998	780,379	142,391
ΔQ ca (%)	1,180	0,450	1,005	1,707

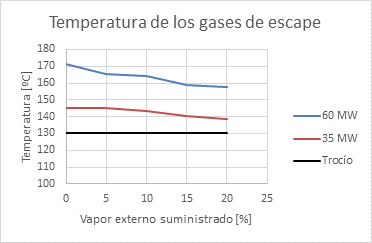
A continuación la figura 5, muestra la comparación de la variación de la temperatura de los gases de escape para los regímenes complejos calculados es decir, como se afecta según el porcentaje de vapor sustituido desde cero al 20%.

Fig. 5 Temperatura de gases de escape en régimen complejo 

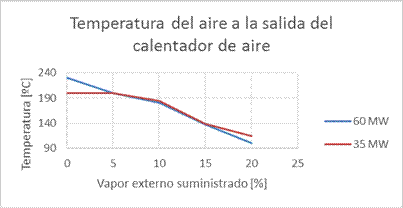
En la figura 6, se muestran la variación de la temperatura del aire a la salida del calentador de aire para cada régimen complejo estudiado, desde ninguna sustitución hasta el 20 por ciento.

Fig. 6 Temperatura del aire a la salida de calentador de aire en régimen complejo 

Discusión y resultados

El consumo de combustible de la caldera es siempre menor trabajando en régimen complejo que el consumo trabajando de forma habitual, para las condiciones de trabajo de diseño a las mismas potencias de entrega. Se aprecia que al trabajar las calderas en régimen complejo, suministrando a la misma entre un 5% y un 20% de vapor saturado y seco desde una fuente externa, la eficiencia térmica de la misma es superior. También se aprecia como disminuye linealmente el consumo de combustible al incrementarse el porcentaje de vapor suministrado por una fuente externa. Se observa una disminución de la temperatura de los gases de escape a la salida del horno al aumentar el suministro de vapor de una fuente externa y al disminuir la potencia del bloque. La temperatura de los gases de escape disminuyó al disminuir la carga del bloque en régimen complejo. Trabajando en régimen complejo, siempre las temperaturas de los gases de escape fueron superiores a la temperatura de rocío ácido para los regímenes analizados según se puede apreciar en la figura 4.

Conclusiones

Se determinaron los principales parámetros técnicos del generador de vapor BK-100 trabajando en diferentes regímenes complejos, es decir aprovechando un flujo de vapor saturado y seco, de una fuente externa, a las cargas mínima, de 35MW y máxima de 60MW del turbogenerador, que por razones de espacio solo expusieron los cálculos para la potencia máxima de 60 MW y los resultados para la potencia mínima de 35 MW, entonces sólo en los gráficos resultantes comparativos. Resultando que el consumo de combustible de la caldera es siempre menor en régimen complejo, que el consumo trabajando de forma habitual. Para llevar a cabo este objetivo previamente se validó la herramienta de cómputo basada en la hoja de cálculo Excel, para todas las cargas establecidas en las cartas de régimen es decir 35; 37,5; 40; 42,5; 50; 55; y 60 MW y se comparó con ellas, con resultados satisfactorios.

Recomendaciones

Efectuar el cálculo hidrodinámico y aerodinámico de la instalación en estos regímenes complejos para conocer su comportamiento y pasar al estudio de factibilidad. Estudiar el mismo fenómeno en otras calderas como la BKZ-340-140/29M

Agradecimientos

Los autores desean agradecer al Ing. Lozeto Casimiro de Armas, especialista en centrales termoeléctricas, sin su colaboración no hubiese sido posible este trabajo. Al Ing. Renier Domínguez Machado cuya contribución fue decisiva, al igual que el Ernesto López-García, a todos muchas gracias.

Referencias

1.  Chantasiriwan S. “Improvement of conventional design of lignite-fired thermal power plant by integrating steam-air preheater and flue gas dryer”. Energy Conversion and Management: X. 2022, vol. 15, e100272. ISSN 2590-1745. Disponible en: https://www.sciencedirect.com/science/article/pii/S25901745220009521.

2.  Akpan PU, Fuls WF. “Generic approach for estimating final feed water temperature and extraction pressures in pulverised coal power plants”. Appl Therm Eng. 2018, vol. 141, p. 257-68. ISSN 1873-5606. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S13594311173814252.

3.  Han X, et al3.  . “Thermodynamic analysis of an improved flue gas pre-dried lignite-fired power system integrated with water recovery and drying exhaust gas recirculation”. Drying Technol. 2020; vol. 38, n. 15, p. 1971-1987. ISSN 1532-2300. Disponible en:https://www.tandfonline.com/doi/full/10.1080/07373937.2019.16078713.

4.  Liu R, Liu M, Yan J. “Techno-economic analysis of the lignite-fired power plant integrated with a steam or flue gas dryer”. Drying Technol . 2021, vol. 39, n. 10, 1271-1284. ISSN 1532-2300. Disponible en: https://www.tandfonline.com/doi/abs/10.1080/07373937.2020.17421484.

5.  Fan C, Pei D, Wei H. “A novel cascade energy utilization to improve efficiency of double reheat cycle”. Energy Convers Manage. 2018; vol. 171, p. 1388-1396. ISSN 1879-2227. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S01968904183070405.

6.  Liu Y, et al6.  . “Thermodynamic analysis of a modified system for a 1000 MW single reheat ultra-supercritical thermal power plant”. Energy. 2018; vol. 145, p. 25-37. ISSN 1873-6785. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S03605442173209726.

7.  Lin X, et al7.  . “Thermo-economic analysis of typical thermal systems and corresponding novel system for a 1000 MW single reheat ultrasupercritical thermal power plant”. Energy . 2020; vol. 201, e117560. ISSN 1873-6785. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S03605442203066787.

8.  Chantasiriwan S. “The improvement of energy efficiency of cogeneration system by replacing desuperheater with steam-air preheater”. Energy Rep. 2020; vol. 6, supplement 9, p. 752-757. ISSN 2352-4847. Disponible en: https://www.sciencedirect.com/science/article/pii/S23524847203156028.

9.  Tang C, et al9.  . “Investigation on a new lignite predrying power generation system combined with a front air heater”. Drying Technol . 2020; vol. 38, n. 12, p. 1584-1596. ISSN 1532-2300. Disponible en: https://www.tandfonline.com/doi/full/10.1080/07373937.2019.16500629.

10.  Chantasiriwan S. “Techno-economic analysis of the integration of flue gas dryer and steam-air preheater into biomass power plant”. Drying Technol . 2022, vol. 40, n. 16. ISSN 1532-2300. Disponible en: https://www.tandfonline.com/doi/full/10.1080/07373937.2022.205118110.

11.  Chantasiriwan S. “Optimum installation of flue gas dryer and additional air heater to increase the efficiency of coal-fired utility boiler”. Energy . 2021; vol. 221, e119769. ISSN 1873-6785. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S036054422100018911.

12.  Chen H, et al12.  . “Improved combustion air preheating design using multiple heat sources incorporating bypass flue in large-scale coal-fired power unit”. Energy . 2019; vol. 169, p. 527-541. ISSN 1873-6785. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S036054421832376412.

13.  Sumalatha, A., et al13.  . “Dynamic modeling of Boiler drum using nonlinear system identification approach”. Measurement: Sensors. 2023, vol. 28, e100845. ISSN 2665-9174. Disponible en: https://www.sciencedirect.com/science/article/pii/S266591742300181213.

14.  Linwei Li, Xuemei Ren, “Adaptive filtering scheme for parameter identification of nonlinear Wiener-Hammerstein systems and its application”, Int. J. Control. 2020, vol. 93, n. 10. ISSN 1366-5820. Disponible en: https://www.tandfonline.com/doi/full/10.1080/00207179.2019.156663414.

15.  Brouri Adil, Laila Kadi, Kenza Lahdachi, Identification of nonlinear systemcomposed of parallel coupling of Wiener and Hammerstein models Asian J. Control. 2022, vol. 24, n. 3, e11521164. ISSN 1934-6093. Disponible en: https://onlinelibrary.wiley.com/doi/abs/10.1002/asjc.253315.

16.  Brouria Adil, et al16.  . “Identification ofHammerstein-Wiener models with hysteresis front nonlinearities”, Int. J. Control . 2022, vol. 95,n. 12, p. 3353-3367. ISSN 1934-6093. Disponible en: https://www.tandfonline.com/doi/full/10.1080/00207179.2021.197216016.

17.  , D Kappatou Chrysoula; Dominik, Bongartz. “Global dynamic optimization withHammerstein-Wiener models embedded”, J. Global Optim. 2022, vol. 84, p. 321-347. ISSN 0925-5001. Disponible en: https://link.springer.com/article/10.1007/s10898-022-01145-z17.

18.  F Le , et al. “Recursive identification of Hammerstein systems with application to electrically stimulated muscle”. Control Eng. Pract. 2012, vol. 20, n. 4, p. 386-396. ISSN 1873-6939. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S096706611100176618.

19.  A Wills, et al. “Identification of hammerstein-wiener models”. Automatica. 2013, vol. 49, n. 1, p. 70-81. ISSN 1873-2836. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S000510981200481519.

20.  A Haryanto, et al20.  “Maximum likelihood identification of Wiener-Hammerstein models”. Mech. Syst. Signal Process. 2013, vol. 41, n. 2, p. 2714-2719. ISSN 0888-3270. Disponible en: https://www.sciencedirect.com/science/article/pii/S147466701639362420.

21.  M, Ławryn´czuk. “Modelling and predictive control of a neutralisation reactor using sparse support vector machine Wiener models”. Neurocomputing. 2016, vol. 205, p. 311-328. ISSN 1872-8286. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S092523121630299521.

22.  K Li, et al22.  . “Hierarchical multi-class classification in multimodal spacecraft data using DNN and weighted support vector machine”, Neurocomputing . 2017, vol. 259, p. 55-65. ISSN 1872-8286. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S092523121730261822.

23.  Tang Y.G., et al. Identification of nonlinear system using extreme learningmachine based Hammerstein model, Commun. Nonlinear Sci. Numer. Simul. 2014, vol. 19, n. 9, p. 3171-3183. ISSN 1878-7274. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S100757041300586823.

24.  Shi, Y., et al24.  . “A hybrid prediction approach for enhancing heat transfer efficiency of coal-fired power plant boiler”, Energy Reports. 2023, vol. 9, supplement 8, p. 658-668. ISSN 2352-4847. Disponible en: https://www.sciencedirect.com/science/article/pii/S235248472300702324.

25.  Zhang Z, Shi Y. Soot blowing optimization of coal-fired boiler based on Gamma accelerated ash accumulation model. J ElectronMeasur Instrum 2020; vol. 34, n. 8, p. 8-14. ISSN 1000-7105 Disponible en: http://jemi.etmchina.com/jemien/article/abstract/20200802?st=article_issue25.

26.  Chen Y, et al. Fractional Hausdorff grey model and its properties. Chaos Solitons Fractals. 2020, vol. 138, e109915. ISSN 1873-2887. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S096007792030315526.

27.  Calvo-González, A. et al27.  . “Cálculo térmico normativo de calderas digitalizado para el análisis de regímenes estacionarios”. Ingeniería Mecánica. Mayo-Agosto 2019, vol. 22, n. 2, p. 100-107. ISSN 1815-5944. Disponible en: https://ingenieriamecanica.cujae.edu.cu/index.php/revistaim/article/view/610/108427.

28.  Кузнецов, М., et al28.  .“Тепловой расчёт кательных агрегатов (Нормативный метод)”. Энергиа. 1973, n. 21. ISSN 0004-7163. Disponibleen: https://lib.kgeu.ru/irbis64r_15/scan/21эл.pdf28.

29.  Нормы. “ТЕПЛОВОЙ РАСЧЕТКОТЛОВ”. НОРМАТИВНЫЙ МЕТОД. 1998, ed. 3, p. 7-256. Disponible en: https://portal.tpu.ru/SHARED/j/JANKOVSKY/education/%D0%9D%D0%BE%D1%80%D0%BC%D1%8B.pdf29.

Recibido: 01 de Mayo de 2024; Aprobado: 14 de Junio de 2024

^* Autor de la correspondencia: [e-mail]

Los autores declaran que no existe conflicto de intereses.

Alberto E. Calvo-González: Diseño de la investigación, recolección de los datos, implementación de los modelos, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Cesar J. González-Rondón: Diseño de la investigación, recolección de los datos, implementación de los modelos, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Luis Aballe Infante: Diseño de la investigación, recolección de los datos, implementación de los modelos, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Danitza María Cortes Perez: Revisión del estado del arte, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Jose R. Rodríguez Bertrán: Revisión del estado del arte, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Roberto Vizcón Toledo: Revisión del estado del arte, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.