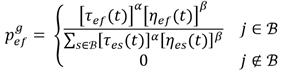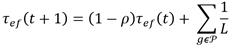Introducción
Los Vehículos Autónomos Terrestres (AGV, Autonomous Ground Vehicles) son sistemas robóticos avanzados diseñados para navegar y operar en tierra sin intervención humana. Estos vehículos utilizan una combinación de sensores avanzados, inteligencia artificial y algoritmos de control para llevar a cabo disímiles tareas, que abarcan desde logística y agricultura hasta defensa y manufactura. La planificación de rutas para un AGV es una tarea de gran relevancia en diversos contextos industriales y logísticos. La eficiencia de esta planificación es esencial, puesto que un diseño de ruta inadecuado puede conllevar a colisiones, daños al equipo y un uso ineficiente de la energía. La literatura científica ha hecho numerosas referencias a esta cuestión [1, 2, 3, 4, 5, 6], subrayando su importancia y su desafío inherente.
Para poder realizar un seguimiento de caminos sin restricciones temporales, el diseño de rutas se enfrenta a dos objetivos fundamentales. El primero es la evasión de obstáculos, que garantiza la seguridad y la integridad física del robot durante su trayecto. El segundo objetivo es minimizar la longitud de la ruta, que contribuye a la eficiencia en términos de tiempo y consumo de energía. Estos dos objetivos confluyen en un problema de optimización.
Para abordar eficazmente este desafío de planificación de rutas, se han desarrollado diversas estrategias, que varían en su nivel de complejidad, precisión y aplicabilidad. Entre estas estrategias, destacan los métodos metaheurísticos, los cuales se derivan de conceptos relacionados con la inteligencia artificial y técnicas estadísticas. Estos métodos ofrecen una perspectiva distinta, al tratar la planificación como un problema de búsqueda donde hay que encontrar, dentro de un amplio espacio de soluciones posibles, aquella solución que optimice ciertos parámetros físicos o alguna combinación de estos.
Para llegar a la solución óptima, los métodos metaheurísticos hacen uso de estrategias de diversificación e intensificación del espacio de búsqueda. La diversificación se refiere a la capacidad para investigar rápidamente zonas del espacio de búsqueda que no han sido consideradas aún. El proceso de intensificación se centra en perfeccionar las soluciones encontradas para incrementar su calidad. El rendimiento del método depende en gran medida de su capacidad para equilibrar estas dos estrategias [7], lo que se logra a través de la selección cuidadosa de los operadores del algoritmo.
A veces, estos métodos pueden tener inconvenientes computacionales, como demasiados parámetros de control, convergencia prematura y tiempo de ejecución elevado [8, 9]. Sin embargo, pueden favorecer un correcto diseño del controlador, evitando cálculos exhaustivos y aportando ventajas como robustez, amplia capacidad de búsqueda global y búsqueda paralela [10].
Este artículo presenta las bases de dos de los métodos metaheurísticos más utilizados en la literatura para resolver problemas de optimización: Algoritmos Genéticos (GA, Genetic Algorithms) [11] y Optimización por Colonia de Hormigas (ACO, Ant Colony Optimization) [10, 12]. En general, estos métodos representan polos opuestos en lo que respecta a su enfoque de búsqueda. GA se caracteriza por adoptar una perspectiva esencialmente determinista, que favorece la intensificación a través de la adaptación gradual de las generaciones al medio ambiente. En contraste, ACO hace amplio uso de la estocasticidad, donde la incorporación de elementos aleatorios o probabilísticos fomenta activamente la diversificación. Estos enfoques, sin embargo, pueden ser modificados a intención del diseñador.
La mayoría de los estudios previos en este tema se centran en evaluar algoritmos para escenarios específicos o bajo condiciones preestablecidas; sin embargo, la particularidad de este trabajo es que adopta un enfoque diferente. Su objetivo principal es comparar los métodos seleccionados en entornos de complejidad variable, lo que permite identificar las situaciones donde cada uno exhibe un desempeño óptimo. Esta perspectiva ofrece una comprensión más completa y aplicable de cómo estos algoritmos pueden ser utilizados en diferentes contextos, lo que potencialmente impulsará avances significativos en la eficiencia y seguridad de las operaciones robóticas autónomas.
El artículo examina el rendimiento de los métodos presentados en módulos de planificación de rutas formadas por tramos rectos, basándose en experimentos simulados.
Metodología
Modelo del ambiente
Para llevar a cabo la planificación de rutas de manera efectiva, es esencial contar con un modelo del entorno en el que los AGV operarán o, en su defecto, tener la capacidad de estimarlo con precisión. Existen diversas representaciones posibles del entorno y, en este contexto, se opta por un mapa de cuadrícula bidimensional [13]. En este modelo, el entorno se describe mediante una imagen cenital que se traduce en una matriz de valores binarios, como se ilustra en la Fig. 1. La complejidad del entorno está determinada por la cantidad y distribución de los obstáculos, pues un terreno que requiere más maniobras evasivas se considera más complejo de navegar.
Una ruta se define, entonces, como un conjunto finito de celdas accesibles conectadas en el mapa de cuadrícula. Matemáticamente, se representa mediante un vector que contiene las coordenadas de las celdas extremas de los segmentos de la ruta, también conocidas como nodos.
Los siguientes epígrafes describen la teoría implementada en cada método metaheurístico seleccionado.
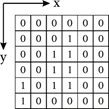
Figura 1 Representación en cuadrículas de una imagen cenital del ambiente, donde “ceros” denotan áreas libres y “unos” indican obstáculos.
Algoritmos genéticos
Un Algoritmo Genético es una técnica de optimización y búsqueda basada en principios inspirados en la evolución biológica [14, 15, 16]. Su base teórica se deriva de la teoría de la evolución de Darwin, donde las soluciones a un problema se representan como “cromosomas” que codifican posibles soluciones. Estos cromosomas son sometidos a procesos que simulan la reproducción, mutación y selección natural para generar mejores soluciones en cada generación.
En su funcionamiento, un conjunto inicial de soluciones candidatas, conocido como población, se crea aleatoriamente. Luego, en cada iteración, las soluciones se evalúan en función de un criterio objetivo, y se seleccionan para reproducirse proporcionalmente a su aptitud. El criterio utilizado para la evaluación de las soluciones se muestra en la Ecuación 1.
Esta expresión algebraica se compone de dos partes. l representa la longitud total del camino que se genera y c, la cantidad de colisiones ocurridas a lo largo del recorrido. ω l > 0 y ω c > 0 son pesos que indican la prioridad de cada uno de estos elementos en la evaluación general de la solución. F sol debe minimizarse con el paso de las generaciones para alcanzar los objetivos de optimización.
Una vez seleccionadas las parejas de soluciones padres se produce la recombinación genética, que simula la reproducción (sexual o asexual, en dependencia del operador de cruce CROSS). En este punto se combinan las características de dos soluciones seleccionadas para producir una descendencia, en la Fig. 2 se muestra el esquema de cruce sexual empleado en este trabajo. En menor medida, la descendencia sufre cambios aleatorios mediante la mutación.
El proceso se repite generación a generación hasta que la producción de nuevos cromosomas arroje una solución adecuada.
Los GA se caracterizan por una serie de parámetros clave que influyen en su rendimiento. Estos incluyen el tamaño de la población (N), que determina cuantas soluciones se mantienen en cada generación; la tasa de mutación (MUT), que regula la probabilidad de que una solución sufra cambios aleatorios; y el operador de selección (SEL), que define como se eligen las soluciones para la reproducción. La elección de estos parámetros y operadores puede afectar significativamente el comportamiento del algoritmo y su capacidad para converger hacia soluciones óptimas.

Figura 2 Esquema de recombinación que ilustra la división de cromosomas parentales en un punto y la formación de cromosomas hijos mediante la unión de sus fragmentos, garantizando la herencia de características de ambos padres.
Algoritmos genéticos modificados. Ga+
Habitualmente se complementan las operaciones de reproducción con otras operaciones, llamadas operaciones de remplazo, con la finalidad de mejorar el comportamiento de los valores de evaluación a través de las iteraciones. Dos modificaciones se proponen en este artículo:
Elitismo: Es usual en GA incluir procedimientos que funcionen como un “ancla” para las mejores soluciones de la población. Como el método utilizado para el proceso de selección incluye cálculo de probabilidades, existe una posibilidad real de que el mejor individuo de una generación se pierda y no forme parte de la siguiente. Para evitar lo anterior se impone, en la población generada, el remplazo de los peores individuos descendientes por los mejores padres, siempre y cuando los padres posean mayor aptitud que los hijos que se remplazan [17].
Migración: Cada vez que se crea una nueva generación, un parámetro MIG regula la inclusión de nuevos individuos generados al azar. Los individuos inmigrantes remplazan a los de peor evaluación, si resultan ser más aptos que estos últimos. La migración se utiliza para aumentar aún más de diversidad de la población y evitar el estancamiento del algoritmo [18].
La estrategia resultante de incorporar estas operaciones de remplazo es conocida como GA+ (Genetic Algorithms plus).
Optimización por colonia de hormigas.
La Optimización por Colonia de Hormigas es un método de búsqueda heurística perteneciente a la familia de la inteligencia de enjambre, inspirado en el comportamiento de búsqueda de alimento de las hormigas en la naturaleza [19, 20]. En su búsqueda de alimentos, las hormigas depositan feromonas y ajustan sus movimientos basándose en la concentración de feromonas en su entorno. Aquellas hormigas que encuentran la ruta más corta hacia el alimento regresan al nido rápidamente, lo que aumenta la cantidad de feromonas depositadas en ese camino. Con el tiempo, este proceso elimina las rutas más largas y guía a las hormigas hacia el camino más corto. De manera análoga, ACO emplea M hormigas artificiales para navegar desde la ubicación inicial del vehículo hasta su destino, evitando obstáculos y modificando un mapa de feromonas artificiales en el proceso. Después de múltiples iteraciones, la distribución de feromonas en el mapa orienta a todas las hormigas hacia la solución óptima.
Cada hormiga puede moverse en un máximo de ocho direcciones, correspondientes a las celdas vecinas, mientras que el movimiento no provoque colisiones o choques con los extremos del mapa. En la iteración t, la hormiga g se traslada desde su celda actual e a una celda f según una regla de probabilidad de transición detallada en la Ecuación 2. En esta ecuación, τ ef (t) representa la concentración de feromonas entre e y f y, η ef (t) es una función heurística que refleja la conveniencia del movimiento hacia f. α y β son coeficientes del algoritmo, que determinan la influencia relativa del rastro de feromonas y de la información heurística, respectivamente. B representa el conjunto de todos los nodos candidatos para los que la hormiga tiene una oportunidad real de trasladarse.
Después de que todas las hormigas completen su ciclo, los niveles de feromonas se disipan gradualmente y se renuevan mediante la Ecuación 3. El coeficiente ρ controla la tasa de disipación (0 < ρ < 1), y P comprende todas las hormigas que pasaron por el segmento e - f. La contribución de feromonas de la hormiga g al segmento es inversamente proporcional a la longitud total del camino (L).
El algoritmo finaliza después de IT max iteraciones.
Optimización por colonia de hormigas modificada. IACO.
ACO suele involucrar operaciones matemáticas complejas que pueden afectar de manera negativa su rendimiento. Se han desarrollado versiones mejoradas del algoritmo para simplificar estas operaciones. Este artículo introduce las siguientes modificaciones clave:
Simplificación del Mapa de Feromonas: Usualmente, el mapa de feromonas se representa como una matriz multidimensional basada en los segmentos potenciales que las hormigas pueden atravesar. Sin embargo, se puede simplificar transformándolo en una matriz bidimensional del tamaño del modelo del ambiente, donde la notación τ ef (t) se reduce a τ f (t) [21].
Paso de Longitud Libre: ACO originalmente establece la longitud de paso como la distancia entre celdas adyacentes, lo que limita las opciones de movimiento y reduce la velocidad de convergencia. Para superar estos desafíos, se adopta la noción de paso de longitud libre [22]. En lugar de restringir el movimiento a celdas adyacentes, las hormigas pueden realizar movimientos más extensos determinados por un valor rv, que representa la extensión de cierto entorno llamado rango visual, como se muestra en la Fig. 3. La función heurística η ef (t) se ajusta en consecuencia, premiando movimientos que se acerquen al destino.

Figura 3 La hormiga se puede desplazar en las direcciones permitidas dentro de la circunferencia o rango visual, evitando obstáculos (celdas negras) y áreas bloqueadas (celdas grises).
El algoritmo resultante de incorporar estas adaptaciones es conocido como IACO (Improved Ant Colony Optimization).
Resultados y discusión
Para evaluar la eficacia de los algoritmos en la planificación de trayectorias, se llevan a cabo experimentos simulados utilizando la herramienta de software Matlab. Las variables seleccionadas para evaluar el rendimiento son el tiempo total de ejecución hasta que se alcanza una ruta adecuada y el valor alcanzado de longitud de la ruta.
Los métodos de optimización se ejecutan 500 veces en tres escenarios diferentes para evitar la aleatoriedad en los datos. Los escenarios difieren en la cantidad de obstáculos y en las distribuciones que presentan:
Escenario 1: Este entorno es el menos complejo de los tres utilizados y consta de un solo obstáculo.
Escenario 2: Este entorno tiene una complejidad moderada y presenta cinco obstáculos con formas regulares.
Escenario 3: En este entorno, aumenta tanto la cantidad de obstáculos como su complejidad geométrica. Presenta ocho obstáculos con diversas formas.
Cada uno de estos entornos se modela como un mapa de celdas de 100×100. El vehículo inicia su trayectoria cerca de la esquina superior izquierda del terreno y finaliza cerca de la esquina inferior derecha.
La calibración inicial de los parámetros de diseño se realiza de acuerdo con las pautas establecidas en la bibliografía [22, 23]. A partir de ahí, se ajustan mediante procedimientos empíricos. En la Tabla 1se muestran los parámetros seleccionados.
Tabla 1 Parámetros de diseño seleccionados para los algoritmos.
| GA+ | IACO | ||||||
|---|---|---|---|---|---|---|---|
| Esc. 1 | Esc. 2 | Esc. 3 | Esc. 1 | Esc. 2 | Esc. 3 | ||
| N | 300 | 500 | 4000 | M | 20 | 20 | 20 |
| SEL | 3 | 3 | 30 | It
|
50 | 50 | 50 |
| CROSS | 0.8 | 0.8 | 0.8 | rv | 25 | 25 | 25 |
| MUT | 0.05 | 0.05 | 0.050 | α | 1 | 1 | 1 |
| MIG | 0.1 | 0.1 | 0.1 | β | 6 | 6 | 6 |
| ω
|
1 | 1 | 1 | ρ | 0.3 | 0.3 | 0.3 |
| ω
|
0.0001 | 0.0001 | 0.0001 | ||||
La Fig. 4 muestra la mejor trayectoria generada por cada algoritmo en los tres escenarios discutidos.
De acuerdo con los resultados de longitud óptima mostrados en la Tabla 2, ambos algoritmos tienen la capacidad de minimizar correctamente la distancia si se permite un número suficientemente grande de iteraciones. Sin embargo, la propuesta de GA+ proporciona trayectorias generadas con longitudes más cortas que IACO.
Tabla 2 Parámetros de diseño seleccionados para los algoritmos.
La Fig. 5 es una presentación gráfica de los datos de longitud en diagramas de violín. Un diagrama de violín se utiliza para visualizar la distribución de los datos y su densidad de probabilidad. Es particularmente útil para interpretar muestras en las que puede existir asimetría estadística, pues disminuye en el análisis la influencia de valores atípicos. La forma característica de este tipo de gráficas muestra la distribución de densidad de los datos [24]. En cada diagrama, el intervalo intercuartil de la muestra (Q3 - Q1) se representa por una sombra dentro del cuerpo de la campana y se interpreta como una medida visual de la dispersión del conjunto de datos. Un segmento recto indica el valor de la mediana de la muestra, que corresponde al segundo cuartil registrado (Q1).
En primer lugar, es esencial señalar algunos datos atípicos generados por IACO en el primer escenario y por GA+ en el segundo escenario, que justifican la utilización de los diagramas de violín para el análisis. Estos valores extremos afectan negativamente los valores de distancia media y desviación estándar.
En el Escenario 1, IACO proporciona distancias más largas y una mayor dispersión de datos. En el diagrama, la mediana y los valores máximos de IACO son iguales, lo que implica que aproximadamente el 50% de las ejecuciones devuelven soluciones más grandes. Por otro lado, GA+ presenta valores más bajos de media, mediana y dispersión de la muestra.
En el segundo escenario de evaluación, IACO continúa generando rutas planificadas más extensas y presenta una desviación cuartil más alta. En contraste, GA+ muestra un rendimiento más eficaz en la reducción de la longitud de la trayectoria, logrando una distancia media de 170.433 unidades y una desviación cuartil de 0.853 unidades. Estos valores estadísticos representan una disminución del 6.7% y del 71.9% en comparación con los respectivos valores obtenidos por IACO. Nótese que el comportamiento de GA+ es particularmente favorable: la moda de la muestra se encuentra en el primer cuartil de la distribución lo que implica que tiende a generar menores datos de distancia para este entorno.
IACO exhibe, una vez más, los valores más altos en las tendencias estadísticas en el Escenario 3. La longitud media de las trayectorias generadas por IACO es de 199.906 unidades, lo que representa un aumento del 8.7% en comparación con la longitud media producida por GA+. Estos hallazgos resaltan las diferencias significativas en el desempeño de ambos algoritmos en entornos de complejidad creciente.
El hecho de que IACO converja hacia valores de longitud mayores que GA+ no debe asociarse a la presencia de un mínimo local que el algoritmo no pueda superar. Las gráficas de la Fig. 5 presentan características unimodales en la distribución de datos, sugiriendo que no existe tal mínimo local. Esta diferencia puede ser el resultado de otros factores que reducen la movilidad de las hormigas, como son las restricciones impuestas en las direcciones de movimiento.
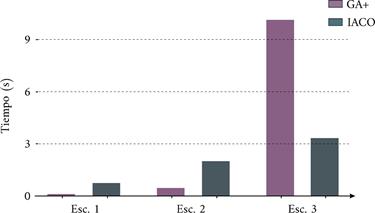
Un retraso excesivo por parte del módulo de planificación de trayectorias puede influir negativamente en el rendimiento y la estabilidad de los módulos de control subsiguientes implementados en el vehículo. Por lo tanto, llevar a cabo un análisis del tiempo de ejecución es esencial. La Fig. 6 contiene una representación gráfica de los datos de tiempo de la Tabla 2.

Figura 5 Comparación de longitudes de ruta obtenidas para los escenarios considerados. Los perfiles de violín representan la distribución de las longitudes en unidades de celdas que ocupan (u), con campanas orientadas hacia arriba para GA+ y hacia abajo para IACO.
IACO muestra un tiempo medio de ejecución más alto en entornos más simples, lo cual es esperado debido a que las probabilidades de selección de nodos implican numerosas operaciones computacionales en cada iteración. Por otro lado, IACO utiliza solo trayectorias libres de colisiones para la búsqueda, tratando los dos objetivos de planificación de manera separada. Este enfoque, en general, perjudica el tiempo de ejecución, pero le proporciona robustez ante cambios en la complejidad de la trayectoria. Nótese el comportamiento casi lineal que exhibe el aumento del tiempo de ejecución al complejizarse el escenario.
Por su parte, el rendimiento de GA+ en términos de tiempo medio de ejecución se degrada significativamente a medida que el entorno se vuelve más complejo. En el Escenario 3 GA+ se ejecuta, en promedio, quince veces más lento que en el Escenario 2 y trescientas setenta y ocho veces más lento que en el Escenario 1. Esto se debe a que GA+ incluye los dos objetivos de control en la función de evaluación. Por lo tanto, la expansión de las áreas de obstáculos aumenta el número de soluciones inválidas y dificulta la búsqueda de soluciones. Esto produce un mayor gasto de tiempo y recursos.
Cuando se trata de entornos complejos, es esencial tener en cuenta tanto la precisión requerida por la misión como la dinámica del sistema de guía y control. En términos generales, se observa que el aumento en el tiempo de ejecución en GA+ es significativamente mayor que la reducción en la distancia lograda en comparación con IACO. Por lo tanto, es recomendable el uso de IACO en la planificación de trayectorias para entornos complejos, a menos que los requisitos específicos de la misión indiquen lo contrario.
Conclusiones
La tarea de planificación de trayectorias para un Vehículo Terrestre Autónomo (AGV) implica minimizar la longitud del recorrido y evitar obstáculos. Este artículo realiza una comparación entre dos métodos metaheurísticos para resolver el problema de planificación de trayectorias en un escenario bidimensional. Se utiliza un método de cuadrícula para modelar el entorno y se llevan a cabo diversas simulaciones en terrenos operativos variados. Al estudiar las estrategias de optimización, se observa que las técnicas metaheurísticas pueden adaptarse con éxito para encontrar una ruta óptima. Sin embargo, los experimentos demuestran que, en comparación con IACO, GA+ funciona mejor en la búsqueda de soluciones en escenarios de complejidad menor o media. A medida que aumenta la zona de obstáculos, el rendimiento mencionado anteriormente se deteriora rápidamente; por lo tanto, IACO es preferible en escenarios altamente complejos.