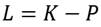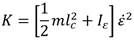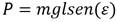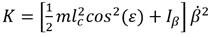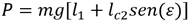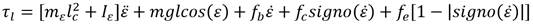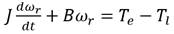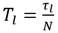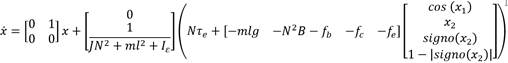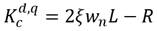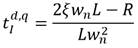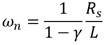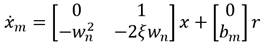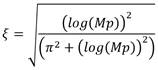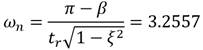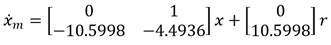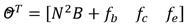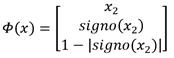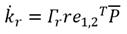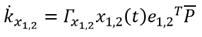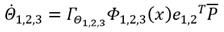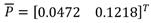Artículo de investigación

Diseño e implementación del control de posición adaptativo para brazo robótico industrial

Design and implementation of an adaptive position control for industrial robotic arm

0000-0003-2675-3476Yordany Vélez Rodríguez^{1  *}  , 0000-0002-7201-5514Jorge H. Vázquez Leiva¹  , 0000-0003-4897-1618José E. Vargas Fernández¹ 

¹ Centro de Investigación y Desarrollo de la Electrónica, Mecánica y Automática “CID MECATRONICS”, La Habana, Cuba

RESUMEN

El presente trabajo tiene como objetivo diseñar e implementar un control adaptativo en unión al control vectorial, con cambios en las dinámicas deseadas para el posicionamiento de los brazos robóticos de dos grados de libertad. El modelo dinámico se obtiene de aplicar el método de Euler-Lagrange en conjunto con el de un motor síncrono de imanes permanentes en el marco de referencia DQ sincrónico. Es diseñado un controlador adaptativo por modelo de referencia que genera el torque referencial para el control vectorial del motor eléctrico. La estabilidad del sistema en lazo cerrado es garantizada al aplicar el método de Lyapunov en las leyes adaptativas. La estrategia de control se implementa en el procesador TMS320F28335 empleando las herramientas MATLAB y Code Composer. Los resultados de las pruebas experimentales son comparados con el esquema de control original obteniéndose un sistema con menores errores dinámicos.

Palabras-clave: brazo robótico; control adaptativo; motor síncrono; control PI

ABSTRACT

The objective of this work is to design and implement an adaptive control in conjunction with vector control, with changes in the desired dynamics for the positioning of two degrees of freedom robotic arms. The dynamic model is obtained by applying the Euler-Lagrange method in conjunction with that of a permanent magnet synchronous motor in the synchronous DQ reference frame. An adaptive controller is designed by reference model that generates the reference torque for the vector control of the electric motor. The stability of the closed-loop system is guaranteed by applying the Lyapunov method in the adaptive laws. The control strategy is implemented on the TMS320F28335 processor using the MATLAB and Code Composer tools. The results of the experimental tests are compared with the original control scheme, obtaining a system with lower dynamic errors.

Key words: robotic arm; adaptive control; synchronous motor; PI control

Introducción

En el país existen brazos robóticos industriales de la década del 60 y 70, cuyos mandos de fuerza de seguimiento sincrónicos emplean elementos obsoletos como amplidinas, amplificadores eléctricos valvulares y motores de corriente directa vinculados estrechamente a una exactitud de seguimiento por posición con errores dinámicos menor o igual a 35 '. Por otra parte, los parámetros físicos del sistema han sufrido variaciones ocasionado por el prolongado tiempo de explotación y modificaciones estructurales, como consecuencia, lograr el ajuste del dispositivo de control y por ende la disponibilidad técnica se torna cada vez más complejo. Esta situación se agrava por la diversidad de tipos de sistemas en existencia, que no solo difieren en peso y dimensiones, sino además, en las dinámicas sujetas a aplicaciones para lo que son empleados. Surge así la necesidad de sustituir los esquemas actuales de regulación automática a partir de técnicas avanzadas de control automático.

Existen diversas técnicas de control que son aplicadas a los brazos robóticos tal como PID ^[1, ², ^3], la lógica difusa ^[4, ⁵, ^6], adaptativos autoajustables ^[7, ⁸, ⁹, ^10], entre otros. Su análisis y diseño requiere del modelo matemático que describe la dinámica de la planta y puede ser obtenido por diferentes métodos abordados ampliamente en ^[11, ¹², ¹³, ^14]. En los trabajos ^[14, ¹⁵, ¹⁶, ¹⁷, ¹⁸, ^19] se evidencian las ventajas matemáticas de aplicar el método Euler-Lagrange. Los modelos que se obtienen presentan inexactitudes y por ello los controladores PID clásicos frente a perturbaciones externas en los límites de las linealidades del sistema tienden a fallar. En ^[17], recientemente se propone el control de modo deslizante de orden fraccionario con operador Koopman para resolver las incertidumbres del modelo, que en comparación con los controles clásicos y los de modo deslizantes de orden fraccional resulta ser superior en cuanto a error de trayectoria, además de presentar una reducción de las señales de control y ser novedoso, solo es demostrado a nivel de simulación y su implementación aún no ha sido alcanzada.

En cuanto a implementaciones recientes que proponen una solución a las inexactitudes están ^[20, ^21] las cuales emplean redes neuronales para crear visión artificial a partir de cámaras y control clásico. La principal ventaja es que obtiene un controlador adaptativo para cualquier brazo robótico, pues la dinámica del sistema se describe por la red neuronal entrenada a partir de imágenes captadas. La capacidad de cómputo requerida es mayor en comparación con técnicas más tradicionales como las adaptativas por modelos de referencias o autoajustables. La implementación de ^[20, ^21] para sistemas con dinámicas elevadas resulta más complejo y tiende a empeorar la exactitud.

El diseño de observadores de estado es una solución a las imprecisiones, en ^[22] se presenta uno extendido para estimar los valores angulares de cada eslabón y los términos de par gravitacional, vector de Coriolis, fricciones y perturbaciones externas. La ventaja que presenta es la reducción de costos al no emplear sensores de posición pues no solo estima los parámetros imprecisos sino los valores de las variables de salida, pero la estabilidad del sistema en lazo cerrado no fue demostrada.

Los controladores adaptativos suelen ser atractivos para los brazos robóticos que exigen errores dinámicos inferiores a los 35 ', pues sin numerosas operaciones matemáticas pueden seguir una referencia deseada ante perturbaciones externas, variaciones de la carga y/o parámetros del sistema, entre otros. Cuando es requerido el cambio de dinámica para una trayectoria dada es más conveniente el control adaptativo por modelo de referencia, ya sea con modelos matemáticos empíricos ^[9, ²³, ^24] o redes neuronales ^[25, ^26]. En ^[25] se emplea una red neuronal con funciones de base radial, que se entrena a partir de los datos de entrada, tensiones de actuadores y datos de salida. A diferencia de ^[20, ^21] el uso de sensores garantiza exactitud, pero el proceso de obtención de las tensiones del actuador para el entrenamiento de la red neuronal es engorroso y depende mucho de la estructura del sistema, por tanto, no es una solución amigable al problema de control. Es en ^[7] donde se aprecia una solución sin procedimientos matemáticos complejos para resolver las inexactitudes del sistema, a pesar de ser desarrollado para un robot móvil ofrece una metodología que garantiza estabilidad en lazo cerrado, y actualización en línea de los coeficientes del controlador con estimación de parámetros por mínimos cuadrados. La vía de estimación de parámetros en ^[7] es adecuada para los controladores adaptativos autoajustables pero los cambios de dinámicas no preestablecidas tienen mejor solución en la aplicación de modelos de referencia ^[9].

En todos los trabajos relacionados con los brazos robóticos la variable de entrada es el torque aplicado a cada eslabón, y como salida el vector de posición y velocidad. Pocos desarrollos hacen mención directa del accionamiento del sistema y los que tratan el tema como en ^[1, ⁴, ²¹, ^27] hacen uso de motores de paso o motores de corriente directa. Las soluciones propuestas en estos casos son viables en aplicaciones de bajas potencias.

En la industria es generalizado el uso de motores de corriente alterna en aplicaciones de mediana y alta potencia, con método de control en tendencia a la aplicación del “control vectorial” o “campo orientado”, ya que ofrece mayores dinámicas y mejor eficiencia energética. La implementación del control vectorial en conjunto con controles difusos ^[28], adaptativos por métodos directos e indirectos ^[29], están encaminados a la optimización de las máquinas eléctricas. Al realizar un análisis del modelo matemático de un motor síncrono de imanes permanentes en el marco de referencia sincrónico DQ ^[30, ³¹, ^33] se puede observar la relación directa de la corriente en cuadratura (iq) con el torque eléctrico lo que sugiere un controlador con dos lazos de control interno para las corrientes del motor, y un lazo externo para generar el par de referencia de cada eslabón a partir de la dinámica deseada, por lo que el presente trabajo tiene como objetivo diseñar e implementar un algoritmo de control adaptativo en unión al control vectorial, con cambios en las dinámicas deseadas para el posicionamiento de los brazos robóticos.

El aporte fundamental del presente trabajo está en el diseño e implementación de un controlador de posición adaptativo por modelo de referencia en conjunto con el control vectorial de los motores síncronos de imanes permanentes que mejora la dinámica de la planta, por lo que es superior al controlador original. Además, se obtiene el modelo matemático del brazo robótico que describe dinámica por el método de Euler-Lagrange.

El presente trabajo se ha estructurado de la siguiente forma: en la sección 2 es desarrollado el proceso de obtención del modelo dinámico por el método de Euler-Lagrange, y se representa como dos modelos en el espacio de estado para facilitar el diseño del controlador. La sección 3 se conforma por dos subsecciones en las que se diseñan los lazos de control internos (subsección 3.1) y el lazo de control externo (subsección 3.2) que implica en si el control adaptativo. En la sección 4 es tratada la implementación del controlador obtenido y en la sección 5 se discuten los resultados. Finalmente se arriban a conclusiones en la sección 6.

Modelado dinámico por método euler-lagrange.

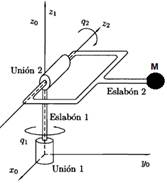
El manipulador robótico objeto de estudio, presenta una estructura como la mostrada en la Fig. 1, y tiene dos articulaciones rígidas con movimiento rotacional, por lo que aplicar el método Euler-Lagrange es sistemático a partir de la ecuación (1).

Figura 1 Estructura de la plataforma giratoria. 

(1)

El par o fuerza representado por τ es generado por el motor eléctrico y F(q ˙,f_e ) es el vector de fuerzas opuestas. En el presente trabajo se emplea el modelo de fricción di námica tratado en ^[8], con tres de sus características (estática, coulomb y viscosa) por tratarse de cuerpos rígidos y además, por la facilidad de análisis dinámico de las velocidades y aceleraciones. El lagrangiano L de todas las energías presentes en el sistema es igual al par o fuerza que las originó y se obtiene por la ecuación (2).

(2)

La energía cinética (K) y la potencial (P) debido a la fuerza de gravedad (g) para el plano vertical es representada por las ecuaciones (3) y (4) respectivamente, y se obtienen teniendo en cuenta la localización del centro de masa (l_c) de la articulación y su masa (m).

(3)

(4)

Y las ecuaciones (5) y (6) para el plano horizontal:

(5)

(6)

Sustituyendo las ecuaciones (3), (4), (5) y (6) en la ecuación (2) para cada plano, y resolviendo (1) se obtiene el modelo matemático de la plataforma en el plano vertical:

(7)

Y para el plano horizontal:

(8)

Los coeficientes de fricción estática (f _e ), de coulomb (f _c ) y viscosa (f _b ) en las ecuaciones (7) y (8) aparecen al tener en cuenta el vector de fuerzas opuestas 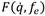. El torque de la carga τl se sustituye en la ecuación (9) que representa la parte mecánica del motor, en la que se tiene en cuenta el coeficiente de fricción del motor (B), momento de inercia (J) y la relación de transmisión (N) entre la articulación y el eje del motor.

(9)

(10)

Con fines al diseño del controlador adaptativo se toma como variables de estado la posición y velocidad articular 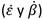, y se llega al modelo siguiente representado en el espacio de estado para el plano vertical:

(11)

y para el plano horizontal:

(12)

Se observa en las ecuaciones (7) y (8) una dependencia del plano vertical en el horizontal. El modelo obtenido se presenta como un sistema estable por naturaleza. En simulaciones realizadas con valores supuestos, fundamentalmente la masa de los cuerpos (aproximadamente una tonelada) se obtiene un valor de torque promedio de 5.64 Nm y picos máximos de 16.3 Nm.

Diseño del controlador adaptativo

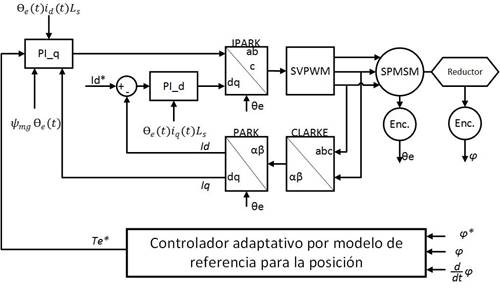
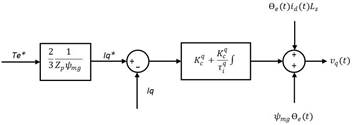
La solución propuesta (Fig. 2), consiste en el control vectorial de un motor acoplado al reductor de fuerza en el que se encuentra un encoder absoluto para la posición de la articulación. Al esquema de control vectorial básico se le sustituyen los reguladores clásicos PID de posición y velocidad, por un controlador adaptativo por modelo de referencia que genera el torque demandado por la carga teniendo en cuenta la dinámica deseada. El par en la unión es procesado para obtener la corriente en cuadratura de referencia iq* que se presenta como entrada al controlador PI correspondiente. Para alcanzar una mayor eficiencia con altos valores de torque, se emplea el método de máximo torque por ampere ^[33, ^34] lo que define como corriente directa de referencia id* constante e igual a cero.

Figura 2 Esquema de control diseñado. 

Control de corrientes dq

Para el control de las corrientes se realiza el procedimiento de compensación de avance no lineal tal como en ^[34] obteniendo así un sistema de primer orden para la parte eléctrica del motor, por lo que un controlador PI garantiza un error de estado estable dada una señal de referencia ^[35]. Los empleados en la propuesta se muestran en las figuras siguientes: para el eje-d Fig. 3 y el eje-q Fig. 4.

Figura 3 Esquema del controlador PI para corriente del eje D. 

Figura 4 Esquema del controlador PI para corriente del eje Q. 

Las ganancias proporcionales y las constantes de tiempo de integración para ambos controladores son idénticas debido a la igualdad entre Ld y Lq por tratarse de un motor síncrono con imanes montados en la superficie del rotor.

(13)

(14)

Por diseño se selecciona un factor de amortiguamiento ξ=0.707. Para el cálculo de la frecuencia natural no amortiguada (ωn) se emplea la ecuación:

(15)

Con γ=0.9 para alcanzar un rendimiento satisfactorio ^[35]. A partir de los datos del motor ofrecidos por el fabricante se obtiene Kc=14 y τ=1.2.

Diseño del controlador adaptativo

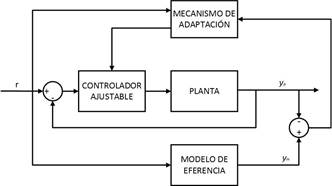
La estrategia de control de posición diseñada para cada articulación es un controlador adaptativo por modelo de referencia (MRAC, por sus siglas en inglés) con ley de control por realimentación completa del vector de estado y ajuste en línea de los coeficientes. El desconocimiento de los parámetros del sistema, dígase coeficiente de fricción (B), momento de inercia (J), masa (m) y la localización del centro de masa (l) fundamenta el empleo del controlador mencionado y su estructura general se muestra en la Fig. 5.

Figura 5 Esquema general del controlador adaptativo. 

Al aplicar el procedimiento desarrollado en ^[9] se obtiene que el sistema en lazo cerrado es de segundo orden en ambas articulaciones, por lo que se plantea como único modelo de referencia el siguiente:

(16)

La dinámica deseada en ambos planos es idéntica, y queda definida por los índices de desempeños recogidos en la tabla 1.

Tabla 1 Parámetros de respuesta transitoria. 

No	Índice de desempeño	Magnitud	Unidad
1	Sobre impulso máximo (Mp)	10	%
2	Tiempo de crecimiento (tr)	1	s
3	Tiempo de establecimiento (ts)	3	s
4	Tiempo pico (tp)	1.5	s

El método de cálculo que se emplea es el de respuesta transitoria para sistemas de segundo orden por lo que el factor de amortiguamiento (ξ) es calculado con la ecuación (17).

(17)

Se emplea como sobre impulso máximo para el cálculo de ξ la mitad del permisible debido al efecto inercial de las articulaciones lo que resulta en ξ=0.6901.

El cálculo de la frecuencia natural no amortiguada (ωn) se realiza teniendo en cuenta el tiempo de crecimiento establecido por las exigencias de la plataforma por lo que se emplea la ecuación (18) con β=45° por diseño.

(18)

Con la herramienta MATLAB es modelada la dinámica deseada y se ajusta la ganancia de referencia empleando para ello un paso escalón, por tanto b = 10.5998. El modelo de referencia obtenido es:

En la Fig. 6 se observa el comportamiento deseado a partir de las exigencias de la plataforma.

Figura 6 Dinámica deseada para la plataforma en ambos planos. 

La ley de control deseada es la mostrada en la ecuación (19), donde se incluye un elemento de compensación de los parámetros desconocidos (ΘT Φ(x)) a partir de sus estimaciones:

(19)

El vector de parámetros estimados ΘT y el de funciones conocidas Φ(x) se obtienen de la ecuación (11) para la articulación vertical:

(20)

(21)

Y de la ecuación (12) para la horizontal:

(22)

(23)

La estabilidad del sistema en lazo cerrado se garantiza al aplicar el método de Lyapunov para obtener las dinámicas de adaptación ^[9, ¹⁰, ^36], por lo que, se realiza el procedimiento que se encuentra en ^[9]. Las dinámicas adaptativas obtenidas para ambas articulaciones con ganancias de adaptación Γ y errores de trayectoria e_1,2 se presentan en las ecuaciones (24), (25) y (26).

(24)

(25)

(26)

El vector columna 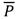perteneciente a la matriz P de la función de Lyapunov que se obtiene es:

Implementación del controlador diseñado

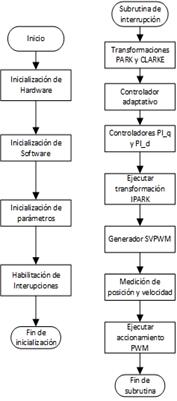
Se propone utilizar un variador de frecuencia de diseño propio, que tiene como procesador el DSP TMS320F28335. En la Fig. 7 es mostrado el diagrama de flujo de la programación realizada en la herramienta Code Composer versión 10, y son empleadas las librerías de control digital de motores de Texas Instruments versión 4.9 para los controladores PI, las transformaciones Clarke, Park, inversa de Park y el generador del vector de tensiones. Con la herramienta MATLAB se genera el código C para el modelo de referencia, leyes adaptativas y cómputo del torque demandado.

Figura 7 Diagrama de flujo de la implementación. 

El motor empleado es el HF-SP152 de Mitsubishi al que se le acopla en el eje un encoder absoluto de 16 bit multivuelta con interfaz CANOpen del fabricante FRABA modelo OCD-CAA1B-1416-S06S-CRW.

Resultados

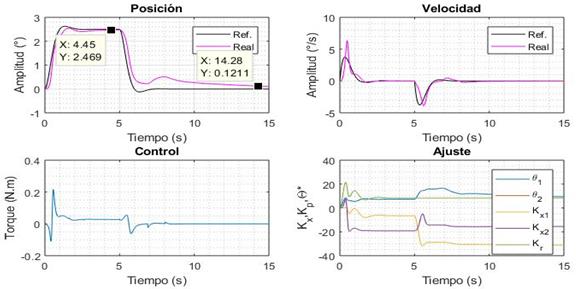
El carácter adaptativo del controlador en la articulación vertical se evalúa al establecer una referencia de 2.5 ° y 5 s después regresa a la posición inicial. Los primeros resultados (Fig. 8) exhiben un sistema estable a lazo cerrado. Los parámetros del controlador muestran un comportamiento deseado ya que en las etapas transitorias sus valores cambian para ajustar la dinámica del sistema.

Los resultados (Fig. 9) después de cuatro ejecuciones muestran que los parámetros del controlador presentan ligeras variaciones en las etapas transitorias y se aparecía un seguimiento de trayectoria fiel lo que evidencia el carácter adaptativo. El tiempo de crecimiento es de 0.99 s y el sobre impulso máximo es de 4 %.

Figura 8 Primeros resultados de la articulación vertical. 

Figura 9 Resultados finales en la articulación vertical. 

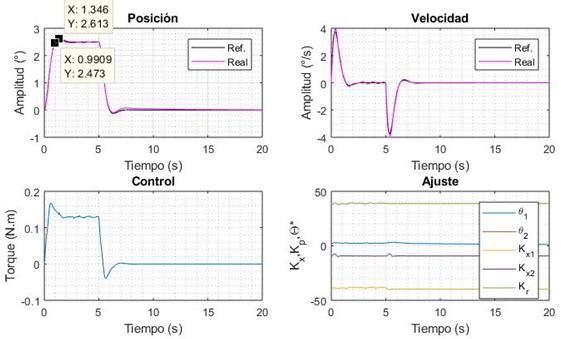
Para evaluar el comportamiento del nuevo controlador frente al original se aplica el estímulo paso escalón con amplitud 10 ° y posición inicial 0 °. Los resultados se recogen en la tabla 2 donde se comparan ambos sistemas apreciándose una mayor precisión con el nuevo controlador al reducirse el error dinámico en 21.38 '.

Tabla 2 Valores comparativos de los índices de desempeño en eslabón vertical. 

	Tiempo de crecimiento (s)	Sobre impulso máximo (%)	Tiempo de establecimiento (s)	Error estático (')	Error dinámico (')
Controlador original	1.5	8.7	3.1	5.4	26.3
Controlador nuevo	0.99	4.9	2.67	1.14	4.92

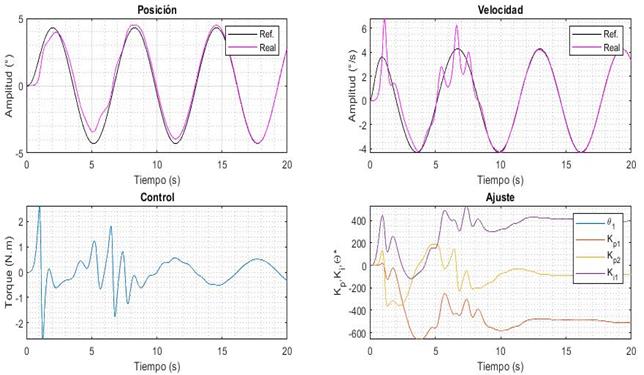
La evaluación del carácter adaptativo en el plano horizontal se realiza con una referencia sinusoidal con amplitud 4.3 ° lo que garantiza en el brazo robótico el régimen de operación sectorial. Los primeros resultados (Fig. 10) muestran una etapa inicial (t < 10.5 s) en la que los parámetros del controlador presentan cambios sustanciales partiendo de 0.

En la segunda etapa (t > 10.5 s) es evidente el cumplimiento de la adaptación al observarse un seguimiento de trayectoria fiel. El comportamiento de los coeficientes del controlador y los parámetros desconocidos del sistema presentan una tendencia a valores constantes.

Figura 10 Resultados de la articulación horizontal. 

Para la evaluación del nuevo controlador frente al original en el plano horizontal, se compara el error dinámico colocando posición inicial 0 ° y aplicar un paso escalón con amplitud 10 °. En la tabla 3 se recogen los resultados de ejecutar el procedimiento mencionado a ambos sistemas apreciándose el incremento de la precisión al reducirse en 17.05 ' el error dinámico.

Tabla 3 Valores comparativos de los índices de desempeño en eslabón horizontal. 

	Tiempo de crecimiento (s)	Sobre impulso máximo (%)	Tiempo de establecimiento (s)	Error estático (')	Error dinámico (')
Controlador original	1.5	9.4	2.9	9	27.1
Controlador nuevo	1.01	4.67	2.62	0.813	10.05

Conclusiones

En el presente trabajo se diseñó un controlador adaptativo por modelo de referencia en conjunto con el control vectorial de motor síncrono de imanes permanentes que garantiza la estabilidad del sistema en lazo cerrado. En los índices de desempeño los valores alcanzados demuestran que el controlador desarrollado mejora la dinámica del brazo robótico.

Se logró la implementación del nuevo controlador en el procesador TMS320F28335, montado en un variador de frecuencia de diseño propio, lo que posibilitó la realización de pruebas experimentales.

Se obtuvo el modelo dinámico del manipulador con la aplicación del método Euler-Lagrange que posibilitó el análisis y diseño de la estrategia de control. Además, permitirá el estudio y análisis del espacio de trabajo y posibles diseños mecánicos para cambios estructurales.

Referencias

1.  Urrea C, Kern J, Álvarez E. Design and implementation of fault-tolerant control strategies for a real underactuated manipulator robot. Complex & Intelligent Systems. 2022;8(6):5101-23.

2.  Rocco P. Stability of PID control for industrial robot arms. IEEE transactions on robotics and automation. 1996;12(4):606-14.

3.  Wazzan AN, Basil N, Raad M, Mohammed HK. PID controller with robotic arm using optimization algorithm. Int J Mech Eng. 2022;7(2):3746-51.

4.  Ibarra-Bonilla MN, Reyes-Castillo I, Sánchez-Texis F. Control de visión inteligente por lógica difusa y RNA para el segui-miento de un objeto aplicado a una estructura robótica de 6 GDL. Revista Ingeniantes. 2018;5(1):1.

5.  Tavoosi J, Mohammadi F, editors. A new type-II fuzzy system for flexible-joint robot arm control. 2019 6th International Conference on Control, Instrumentation and Automation (ICCIA); 2019: IEEE.

6.  Ravandi AK, Khanmirza E, Daneshjou K. Hybrid force/position control of robotic arms manipulating in uncertain environments based on adaptive fuzzy sliding mode control. Applied Soft Computing. 2018;70:864-74.

7.  Suarez Rivera G, Muñoz Ceballos ND, Vásquez Carvajal M. Development of an adaptive trajectory tracking control of wheeled mobile robot. Revista Facultad de Ingenería [Internet]. 2021; 30(55).

8.  Na J, Chen Q, Ren X. Adaptive identification and control of sncertain systems with non-smooth dynamics. ZHU QM, editor. United Kingdom: Academic Press; 2018.

9.  Nguyen NT. Model reference adaptive control. A premier. United States of America: Springer Nature; 2018.

10.  Astrom KJ, Wittenmark B. Adaptive control 2a ed. United States of America: Dover Publications, Inc. ; 2008.

11.  Gu EYL. Advanced dynamics modeling, duality and control robotic systems. 1a ed. 6000 Broken Sound Parkway NW, Suite 300, Boca Raton, FL 33487-2742: CRC Press; 2022.

12.  Spong MW, Hutchinson S, Vidyasagar M. Robot modeling and control. 2a ed. United Kingdom: John Wiley & Sons, Ltd; 2020.

13.  Amna Hasan, Hakeem A. Othman, Altoum SH. q-Euler Lagrange equation. American Journal of Applied Sciences. 2019.

14.  Ramírez GL, García MJ, Siordia VX, García RR. Método de Euler-Lagrange en el modelado y control de un péndulo invertido sobre un carro. Revista de Ingeniería. 2017;1(3):1-8.

15.  Cardoso E, Fernández A, Osorio SAM, Guardado PF. Modelos cinemático y dinámico de un robot de cuatro grados de libertad. Revista de Ingeniería Electrónica, Automática y Comunicaciones. 2017:55-75.

16.  Franco LAM. Diseño de un controlador LQR para un péndulo invertido sobre un carro modelado por el método de Euler-Lagrange. 2020.

17.  Rahmani M, Redkar S. Robot manipulator control using a robust data-driven method. Fractal and Fractional. 2023;7(9):692.

18.  Rodrıguez-Sánchez F, López-Estrada F, Gómez-Penate S, Valencia-Palomo G, Dominguez-Zenteno J. Modelo Dinámico Convexo de una Grúa Mecánica con 3 Grados de Libertad. Jornada de Ciencia y Tecnología Aplicada. 2021;4(1).

19.  Serrano FE, Rodriguez BA, Cardona M. Obtención de un modelo dinámico para un robot 3RRR basado en teoría de screws. Revista Iberoamericana de Automática e Informática Industrial. 2018;15(4):384-90.

20.  Borja MB. Sistema de posicionamiento con visión artificial para un brazo robótico articulado de seis grados mediante redes neruonales artificiales. 16th LACCEI International Multi-Conference for Engineering, Education, and Technology: “Innovation in Education and Inclusion”. 2018.

21.  Mijares JS, Fraire LJF, De La Torre REC, Juárez AR. Control de brazo robótico de tres grados de libertad con de procesamiento digital de imágenes para seguimiento de un brazo humano. Pistas Educativas. 2019;41(134).

22.  Morones-Reyes J, Guerrero-Castellanos J, Soto-García E, Linares-Flores J, la Mixteca HdL. Control de posición de miembros superiores de un robot antropomórfico: una fusión de CLF y observadores de EE. 2019.

23.  Yilmaz E, Zaki H, Unel M, editors. Nonlinear adaptive control of an aerial manipulation system. 2019 18th European control conference (ECC); 2019; Naples, Italy: IEEE.

24.  López-Hoyos JC, Cervantes-Rojas JS, Ordaz-Oliver P. Control adaptable para un vehículo aéreo no tripulado ante cambios de carga útil con aplicaciones en agricultura de precisión. Pädi Boletín Científico de Ciencias Básicas e Ingenierías del ICBI. 2022;9(18):92-9.

25.  Marquina MJB, Jose CJFR, Sandoval AHM, Escobedo AOT, Alcántara JHA. Identificación no paramétrica de un brazo robótico de 2 GDL utilizando redes neuronales RBF. Revista de Investigaciones. 2021;10(4):370-8.

26.  Fernández REC, Marca MFM. Diseño de un control neuronal aplicado a un brazo robótico de alta precisión. Sapienza: International Journal of Interdisciplinary Studies. 2022;3(2):442-52.

27.  Linares Barranco A, Jiménez Fernández ÁF, Jiménez Moreno G, Gutiérrez Galán D, Ríos Navarro JA. Control neuromórfico del brazo robótico BIOROB del Citec de la Universidad de Bielefeld. V jornada de investigación y postgrado de la Escuela Politécnica Superior de Sevilla (2019), p 125-138. 2019.

28.  Garzón A, Angulo M, Domínguez A. Control difuso de un motor de inducción. Ingeniería Energética. 2005:pp. 32-6.

29.  Caponio A, Cascella GL, Neri F, Salvatore N, Sumner M. A fast adaptive memetic algorithm for online and offline control design of PMSM drives. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics). 2007;37(1):28-41.

30.  Cuji W, Arcos-Aviles D. Control directo al par y control de campo orientado para un motor síncrono de imanes permanentes. Revista Ingeniería. 2019;24(2):143-58.

31.  Mejias OA, Olivera RT, Cambero IR, Popocatl HM. Controlador de velocidad adaptativo para un motor Síncrono de Imanes Permanentes. Nova Scientia. 2019;11(22):142-70.

32.  Hughes A, Drury B. Electrics motors and drives. Fundamentals, types and applications. 5a ed. Estados Unidos: Joe Hayton; 2019.

33.  Nam KH. AC motros control and electrical vehicle applications. 2a ed. New York: CRC Press; 2019.

34.  Kim S-H. Current regulators of alternating current motors. Electric motor montrol DC, AC, and BLDC motors. Netherlands: Elsevier; 2017.

35.  Wang L, Chai S, Yoo D, Gan L, Ng K. PI current and voltage controller design for power converter. PID and predictive control of electrical drives and power converters using MATLAB/Simuink. Singapore: IEEE Press; 2015.

36.  Qi R, Tao G, Jiang B. Adaptive control: A tutorial introduction. Fuzzy system identification and adaptive control. Switzerland Springer Nature Switzerland AG; 2019.

Recibido: 01 de Febrero de 2024; Aprobado: 01 de Junio de 2024

^* Autor para la correspondencia: [e-mail]

No existen conflictos de intereses entre los autores, ni de la institución en relación al contenido del artículo aquí reflejado.

Yordany Vélez Rodríguez: Conceptualización, Investigación, Análisis Formal, Software, Metodología, Validación-Verificación y Redacción-borrador original.

Jorge H. Vázquez Leiva: Conceptualización, Investigación, Análisis Formal, Redacción- borrador original.

José E. Vargas Fernández: Curación de dato, Análisis formal y Validación -Verificación.

Yordany Vélez Rodríguez, Ingeniero Radioelectrónico en la especialidad de Aviación, Aspirante a Investigador, labora en el Centro de Investigación y Desarrollo de la Electrónica, Mecánica y Automática “CID MECATRONICS”, La Habana, Cuba. Correo electrónico [e-mail]. No. ORCID: 0000-0003-2675-3476.

Jorge H. Vázquez Leyva, Ingeniero en Telecomunicaciones, Aspirante a Investigador, labora en el Centro de Investigación y Desarrollo de la Electrónica, Mecánica y Automática “CID MECATRONICS”, La Habana, Cuba. Correo electrónico [e-mail]. No. ORCID: 0000-0002-7201-5514.

José E. Vargas Fernández, Ingeniero en Telecomunicaciones, Investigador Agregado, labora en el Centro de Investigación y Desarrollo de la Electrónica, Mecánica y Automática “CID MECATRONICS”, La Habana, Cuba. Correo electrónico [e-mail]. No. ORCID: 0000-0003-4897-1618.