Introducción
Los avances tecnológicos han incorporado nuevas plataformas de comunicación directa, sincrónica o asincrónica, que ayudan a transformar la enseñanza y el aprendizaje al hacer posible que los estudiantes se responsabilizan de su propio aprendizaje y cooperan con otros de manera significativa.
Las plataformas facilitan la adquisición de información, el trabajo compartido y la participación en el ámbito educativo permite crear estrategias de enseñanza (Quevedo et al., 2022) como resultado del auge de las Tecnologías de Información y Comunicación (Tic) que ha supuesto una transformación radical en la forma de crear, conservar, difundir y acceder a la información (Cueva et al., 2019).
Las Ticson herramientas que facilitan y enriquecen el actual proceso de enseñanza aprendizaje, al permitir adquirir información, recursos y servicios educativos, así como crear y compartir contenidos propios.
Asimismo, favorecen el desarrollo de competencias digitales, la colaboración, la creatividad (Islas, 2021), el pensamiento crítico, la autonomía (Maliza et al., 2021) y ofrecen nuevas posibilidades de personalización, adaptación, evaluación del aprendizaje, de interacción y comunicación entre docentes, estudiantes y familias (Cueva et al., 2019).
En las plataformas virtuales, las aulas contienen los objetivos de la planificación y el programa de la asignatura; pero además exigen del docente demostrar capacidad en el desarrollo del contenido de una manera creativa e innovadora (Plaza et al., 2021). De esta manera, la función del docente consiste en crear un ambiente de aprendizaje donde los estudiantes puedan interactuar entre sí y con los materiales del curso de manera significativa (Guevara et al., 2021).
El docente en el aula virtualdeberá diseñar actividades que promuevan la interacción, el trabajo en equipo, la ayuda, la creatividad y el pensamiento crítico. Además, debe brindar retroalimentación oportuna y personalizada, así como evaluar los avances las necesidades emocionales, sociales de los estudiantes y fomentar un clima de confianza y respeto.
En ese sentido, la educación virtual es considerada en una modalidad cada vez más extendida y demandada en el actual contexto, principalmente como consecuencia de la pandemia de COVID-19, dadas las exigencias, experiencias y aprendizajes que ella impuso para la educación; así como la flexibilización e inclusión educativa que con ella se logró (Pinos et al., 2020).
La enseñanza virtual se caracteriza por la flexibilidad horaria y espacial; la personalización del aprendizaje, el desarrollo de la autonomía, la responsabilidad, el uso de recursos tecnológicos variados y motivadores, así como la posibilidad de interactuar con otros estudiantes y docentes a través de plataformas digitales (Plaza et al., 2022).
A su utilización se le asocian herramientas de comunicación (chats, foros, videoconferencias), de creación de contenido (presentaciones, vídeos, animaciones, simulaciones, juegos) y de gestión del aprendizaje (portafolios electrónicos, sistemas de seguimiento y análisis del rendimiento).
Sin embargo, se le atribuyen limitaciones cuando su uso está asociado a: falta de acceso a Internet o a dispositivos adecuados, dificultad para mantener la atención y la concentración, la existencia de escasa retroalimentación y evaluación, el aislamiento social y emocional que la acompañan y la necesidad de contar con docentes capacitados y actualizados en el uso de las herramientas virtuales (Torres et al., 2022). La labor del docente se dificulta más aún en el intento por vincular la enseñanza de la matemática a las herramientas tecnológicas que ofrecen las plataformas digitales.
En consecuencia, las tendencias educativas actuales denotan que el desarrollo tecnológico ha generado la urgencia de adoptar metodologías dinámicas y efectivas que fomenten la participación activa y el compromiso de los estudiantes. En este contexto, la plataforma Moodle irrumpe como una herramienta competente que permite la implementación de estas estrategias didácticas, innovadoras, accesibles para la enseñanza y en especial de las matemáticas
En Ecuador, las bases fundamentales de la educación inclusiva e investigativa pedagógica apoyan la enseñanza virtual de las matemáticas mediante diversos programas educativos, como el Programa Nacional de Educación a Distancia y Virtual, el Proyecto Educativo Matemático (PEM), el Programa de Formación Docente en Matemática, y el Sistema Nacional de Evaluación Educativa, respaldados por la Constitución de la República del Ecuador.
Recientes investigaciones muestran resultados positivos para contribuir con el aprendizaje y dominio de determinadas habilidades matemáticas, para la enseñanza de la correlación (Pérez et al., 2023), mientras que Usiña (2023) demuestra como los recursos didácticos interactivos en Moodle favorecen el uso de estrategias de aprendizaje y la motivación de los estudiantes. Balladares et al. (2020) los utiliza para diseñar actividades lúdicas, variadas y contextualizadas, fomentar la comunicación sincrónica y asincrónica y fortalecer los conocimientos básicos y el razonamiento lógico-matemático de los estudiantes.
Sin embargo, en otras investigaciones se reflejan limitaciones en su introducción, por ejemplo, Collantes et al. (2022) las establece para cuando está asociada a la falta de: competencias tecnológicas de los docentes, conectividad o de equipos tecnológicos en las instituciones educativas, motivación e interés por la asignatura o la escasa interacción entre los participantes.
La enseñanza de las matemáticas en el primer año de Bachillerato requiere la comprensión y asimilación de conceptos complejos que demandan estrategias pedagógicas innovadoras, donde se resalta la necesidad de adaptar métodos de enseñanza que fomenten la comprensión profunda de los contenidos matemáticos (Darling et al., 2020).
La presente investigación se propone abordar la problemática en la enseñanza de las matemáticas para el primero de Bachillerato, específicamente la enseñanza del sistema de ecuaciones con dos incógnitas, con su integración a la plataforma Moodle como apoyo didáctico para mejorar el proceso de enseñanza y aprendizaje en esta disciplina.
La enseñanza de las matemáticas en la Unidad Educativa Réplica Nicolás Infante Díaz se caracteriza porque los docentes reconocen que no poseen todos los recursos necesarios, no se utiliza el debate en las clases, se utiliza fundamentalmente la enseñanza tradicional y se reconoce la falta de confianza de los estudiantes para enfrentar el aprendizaje de este contenido. Por otra parte, se pudo constatar que las calificaciones de los estudiantes son bajas y la tendencia de las notas decrece respecto a años anteriores, existen deficiencias en las planificaciones curriculares, limitado uso de herramientas digitales y limitada participación de los estudiantes en las clases.
Por estas razones, se propone desarrollar una estrategia de enseñanza, apoyada en la virtualidad, para enseñar sistemas de ecuaciones lineales con dos incógnitas a estudiantes de primero de bachillerato en la asignatura de Matemáticas de la Unidad Educativa Réplica Nicolás Infante Díaz de la ciudad de Quevedo.
Materiales y métodos
Se aplicó un enfoque en la investigación cuantitativo, que se apoya en la objetividad y la búsqueda de generalizaciones para comprender los fenómenos a través de la inferencia. La investigación es de tipo transversal por implementarse para un período de tiempo determinado, correlacional por vincular la implementación de una estrategia con apoyo de la plataforma Moodle y con percepción de los estudiantes de obtener mejores resultados en el aprendizaje de las matemáticas; con alcance aplicado para los estudiantes de primero de bachillerato en la asignatura de Matemáticas de la Unidad Educativa Réplica Nicolás Infante Díaz de la ciudad de Quevedo.
Se utilizaron métodos teóricos que incluyeron el análisis - síntesis, inducción - deducción, enfoque en sistema e histórico lógico en el estudio y sistematización del marco teórico conceptual necesario (Quesada y Medina, 2020); empíricos, como: observación, revisión documental, entrevistas y cuestionarios en el diagnóstico necesario para la construcción de la estrategia y estadísticos descriptivos para el análisis de los resultados.
La recolección de información, se aplica al total de la población, constituida por dos docentes y 55 estudiantes de dos paralelos. A los docentes se les realiza una entrevista y a los estudiantes se les aplica un cuestionario que consta de dieciocho preguntas cerradas donde el docente debe responder afirmativamente (sí) o negativamente (no) sobre la utilización de diferentes estrategias en la enseñanza de ecuaciones lineales de primer grado.
Posterior a la implementación de la estrategia, se les administra un segundo cuestionario a los estudiantes para determinar los cambios experimentados por la estrategia con el apoyo de la plataforma digital Moodle que constó de cinco preguntas cerradas donde el estudiante debe responder afirmativamente (sí) o negativamente (no) acerca de su precepción de la efectividad de las estrategias de enseñanza empleadas.
Para la validación del contenido de los instrumentos se asocia que si toma el valor de 2 y no el valor de 1 y se procede a aplicar el coeficiente de validez de contenido (Cvc) sugerido por Hernández-Nieto abordado por Sánchez (2021) que valora el grado de acuerdo por ítems entre los jueces o evaluadores. Los resultados obtenidos para los tres cuestionarios aplicados resultaron de 0.9758, 0.9747 y 0.9725 respectivamente, todos superiores a 0.90 límite establecido para considera que existe concordancia entre los planteamientos de los encuestados.
Por último, se seleccionan 10 docentes de la institución, incluye directivos, caracterizados por su experiencia docente y se les solicita que evalúen según el Índice de Promotores Neto a la estrategia creada lo que permite evaluar la capacidad de recomendación de la propuesta realizada por los docentes implicados (García, 2018).
Resultados y discusión
Propuesta simplificada de la estrategia
La propuesta contempla el diseño de una estrategia didáctica sustentada en la virtualidad para enseñar sistemas de ecuaciones lineales con dos incógnitas dirigidas a los estudiantes de primero de bachillerato en la asignatura de Matemáticas de la Unidad Educativa Réplica Nicolás Infante Díaz de la ciudad de Quevedo. Su concesión, de forma resumida, se realiza en aproximación a Collantes et al. (2022); Medina (2011) y es la siguiente:
Título de la estrategia
Sistema de ecuaciones lineales con dos incógnitas sustentadas en la virtualidad
Introducción
El diseño de una estrategia didáctica adaptada al contexto de estudiantes de matemáticas de primero de Bachillerato se fundamenta en la premisa de proporcionar un enfoque pedagógico innovador y personalizado (Henry, 2020), con sustento en las funcionalidades de Moodle para desarrollar actividades interactivas, recursos multimedia y evaluaciones formativas que estimulen habilidades cognitivas superiores y aplicar conceptos matemáticos a situaciones de la vida real (Bueno et al., 2020).
En la propuesta, se pretende desarrollar habilidades cognitivas, tales como, como pensar lógica y críticamente, analizar problemas e identificar soluciones, razonar deductivamente e inductivamente, hacer inferencias, sacar conclusiones y utilizar el pensamiento abstracto (Österman y Bråting, 2019).
Para el desarrollo de habilidades lógicas, las matemáticas enseñan cómo identificar patrones y relaciones, hacer generalizaciones, formular y probar hipótesis, construir pruebas y argumentos y evaluar evidencia.
En el área creativa, se busca que los estudiantes logren pensar de manera lateral, proponer a los problemas soluciones nuevas e innovadoras y usar su imaginación para explorar conceptos.
El sistema de ecuaciones con dos incógnitas es indispensable para el perfeccionamiento del pensamiento algebraico y la resolución de problemas matemáticos. Sin embargo, su enseñanza suele presentar dificultades tanto para los docentes como para los estudiantes, debido a la complejidad de los conceptos involucrados y a las limitaciones de los métodos tradicionales (Bueno et al., 2020).
Objetivo general
Desarrollar una estrategia didáctica con apoyo Moodle para la enseñanza de problemas de sistema de ecuaciones con dos incógnitas en primero de bachillerato en la Unidad Educativa Réplica Nicolás Infante Díaz, de la ciudad de Quevedo.
Objetivos Específicos
Conocer las estrategias empleadas en la enseñanza de problemas de ecuaciones lineales con dos incógnitas de los estudiantes de primero.
Diseñar una estrategia didáctica acerca de la enseñanza de problemas de ecuaciones lineales con dos incógnitas para los estudiantes de primero de bachillerato de la Unidad Educativa Replica Nicolás Infante Díaz con el uso de la plataforma Moodle.
Aplicar la estrategia didáctica sobre la enseñanza de problemas, a través de la plataforma Moodle.
Público objetivo
Estudiantes de primero de bachillerato de la Unidad Educativa Replica Nicolás Infante Díaz.
Responsable de la concreción de la estrategia
Profesores de matemática de primero de bachillerato de la Unidad Educativa Replica Nicolás Infante Díaz.
Fundamentación teórica
La propuesta de actividades pedagógicas para la enseñanza de ecuaciones lineales con dos incógnitas surge como respuesta a la constante búsqueda de metodologías innovadoras y efectivas en la enseñanza.
Actualmente, se reconoce la importancia de desarrollar estrategias didácticas que no solo faciliten la comprensión de conceptos abstractos, como las ecuaciones lineales, sino que además promuevan la participación activa, la aplicación práctica y la construcción de significado en los estudiantes.
La necesidad de esta propuesta se fundamenta en la complejidad que enfrentan los estudiantes al abordar conceptos matemáticos como las ecuaciones lineales con dos incógnitas. Este tema suele ser desafiante debido a su abstracción y a la falta de conexiones con la realidad cotidiana de los estudiantes. Asimismo, se evidencia la necesidad de superar el enfoque tradicional de enseñanza, que a menudo se centra en memorizar fórmulas y procedimientos sin una comprensión profunda de los conceptos.
En este contexto, la propuesta de la estrategia se erige como una herramienta clave para transformar la dinámica de aprendizaje, con un enfoque pedagógico activo, participativo y contextualizado. Esta propuesta busca facilitar la comprensión de las ecuaciones lineales y también fomentar la aplicación práctica de los conceptos y promover un aprendizaje significativo que perdure más allá del aula y permita a los estudiantes desarrollar habilidades matemáticas sólidas y pertinentes en su vida cotidiana.
La estrategia se alinea con la teoría constructivista al promover la construcción activa del conocimiento y se caracteriza porque los estudiantes participan en la resolución de problemas, debates y creación de situaciones contextualizadas, lo que fomenta la construcción de significados y la comprensión profunda de las ecuaciones lineales.
Por otro lado, al involucrar a los estudiantes en el vínculo de los estudiantes a situaciones reales o factibles, se busca que relacionen los conceptos abstractos de las ecuaciones lineales con situaciones reales, que faciliten un aprendizaje más significativo y aplicable.
Asimismo, la estrategia se alinea con la teoría aprender haciendo al involucrar a los estudiantes en actividades prácticas que promueven la resolución de problemas y la aplicación de conceptos a la vida cotidiana, fomentando un aprendizaje activo y significativo.
Para ejecutar las actividades planteadas, el docente debe:
Facilitar el acceso a la plataforma Moodle y proporcionar las indicaciones y recursos necesarios para cada actividad.
Monitorear y moderar las discusiones y debates en los foros, brindando orientación cuando sea necesario.
Fomentar un ambiente de trabajo colaborativo y participativo en los grupos.
Ofrecer directrices claras sobre la creación de problemas contextualizados.
Establecer criterios de autoevaluación y revisión entre pares para garantizar la calidad de la retroalimentación.
El docente desempeña un papel fundamental como facilitador del aprendizaje, al guiar y apoyar a los estudiantes en cada etapa de la propuesta, incentivando la participación, el pensamiento crítico y la construcción activa del conocimiento en el contexto de las ecuaciones lineales.
Importancia de la Propuesta
Garantiza accesibilidad y flexibilidad, ya que Moodle permite el acceso a recursos y actividades en cualquier momento y lugar, promoviendo la continuidad del aprendizaje más allá del aula. Los estudiantes pueden acceder a materiales y participar en actividades según su propio ritmo y horario, promoviendo así la flexibilidad en el proceso de aprendizaje.
También, la plataforma Moodle ofrece herramientas para adaptar la enseñanza a las necesidades individuales de los estudiantes. Se pueden crear actividades diferenciadas, ofrecer recursos adicionales según el nivel de comprensión de cada estudiante y proporcionar retroalimentación personalizada, lo que fomenta un aprendizaje más personalizado y efectivo.
De igual manera, la integración de Moodle permite crear actividades y recursos que conectan los conceptos abstractos de las ecuaciones lineales con situaciones de la vida real. Mediante casos prácticos, problemas contextualizados y ejemplos relevantes, se refuerza la comprensión de la utilidad y aplicabilidad de las ecuaciones lineales en diferentes contextos, generando así un aprendizaje más significativo.
Asimismo, Moodle ofrece diversas herramientas para la interacción entre estudiantes y con el docente, como foros de discusión, actividades grupales y espacios de interacción en tiempo real. Esto fomenta el intercambio de ideas, el debate y la colaboración entre estudiantes, promoviendo un aprendizaje más activo y social.
Finalmente, la plataforma Moodle permite la creación de actividades evaluativas que permiten la retroalimentación inmediata. Los estudiantes reciben información sobre su desempeño de manera continua, lo que les ayuda a identificar áreas de mejora y a reforzar su comprensión de las ecuaciones lineales de manera progresiva.
Resultados del estudio diagnóstico
Resultados del cuestionario para los docentes
Se exponen las tablas 1, 2, 3, 4, 5 y 6 asociada a las respuestas de los docentes de matemáticas acerca de: selección y presentación de contenidos matemáticos;la utilización de los recursos de los docentes para la enseñanza de este contenido; la metodología de enseñanza empleada para abordar la enseñanza de las ecuaciones con dos incógnitas; vías para la concreción de la estrategia y su utilización en la actualidad; fomento del pensamiento crítico y desarrollo de habilidades matemáticas respectivamente. Cada tabla se acompaña de su interpretación.
Tabla 1 - Selección y presentación de contenidos matemáticos, según los docentes.
| Pregunta | Sí | No |
|---|---|---|
| ¿Abarca usted la amplitud del tema de ecuaciones lineales con dos incógnitas en su plan de enseñanza? | 2 | |
| ¿Logra abordar con detalle y complejidad el tema de las ecuaciones lineales con dos incógnitas en su enseñanza? | 2 | |
| ¿Puede planificar y ejecutar la secuencia lógica de enseñanza para garantizar una progresión adecuada en el aprendizaje de ecuaciones lineales con dos incógnitas? | 2 |
Fuente: elaboración propia.
Los docentes encuestados afirmaron que abordan la amplitud del temario con un nivel de profundidad de la enseñanza completo en un orden y coherencia adecuados para la enseñanza de las ecuaciones lineales con dos incógnitas.
Tabla 2 - Utilización de recursos didácticos.
| Pregunta | Sí | No |
|---|---|---|
| ¿Cuenta con una variedad de recursos y materiales para ofrecer una enseñanza variada y enriquecedora en el tema de ecuaciones lineales de dos incógnitas? | 2 | |
| ¿Considera usted que las estrategias de enseñanza estén alineadas con los objetivos específicos de aprendizaje en ecuaciones lineales de dos incógnitas? | 2 | |
| ¿Cree usted que los métodos o herramientas que emplea durante la enseñanza de ecuaciones lineales fomentan la interacción y participación activa de los estudiantes? | 2 |
Fuente: elaboración propia.
Se muestra que los docentes no cuentan con todos los recursos o materiales necesarios para ofrecer una enseñanza variada del tema, sin embargo, a pesar, consideran que sus estrategias y métodos de enseñanza cumplen con los objetivos específicos y fomentan la interacción y participación activa de los estudiantes.
Tabla 3 - Metodología de enseñanza.
| Pregunta | Sí | No |
|---|---|---|
|
¿Considera que el siguiente enfoque pedagógico es efectivo al enseñar ecuaciones lineales de primer grado? Tradicional Constructivista Basado en competencias Otro (indique): |
2 | |
| ¿Promueve la participación activa de los estudiantes durante las clases de ecuaciones lineales con dos incógnitas mediante este enfoque? | 2 | |
| ¿Este enfoque le permite adaptar su metodología para atender los diferentes estilos de aprendizaje presentes en su aula? | 2 |
Fuente: elaboración propia.
Ambos docentes reconocen que emplean fundamentalmente el enfoque pedagógico tradicional y solo elementos aislados del enfoque constructivista. Ambos consideran que estos enfoques les ayudan a promover una participación activa y adaptada a los estilos de aprendizaje.
Tabla 4 - Estrategias para resolver problemas.
| Pregunta | Sí | No |
|
¿Usa ejemplos y ejercicios prácticos para desarrollar habilidades de resolución de problemas de las ecuaciones lineales con dos incógnitas durante sus clases? |
2 | |
|
¿Estimula la búsqueda de diferentes formas de abordar problemas durante sus clases? |
2 | |
|
¿Ofrece retroalimentación a los estudiantes durante la enseñanza de ecuaciones lineales? |
2 |
Fuente: Elaboración propia.
Los docentes afirman emplear ejemplos, ejercicios prácticos, la retroalimentación para abordar problemas de ecuaciones lineales con dos incógnitas y desarrollar en ellos habilidades de resolución de problemas, donde el estudiante aprende a buscar diferentes formas o métodos para resolver problemas de ecuaciones lineales con dos incógnitas. Estas habilidades guardan relación con el pensamiento crítico y el desarrollo general de habilidades matemáticas.
Tabla 5 - Fomento del pensamiento crítico.
| Pregunta | Sí | No |
| ¿Usa preguntas abiertas que estimulen la reflexión y el análisis en los estudiantes durante la enseñanza de ecuaciones lineales? | 1 | 1 |
| ¿Fomenta el debate y la argumentación entre los estudiantes al abordar ecuaciones lineales? | 2 | |
| ¿Evalúa de forma crítica el progreso y comprensión de los estudiantes en el tema de ecuaciones lineales? | 2 |
Fuente: elaboración propia.
Un docente emplea preguntas abiertas para estimular la reflexión y el análisis durante sus clases, el otro docente no. Con respecto al debate y la argumentación, los docentes reconocen fomentar el pensamiento crítico en el proceso de evaluación.
Tabla 6 - Desarrollo de habilidades matemáticas.
| Pregunta | Sí | No |
| ¿Evalúa usted el desempeño de los estudiantes en evaluaciones relacionadas con ecuaciones lineales? | 2 | |
| ¿Evalúa usted la capacidad de los estudiantes para aplicar conceptos de ecuaciones lineales a situaciones del mundo real? | 2 | |
| ¿Considera usted que sus estudiantes demuestran seguridad y confianza al abordar problemas de ecuaciones lineales? | 2 |
Fuente: elaboración propia.
Para medir el desempeño de los estudiantes en las ecuaciones lineales con dos incógnitas por parte de ambos docentes se basan en la realización de evaluaciones. Estas, contemplan la resolución de problemas y la aplicación los conceptos del tema a situaciones reales. Consideran que los estudiantes no demuestran seguridad y confianza al abordar problemas de ecuaciones lineales con dos incógnitas.
Resultados de la observación y la revisión documental
En la revisión documental asociada a los docentes de matemática y que contempla: los informes de visitas áulicas, el Plan Operativo Anual (POA) de actividades programadas, las calificaciones de los estudiantes de bachillerato en la asignatura, las planificaciones micro curriculares, la aplicación de métodos y estrategias correspondientes a las necesidades de los estudiantes; se obtuvo que:
La programación del cronograma anual de actividades del área de Matemática contempla la participación de docentes y estudiantes en el 80 % de las actividades propuestas, con lo que se cumple lo que dispone el Ministerio de Educación (MINEDUC).
Se pudo observar que de la muestra seleccionada; 6 estudiantes dominan los aprendizajes requeridos con un puntaje de 9-10 puntos, 27 obtienen los puntajes requeridos entre 7-8.99 puntos y 22 estudiantes están próximos a alcanzar los aprendizajes con un puntaje de 4- 6,99.
Se observan deficiencias en las planificaciones microcurriculares de los docentes en cuanto al planteamiento de métodos y técnicas para el aprendizaje de la asignatura de Matemática; así como el limitado uso de herramientas digitales para un mejor proceso de enseñanza-aprendizaje.
Al revisar las calificaciones en el área de Matemáticas se analiza que en los últimos dos años el promedio de calificaciones posee una tendencia a decrecer.
En la ejecución de la clase se cumple lo planificado, sin embargo, la participación de los estudiantes es muy limitada.
Propuesta de solución al problema
La tabla 7 muestra de forma resumida la estrategia didáctica propuesta con el apoyo de la plataforma Moodle para el tema de sistema de ecuaciones lineales con dos incógnitas dirigidas a los estudiantes de primero de bachillerato en la asignatura de Matemáticas de la Unidad Educativa Réplica Nicolás Infante Díaz de la ciudad de Quevedo.
Tabla 7 - Estrategia didáctica con el apoyo de la plataforma digital Moodle.
| Objetivo 1.1 | Desarrollar habilidades de resolución de problemas | ||
|---|---|---|---|
| Descripción de la actividad | Tiempo | Evaluación | Recursos necesarios |
| Foro de discusión: Publicación de problemas de ecuaciones lineales para que los estudiantes los resuelvan y discutan en el foro, ofreciendo diferentes enfoques y soluciones. | 2 semanas | Participación en el foro, calidad de argumentación y soluciones propuestas. | Plataforma Moodle, foro de discusión. |
| Objetivo 1.2 | Promover el aprendizaje colaborativo | ||
| Trabajo en grupos: Asignación de problemas desafiantes para resolver en grupos, fomentando el debate y la colaboración para llegar a soluciones consensuadas. | 3 sesiones de clase | Presentación oral de las soluciones y coherencia en el trabajo en grupo. | Aula virtual en Moodle, material de apoyo. |
| Objetivo 1.3 | Estimular la creatividad y aplicación práctica | ||
| Creación de problemas contextualizados: Los estudiantes deben crear problemas de ecuaciones lineales con ejemplos de la vida real y compartirlos en un repositorio. | 1 semana | Calidad y originalidad de los problemas planteados. | Herramientas de creación de texto en Moodle. |
| Objetivo 1.4 | Evaluación formativa y retroalimentación | ||
| Autoevaluación y revisión de pares: Los estudiantes resuelven problemas, se autoevalúan y reciben retroalimentación de sus compañeros. | 1 semana | Coherencia en la autoevaluación y retroalimentación brindada. | Rubricas de autoevaluación, espacio para revisión de pares en Moodle. |
Fuente: elaboración propia.
Para monitorear y apoyar efectivamente el proceso de desarrollo de las actividades en Moodle se recomienda:
Establecer una Comunicación mediante instrucciones claras y fáciles de entender. Crear foros de consulta para hacer preguntas y esclarecer dudas y proporcionar un medio adicional de comunicación, como un correo electrónico o una sala de chat, para consultas más directas.
Realizar seguimientos periódicos de los que participan. Utilizar los informes que ofrecen las plataformas. De igual manera, brindar retroalimentación constante durante las actividades.
Fomentar la colaboración mediante grupos de trabajo y foros de discusión.
Ofrecer recursos de apoyo como material complementario, ya sea en persona o a través de video llamadas, para aquellos que necesiten ayuda adicional.
Utilizar herramientas de seguimiento, tales como, el registro de actividades para ver el tiempo dedicado por los estudiantes a cada recurso o actividad; las funcionalidades de calificaciones y retroalimentación de Moodle.
Establecer Expectativas claras a través del calendario y fechas límite para que los estudiantes puedan planificar su trabajo.
Promover la autonomía y la autogestión al permitir que los estudiantes tomen decisiones sobre su aprendizaje y les brinden la responsabilidad de su progreso. También se recomienda ofrecer pautas sobre cómo administrar su tiempo y recursos para completar las actividades.
Al combinar estas estrategias y utilizar las herramientas disponibles en Moodle, el docente podrá monitorear y apoyar de manera efectiva a sus estudiantes en las actividades en línea.
Pasos para plantear problemas desafiantes y alentar la participación activa en discusiones
Contextualización: Introduce el problema proporcionando un contexto relevante. Puedes relacionarlo con situaciones del mundo real que involucren ecuaciones lineales para hacerlo más significativo.
Desafío Matemático: Formula un desafío matemático que implique la aplicación de ecuaciones lineales. Asegúrate de que el problema sea lo suficientemente complejo como para requerir razonamiento y análisis.
Preguntas Reflexivas: Plantea preguntas que fomenten la reflexión y el análisis crítico. Por ejemplo, ¿cómo se relaciona este problema con situaciones cotidianas? ¿Qué estrategias propones para resolverlo?
Estímulo a la Creatividad: Promueve abordar el problema de manera creativa. Pueden proponer diversas formas de resolverlo o incluso plantear variantes del mismo.
Conexiones Interdisciplinarias: Explora conexiones interdisciplinarias, si es posible. ¿Cómo se relaciona este problema con otras áreas de estudio? ¿En qué medida se puede aplicar en diferentes contextos?
Recomendaciones para alentar la participación activa
Establece Normas de Participación: Define expectativas claras sobre la frecuencia y calidad de las contribuciones. Anima a los estudiantes a expresar sus ideas de manera respetuosa y constructiva.
Promueve la Colaboración: Sugiere que los estudiantes colaboren entre ellos para abordar el problema. Pueden compartir enfoques, discutir estrategias y ofrecer retroalimentación.
Fomenta la Diversidad de Enfoques: Valora y celebra la diversidad de enfoques. Anima a los estudiantes a explorar diferentes métodos de resolución y a comparar sus resultados.
Ofrece Retroalimentación Significativa: Proporciona retroalimentación detallada sobre las contribuciones de los estudiantes. Destaca los aspectos positivos y sugiere mejoras o extensiones a sus respuestas.
Reconoce y Premia el Esfuerzo: Reconoce el esfuerzo y la participación constante. Puedes establecer incentivos, como reconocimientos especiales o puntos adicionales, para motivar a los estudiantes.
Pasos para crear y gestionar grupos colaborativos en Moodle
Los grupos permiten que los estudiantes trabajen juntos, compartan ideas y resuelvan problemas en equipo. También, facilitan la adaptación de las actividades y recursos según las necesidades de cada grupo. Los estudiantes pueden sentirse más motivados al trabajar en entornos donde se fomenta la colaboración y la interacción. Los profesores pueden supervisar el progreso de cada grupo y brindar apoyo específico cuando sea necesario. Cabe destacar que la efectividad de los grupos colaborativos depende de la claridad en las instrucciones, el establecimiento de roles claros y la retroalimentación constante para asegurar un ambiente colaborativo y productivo. Se proponen los pasos siguientes:
Paso 1: Accede al curso en Moodle. Ingresa al curso donde deseas crear el grupo y accede al panel de administración del curso.
Paso 2: Accede a la configuración del curso. En el panel de administración, busca la opción Usuarios o Participantes. Aquí encontrarás la sección de Grupos o Grupos de Usuarios.
Paso 3: Crear grupos. Selecciona la opción para crear grupos. Define el nombre del grupo y establece el método de agrupación (puedes optar por agrupación manual o automática).
Paso 4: Añadir participantes a los grupos. Agrega a los estudiantes a cada grupo. Puedes hacerlo manualmente asignando a cada estudiante a un grupo específico o permitir que Moodle realice la distribución automática.
Paso 5: Comunicación y colaboración. Anima a los estudiantes a utilizar las herramientas de comunicación disponibles en Moodle para intercambiar ideas y colaborar en proyectos grupales. Pueden utilizar foros, chats, mensajes, etc.
Paso 6: Actividades y recursos grupales. Asigna tareas, cuestionarios o proyectos específicos a cada grupo. Puedes configurar actividades que solo estén disponibles para determinados grupos.
Paso 7: Seguimiento del progreso. Utiliza las herramientas de seguimiento de Moodle para monitorear el progreso de cada grupo. Puedes revisar las contribuciones individuales dentro de actividades grupales.
Paso 8: Retroalimentación y evaluación. Proporciona retroalimentación a cada grupo sobre su desempeño. Evalúa las contribuciones grupales y brinda comentarios constructivos para fomentar la mejora continua.
Problemas de ecuaciones lineales con dos incógnitas basadas en contextos reales (dos ejemplos)
Problema 1: Camisetas deportivas
Un negocio de venta de camisetas deportivas tiene dos tipos de camisetas: las básicas, que se venden a $15 cada una, y las premium, que se venden a $25 cada una. El dueño del negocio vendió un total de 60 camisetas en un día, obteniendo $1200 en ventas. ¿Cuántas camisetas básicas y cuántas premium se vendieron ese día?
Ecuación: x y 𝑦 la cantidad de camisetas básicas y premium vendidas, respectivamente. La primera ecuación representa la cantidad total de camisetas vendidas: x + y = 60 (Ya que se vendieron 60 camisetas en total).
La segunda ecuación representa el total de ingresos por las ventas: 15x + 25y = 1200
(Ya que cada camiseta básica se vende a $15 y cada camiseta premium a $25, con un total de $1200 en ventas).
Preguntas Reflexivas para los Estudiantes:
¿Qué variables representan x y y en este problema y por qué son importantes? ¿Cómo puedes interpretar la primera ecuación en términos del contexto del problema Qué representa la segunda ecuación y por qué es relevante para resolver este problema? ¿Qué estrategias matemáticas podrías utilizar para resolver este sistema de ecuaciones? ¿Por qué elegirías esas estrategias? ¿Qué significa la solución al sistema en el contexto de este problema? ¿Cómo podrías verificar si tu solución es correcta?
Problema 2: Mezcla de café.
En una cafetería, se mezclan dos tipos de café: uno que cuesta $10 por libra y otro que cuesta $15 por libra. Se desea obtener una mezcla de 20 libras que cueste $12 por libra. ¿Cuántas libras de cada tipo de café se deben mezclar?
Ecuación: Sean 𝑥 y 𝑦 la cantidad de libras del primer y segundo tipo de café, respectivamente. La primera ecuación representa la cantidad total de café deseado: x + y = 20 (ya que se desea una mezcla de 20 libras en total).
La segunda ecuación representa el costo promedio por libra: 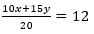
(ya que se busca obtener una mezcla que cueste $12 por libra).
Preguntas reflexivas para los estudiantes.
¿Qué representan x y y en este problema y por qué son importantes? ¿Cómo interpreta la primera ecuación en términos de la cantidad total de café? ¿Qué significa la segunda ecuación y por qué es relevante para resolver este problema? ¿Cuál sería tu enfoque para resolver este sistema de ecuaciones? ¿Por qué eliges esa estrategia? ¿Cómo validarías tu solución en términos del contexto del problema? ¿Por qué es importante encontrar la cantidad específica de cada tipo de café?
Resultados de la propuesta
Luego de aplicar la estrategia, se realizó una encuesta entre los estudiantes para conocer su opinión sobre la efectividad de la estrategia didáctica basada en Moodle en la enseñanza de ecuaciones lineales con dos incógnitas. Los resultados se presentan a continuación, ver tabla 8:
Tabla 8 - Efectividad de los recursos multimedia en Moodle.
| ¿Cuáles de los recursos multimedia a continuación proporcionados en Moodle facilitaron tu comprensión de los conceptos matemáticos? | Sí | No | ||
| f
|
f
|
f
|
f
|
|
| Videos | 51 | 93 | 4 | 7 |
| Presentaciones | 49 | 89 | 6 | 11 |
| Imágenes | 12 | 22 | 43 | 78 |
| Total | 112 | 68 | 53 | 32 |
| ¿Las actividades grupales en Moodle te permitieron interactuar con tus compañeros para resolver problemas de ecuaciones lineales con dos incógnitas? | 52 | 95 | 3 | 5 |
| ¿Las pruebas, cuestionarios o actividades de evaluación en Moodle te ayudaron a identificar tus áreas de mejora en matemáticas? | 33 | 60 | 22 | 40 |
| ¿Consideras que las actividades en Moodle se ajustaron a tu ritmo de aprendizaje y nivel de habilidad en matemáticas? | 52 | 95 | 3 | 5 |
| ¿Las retroalimentaciones recibidas en tus tareas o ejercicios en Moodle te ayudaron a mejorar tu comprensión de los temas de matemáticas? | 49 | 89 | 6 | 11 |
Fuente: elaboración propia.
De lo anterior se puede resumir que los estudiantes consideran que:
Los videos (93%) y las presentaciones (89 %) facilitaron su comprensión de los conceptos sobre las ecuaciones líneas de dos incógnitas y en menor medida las imágenes (22 %).
El 95 % de los estudiantes afirmó que la plataforma Moodle ha sido efectiva para facilitar la interacción entre los estudiantes.
Las evaluaciones en la plataforma han pretendido ser beneficiosas para el autoconocimiento y la reflexión de los estudiantes en su aprendizaje matemático, sin embargo, solo el 60% de los estudiantes considera que las pruebas, o actividades de evaluación general en Moodle les ayudaron a identificar sus áreas de mejora en matemáticas.
El 95 % consideró que las actividades en Moodle se ajustaron a su ritmo de aprendizaje y nivel de habilidad en matemáticas para la solución de problemas de ecuaciones lineales con dos incógnitas.
El 89% consideró que sus tareas o ejercicios en Moodle les ayudaron a mejorar su comprensión de las ecuaciones lineales con dos incógnitas yhan contribuido significativamente al refuerzo y comprensión de estos conceptos matemáticos.
Por último, se aplica a los 10 docentes seleccionados el Índices de Promotores Netos (NPS). Estos docentes están implicados con la experiencia y, por tanto, pueden ser usuarios reales o potenciales de la aplicación, capaces de evaluar y generalizar lo alcanzado. La aplicación de este índice consiste en realizar una pregunta con escala de 0 (malo) a 10 (excelente) consistente en: ¿Usted está tan satisfecho con la experiencia de la estrategia que consideraría en recomendarla para su generalización?
Los resultados obtenidos muestran que las votaciones resultaron: De 10 = 4 docentes; De 9 = 4; 8 = 1; 7= 1 y de 0 a 6= 0. Los docentes con evaluaciones de 9 y 10 se consideran promotores, los que la evalúan de 7 y 8 neutros y aquellos con votación inferior a 6 detractores. El índice resulta de la resta del porcentaje de promotores, menores detractores, por tanto, 80 unidades porcentuales, superior a las 50 unidades exigidas y se demuestra que la estrategia aceptada y se recomienda por los encuestados.
Conclusiones
Se desarrolla una estrategia didáctica con apoyo Moodle para la enseñanza de problemas de sistema de ecuaciones con dos incógnitas para los estudiantes de primero de bachillerato en la Unidad Educativa Réplica Nicolás Infante Díaz, caracterizada por un proceso de enseñanza aprendizaje basado en las teorías constructivistas y que facilite la comprensión de conceptos abstractos, promueva la participación activa, la aplicación práctica y la construcción de significado en los estudiantes.
Los resultados sobre la efectividad de la estrategia didáctica con apoyo Moodle para la enseñanza de ecuaciones lineales de dos incógnitas muestra una preferencia por los recursos multimedia, especialmente videos y presentaciones, el 95 % de los estudiantes afirmó que la plataforma Moodle les permitió ajustarse a su ritmo de aprendizaje y nivel de habilidad y el 89 % consideró que sus tareas o ejercicios les ayudaron a mejorar su comprensión. Sin embargo, a pesar de notarse mejoría en el tratamiento de las evaluaciones aún se aprecian reservas sobre las que se debe trabajar.
La aplicación del Índices de Promotores Netos (NPS) a docentes implicados y considerados usuarios reales o potenciales al ser capaces de evaluar y generalizar lo alcanzado, determinaron la diferencia de 80 unidades porcentuales, superior a las 50 unidades exigidas y se demuestra que la propuesta es aceptada y se recomienda por los docentes implicados.














