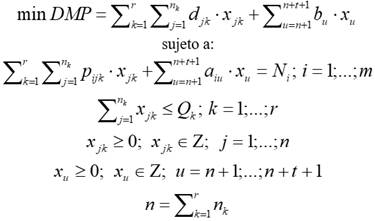Introducción
El corte de materiales es un proceso que el hombre lleva a cabo desde que empezó a utilizar los recursos que le brinda la naturaleza para explotarlos en su beneficio. En tiempos antiguos el corte no presentaba mayores dificultades, puesto que los materiales eran escasos y las necesidades humanas, en relación con la diversidad de objetos, eran pequeñas. Muchas veces el material era escogido justamente por sus dimensiones, lo que eliminaba la necesidad de cortarlo. Con la llegada de la Revolución Industrial el corte de materiales toma mayor importancia, la producción pasa de pequeños talleres a grandes empresa y fábricas, incorporándose máquinas especializadas destinadas a aumentar la eficiencia productiva. El corte de materiales comienza a aparecer en el diario de estas fábricas.
Se manifiestan fundamentalmente tres formas diferentes de realizar el corte de materiales: corte considerando sólo una dimensión del material a cortar y las piezas a obtener, corte considerando dos dimensiones del material a cortar y las piezas a obtener y corte considerando tres dimensiones del material a cortar y las piezas a obtener. El corte en una, dos y hasta tres dimensiones puede aplicarse a cualquier material, es el hombre quien decide qué tipo de corte realizar, según sus necesidades.
En el corte de materiales se toman en cuenta tres aspectos fundamentales: materia prima, piezas que se desean obtener y forma de realizar los cortes o variantes de corte a llevar a cabo. La materia prima se define como cualquier material que necesite ser cortado. En general, consiste en materiales procesados industrialmente con tamaños estándares a fin de proveer a la mayor cantidad de clientes. Una vez que la materia prima se encuentra en las entidades, esta es cortada en las piezas que realmente son necesarias para el desarrollo del proceso productivo de las mismas. Existen diferentes combinaciones para realizar el corte de la materia prima, estas dependen de las dimensiones a tomar en cuenta para realizar el corte y de las dimensiones de cada pieza a obtener. Esas diferentes formas o combinaciones posibles, se denominan variantes de corte. Este proceso lleva consigo el acarreo de desperdicio de material o lo que se entiende como sobrantes que no tienen ninguna utilidad práctica.
El corte considerando dos dimensiones (de forma rectangular), de interés en este trabajo, es aquel en el que se corta un material rectangular, teniendo en cuenta sólo dos de sus dimensiones, largo y ancho. Por ejemplo, el corte en piezas rectangulares de vidrios o espejos, tablas o tableros de madera y cartones o pliegues de papel, entre otros ejemplos.
Desarrollo
El proceso de corte en dos dimensiones supone un alto grado de complejidad y experiencia por parte del personal que lo realiza puesto que pueden existir diferentes formas de llevar a cabo los cortes en dependencia de las dimensiones de la materia prima y las cantidades, y dimensiones de las piezas a obtener; además, se debe ejecutar aquellas combinaciones de corte que menor desperdicio posible genere.
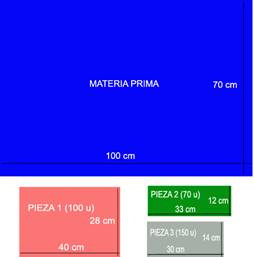
A continuación, se expone un ejemplo de pequeña magnitud para ilustrar esta situación. Se cuenta con unidades suficientes de una materia prima de 100 cm por 70 cm y se desean obtener 100 piezas tipo 1 de 40 cm por 28 cm, 70 piezas tipo 2 de 33 cm por 12 cm y 150 piezas tipo 3 de 30 cm por 14 cm (Fig. 1).
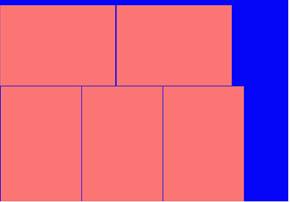
Una forma tradicional de ejecutar estos cortes consiste en cortar cada unidad de materia prima en la mayor cantidad de piezas de un tipo determinado (Fig. 2).

Fig. 2 Corte de una unidad de materia prima en la mayor cantidad de piezas posibles de un tipo determinado.
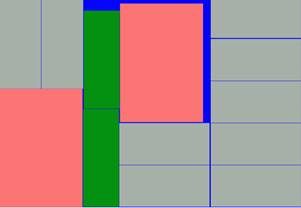
Este procedimiento es complejo puesto que puede ocurrir que existan otras combinaciones que garanticen un mejor uso de la materia prima, como por ejemplo el acomodo de 5 piezas de tipo 1 en lugar de 4 (Fig. 3).
Realizar los cortes de esta forma resulta, además, en la mayoría de los casos, ineficiente puesto que el acomodo mediante la combinación de distintos tipos de piezas puede garantizar un mejor uso de la materia prima (Fig. 4).
Las cantidades por tipos de piezas a obtener dificulta el proceso, aumentando la complejidad, con la incorporación de diferentes dimensiones de materias primas o restricciones de existencia para las unidades de las mismas.
Estos problemas pueden ser modelados matemáticamente utilizando la programación lineal en enteros (PLE) (Gilmore & Gomory, 1963; Rönnqvist, 1995). Cada patrón de corte se convierte en una variable del modelo, la función objetivo a minimizar se forma con los desperdicios de cada patrón de corte y las restricciones se componen con las demandas por tipo de pieza y las cantidades que aparecen en aquellos patrones de corte que incluyen dichas piezas (Collazo & Lahoz, 2009).
El caso específico de problemas de corte en dos dimensiones, ha presentado los siguientes inconvenientes: falta de un algoritmo para la generación de las variantes de corte (debido a su gran complejidad), modelo PLE con gran número de variables (debido al gran número de variantes de corte que se pueden presentar) y grandes requerimientos de recursos computacionales y/o de tiempo respectivamente en el procesamiento del modelo (debido a la naturaleza de estos modelos y de los métodos de solución).
Trabajos realizados en la Universidad de Cienfuegos en conjunto con la Pontificia Universidad Católica del Ecuador permiten contar con un algoritmo para la generación de variantes de corte en dos dimensiones de piezas rectangulares (Leiva Cáceres, 2018) y con una modelación alternativa a la modelación clásica de estos problemas que incorporan una propiedad poco utilizada, que permite disminuir la cantidad de patrones de corte haciendo uso de variantes de sustitución (De León Rodríguez, 1996). Estas variantes se forman “de combinar una pieza sustituyéndola por las de longitud menor que ella” (De León Rodríguez, 1996). El sistema de restricciones se representa mediante ecuaciones y presenta compatibilidad en el mismo, una de las ventajas que brinda el uso de las variantes de corte de sustitución.
La modelación matemática utilizada en el presente trabajo se define de la siguiente manera (ecuación 1):
Ecuación 1. Modelo matemático de PLE para el corte de materiales.
donde:
n: |
Cantidad de variantes de corte. |
m: |
Cantidad de piezas. |
r: |
Cantidad de tipos de longitudes de materia prima. |
Q k : |
Cantidad de unidades de materia prima de longitud tipo k. |
j: |
Índice de la variante de corte. |
i: |
Índice de la pieza. |
k: |
Índice del tipo de longitud de la materia prima. |
N i : |
Necesidad de piezas tipo i. |
DMP: |
Desperdicio de materia prima. |
d jk : |
Desperdicio de materia prima de longitud tipo k según la variante de corte j. |
P ijk : |
Cantidad de piezas tipo i que se obtienen al cortar una unidad de materia prima de longitud tipo k según la variante de corte j. |
x jk : |
Cantidad de materia prima de longitud tipo k que es necesario cortar según la variante de corte j. |
Z: |
Conjunto de los números enteros. |
u: |
Índice de la variante de sustitución. |
t: |
Cantidad de variantes de sustitución. |
x uk : |
Utilización de la variante de sustitución u en la materia prima de longitud tipo k. |
b uk : |
Desperdicio de materia prima de longitud tipo k generado por la variante de sustitución u. |
a iuk : |
Coeficiente de utilización de la pieza i en la variante de sustitución u para la materia prima de longitud tipo k. |
n k : |
Cantidad de variantes de corte para la materia prima de longitud tipo k. |
Este modelo se procesa para obtener la solución óptima. Esta solución se define como el “conjunto de patrones de corte que al ser ejecutados satisfacen la necesidad mínima por tipo de pieza teniendo presente la cantidad de materia prima disponible y con el mínimo desperdicio” (De León Rodríguez, 1996). Para la obtención de esta solución, expresada en valores enteros, se utiliza métodos de solución de programación lineal en enteros (Dantzig, 2016).
Los problemas de corte, abordados en el presente trabajo, utilizan modelos de PLE puros, puesto que todas las variables, definidas como: cantidad de materia prima a cortar siguiendo una determinada variante de corte, deben tomar valores enteros. Estos problemas de programación en enteros a simple vista pudieran parecer sencillos. Conociendo además la relativa facilidad con la que están resueltos los problemas continuos utilizando el método simplex (Hillier & Lieberman, 2002), se puede pensar que un problema en enteros no es más que un problema continuo donde se aplica un redondeo en la solución final. “Sin embargo, es necesario tener en cuenta que este redondeo puede conducir a soluciones no factibles que distan mucho de la solución óptima entera” (Felipe, 1983).
Un algoritmo de solución popular de estos modelos es el método de Branch and Bound, el cual es utilizado en el presente trabajo. Este método busca la solución óptima entera del problema lineal utilizando los métodos simplex (entiéndase simplex y dual) de forma iterativa. Una vez que se encuentra la solución al problema continuo, se añaden restricciones al mismo, las cuales se interpretan como ramificaciones respecto a los valores de las variables que requieren ser enteras, definiéndose dos nuevos problemas. La búsqueda termina cuando se halla una solución entera que no pueda ser superada o cuando se desarrollan todas las soluciones posibles y estas resultan no factibles, en este caso el método no tiene solución (Collazo & Lahoz, 2009).
Este método se interpreta como un árbol de soluciones, donde cada rama lleva a una posible solución posterior a la actual, con la característica de que se encarga de detectar en qué ramificación las soluciones dadas ya no están siendo óptimas, para no seguir desarrollando esa rama y no malgastar recursos y procesos (Boyd & Mattingley, 2007).
El algoritmo comienza con una relajación del problema y construye un árbol de soluciones, ramificándose aquellas fraccionarias que sean factibles. Las no factibles son acotadas. Cada solución entera factible es tomada como candidata a ser óptima sustituyendo, si existe, a la anterior. La última solución entera que se almacena es la óptima. La complejidad de este algoritmo es exponencial, aunque en ocasiones al acotar y ramificar se puede encontrar relativamente rápido las soluciones. El hecho de descomponer puede llevar a problemas de gran tamaño.
En la Universidad de Cienfuegos, durante la década del 90, surgen trabajos para el corte en una dimensión a partir de la utilización de métodos matemáticos, con el fin de disminuir la cantidad de variables en estos problemas, garantizando el sentido matemático de los mismos (De León Rodríguez, 1996). Con el fin de apoyar estos trabajos se crean sistemas que calculan las variantes de corte y reducen de manera significativa las mismas, siendo esto de gran ayuda en la modelación matemática de estos problemas.
Luego, en el año 2008, como parte del perfeccionamiento de estos sistemas, y el auge de las nuevas tecnologías se desarrolla el sistema informático OPTIVACORTUNI. Este programa, realizado para problemas de corte en una dimensión, integra en un solo producto: la generación de variantes de corte y de sustitución, la eliminación de variantes de corte dependientes, la modelación matemática del problema, el procesamiento computacional del modelo matemático y la interpretación económica de la solución óptima a través de un reporte totalmente entendible por los usuarios que permite orientar cómo se debe llevar a cabo el corte de materiales garantizando el desperdicio óptimo (Medina Mendieta, 2008).
En el año 2018, con la colaboración de la Pontificia Universidad Católica del Ecuador, se incorpora el módulo de corte en dos dimensiones y se crea el sistema informático, OPTIVACOMULTI, el cual mantiene lo mismo que el sistema OPTIVACORTUNI e incorpora la generación de las variantes de corte en dos dimensiones para piezas rectangulares, la modelación matemática de estos problemas, el procesamiento computacional y la interpretación de los resultados en un reporte gráfico (Leiva Cáceres, 2018).
El nombre OPTIVACOMULTI hace referencia a optimización de variantes de corte multidimensionales (Fig. 5). Este software especializado en encontrar solución a problemas de corte en una y dos dimensiones integra la generación de variantes de corte primarias y de sustitución para los casos de una y dos dimensiones, la búsqueda de dependencias entre las variantes de corte, la eliminación de aquellas variantes de corte dependientes, la construcción del modelo matemático, el procesamiento computacional del modelo matemático y, por último, y como aporte significativo, la interpretación de la solución óptima del modelo.
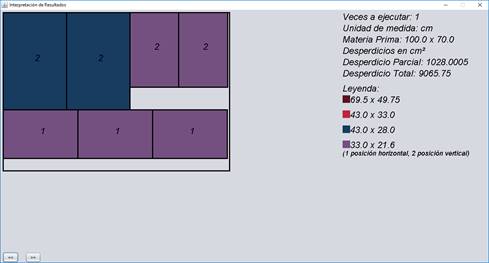
El sistema informático facilita el desarrollo de tareas que pudieran resultar de difícil realización debido a los conocimientos que suponen y/o a la magnitud de las mismas. A continuación se relacionan algunas de estas funcionalidades (Leiva Cáceres, 2018): preparación del modelo matemático una vez que se tienen las variantes de corte independientes (lo hace internamente y lo muestra al usuario, si este lo desea), procesamiento del modelo en un módulo interno (los datos los maneja internamente y en la mayoría de los casos son un gran volumen) e interpretación de los resultados (emite un reporte práctico expresado en un lenguaje en total correspondencia con el utilizado en el plan de corte a ejecutar por los operarios (Fig. 6).
Este sistema ha sido utilizado por la empresa poligráfica de Cienfuegos en el corte de pliegues de cartulinas de dimensiones estándares a gran escala, reduciendo significativamente desperdicios y por tanto influyendo positivamente en la economía de esta empresa.
Metodología
El proceso de corte de pliegues de cartulinas en la empresa poligráfica de Cienfuegos, Cuba se realizaba, antes del presente trabajo, de forma tradicional. El jefe de producción le entregaba a los operarios o cortadores el plan de corte, que comprendía las dimensiones de las piezas a cortar y la cantidad a obtener por cada tipo. Los operarios desarrollaban la labor a partir de su experiencia empírica, incurriendo, sin proponérselo, en desperdicios significativos.
En la primera década del 2000 se realizaron trabajos en conjunto con la Universidad de Cienfuegos de manera que para obtener la planeación y control del corte de un plan determinado se utilizaba la asistencia de personal especializado del Departamento de Matemáticas de este centro llevando a cabo la obtención de un gran número de variantes de corte, (sin garantizar la obtención de todas las posibles variantes de corte) la modelación matemática del problema, el procesamiento del mismo y la interpretación de los resultados.
Este proceso, realizado por profesores de la universidad y personal de la empresa Poligráfica, resultaba extenso, no exento de errores y demoraba, en ocasiones, días. Por estos motivos en la segunda década del actual siglo la empresa Poligráfica volvió a realizar el corte de pliegues de forma tradicional, incurriendo en el aumento de desperdicios, debido, fundamentalmente, a que el jefe de producción presentaba dificultades en la unión de la modelación matemática del problema, el procesamiento computacional del modelo matemático y la interpretación económica de la solución óptima del modelo.
A partir del 2018 se le propone a la empresa Poligráfica la utilización de la herramienta OPTIVACOMULTI que integra internamente: la generación de las variantes de corte en dos dimensiones de piezas rectangulares, la modelación matemática, procesamiento del modelo e interpretación de los resultados. Este sistema no necesita de personal especializado en matemática para su operación, lo cual posibilita que el propio jefe de producción pueda ser un usuario del sistema y pueda obtener en tiempo, relativamente corto, la planificación del corte para su futuro control, de forma que el desperdicio sea el menor posible.
Refieren directivos de la empresa Poligráfica de Cienfuegos que los desperdicios obtenidos en la realización de grandes planes de corte, luego de la utilización del sistema, disminuye la cantidad de materias primas (pliegues de cartulinas rectangulares de 100 cm por 70 cm) que son finalmente extraídas de almacén para ser cortadas, en comparación con los años, que el mismo plan de corte, se realizaba de forma empírica o con la asistencia de profesores de la Universidad. Como constancia han referido avales a los autores de este trabajo.
A continuación, se exponen resultados obtenidos en el corte de diferentes pliegues de cartulina rectangulares de alta calidad, de dimensiones estándar para la encuadernación de libros. En este estudio se utilizó como materia prima pliegues de dimensión 100 cm por 70 cm que se encontraba en explotación en ese momento. Las piezas a obtener fueron cartones rectangulares con los cuales se conformaron carátulas de libros. Las dimensiones diversas de estas carátulas dependieron de los distintos libros, que en ese momento se deseaban encuadernar.
Se estudiaron los desperdicios obtenidos por 15 planes de corte cuando el corte fue llevado a cabo de forma empírica por los cortadores, cuando fue resultado del intercambio científico del personal del Departamento de Matemáticas de la Universidad de Cienfuegos con la empresa Poligráfica y cuando fue resultado de la utilización del programa OPTIVACOMULTI.
Se utilizó la estadística inferencial, a partir de un enfoque no paramétrico para la comparación de varias muestras relacionadas y se aplicó la prueba de comparación de rangos de Friedman para muestras relacionadas (Berlanga & Rubio Hurtado, 2012).
Resultados y experimentación
De manera seguida, se presentan resultados obtenidos sin y con la utilización del sistema OPTIVACOMULTI en la empresa Poligráfica de Cienfuegos, Cuba. La Tabla 1 presenta el desperdicio, dado en cm2, obtenido en 15 planes de corte estudiados para cada uno de los tres casos referenciados anteriormente.
Tabla 1 - Desperdicios obtenidos sobre planes de corte ejecutados de diferentes formas.
| Plan de corte | Desperdicio obtenido al realizar el corte de forma empírica. | Desperdicio obtenido al realizar el corte asistido por personal especializado. | Desperdicio obtenido al realizar el corte utilizando el software Optivacomulti |
|---|---|---|---|
| 1 | 950,69 | 653,50 | 653,50 |
| 2 | 1350,25 | 1050,70 | 797,50 |
| 3 | 4346,26 | 1244,50 | 1244,50 |
| 4 | 3602,46 | 2340,86 | 1187,00 |
| 5 | 2939,28 | 2139,28 | 1269,00 |
| 6 | 3126,76 | 2426,76 | 1556,00 |
| 7 | 3348,69 | 2948,69 | 2078,50 |
| 8 | 2716,96 | 2316,96 | 1447,00 |
| 9 | 3070,12 | 2670,12 | 1569,50 |
| 10 | 3223,79 | 2823,79 | 1954,00 |
| 11 | 2152,81 | 1752,81 | 663,00 |
| 12 | 3524,54 | 2146,54 | 1154,92 |
| 13 | 2460,00 | 1568,42 | 1285,42 |
| 14 | 3566,85 | 1485,00 | 1485,00 |
| 15 | 4005,05 | 2642,05 | 1664,17 |
La Tabla 2 muestra el resultado de la prueba de Friedman. Se obtuvo una significación asintótica menor que 0,050, por lo que se puso de manifiesto que el desperdicio fue diferente en al menos uno de los tres casos.
Tabla 2- Prueba de Friedman.
| Estadísticos de contrastea | ||
| N | 15 | |
| Chi-cuadrado | 28,737 | |
| gl | 2 | |
| Sig. asintót. | ,000 | |
| a. Prueba de Friedman | ||
La Tabla 3 muestra la prueba de comparación de rangos tomados dos a dos por tratamiento. Se pone de manifiesto que el desperdicio difiere significativamente en dependencia de la forma en que fueron ejecutados los cortes, de manera que el desperdicio obtenido como promedio al utilizar el software OPTIVACOMULTI fue inferior al obtenido cuando se utilizó la asistencia de investigadores del Departamento de Matemáticas de la Universidad de Cienfuegos y este, a su vez, fue inferior al obtenido cuando el corte se realizó de forma empírica.
Tabla 3- Prueba de comparación de múltiples rangos.
| Tratamiento | Suma (Rangos) | Media (Rangos) | N | Grupos | |||
|---|---|---|---|---|---|---|---|
| Desperdicio obtenido al realizar el corte utilizando el software Optivacomulti | 16,50 | 1,10 | 15 | A | |||
| Desperdicio obtenido al realizar el corte asistido por personal especializado | 28,50 | 1,90 | 15 | B | |||
| Desperdicio obtenido al realizar el corte de forma empírica | 45,00 | 3,00 | 15 | C | |||
| Medias de rangos con letras distintas, difieren significativamente (p < 0,050) | |||||||
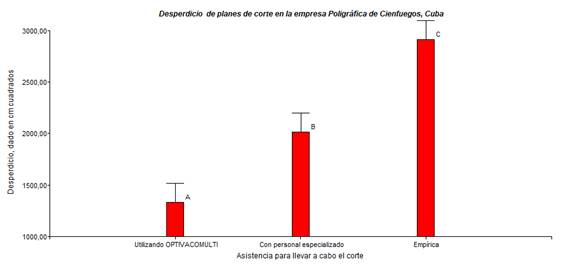
La Fig. 7 muestra los desperdicios promedios obtenidos al utilizar diferentes formas de ejecutar los planes de corte en la empresa Poligráfica de Cienfuegos, Cuba. El desperdicio obtenido utilizando el software OPTIVACOMULTI, realizado a tales efectos, difiere significativamente con respecto al desperdicio obtenido cuando no es utilizado este sistema.
Conclusiones
El proceso de corte de pliegues de cartulina en la empresa Poligráfica de Cienfuegos, Cuba, en piezas rectangulares, acarrea desperdicios que es de interés optimizar. Desde la modelación matemática pueden ser abordados estos problemas de forma que se optimice la materia prima. Debido a la gran magnitud de estos problemas, la utilización de diferentes herramientas para resolver un problema y la falta de preparación para implementar los mismos por parte del personal vinculado a esta actividad, se ha venido realizando de forma tradicional sin tomar en cuenta la modelación matemática y la no optimización de la materia prima.
El uso de un programa computacional creado a tales efectos que integre la generación de las variantes de corte en dos dimensiones, la modelación matemática del problema, el procesamiento computacional del modelo matemático y la interpretación de la solución óptima del mismo permite disminuir desperdicios influyendo positivamente en la organización y control de estos procesos.