ARTÍCULO ORIGINAL

 

Análisis del uso de las bibliotecas gsl y lapack en la construcción de árboles filogenéticos

 

Analysis of the use of gsl and lapack libraries in building phylogenetic trees

 

 

Leonardo Del Toro Melgarejo^1*, Daniel Gálvez Lio¹, Ricardo Sánchez Alba²

¹ Departamento de Computación, Universidad Central Marta Abreu de Las Villas, Carretera a Camajuaní Km 5 ½ Santa Clara Villa Clara Cuba C.P: 54830. Correo-e: [e-mail]
² Facultad de Matemática, Física y Computación, Universidad Central Marta Abreu de Las Villas, Carretera a Camajuaní Km 5 ½ Santa Clara Villa Clara Cuba C.P: 54830. Correo-e: [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

Un árbol filogenético o árbol de la evolución es un diagrama de ramificación o "árbol" que muestra las relaciones evolutivas entre las diferentes especies biológicas sobre la base de similitudes y diferencias en sus características físicas o genéticas. En el estudio del proceso evolutivo se emplean, entre otros, los métodos para construir árboles filogenéticos basados en la distancia genética entre parejas de secuencias de ADN o proteínas, que requieren un alineamiento múltiple como información de entrada. En estos, los datos utilizados se presentan en una matriz de distancias obtenida a partir del alineamiento de las secuencias, de acuerdo a algún modelo biológico. Algunos de estos métodos se basan en el criterio de mínima evolución, donde el mejor árbol es aquel que minimiza la longitud de las ramas internas. Para encontrar este árbol se puede emplear un método de ajuste basado en los mínimos cuadrados (LS). Este ajuste se emplea para estimar las longitudes de las ramas entre todas las topologías posibles, seleccionando aquella que minimice tanto como sea posible la diferencia entre la distancia dada y la pronosticada. Su solución es analítica, y puede obtenerse a partir de un sistema de ecuaciones lineales. Para resolver estos sistemas existen múltiples bibliotecas matemáticas. Entre ellas, la biblioteca GSL brinda una interfaz más confortable, mientras que la biblioteca LAPACK presenta un rendimiento superior. En este trabajo se comparan los resultados obtenidos al emplear ambas bibliotecas en la implementación del método LS para la construcción de árboles filogenéticos.

Palabras clave: árbol, bibliotecas, filogenética, gsl, lapack, mínimos cuadrados.

---

ABSTRACT

A phylogenetic tree or evolutionary tree is a branching diagram or "tree” showing the evolutionary relationships among various biological species based on similarities and differences in their physical or genetic characteristics. In the study of the evolutionary process, several methods are used to construct phylogenetic trees, including those based on the genetic distance between pairs of DNA sequences or proteins, which require a multiple alignment as input. In such methods, the data used are presented in a distance matrix obtained from the alignment of the sequences according to a biological model. The criterion of minimum evolution is one of these methods, where the best tree is one that minimizes the length of the internal branches. To find this tree can be used an adjustment method based on least squares (LS). This adjustment is used to estimate the lengths of the branches between all possible topologies, selecting the one that minimizes as much as possible, the difference between the given and the predicted distance. Their solution is analytic and can be obtained from a system of linear equations. To solve these systems there are several math libraries. Between them, the GSL library provides a more comfortable interface, while the LAPACK library has a superior performance. In this paper, are compared the results obtained by using both libraries, in the implementation of the LS method for constructing phylogenetic trees.

Key words: gsl, lapack, least squares, libraries, phylogenetic, tree.

---

 

 

INTRODUCCIÓN

La filogenética computacional es la aplicación de algoritmos computacionales, en métodos y programas de análisis filogenético. El objetivo es construir un árbol filogenético que represente una hipótesis evolutiva de un conjunto de genes, especies u otros taxones. De esta manera podemos expresar las relaciones existentes entre ancestros y descendientes mediante la topología de un árbol.  La filogenética molecular actual usa secuencias de nucleótidos que codifican genes o secuencias de aminoácidos que forman proteínas como bases de la clasificación. Muchas formas de filogenética molecular están muy relacionadas y hacen un uso extensivo del alineamiento de secuencias en la construcción y redefinición de los árboles filogenéticos usados para la clasificación de las relaciones evolutivas entre los genes homólogos existentes en los genomas de especies divergentes.
 
El proceso de construcción de árboles filogenéticos es de gran importancia para el estudio de los procesos evolutivos en secuencias genéticas. Por ejemplo, la estimación de las tasas de mutación en una secuencia de DNA, dependen de la región del genoma y la posición de la base nitrogenada en el codón correspondiente, en los descendientes respecto a sus ancestros (Del Toro, et al., 2011).

Los métodos empleados para la construcción de árboles filogenéticos son varios. Los algorítmicos (clusters methods) obtienen un árbol único desde los datos como el mejor estimado del árbol real. Los basados en la optimalidad (search methods) emplean un criterio (función objetivo) para medir cuanto se ajusta el árbol a los datos, y el árbol con una mejor puntuación (score) de todos los obtenidos constituye la mejor estimación del árbol real. Entre los primeros encontramos a los métodos basados en distancias como UPGMA (Unweighted Pair-Group Method using arithmetic Averages) (Sokal y Sneath, 1963) y Neighbor Joining (NJ) (Saitou y Nei, 1987). Entre los segundos a: Máxima Parsimonia (MP) (Fitch, 1971, Hartigan, 1973), Máxima Verosimilitud (MV) (Felsenstein, 1981, Posada, 2008) , y los Bayesianos (MB) (Mau y Newton, 1997, Yang, 2006).

Los métodos basados en distancias permiten construir árboles filogenéticos basados en la distancia genética entre parejas de secuencias de ADN o proteínas, por lo que requieren un alineamiento múltiple como información de entrada. El alineamiento múltiple de secuencias es esencial en la mayoría de los análisis bioinformáticos que implican la comparación de secuencias homólogas. (Sievers, et al., 2011). A diferencia del resto de los métodos, que emplean el propio conjunto de secuencias o alineamiento, los de distancia utilizan como datos a una matriz de distancias obtenida a partir del alineamiento múltiple de las secuencias y de un modelo evolutivo determinado.

La principal ventaja de los métodos basados en distancias es su velocidad, lo que resulta de particular utilidad cuando se tiene un gran número de secuencias. Los problemas más importantes son la pérdida de información del alineamiento múltiple y la generación de un árbol único, por lo que se desechan árboles que podrían ser igualmente válidos y consistentes con los datos.

En (Del Toro, et al., 2011) se emplea un método basado en el criterio de mínima evolución, donde el mejor árbol es aquel que minimiza la longitud de las ramas internas. La longitud en el árbol se calcula generalmente, sumando la longitud de las ramas que a su vez son estimadas a través del método de los mínimos cuadrados (Cavalli-Sforza y Edwards, 1967). Este procedimiento, involucra dos pasos fundamentales: El cálculo de la distancia genética entre cada par de secuencias (matriz de distancias) de acuerdo a algún modelo biológico y la construcción de un árbol filogenético desde esta matriz.

El grupo de Bioinformática de la Universidad Central “Marta Abreu” de Las Villas (UCLV) ha desarrollado estudios acerca de la evolución de secuencias virales. En ellos se emplean diferentes modelos biológicos como el TN93 (Tamura y Nei, 1993) y el FBM (Sánchez y Grau, 2009) para calcular la distancia genética entre cada par de secuencias. Para estimar las tasas de mutaciones en secuencias por sitios, es necesaria la construcción previa de un árbol filogenético que exprese la relación evolutiva entre los mismos. Con ese propósito se ha empleado a la herramienta FASTME (Desper y Gascuel, 2002), que incorpora estrategias heurísticas como el intercambio de ramas (nearest-neighbour interchange, NNI) para la estimación del árbol, pero no garantiza obtener el mejor árbol.

Por ese motivo, se desarrolló un algoritmo para construir el árbol filogenético a partir de la matriz de distancias obtenida de acuerdo al modelo evolutivo seleccionado, que estima la longitud de las ramas entre cada par de secuencias genéticas empleando un criterio basado en los mínimos cuadrados (LS) (Del Toro, et al., 2011). Ese algoritmo, con una alta complejidad computacional garantiza encontrar el mejor árbol posible de acuerdo al criterio seleccionado. En su implementación se empleó a la biblioteca GSL (Gough, 2009), y se programó en lenguaje C. Alguno de los métodos brindados por la biblioteca, que fueron empleados para estimar las longitudes de las ramas (gsl_linalg_QR_decomp y gsl_linalg_QR_lssolve) mostraron tener un alto costo lo que incrementaba el tiempo empleado por la aplicación.

En este artículo, a partir de la problemática presentada por los métodos de la biblioteca GSL durante el proceso de solución a sistemas de ecuaciones lineales, se decidió sustituirlos por algún otro que fuese más eficiente. En la actualidad, las bibliotecas de software LAPACK (Anderson, et al., 1999) y ScaLAPACK (Choi, et al., 1996), representan el estándar de facto para los densos cálculos de álgebra lineal de alto rendimiento y se han desarrollado, respectivamente, para arquitecturas de memoria compartida y de memoria distribuida (Buttari, et al., 2008).

Con el propósito de lograr una aplicación que reduzca el tiempo empleado para construir el árbol filogenético, se introdujo el uso de la biblioteca LAPACK, accesible en: http://www.netlib.org/lapack. Al emplear el método (LAPACKE_dgels), se logra una disminución significativa del tiempo si se compara con la versión que usa la GSL.

Este artículo se encuentra estructurado como se describe a continuación: después de una breve introducción sobre el uso de bibliotecas matemáticas para construir árboles filogenéticos, en Materiales y Métodos se describe el método de los mínimos cuadrados, se expone el algoritmo propuesto para construir árboles filogenéticos, y se describen algunos métodos numéricos y bibliotecas, particularmente aquellos que permiten resolver sistemas de ecuaciones lineales usando las bibliotecas GSL y LAPACK. En Resultados y discusión, se presentan los resultados obtenidos por las aplicaciones ptb_ls y ptb_lapack, que usan las bibliotecas GSL y LAPACK, respectivamente. Finalmente, la última sección concluye este trabajo.

 

MATERIALES Y MÉTODOS

El método de los mínimos cuadrados (LS)

Constituye una técnica de análisis numérico enmarcada dentro de la optimización matemática, en la que, dados un conjunto de pares ordenados se intenta encontrar la función continua, que mejor se aproxime a los datos, de acuerdo con el criterio de mínimo error cuadrático.

En Biología Computacional, este método toma como datos de entrada a la matriz de distancias genéticas y estima las longitudes de las ramas de un árbol, haciendo coincidir esas distancias tanto como sea posible, minimizando la suma de las diferencias al cuadrado entre las distancias dadas y las pronosticadas.

La distancia pronosticada se calcula como la suma de las longitudes de rama a lo largo de la ruta de la conexión entre dos especies. La suma mínima de las diferencias al cuadrado, se emplea para medir el ajuste del árbol a los datos (las distancias) y se utiliza como la puntuación (score) del árbol (Yang, 2006).

Sea la distancia entre las especies i y j denominada como d_ij. A su vez, sea la suma de la longitud de las ramas a lo largo del camino entre las especies i y j en el árbol denotada como d´_ij. Este método minimiza la suma de las diferencias cuadradas (d_ij – d´_ij)², sobre todos los distintos pares i y j, de forma tal que el árbol se ajuste a estas distancias de la forma más cercana posible.

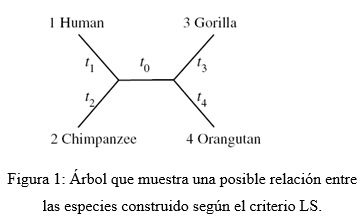
Suponga el árbol ((Human, Chimpanzee), Gorilla, Orangutan) de la figura 1 y sus cinco longitudes de ramas t₀, t₁, t₂, t₃, t₄. La distancia pronosticada entre la especie Human y Chimpanzee es t₁ + t₂, la pronosticada entre Human y Gorilla es t₁ + t₀ + t₃ , y así sucesivamente.

Para este árbol, según la expresión 1, la suma de las diferencias será:

 

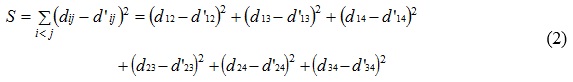
Las distancias (d_ij) ya fueron calculadas previamente y se obtienen de la matriz de distancias.  S es una función de cinco valores de longitud de rama desconocidos t₀, t₁, t₂, t₃, y t₄. El cálculo de la longitud de las ramas en un árbol usando el método LS se estima analíticamente y puede obtenerse a través de un sistema de ecuaciones lineales.

De manera similar se deben calcular los valores estimados para t₀, t₁, t₂, t₃, y t₄, de acuerdo a las tres posibles topologías de árbol restantes (de manera similar a la mostrada en la figura 1). De todos los scores obtenidos se selecciona la topología que minimiza S.

Algoritmo propuesto para la construcción del árbol filogenético

En (Del Toro, et al., 2011) se propone la construcción del árbol filogenético empleando al método LS a partir de una matriz de distancias genéticas. Esta matriz puede construirse empleando a algún modelo biológico. Para ello se propuso un algoritmo que construye un árbol filogenético lleno (full binary tree) adicionando un nodo interno por cada secuencia o especie que se desee insertar al subárbol construido en la etapa previa. Para cada una de ellas debe probarse su posible inserción en todas las posibles posiciones disponibles (hojas del árbol), seleccionando aquella que minimice S. El procedimiento se ilustra a través del algoritmo siguiente:

En el algoritmo se observa una complejidad computacional, inherente a los dos ciclos, de n². El primero asociado a la especie que se desea insertar al árbol (n_i), y el segundo refiere el nodo hoja seleccionado para la inserción (n_j).

Para determinar S_j, se estiman los valores de longitud de las ramas a través de un sistema de ecuaciones lineales. Típicamente la complejidad computacional de estos sistemas de ecuaciones es n³ (Descomposición QR). Así, el procedimiento completo tendrá una complejidad computacional de n⁵, la cual es significativamente alta.

Debido al alto costo que implica la solución al sistema se ecuaciones lineales, la selección del software a emplear en su implementación resulta en un elemento de vital importancia.

Métodos numéricos y bibliotecas

Actualmente la comunidad científica tiene acceso a múltiples métodos numéricos y bibliotecas. Estos se agrupan de acuerdo a determinadas categorías (https://www.westgrid.ca/support/software/math_libraries), y entre sus exponentes más importantes tenemos los siguientes:

• Bibliotecas matemáticas integrales (GSL - GNU Scientific Library, MKL - Intel Math Kernel Library).
• Solucionadores a ecuaciones diferenciales (PETSc - A toolkit for solution of differential equations with parallel solver, FFTW - A widely-used FFT implementation).
• Algebra Lineal (BLAS - Basic Linear Algebra Subprograms, LAPACK - Linear algebra subroutine package, ScaLAPACK - Scalable LAPACK).
• Estadística (R language).

En este grupo tenemos a GSL, que constituye una gran colección de rutinas para la computación científica, escrita en lenguaje en C. Por otro lado, LAPACK es una biblioteca transportable de subrutinas del lenguaje Fortran 77, para resolver los problemas más comunes en álgebra lineal numérica: sistemas de ecuaciones lineales, problemas de mínimos cuadrados lineales, problemas de valores propios y problemas de valores singulares. Ambas bibliotecas han sido ampliamente utilizadas por los programadores y se encuentran disponibles en los repositorios de las distribuciones Linux pertenecientes al proyecto GNU.

En el algoritmo propuesto previamente, es necesario determinar el valor de S_j, para lo cual es necesario realizar una factorización de matrices (solución analítica del sistema de ecuaciones lineales). En el álgebra lineal la factorización de una matriz es la descomposición de la misma como producto de dos o más matrices según una forma canónica.

Aunque existen varios métodos, el más empleado es la Factorización QR o triangularización ortogonal (Kurzak y Dongarra, 2009). La descomposición o factorización QR de una matriz es una descomposición de la misma como producto de una matriz ortogonal por una triangular superior. Esta presenta las características siguientes:

• Aplicable a una matriz A (m x n).
• Factorización: A = QR, donde Q es una matriz ortogonal (m x m), y R es una matriz triangular superior (m x n).
• Métodos de cálculo: La factorización QR puede calcularse mediante el proceso de ortogonalización de  Gram-Schmidt aplicado a las columnas de A, mediante el uso de transformaciones de Householder y mediante transformaciones de Givens.
• La factorización QR puede utilizarse para "resolver" el sistema de ecuaciones lineales Ax = b cuando el número de ecuaciones es distinto al de incógnitas.

La biblioteca GSL

La Biblioteca Científica GNU (o GSL) es una biblioteca de software para cálculos numéricos en matemáticas y ciencias aplicadas. Está escrita en C y sus paquetes están disponibles para otros lenguajes de programación (C++, Python, Fortran, Perl, R, entre otros). Es parte del Proyecto GNU y se distribuye bajo la Licencia Pública General GNU. El proyecto GSL se inició en 1996 y su objetivo era escribir un reemplazo moderno para las ampliamente utilizadas, pero algo obsoletas, bibliotecas de Fortran. La versión 1.0 fue lanzada en 2001.

En la actualidad la biblioteca continúa desarrollándose activamente y puede descargarse desde: http://www.gnu.org/software/gsl/. Su versión actual (1.16) fue lanzada en julio de 2013.
La biblioteca de software proporciona facilidades para: funciones matemáticas básicas, números complejos, polinomios, funciones especiales, vectores y matrices, permutaciones, transformada rápida de Fourier, generación de números aleatorios, integración Monte Carlo, ecuaciones diferenciales ordinarias, mínimos cuadrados ajustados, aritmética de punto flotante IEEE, entre otros.

• Funciones que realizan la descomposición QR:

El empleo de la biblioteca GSL para realizar la descomposición QR ha sido explorada en varios trabajos (Marthi y Chengalur, 2014, Širca y Horvat, 2012). Una matriz general rectangular A de dimensiones m x n, tiene una descomposición QR en el producto de una matriz ortogonal cuadrada Q (m x m) (donde Q^TQ = I) y una matriz triangular derecha

Esta descomposición se puede utilizar para convertir el sistema lineal Ax = b en el sistema triangular Rx = Q^Tb, que puede ser resuelto por sustitución regresiva. La descomposición QR se emplea además para calcular una base ortonormal para un conjunto de vectores. Aquí, las primeras n columnas de Q forman una base ortonormal para el rango de A, ran(A), cuando A tiene un rango de columna completo.

Para solucionar un sistema de ecuaciones lineales deben emplearse las dos funciones siguientes:

a) int gsl_linalg_QR_decomp (gsl_matrix * A, gsl_vector * tau)

Esta función factoriza la matriz A (m x n) en la descomposición QR (A = QR). Como salida, la parte triangular superior y diagonal de la matriz de entrada, contiene a la matriz R. El vector tau y las columnas de la parte triangular inferior de la matriz A contienen los coeficientes y vectores de Householder que codifican la matriz ortogonal Q.

El vector tau debe ser de longitud k =\min (m,n).

La matriz Q se relaciona con estos componentes por, Q = Q_k,..., Q_2, Q_1 donde:

Q_i = I - \tau_i v_i v_i^T 

y v_i es el vector de Householder,  v_i = (0,...,1, A(i+1,i), A(i+2,i), ... , A(m,i)).

Este es el mismo esquema de almacenamiento utilizado por LAPACK.

b) int gsl_linalg_QR_solve (const gsl_matrix * QR, const gsl_vector * tau, const gsl_vector * b, gsl_vector * x)

Esta función resuelve el sistema cuadrado Ax = b usando la descomposición QR de A realizada en (QR, tau), que se debe haber calculado previamente con gsl_linalg_QR_decomp. Esta función devuelve el vector x, como solución al sistema de ecuaciones presentado. La solución de mínimos cuadrados para sistemas rectangulares se puede encontrar utilizando gsl_linalg_QR_lssolve.

La biblioteca LAPACK

LAPACK (Linear Algebra Package) es una biblioteca de software para el álgebra lineal numérica. Proporciona rutinas para solucionar sistemas de ecuaciones lineales y mínimos cuadrados lineales, problemas de valores propios, y la descomposición de valor singular. También incluye rutinas para implementar las factorizaciones matriciales asociadas tales como LU, QR, Cholesky y la descomposición de Schur. LAPACK fue originalmente escrito en FORTRAN 77, pero se tradujo a Fortran 90 en la versión 3.2 (http://www.netlib.org/lapack/lapack-3.2.html). Las rutinas manejan ambos tipos de matrices, reales y complejas, tanto en simple como en doble precisión. La versión más actual es la 3.5.0, que fue lanzada en noviembre de 2013.

Las versiones más recientes de LAPACK, contienen una interfaz para utilizar LAPACK desde C, conocida como LAPACKE, accesible en: http://www.netlib.org/lapack/lapacke.html.

Esta biblioteca es usada ampliamente por su escalabilidad en soluciones computacionales (Agullo, et al., 2009, Khan, et al., 2013, Ordonez, et al., 2014) e incluye como características las siguientes:

• El nombre de las subrutinas tiene la forma LAPACKE_dsyev.
• La función retorna la información de los argumentos ya que estos no se encuentran en la lista de parámetros.
• Todos los parámetros se utilizan de una forma similar a C: sólo los arreglos son punteros.
• En general, hay dos versiones de una función: por ejemplo LAPACKE_dsyev y LAPACKE_dsyev_work. El primero determina el espacio de trabajo óptimo por sí mismo, el segundo espera que el espacio de trabajo sea proporcionado por quien la utiliza.
• Si uno o más parámetros son matrices de 2 dimensiones, se necesita un parámetro adicional: LAPACK_COL_MAJOR o LAPACK_ROW_MAJOR. La primera de ellas para el diseño de la matriz Fortran, el segundo para el diseño de la matriz C. Este se coloca delante de todos los demás parámetros.
• LAPACKE también se puede utilizar para llamar a subrutinas de la biblioteca LAPACK desde la biblioteca MKL de Intel.
  
  
  • Funciones que realizan la descomposición QR:

En esta biblioteca se emplean las subrutinas de la familia LAPACK DGELS, que fueron mejoradas en 2001 para matrices de cualquier dimensión (Elmroth y Gustavson, 2001). Los cuatro problemas diferentes de DGELS
Solución lineal de mínimos cuadrados para minimize ǀǀAX − BǀǀF (m ≥ n),
solución lineal de mínimos cuadrados para minimize ǀǀAT − BǀǀF (m < n),
solución de norma mínima para minimize ǀǀAT − BǀǀF (m ≥ n) y
solución de norma mínima para minimize ǀǀAX − BǀǀF (m < n)),
se reducen básicamente a dos, mediante el uso de una transposición explícita de A.

Con la transposición explícita evitamos el cómputo de transformaciones Householder en vectores con gran antelación. La factorización QR de columnas de bloques de A se realiza usando un algoritmo recursivo nivel-3. Intercalando actualizaciones de B con la factorización de A, se reduce el número de operaciones de punto flotante realizados por el problema lineal de mínimos cuadrados. Al evitar cálculos redundantes en la actualización de B se reduce el trabajo necesario para calcular la solución de norma mínima. Adicionalmente se incluyen algoritmos totalmente recursivos para los cuatro problemas de DGELS, así como para la factorización QR.

Para solucionar un sistema de ecuaciones lineales Ax = b, para matrices no simétricas, debe emplearse la función siguiente:

lapack_int LAPACKE_dgels (int matrix_order, char trans, lapack_int m, lapack_int n, lapack_int nrhs,   double *a, lapack_int lda, double *b, lapack_int ldb)

Donde:

• matrix_order: Indica cómo se almacenan los elementos de las matrices (vectores) en la memoria del computador. Su valor puede ser LAPACK_COL_MAJOR o LAPACK_ROW_MAJOR.
• trans: Indica cómo se resolverá el sistema lineal.

N: El sistema involucra a la matriz A (a)

• Si m>=n encuentra la solución de mínimos cuadrados para un sistema indeterminado (por ejemplo, minimize || B - AX ||).
• Si m<n encuentra la solución de norma mínima para un sistema indeterminado AX=B.

T: El sistema involucra a la matriz AT

• Si m>=n encuentra la solución de norma mínima para un sistema indeterminado ATX=B.
• Si m<n encuentra la solución de mínimos cuadrados para un sistema indeterminado (por ejemplo, minimize || B - ATX ||).
• m: Indica el número de filas de la matriz A.
• n: Indica el número de columnas de la matriz A.
• nrhs: Indica el número de columnas de la matriz B (b) y x.
• *a: La matriz A.
• lda: La dimensión principal de la matriz A (número de columnas de A para el estilo empleado en C).
• *b: La matriz (vector) B.
• ldb: La dimensión principal de la matriz B (número de columnas de B para el estilo empleado en C).

Esta función devuelve la matriz (vector) B, como solución al sistema de ecuaciones presentado.

 

RESULTADOS Y DISCUSIÓN

Evaluación y comparación de los resultados obtenidos

Para evaluar el desempeño del algoritmo propuesto, se decidió implementar una nueva aplicación (ptb_lapack) que fuese capaz de determinar el valor de Sj, empleando la biblioteca LAPACK (LAPACKE_dgels). Esta aplicación fue elaborada empleando el lenguaje de programación C y sus resultados fueron validados con la versión ya existente que utiliza la biblioteca GSL (ptb_ls) (Del Toro, et al., 2011).

En su desarrollo se utilizó la interfaz Netbeans 7.4, sobre la versión 7.4.0 del sistema operativo GNU/Linux Debian Wheezy.

Para comparar su desempeño, ambas aplicaciones fueron evaluadas con 3 juegos de datos (GenBank datasets) (Benson, et al., 2012) correspondientes a segmentos de la proteína HA del virus de la influenza humana A (2 al subtipo H1N1 y uno al subtipo H3N2 obtenidos del sitio NCBI (National Center for Biotechnology Information) accesible en: http://www.ncbi.nlm.nih.gov/genomes/FLU/Database/nph-select.cgi?go=database.

En el primer grupo, tenemos los archivos GeneFastaResults_HA.fas (alineamiento gen_fas, con 749 secuencias de 1702 nucleótidos) y FASTA_NA_Human.fas (alineamiento na_human, con 1000 secuencias de 1781 nucleótidos). El segundo grupo, es representado en el archivo FASTA_H3N2.fas (alineamiento h3n2, con 198 secuencias de 1765 nucleótidos). Sobre estos se realizó un proceso alineamiento múltiple empleando la herramienta clustalo, que puede descargarse desde: http://www.clustal.org/omega/.

Como etapa previa a la construcción del árbol filogenético, se construyeron las matrices de distancias correspondientes a cada alineamiento de acuerdo al modelo biológico TN93 (Tamura y Nei, 1993).

Las aplicaciones se ejecutaron en el centro de datos de la UCLV, accesible en: http://hpc.uclv.cu/, sobre nodos de cómputo del clúster que poseen dos procesadores Intel Xeon 5130, operando a 2.00 GHz y con 16 GB de memoria.

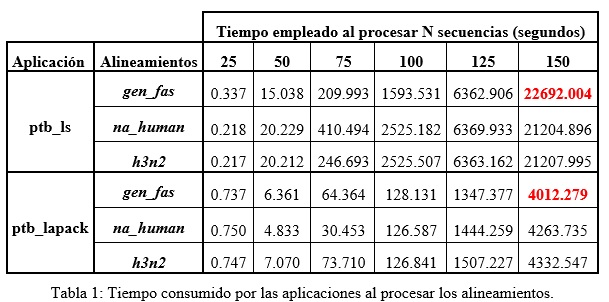
Los árboles filogenéticos construidos por ambas aplicaciones fueron comparados usando varias herramientas (Letunic y Bork, 2011, Zhang, et al., 2012), resultando ser iguales. La tabla 1 muestra el tiempo empleado por cada aplicación al procesar diferentes muestras de los conjuntos de datos.

En la tabla 1, se observa un comportamiento similar en tiempo durante el procesamiento de cada conjunto de datos según el número de secuencias (N). Este comportamiento se debe a la incidencia del modelo TN93 durante el proceso de construcción de la matriz de distancias genéticas. Este modelo, establece que aquellos sitios en secuencias alineadas que presenten ausencia de información (nucleótido desconocido o gap) deben ser descartados del análisis (Dalquen, et al., 2012, Kumar, et al., 2008).

Las bases de datos seleccionadas para el estudio presentan sitios con un número de gaps alto, y son superiores en los alineamientos gen_fas y na_human. Por este motivo, las dimensiones del problema a tratar por las aplicaciones son similares. No obstante, se observa que para 150 secuencias del alineamiento gen_fas, la aplicación ptb_lapack redujo su tiempo de ejecución en un factor de 5.656 respecto a la versión ptb_ls. Esto implica que el crecimiento exponencial en tiempo para ambas aplicaciones es menor en la versión que emplea LAPACK.

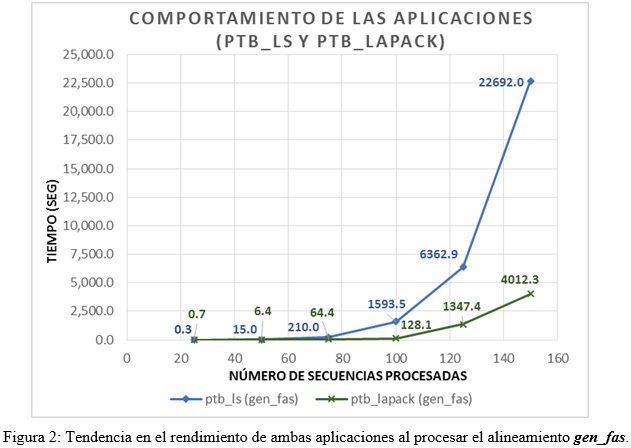
En la figura 2 se observa este comportamiento, que nos permite asegurar que un aumento en el número de secuencias a procesar hace mayor la diferencia entre ambas aplicaciones, generando un factor de ganancia aún superior.

De acuerdo a los resultados de la tabla 1 se deduce que en el procesamiento de los restantes conjuntos de datos se obtendría un comportamiento similar.

 

CONCLUSIONES

El algoritmo secuencial abordado presenta una complejidad computacional muy alta (n⁵), garantizando obtener el mejor árbol, siendo posible implementarlo utilizando diferentes bibliotecas para determinar las longitudes de las ramas que minimizan S_j. Los resultados experimentales muestran que la biblioteca LAPACKE presenta un mejor desempeño que la GSL para obtener las soluciones al sistema de ecuaciones lineales. El número de secuencias a procesar por las aplicaciones en los tres juegos de datos no incidió significativamente en el desempeño de las aplicaciones debido a que tratan con problemas de dimensiones similares. El empleo de funciones de la biblioteca LAPACK y similares, al tratar problemas que realicen procesamiento matemático analítico, debe considerarse como una de primeras estrategias durante el proceso de implementación. El manejo de estructuras de datos que requieran un alto consumo de recursos de memoria y por ende, de procesamiento, se favorece con la introducción de técnicas paralelas, empleando bibliotecas basadas en sistemas de memoria compartida, que reduzcan el costo de los algoritmos tratados.

 

REFERENCIAS BIBLIOGRÁFICAS

AGULLO, E.; HADRI, B.; LTAIEF, H. & DONGARRRA, J. Comparative study of one-sided factorizations with multiple software packages on multi-core hardware. En: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis. ACM, 2009, p. 20.

ANDERSON, E.; BAI, Z.; BISCHOF, C.; BLACKFORD, S.; DEMMEL, J.; DONGARRA, J.; DU CROZ, J.; GREENBAUM, A.; HAMMERLING, S. & MCKENNEY, A. LAPACK Users' guide, Society for Industrial and Applied Mathematics, 1999. 520 pp.

BENSON, D.A.; CAVANAUGH, M.; CLARK, K.; KARSCH-MIZRACHI, I.; LIPMAN, D.J.; OSTELL, J. & SAYERS, E.W. GenBank. Nucleic acids research, 2012: p. gks1195.

BUTTARI, A.; LANGOU, J.; KURZAK, J. & DONGARRA, J. Parallel tiled QR factorization for multicore architectures. Concurrency and Computation: Practice and Experience, 2008, 20 (13): p. 1573-1590.

CAVALLI-SFORZA, L.L. & EDWARDS, A.W. Phylogenetic analysis. Models and estimation procedures. American journal of human genetics, 1967, 19 (3 Pt 1): p. 233.

CHOI, J.; DEMMEL, J.; DHILLON, I.; DONGARRA, J.; OSTROUCHOV, S.; PETITET, A.; STANLEY, K.; WALKER, D. & WHALEY, R.C. ScaLAPACK: A portable linear algebra library for distributed memory computers - Design issues and performance: Applied Parallel Computing Computations in Physics, Chemistry and Engineering Science Springer, 1996, p. 95-106.

DALQUEN, D.A.; ANISIMOVA, M.; GONNET, G.H. & DESSIMOZ, C. ALF - a simulation framework for genome evolution. Molecular biology and evolution, 2012, 29 (4): p. 1115-1123.

DEL TORO, L.; ROOSE, D. & GÁLVEZ, D. Construcción de árboles filogenéticos usando un método de mínima evolución basado en el método de los mínimos cuadrados (LS). En: Compumat 2011. Memorias del XII Congreso de la Sociedad Cubana de Computación y Matemática. Universidad Central "Marta Abreu" de las Villas: Editorial Feijóo, 2011, p. 10.

DESPER, R. & GASCUEL, O. Fast and accurate phylogeny reconstruction algorithms based on the minimum-evolution principle. Journal of computational biology, 2002, 9 (5): p. 687-705.

ELMROTH, E. & GUSTAVSON, F. A Faster and Simpler Recursive Algorithm for the LAPACK Routine DGELS. BIT Numerical Mathematics, 2001, 41 (5): p. 936-949.

FELSENSTEIN, J. Evolutionary trees from DNA sequences: a maximum likelihood approach. Journal of molecular evolution, 1981, 17 (6): p. 368-376.

FITCH, W. M. Toward defining the course of evolution: minimum change for a specific tree topology. Systematic Biology, 1971, 20 (4): p. 406-416.

GOUGH, B. GNU scientific library reference manual, Network Theory Ltd., 2009. 592 pp.

HARTIGAN, J.A. Minimum mutation fits to a given tree. Biometrics, 1973, 29: p. 53-65.

KHAN, S.U.; WANG, L. & ZOMAYA, A.Y. Scalable Computing and Communications: Theory and Practice, John Wiley & Sons, 2013. 856 pp.

KUMAR, S.; NEI, M.; DUDLEY, J. & TAMURA, K. MEGA: a biologist-centric software for evolutionary analysis of DNA and protein sequences. Briefings in bioinformatics, 2008, 9 (4): p. 299-306.

KURZAK, J. & DONGARRA, J. QR factorization for the Cell Broadband Engine. Scientific Programming, 2009, 17 (1): p. 31-42.

LETUNIC, I. & BORK, P. Interactive Tree Of Life v2: online annotation and display of phylogenetic trees made easy. Nucleic acids research, 2011: p. gkr201.

MARTHI, V.R. & CHENGALUR, J. Non-linear redundancy calibration. Monthly Notices of the Royal Astronomical Society, 2014, 437 (1): p. 524-531.

MAU, B. & NEWTON, M.A. Phylogenetic inference for binary data on dendograms using Markov chain Monte Carlo. Journal of Computational and Graphical Statistics, 1997, 6 (1): p. 122-131.

ORDONEZ, C.; MOHANAM, N. & GARCIA-ALVARADO, C. PCA for large data sets with parallel data summarization. Distributed and Parallel Databases, 2014, 32 (3): p. 377-403.

POSADA, D. jModelTest: phylogenetic model averaging. Molecular biology and evolution, 2008, 25 (7): p. 1253-1256.

SAITOU, N. & NEI, M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Molecular biology and evolution, 1987, 4 (4): p. 406-425.

SÁNCHEZ, R. & GRAU, R. An algebraic hypothesis about the primeval genetic code architecture. Mathematical biosciences, 2009, 221 (1): p. 60-76.

SIEVERS, F.; WILM, A.; DINEEN, D.; GIBSON, T.J.; KARPLUS, K.; LI, W.; LOPEZ, R.; MCWILLIAM, H.; REMMERT, M. & SÖDING, J. Fast, scalable generation of high‐quality protein multiple sequence alignments using Clustal Omega. Molecular systems biology, 2011, 7 (1)

ŠIRCA, S. & HORVAT, M. Matrix Methods: Computational Methods for Physicists Springer, 2012, p. 109-157.

SOKAL, R.R. & SNEATH, P.H.A. Principles of Numerical Taxonomy, W. H. Freeman, 1963. 359 pp.

TAMURA, K. & NEI, M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Molecular biology and evolution, 1993, 10 (3): p. 512-526.

YANG, Z. Computational Molecular Evolution, OUP Oxford, 2006. 374 pp.

ZHANG, H.; GAO, S.; LERCHER, M.J.; HU, S. & CHEN, W.-H. EvolView, an online tool for visualizing, annotating and managing phylogenetic trees. Nucleic acids research, 2012, 40 (W1): p. W569-W572.

 

 

Recibido: 14/11/2014
Aceptado: 19/01/2015