UNA GENERALIZACIÓN DE LOS MODELOS AMMI BASADA EN EL ALGORITMO DE TUCKALS3 PARA EL ANÁLISIS DE COMPONENTES PRINCIPALES DE TRES MODOS

 

Dr.C. M. Varela ^I, e. mail: [e-mail]; Ms.C. J. G. Castillo^II, y Dra.C. Ana Estévez^III; Dr. J. L. Vicente^IV, Dra. Purificación Galindo^IV y Dr. A. Blázquez^IV



I Investigador Auxiliar del Departamento de Matemática Aplicada

II Investigador Agregado

III Investigadora Titular del Departamento de Genética y Mejoramiento Vegetal, Instituto Nacional de Ciencias Agrícolas (INCA), Gaveta Postal 1, San José de las Lajas, La Habana, Cuba, CP 32700

IV Profesores del Departamento de Estadística, Universidad de Salamanca, España.

 

 

---

ABSTRACT

The three-mode Principal Component Analysis (TUCKALS3 model) is used to study three-way structured data, specifically three-order interaction associated to a lineal model. The three-order interaction residuals are decomposed by means of multiplying three marker matrices associated to each source of variation analyzed, searching for the best reduced dimension approximation according to the least squared estimation. TUCKALS3 will be applied to the genotype-environment interaction analysis, in order to evaluate the behavior of ten potato varieties under Cuban conditions. The unstable performance of these varieties under such conditions was proved.

 

Key words: statistical methods, genotype environment interaction, models

---

RESUMEN

Se utiliza el Análisis de Componentes Principales de tres modos (modelo de TUCKALS3) para estudiar datos con estructura de tres vías, específicamente los residuales de interacción triple asociados a un modelo lineal. Los residuales de interacción de tercer orden se descomponen a partir del producto de tres matrices de marcadores asociados a cada fuente de variación analizada, buscando la mejor aproximación en dimensión reducida en el sentido de los mínimos cuadrados. TUCKALS3 será aplicado en el análisis de la interacción genotipo-ambiente, con el objetivo de estudiar el comportamiento en las condiciones de Cuba de 10 variedades de papa establecidas en sus países de origen. Se pudo constatar el comportamiento inestable de las variedades en tales condiciones.

 

Palabras clave: métodos estadísticos, interacción genotipo ambiente, modelos

 

 

---

 

 

INTRODUCCIÓN

Los modelos AMMI (efecto de interacción multiplicativo y efectos principales aditivos) fueron propuestos para el análisis de la interacción de segundo orden asociado a un modelo lineal (1), específicamente para el de la interacción genotipo-ambiente. Estos modelos combinan las técnicas de Análisis de Varianza y Análisis de Componentes Principales; se basan en la descomposición en valores y vectores singulares de la matriz de residuales de interacción (2).
En estos modelos la interacción de segundo orden se descompone a partir de términos multiplicativos, lo que permite una representación grafica (Biplot) de los niveles de cada factor. Este tipo de representaciones simultáneas (3) ayuda a identificar las combinaciones de niveles causantes de la interacción.
Cuando se introduce un nuevo factor en el estudio, se incorpora al modelo de análisis de varianza un término de interacción triple; en tal caso, los estimadores correspondientes quedan incluidos en K matrices de orden IxJ, siendo I, J y K la cantidad de categorías de cada factor analizado. Integrar toda esta información es equivalente a hacer una generalización de las técnicas de reducción de dimensionalidad, en particular del Análisis de Componentes Principales para el caso de varias matrices de datos.
Para el análisis de datos con estructura de tres vías, es decir, de datos clasificados según las categorías de tres modos, se propone en 1966 el modelo de Tucker (4). Posteriormente se da un algoritmo (TUCKALS3), que se basa en encontrar los estimadores para A, B y C del modelo de Tucker, de manera tal que se minimice la suma de cuadrados residual (5). Este modelo ha sido aplicado en el análisis de la interacción genotipo ambiente (6, 7, 8).
En el presente trabajo se aplica el algoritmo de TUCKALS3 a los residuales de interacción de tercer orden, asociado a un modelo lineal con tres factores de variación, con el objetivo de estudiar, en las condiciones de Cuba, el comportamiento de 10 variedades de papa establecidas en sus países de origen.

 

MATERIALES Y METODOS

Se aplicó el algoritmo de TUCKALS3 para estudiar la interacción genotipo ambiente, en el caso en que los ambientes involucran dos factores de variación (localidades y años).
Específicamente se evalúa el rendimiento (t/ha) de 10 variedades de papa en tres localidades durante tres años. Las dos primeras localidades, Boyeros y San José de las Lajas, están ubicadas en la parte occidental de Cuba, mientras que la localidad de Villa Clara pertenece a la parte central del país. Son regiones de gran producción del tubérculo con condiciones climáticas extremas.
Las variedades estudiadas fueron: Aranka, Binella, Provento, Raja, Impala, Snowden, Granada, Desiree, Red Pontiac y Baraka. Se quiere estudiar el comportamiento en las condiciones de Cuba de estas 10 variedades ya establecidas en sus países de origen. Las variedades Snowden y Red-Pontiac son de procedencia canadiense, mientras que el resto son holandesas.
Modelo de TUCKALS3. Para el análisis de datos con estructura de tres vías, se propone el siguiente modelo (4):

donde A, B y C representan las matrices de marcadores asociadas a cada modo, en nuestro caso a cada factor de variación; P1, Q1 y R1 representan el número de componentes principales que se consideran en cada modo respectivo, mientras que G representa un arreglo de tres vías, cuyos elementos indican la relación existente entre las componentes de cada modo; así, el elemento gpqr indica la fuerza de la relación entre la componente p del primer modo, la componente q del segundo modo y la componente r del tercer modo. De igual forma, el valor (gpqr)2 representa la importancia de esta combinación de componentes en la inercia total explicada por el análisis. El arreglo de tres vías G puede ser considerado como una generalización de la matriz diagonal de valores propios asociada a la descomposición de dos vías.
Una solución para las matrices A, B y C del modelo ya fue dada (4); sin embargo, en ese trabajo se plantea que las soluciones encontradas no son estimadores mínimos cuadráticos, es decir, a pesar de que para el rango completo (P1= cantidad de componentes subyacentes en el primer modo, Q1= cantidad de componentes subyacentes en el segundo modo y R1= cantidad de componentes subyacentes en el tercer modo) se logra reproducir el valor zijk, al retener las primeras componentes de cada modo, el ajuste producido por el modelo puede ser lo suficientemente distante del verdadero valor de zijk como para ser considerado un mal ajuste.
Para tratar de resolver esta situación se propone un algoritmo (TUCKALS3), que toma como solución inicial la dada por Tucker y se basa en encontrar los estimadores para A, B y C, de forma tal que se minimice la suma de cuadrados residual (5):

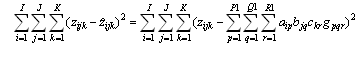
Aplicando el algoritmo de TUCKALS3 a los residuales de interacción de tercer orden asociado a un modelo lineal, se obtiene el siguiente modelo para un análisis de varianza con tres factores de variación:

Este modelo puede considerarse una generalización de los modelos AMMI para el caso de tres factores de variación. Para ajustar el modelo de TUCKALS3, es necesario fijar a priori el número de componentes a retener en cada modo, es decir, los valores de P1, Q1 y R1. En este trabajo se usa un algoritmo propuesto para encontrar el número de componentes a retener en cada modo (9). Este método asegura que la solución encontrada sea la óptima, en el sentido de buscar un compromiso entre la bondad de ajuste y el número de componentes principales.

 

RESULTADOS y DISCUSIÓN

En la Tabla I se ofrecen los valores medio para el rendimiento en cada una de las localidades y campañas analizadas.
En la Tabla II se representan los residuales de interacción triple asociados a las combinaciones de niveles de cada factor (variedades, localidades, años)
En la Tabla III se ofrecen las matrices de marcadores asociadas a cada factor de variación; se representa en cada caso la solución correspondiente a las dos primeras componentes de cada modo. La solución 2x2x2 fue la óptima encontrada. Esta solución explicó el 90.43 % de la variabilidad total asociada a los datos (bondad de ajuste):

En dicha tabla se muestra además el arreglo de tres vías G. La matriz contiene las relaciones entre los factores o componentes de cada modo; así, por ejemplo, el valor indica que el primer eje del modo i, el segundo eje del modo j y el primer eje del modo k absorben en su conjunto esa cantidad de inercia.
Con el ajuste del modelo de TUCKALS3 a los residuales de interacción triple, se respeta la verdadera estructura de tres vías presente en los datos (8, 10). Al no colapsar localidades y años, no se enmascaran los residuales de interacción de orden tres; estos quedan reflejados en su totalidad en la Figura 1.
En la Figura 1 se destacan como más inestables las variedades 1, 4, 5, 6, 7 y 9, por ser las más distantes al origen de coordenadas.
Variedad 1 (Aranka): Reacciona favorablemente en los ambientes L1A3 y L2A1, es decir, en la localidad Boyeros para el año 1993/1994 y en la localidad de San José de las Lajas para el año 1993/1994. Por otra parte, reacciona desfavorablemente en L1A2, es decir, en Boyeros para el año 1994/1995.
Variedad 5 (Impala): Reacciona favorablemente en L3A3 y L1A2, es decir, en Villa Clara para el año 1995/1996 y en Boyeros para el año 1994/1995. Tiene un comportamiento desfavorable en L1A3, o sea, en Boyeros para el año 1995/1996.
Variedades 4 y 9 (Raja y Red Pontiac): Reaccionaron favorablemente en Villa Clara y San José de las Lajas en la campaña 1995/1996 y en Boyeros para la campaña 1994/1995; sin embargo, tuvieron un comportamiento negativo en Boyeros para el año 1995/1996.
Variedad 6 (Snowden): Presenta altos rendimientos en las condiciones L2A3, es decir, en San José de las Lajas en el año 1995/1996 y mal comportamiento en L2A1, o sea, en Boyeros en el año 1993/1994.
Variedad 7 (Granada): Tuvo una interacción positiva en la localidad Boyeros para el año 1995/1996 y una interacción negativa en esta misma localidad para el año 1994/1995.
En sentido general, todas las variedades tuvieron un comportamiento bastante inestable.

 

CONCLUSIONES

La descomposición en valores y vectores singulares de los residuales de interacción de segundo orden, puede ser generalizada al caso de tres modos a partir del ajuste del modelo de Tucker a los residuales de interacción triple.
Los residuales de interacción de tercer orden pueden ser representados en dimensión reducida mediante un Biplot interactivo, concatenando dos de los modos.
Como consecuencia, los modelos AMMI pueden ser generalizados al caso de tres modos, resultado que permite realizar estudios de análisis de interacción genotipo ambiente, cuando los ambientes involucran dos factores de variación.
El método fue eficiente para estudiar la estabilidad de las variedades de papa probadas en diferentes localidades durante varios años. Se obtuvo una clasificación de las variedades en estables e inestables a partir de su interacción con el ambiente.

 

REFERENCIAS

1. Gauch, H. G. Model selection and validation for yield trials with interaction. Biometrics, 1988, vol. 44, p. 705-715.
2. Gollob, H. F. A statistical model which combines features of analytic factor and analysis of variance techniques. Psychometrika, 1968, vol. 33, p. 73-115.
3. Gabriel, K. R. The Biplot graphic display of matrices with applications to principal components analysis. Biometrika, 1971, vol. 58(3), p. 453-467.
4. Tucker, L. R. Some mathematical notes on three-mode factor analysis. Psychometrika, 1966, vol., 3, p. 279-311.
5. Hroonenberg, P. M. y De Leeuw, J. Principal Component Analysis of three-mode data by means of alternating least squares algorithms. Psychometrika, 1980, vol. 45, p. 69-77.
6. VanN Eeuwijk, F. A. y Kroonenberg, P. M. Multiplicative models for interaction in three-way ANOVA with Applications to Plant Breeding. Biometrics, 1998, vol. 54, p. 1315-1333.
7. Varela, M. Los métodos Biplot como herramienta de análisis de interacción de orden superior asociada a un modelo lineal (Tesis Doctoral) Universidad de Salamanca, España. 2002.
8. Varela, M.; Crossa, J.; Rane, J.; Kumar, A. y Trethowan, R. Analysis of a three-way interaction including multi-attributes. Australian Journal of Agricultural Research, 2006, vol. 57, no. 11, p.1185-1193.
9. Timmerman, M. E. y Kiers, H. A. L. Three-mode Principal Components Analysis. Choosing the numbers of components and sensitivity to local optima. British Journal of Mathematical and Statistical Psychology, 2000, vol. 53, p.1-16.
10. Varela, M. y Torres, V. Aplicación del Análisis de Componentes Principales de Tres Modos en la caracterización multivariada de somaclones de King grass. Revista Cubana de Ciencia Agrícola, 2005, vol. 39, p. 12-19.

Recibido: 24 de octubre de 2007
Aceptado: 5 de mayo de 2008