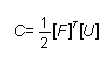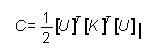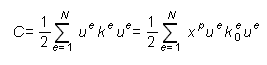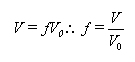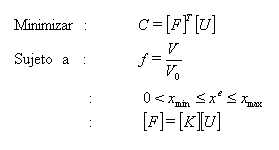ARTÍCULOS ORIGINALES

 

Predicción del proceso de remodelación ósea para diferentes implantes de cadera al utilizar optimización topológica

 

Prediction of the bone remodeling process for different hip implants using topological optimization

 

 

Diego Alexander Garzón-Alvarado^I; Máximo Alejandro Roa Garzón^II; Angélica María Ramírez Martínez^III

^I Doctor en Ciencias. Profesor Asociado. Grupo de Modelado y Métodos Numéricos en Ingeniería. Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia, Bogotá, Colombia.
^II Doctor en Ciencias. Investigador del Instituto de Organización y Control de Sistemas Industriales. Universidad Politécnica de Cataluña. Profesor Asociado. Universidad Nacional de Colombia.
^III Doctora en Ciencias. Investigadora Grupo de Estructuras y Modelado de Materiales. Universidad de Zaragoza, Zaragoza, España. Profesora Fundación Universidad Central.

 

 

---

RESUMEN

Se propone utilizar la optimización topológica para la evaluación de implantes totales de cadera. Para esto se comparan dos tipos de endoprótesis: tipo Lazcano, cuyo componente intrafemoral (tallo) es curvado y, de tallo recto. A partir de la evaluación de estos dos componentes, se compara la reabsorción ósea y la distribución de densidad del tejido pos implante, lo cual permite un diagnóstico preliminar del hueso, del componente intrafemoral y la elección del implante apropiado. Para efectuar esta comparación se realiza una simulación en dos dimensiones al usar una optimización topológica con el método de elementos finitos, lo que constituye un primer acercamiento al problema de la evaluación del tipo de prótesis a utilizar y del comportamiento del tejido óseo tras el implante de cadera. Los resultados de este procedimiento numérico permiten estimar el estado final de la densidad ósea del hueso, después del implante de cadera que es comparable con los patrones obtenidos en la práctica clínica. Con este proceso se puede determinar una mejor geometría del implante para evitar una pérdida excesiva de masa ósea.

Palabras clave: Remodelación ósea, métodos numéricos, optimización topológica, elementos finitos, biomecánica, evaluación de la prótesis.

---

ABSTRACT

The use of topology optimization for the evaluation of total hip implants was presented. To this end, two types of endoprostheses were compared, that is, the Lazcano type, the intrafemoral component (stem) of which is curved, and the straight stem. Based on the evaluation of these two components, bone re-absorption and tissue density distribution after implantation was compared, allowing preliminary intrafemoral bone and intrafemoral component diagnosis, and the selection of appropriate implant. In order to make his comparison, a two-dimensional simulation using topological optimization under the finite element method was performed, which is a first approach to the problem of evaluating the type of prosthesis to be used and the behavior of bone tissue after hip implant. The results of this numerical procedure lead to an estimation of the final bone density after hip implant that is comparable with the clinical practice patterns. This process can better determine the best implant geometry, thus avoiding excessive bone mass loss.

Key words: bone remodeling, numerical methods, topology optimization, finite elements method, biomechanics, prosthesis evaluation.

---

Évaluation prédictive par optimisation topologique du processus de remodelage des différents implants de hanche

RÉSUMÉ

Dans ce travail, l'utilisation de l'optimisation topologique est proposée pour l'évaluation des implants totaux de hanche. Deux types d'endoprothèse sont donc comparées: l'endoprothèse Lazcano, dont la tige fémorale est courbée, et l'endoprothèse à tige droite. À partir de ces deux éléments, la résorption osseuse et la distribution de la densité tissulaire après un implant sont mises en considération, ce qui permet une analyse préliminaire de l'os, de la tige fémorale et de la sélection de l'implant approprié. Afin de réaliser cette analyse, une simulation en 2D est effectuée en utilisant l'optimisation topologique sous forme d'éléments finis, ce qui constitue la première approche du problème d'évaluation de la prothèse à utiliser et du comportement du tissu osseux après un implant de hanche. Les résultats de cette technique numérique, étant comparables aux standards obtenus dans la pratique clinique, permettent d'estimer l'état final de la densité osseuse après un implant de hanche. Grâce à cette méthode, une meilleure géométrie de l'implant peut être déterminée pour éviter une perte excessive de masse osseuse.

Mots-clés: Remodelage, méthodes numériques, optimisation topologique, éléments finis, biomécanique, évaluation de la prothèse.

---

 

 

INTRODUCCIÓN

La artrosis de la cadera afecta habitualmente a personas de mediana y avanzada edad.¹ Los síntomas van desde unas leves molestias hasta un dolor severo incapacitante.² El tratamiento de la artrosis de la cadera busca la disminución del dolor y la mejora de la movilidad de la articulación.

El cirujano ortopédico con su experiencia en problemas óseos y articulares debe evaluar las condiciones para una eventual sustitución protésica. Si el estudio radiográfico³ muestra un daño articular severo y ninguna otra forma de tratamiento se ha conseguido un alivio satisfactorio. El cirujano ortopédico puede sugerir la sustitución articular.

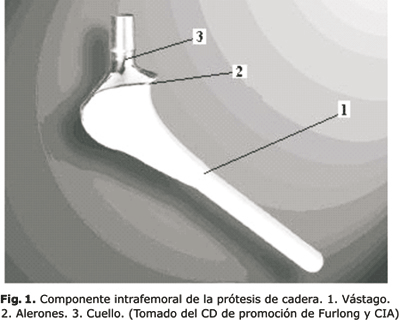
La prótesis total de cadera consiste en reemplazar las dos partes que conforman la articulación. Por un lado, el acetábulo que corresponde a la parte de la pelvis de la cadera y por otro, la cabeza del fémur (figs. 1, 2 y 3). Existen múltiples tipos de prótesis de cadera⁴ con el avance de la tecnología se han podido desarrollar nuevos dispositivos con materiales más resistentes.⁴ Actualmente la duración de una prótesis total de la cadera es aproximadamente de 15 años.¹

La selección del tipo de prótesis debe responder a las necesidades personalizadas de los pacientes.⁴ En términos generales se puede resumir de la siguiente forma:

1. En pacientes jóvenes menores de 65-70 años se recomienda la utilización de prótesis no cementadas de titanio. Las ventajas de este tipo de prótesis son que permiten que el hueso del paciente crezca y se adhiera a la prótesis y posibilitan una fijación duradera. Además, la nueva tecnología permite que en caso de desgaste de la prótesis, se puedan cambiar los elementos desgastados y no tener que sacar la prótesis completa.

2. En pacientes mayores de 70 años se recomienda la utilización de prótesis que se fijan al hueso con cemento.

La sustitución total de cadera genera anualmente más de 300 000 operaciones en el mundo.¹ La historia de este procedimiento cita a Philip Wiles quien en 1938 realizó en Londres una artroplastia de cadera con acero inoxidable. En 1943 Moore y Bohlman¹ publican un caso de prótesis endofemoral en una paciente con tumor de células gigantes. Sir. John Charnley en los años sesenta introdujo el cemento PMMA (Polimetíl metacrilato) con lo que obtiene buenos resultados en cuanto al aflojamiento de la prótesis.²

Ya en los años sesenta se popularizó la cirugía del implante de cadera y se introdujeron modelos como el de vástago de Müller que es basado en los diseños de Charnley.¹

La medicina ortopédica actual se encuentra en la búsqueda del comportamiento del tejido óseo ante las cargas impuestas a diferentes tipos de huesos, especialmente al fémur.⁵ Por ello, este trabajo muestra el análisis por optimización topológica para conocer la respuesta en la composición de la densidad del tejido óseo del fémur después de la artroplastia de cadera. Desde el punto de vista de optimización topológica, y tal como lo afirmó Roux y Wolf¹, el tejido óseo sigue un proceso de adaptación a los procesos de carga y descarga propios de la actividad física. En este artículo se presenta una metodología para el modelado matemático y el análisis numérico de la distribución de densidad del tejido tras el implante total de cadera, lo cual permitirá evaluar la efectividad de la geometría de las prótesis.

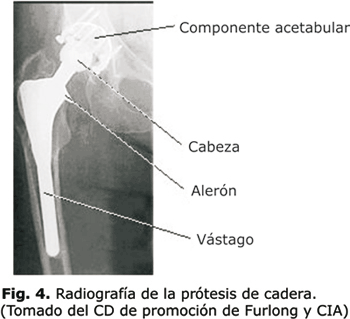
En primera instancia, en este artículo se presenta en forma breve, la teoría de optimización topológica basada en el método de los elementos finitos. Posteriormente, se enseña la metodología utilizada para obtener la geometría de la prótesis y del fémur humano a partir de las tomografías axiales computarizadas y el trabajo sobre software especializado. Luego se llevan a cabo las simulaciones del fémur con la endoprótesis para obtener los resultados que son discutidos y que dan paso, por último, a las conclusiones (fig. 4).

Optimización topológica: teoría matemática

El objetivo fundamental de la optimización topológica es encontrar la distribución de masa en una estructura que esta sometida a condiciones de carga y restricciones de frontera específicas, de tal forma que cumpla con una función objetivo que se debe optimizar.⁶

La cantidad de material y su distribución está limitada en el dominio del diseño: Ù. El dominio mencionado, puede contener regiones con material, o con vacíos que no pertenecen al análisis, y por tanto, se denominan regiones pasivas. A diferencia del dominio pasivo, el dominio activo debe ser optimizado bajo una función (objetivo).

La solución del problema de la optimización se lleva a cabo mediante el método de los elementos finitos (fig. 5).

En este método se requiere hallar la solución a problemas de valor en la frontera con condiciones iniciales y asumir que el dominio se divide en subdominios, los cuales se denominan elementos, y que la función desconocida de una variable de estado se define en forma aproximada en cada uno de los elementos.⁷ Con estas funciones que son definidas individualmente para cada elemento y en conjunto, con los demás subdominios unidos a través de nodos (los cuales se encuentran en la interfaz de los elementos), se aproxima la solución sobre del problema.

Gracias a que el dominio completo se divide en numerosos elementos y la función objetivo (solución) es aproximada en ciertos puntos, llamados nodos, es imperativo la solución de un sistema con un gran número de ecuaciones.^6,7

Al considerar las ecuaciones básicas de esfuerzo-deformación^8-10 el cálculo de deflexiones de cada elemento producidas por el sistema de carga son transmitidas desde los elementos vecinos a través de los puntos nodales. Por ello, la deformación se determina a partir de los puntos nodales, así mismo los esfuerzos se calculan a partir de la deflexión tomando en cuenta la ecuación constitutiva adecuada.¹⁰

El paquete de información más pequeño en el análisis por elementos finitos, es la llamada matriz de rigidez para cada elemento, cuya expresión se obtiene a partir de la formulación seleccionada. La matriz de rigidez se puede conceptuar como una "pseudo" constante de resorte que describe (en el caso mecánico) el desplazamiento de puntos nodales bajo la acción del sistema de fuerzas (o cargas en general). En notación matricial se expresa (1):

[¦]^e = [k]^e [u]^e

Con e= 1 hasta N (donde N es el número total de elementos finitos en el dominio). Donde [¦]^e es el vector columna de fuerza actuante sobre el elemento (o cargas actuantes sobre el sistema, ya sean térmicas, eléctricas etc.), [k]^e es la matriz de rigidez del elemento (en la cual se consideran las propiedades físicas, en este caso elásticas.^8-10 [u]^e es la matriz de desplazamiento (o cualquier otra variable de estado). Cuando se ensamblan los paquetes de información de cada uno de los elementos para configurar el sistema, se obtiene la ecuación matricial (2):

[F]= [K] [U]

Donde: [K]: Matriz de rigidez maestra (o global), la cual es ensamblada a partir de [k]^e para los elementos. [F]: Fuerzas externas a cada nodo, [U]: desplazamientos de los nodos. Las incógnitas son los desplazamientos o variables de estado. Estas ecuaciones son resueltas computacionalmente, y se obtienen los desplazamientos de los puntos nodales, para posteriormente emplear esta solución en el cálculo de otras variables, como por ejemplo, los esfuerzos, para más detalles remítase a.¹⁰

Minimización de una variable con restricciones

Para llevar a cabo el proceso de optimización topológica (o de forma) se define la variable de diseño x^e que representa la densidad relativa del material en el elemento e, esto es (3)⁶:

r^e= x^e r0

Donde: r0: Es la densidad del elemento en el dominio de diseño sin optimizar. Gracias a esta variable, la elasticidad y, por tanto, la resistencia de un modelo estructural modifican su comportamiento ante cargas externas hasta llegar a su estado óptimo. Es así, como la matriz de rigidez para un elemento e se convierte en (4):

k^e= (x^e)^p k0

Donde k0: es la rigidez inicial y p es el factor de penalización.⁶ Si p= 1, la experiencia indica⁶ que el mapa de las densidades puede obtener valores intermedios. Si p= 3, el material se optimiza hasta encontrar distribuciones de densidad que toman valores relativos de 0 o 1.

Se desea entonces minimizar la densidad de energía de deformación existente en el componente estructural al homogenizar su valor en todo el continuo del modelo. Para ello, se utiliza el concepto de la energía almacenada en un resorte:

Energía almacenada en un resorte

De forma análoga, la energía almacenada en un dominio continuo por la acción de fuerzas externas se puede expresar como (5):

Al reemplazar el vector [F] de (2) se obtiene (6):

Al continuar reemplazando la ecuación (4) en (6) y realizando la notación en términos del desplazamiento y rigidez de los elementos se obtiene (7):

Donde N: es el número de elementos del dominio continuo. C es la función objetivo del problema de optimización.

Por otro lado, el volumen del material que se desea remover por optimización está dado por (8):

Donde: ¦ es la fracción del material que se desea remover y V₀ es el volumen total del dominio del diseño en su estado no optimizado (volumen inicial).

Definidas las anteriores variables, el proceso de optimización se reduce matemáticamente al siguiente problema: 1. minimizar la energía de deformación sujeto a 2. Modificar el estado actual de la densidad del dominio para disminuir la densidad del tejido que se encuentra en bajas condiciones de carga y aumentar la densidad en aquellos sitios que tienen alta solicitación mecánica. Este problema se puede escribir matemáticamente como (9):

Donde x_min y x_max: son los límites superior e inferior de la densidad relativa respectivamente.

Se puede escoger por ejemplo, x_max= 1 y x_min= 0,3 > 0 de tal suerte que se evite que la matriz de rigidez se convierta en singular.⁶

En muchos ejemplos prácticos,⁶ la reducción del volumen en el dominio de diseño puede ser f= 0,5 (50 % de reducción), se debe tener en cuenta que 0 < f= 1.

En este momento cabe la pregunta: ¿Cuáles son los métodos de solución? Existen varios métodos para solucionar el problema de optimización con lo cual se desea hallar x^e. El primer método esta basado en la formulación lagrangiana, donde se utiliza un criterio de optimalidad (método heurístico) para actualizar las variables de diseño y los multiplicadores de Lagrange encontrados en cada iteración.⁶

En el caso del problema de optimización topológica aplicado a la biomecánica del implante de cadera, se requiere minimizar la masa (o el volumen) del hueso ósea sujeto a ciertas condiciones de carga, en este caso, condiciones de carga en la cabeza femoral y en el trocanter mayor.

 

MÉTODOS

A continuación, se propone utilizar la optimización topológica en la evaluación de implantes totales de cadera. Para ello, se comparan dos tipos de endoprótesis:

1. Tipo Lazcano⁵ cuyo componente intrafemoral (tallo) es curvo.

2. De tallo recto,⁵ en la cual su componente intrafemoral es recto.

A partir de la evaluación de estos dos componentes, se compara la reabsorción ósea que toma lugar posimplante, lo cual colabora en el diagnóstico del hueso del componente intrafemoral y en la escogida del implante apropiado.

Inicialmente se realiza la simulación en dos dimensiones, lo que constituye una "primera aproximación" al problema de la evaluación del tipo de prótesis a utilizar y al comportamiento del fémur (en cuanto a su mapa de densidades objetivo: posoperación). En un siguiente artículo se llevará a cabo la simulación tridimensional del componente intrafemoral.

Prótesis

Se evalúan dos prótesis: de tallo recto y tipo Lazcano. Las prótesis se realizan en un modelador tridimensional, en éste caso SOLID EDGE. Mediante el software CAD, paramétrico tridimensional, se obtienen los detalles intrincados de las prótesis para su uso tridimensional, o bidimensional según sea el caso.

A. De tallo recto: En la figura 6 se muestra la prótesis de tallo recto realizada en el modelador tridimensional.

Como se observa, la prótesis de la figura 6 presenta su tallo recto, el cual debe quedar al interior de la médula del fémur. El componente posee dos agujeros (lateral y en dirección del eje de la prótesis) que son utilizados para el crecimiento y anclaje óseo. En dichos agujeros se inicia el proceso de la decantación ósea que ayuda a la fijación del componente. Obsérvese también, el collar femoral, el cual es una ayuda eficaz para la distribución de la presión en el fémur para evitar la llamada pérdida calcar ósea.

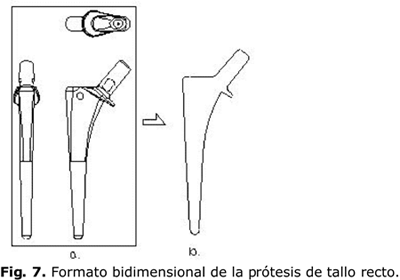
Para la utilización de dicho componente en análisis bidimensional, se obtienen las vistas de las prótesis, como se observa en la figura 7, mediante la utilización del subpaquete de Solid Edge para la realización de planos a partir de la figura tridimensional.

Por último, para simplificar la geometría que es utilizada en la simulación mediante elementos finitos con ANSYS, se llevan las vistas bidimensionales a formato CAD 2D, es decir, se lleva a formato*.dwg, propio de AUTOCAD. En este formato (en el cual es factible modificar la geometría) se dibuja el contorno de la prótesis para llevarla posteriormente a ANSYS.

La geometría final para el análisis se muestra en la figura 7b. Este contorno está en contacto con el interior del agujero del fémur donde va alojada la prótesis.

B. Tipo Lazcano: De igual forma, la prótesis tipo Lazcano (o de tallo curvado) se muestra en la figura 8.

Obsérvese que este tipo de prótesis (fig. 8) es curva en su componente intrafemoral, lo cual evita concentraciones de esfuerzo en el fémur y en la prótesis. También se presenta un collar (más pronunciado que el de la prótesis de tallo recto) para la transferencia de carga. Se observa además, que el tallo tiene menor espesor en la parte superior.

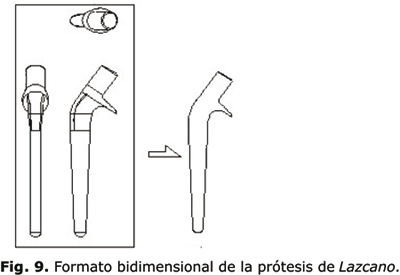
Al seguir un procedimiento similar al enunciado en la prótesis de tallo recto, se obtienen las vistas y el contorno de la prótesis tipo Lazcano como se observa en la figura 9.

Fémur

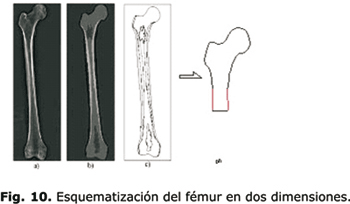
El fémur es dibujado en dos dimensiones a partir de las tomografías axiales computarizadas. En este caso, se parte de un formato* bmp (que entrega el tomógrafo), se delimita el contorno al utilizar COREL TRACE (de COREL DRAW) y por último, se obtiene el contorno en AUTOCAD, como se observa en la figura 10.

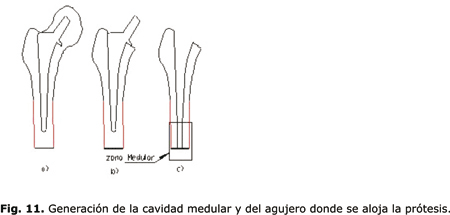
Para llevar a cabo la geometría del agujero donde va alojada la prótesis se coloca tanto el fémur proximal como la prótesis en escala de 1:1, con lo cual se obtiene el contorno del sitio donde debe ir el corte de la cabeza femoral, como se observa en la figura 11.

La figura 11a) muestra el fémur con la prótesis de tallo recto en escala 1:1. La figura 11b) muestra el corte realizado a la cabeza femoral. Por último, la figura 11c) muestra el fémur con el agujero central donde va alojado la endoprótesis. De forma similar se realiza el análisis para la prótesis tipo Lazcano.

Implementación de cargas

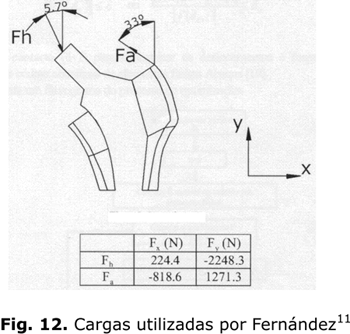
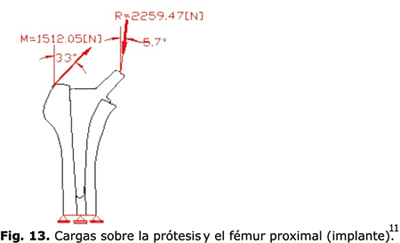
La aplicación adecuada de cargas y de restricciones es imprescindible en el modelo para obtener datos cercanos a la realidad. Fernández y Rubén¹¹ reportan cargas promedio sobre el fémur de una persona (de 80 kg de peso) en marcha fisiológica como las observadas en las figuras 12 y 13.

De este modelo de cargas se pueden deducir los siguientes valores expresados en la tabla 1.

Materiales utilizados

Actualmente se acepta la microscopia acústica como la técnica más recomendada para obtener los datos elásticos del material (hueso).¹² Además, se ha determinado que las propiedades del hueso trabecular y el cortical son similares a nivel microscópico.¹³ Como primera aproximación en este trabajo se suponen valores similares para ambos tipos de tejidos. Gracias a la técnica de microscopia acústica se toman como datos del fémur proximal las siguientes propiedades expuestas en la tabla 2.

Obsérvese que la diferencia existente entre el módulo de elasticidad del tejido esponjoso y el cortical es menor a 1,3 % a nivel microscópico.^12,13 Mediante una simplificación y como primera aproximación en este trabajo se utiliza para el hueso cortical y esponjoso un módulo de elasticidad de E= 17,6 GPa. El módulo de Poisson a utilizar es 0,365.

Materiales para la prótesis

Las prótesis se suponen construidas en la aleación Ti-6Al-4V, por ser una de las más empleadas gracias a su biocompatibilidad y biocompetencia.¹ Estas prótesis también son hechas en aceros inoxidables de extra bajo contenido de carbono (menor al 0,2 %) denominados aceros: 314L y 316L.^1,14

En Colombia se utilizan ampliamente aceros inoxidables 316L cuyo módulo de elasticidad es 200 GPa y con un módulo de Poisson de 0,26.⁹ Con estos datos se alimenta el programa de elementos finitos ANSYS para llevar a cabo la simulación.

SIMULACIÓN

El procedimiento para obtener el mapa de la densidad a partir de la simulación se describe en la figura 14.

Como se muestra en la figura 14, el proceso de solución del problema de contacto y optimización topológica requiere del acople de dos análisis independientes no lineales. Inicialmente se lleva a cabo el problema del contacto (el cual es no lineal), de donde se obtiene el mapa de esfuerzos, desplazamientos y de presiones de contacto entre el fémur y la prótesis. Con los datos antes obtenidos, se lleva a cabo el proceso de optimización topológica al utilizar las presiones de contacto como cargas en el proceso de optimización.

Simulación del comportamiento del tejido ante la prótesis de tallo recto completamente unida al hueso (análisis dual)

La cantidad de material y su distribución está limitada en el dominio del diseño: El dominio mencionado, puede contener regiones con material o con vacíos que no pertenecen al análisis, y por tanto, se denominan regiones pasivas (como se había mencionado en el apartado 2).

La simulación del análisis topológico de la prótesis completamente unida al fémur es un caso en el cual se divide el dominio en dos: pasivo y activo. El dominio pasivo esta representado por la prótesis, gracias a que esta no presenta cambios en su densidad (o regeneramiento) al tener solicitaciones mecánicas. El dominio activo, representado por el fémur, presenta cambios en la densidad (remodelado óseo) para maximizar sus condiciones mecánicas (uniformizar la energía y minimizar el volumen). En la figura 15 se observa la configuración del análisis.

Para la simulación de la prótesis de tallo recto se utilizan las cargas enunciadas por Fernández, el material femoral y el material de la prótesis entregado en anteriores apartes.

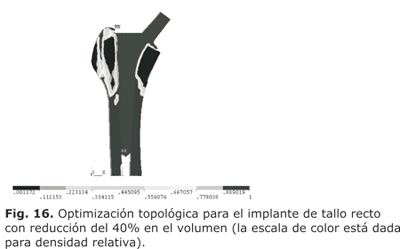
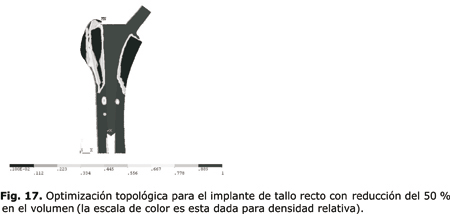
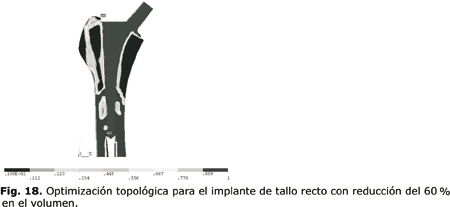
En la figura 16 se muestra la optimización topológica para el análisis de la prótesis de tallo recto (para el cual se llevó a cabo un análisis previo de convergencia, que no se muestra en este artículo). Para la optimización con reducción del 40 % se realizaron 10 iteraciones, para una reducción del 50 % se realizaron 11 iteraciones (fig. 17) y para un 60 %, 20 iteraciones (fig. 18). (La escala de color está dada para densidad relativa). La simulación se realizó en un Pentium IV, de 2 GHz, 512 MRam, y tiene una duración promedio de 5 h cada análisis.

En condiciones fisiológicas, al aplicar carga sobre el hueso esponjoso de la cabeza, existe una redistribución de esfuerzo distalmente hacia las corticales, lo que mantiene la remodelación ósea. La carga se transfiere por estructuras periféricas. Como se observa en la gráfica de densidad, la carga se transmite a través del vástago por el interior del espacio medular y pasa hasta llegar a la punta de la prótesis (en donde se observa la mayor densidad relativa), lo cual permite el mantenimiento del tejido cortical (en la zona distal medial y lateral), como se observa en el mapa de densidad. Sin embargo, la densidad relativa disminuye en comparación con el hueso fisiológico (sin implante), lo cual era de esperar en un procedimiento posoperatorio.

Se observa que en la parte diafisiaria, entre el endostio y el periostio, existe una remoción leve del tejido óseo. Sin embargo, desde que se mantengan las regiones externas del hueso, eventualmente se genera tejido gracias a que allí se encuentran los osteoblastos que pueden iniciar un proceso de reconstrucción ósea.¹²

Se observa que se la trabécula ósea que une el punto de inserción muscular y el tejido cortical se mantiene gracias a que en el análisis existe una transferencia total de carga.

Comparación con el análisis con superficie de contacto

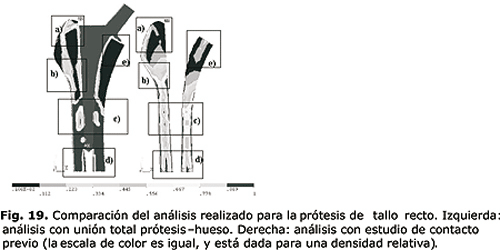
Se observa en la figura 19 la comparación entre la optimización topológica con estudio previo de contacto y la optimización topológica con dominios activo y pasivo, para una reducción en volumen del 60 porciento.

Como se observa en la figura 19 existen diferencias significativas entre los dos análisis. En primera instancia, lo cual es de esperar, el tejido cortical y trocantérico se conserva gracias a la eficiente transferencia de carga desde la prótesis hasta el fémur en condiciones de unión total, a diferencia de lo que ocurre cuando la prótesis no tiene unión efectiva.

Se observa también la conformación del tejido lateral externo en los dos casos de análisis. Sin embargo, en el análisis con contacto previo se observa una disminución de la densidad relativa por la pobre estimulación del tejido en esta zona, ejercida por el contacto con la prótesis.

En los cuadros b) de la figura 19, se observa que en el caso con contacto existe una distribución más uniforme de la densidad (y por ende de la masa), existe además, una gran similitud con el análisis de topología dual, gracias a que se conserva cualitativamente la forma de la trabécula en esta zona, la cual se conecta desde la zona de inserción muscular hasta el tejido cortical.

En los cuadros c) y d) se observa la conformación del tejido cortical. En el análisis topológico dual se muestra que el tejido cortical no presenta grandes pérdidas de masa ósea debido a la perfecta unión prótesis-hueso y a la transferencia de carga efectiva. A diferencia de este análisis, en el análisis con estudio previo de contacto se lleva a cabo una pérdida significativa de hueso en la región cortical y se conserva el periostio y el endostio.

El cuadro e) muestra la región proximal medial (también llamado calcar) en donde se observa una gran pérdida del tejido en el análisis topológico dual. Esto se debe a que existe una transferencia uniforme de carga a través de la interfaz hueso-prótesis (a lo largo de todo el fémur) la región calcar no recibe la solicitación de carga real existente, lo cual se traduce en pérdida de masa ósea. A diferencia de este análisis, el análisis con estudio de contacto previo permite observar la transferencia de carga en esta zona, con lo cual se obtiene una estimulación ósea y por tanto una cantidad de tejido en el área, es decir, no se reabsorbe totalmente el hueso en dicha región.

Para concluir, el análisis de prótesis al utilizar un estudio de contacto previo, revela una distribución de masa más cercana a la realidad que aquella que con el estudio topológico dual. La región calcar es un claro ejemplo de cómo el análisis topológico con dominios duales no representa la realidad, debido a que la transferencia de carga en este tipo de análisis es uniforme a lo largo del vástago. En este tipo de análisis no se tiene en cuenta las zonas de mayor presión de contacto, zonas donde se pierde el contacto de la interfaz y en aquellas regiones donde se presentan movimientos relativos.

Es indispensable para la evaluación de la prótesis llevar a cabo estudios de contacto, analizar experimentalmente los coeficientes de fricción en la interfaz y evaluar aquellos implantes que utilizan cemento para evitar la movilización de la prótesis (sea de cualquier articulación corporal).

Simulación del comportamiento del tejido de la prótesis de tallo curvo tipo Lazcano completamente unida al hueso (análisis dual)

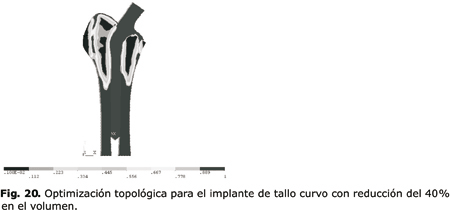
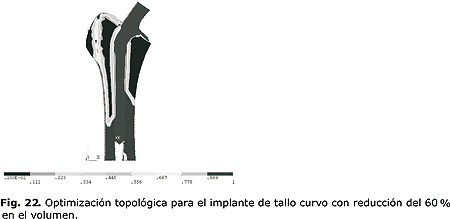
En las figuras 20 a la 22 se muestra la optimización topológica para el análisis de la prótesis de tallo curvo (la escala de color está dada para densidad relativa), para la cual se realizó un análisis previo de convergencia. Para la optimización con reducción del 40 % se llevaron a cabo 11 iteraciones (fig. 20), para una reducción del 50 % (fig. 21). Se realizaron 8 iteraciones y para un 60 %, 11 iteraciones (fig. 22). La simulación se realizó en un Pentium IV, de 2 GHz, 512 MRam, y tiene una duración promedio de 5 horas cada análisis.

A diferencia del análisis del implante con tallo recto con el análisis topológico dual, se observa en las figuras 20 y 21 el comportamiento del tejido ante la utilización del collar en la prótesis y se observó un estímulo que promueve la generación ósea en la zona calcar. En la figura 22 no se muestra la condición de regeneramiento calcar.

Se observa que en la parte diafisiaria, entre el endostio y el periostio, existe una remoción leve del tejido óseo. Sin embargo, desde que se mantengan las regiones externas del hueso, eventualmente se genera tejido gracias a que allí se encuentran los osteoblastos.

Se observa que se la trabécula ósea que une el punto de inserción muscular y el tejido cortical se mantiene porque en el análisis existe una transferencia total de carga.

El tejido cortical lateral se ve disminuido en comparación con el análisis realizado en la prótesis de tallo recto.

Comparación con el análisis con estudio de contacto previo

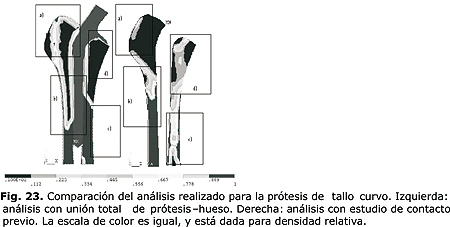
Se observa en la figura 23 la comparación entre la optimización topológica con estudio previo de contacto y la optimización topológica con dominios activo y pasivo, para una reducción en volumen de 60 por ciento.

Como se observa en la figura 23 existen diferencias significativas entre los dos análisis. En primera instancia, lo cual es de esperar, el tejido cortical y trocantérico se conserva gracias a la eficiente transferencia de carga desde la prótesis hasta el fémur en condiciones de unión total.

En el su cuadro a) de la figura 23 se observa la conformación del tejido lateral externo (trocantérico) en los dos casos de análisis. Sin embargo, en el análisis con contacto previo se observa una disminución de la densidad relativa por la pobre estimulación del tejido en esta zona ejercida por el contacto con la prótesis.

En los cuadros b) de la misma figura se observa que en el caso con contacto, existe una distribución más uniforme de la densidad (y por ende de la masa), existe además, una gran similitud con el análisis de la topología dual, lo cual se debe a que se conserva cualitativamente la forma de la trabécula en esta zona, la cual se conecta desde la zona de inserción muscular hasta el tejido cortical. Existen pérdidas menores en la cantidad de tejido (masa) en el análisis con estudio de contacto.

En los cuadros c) se observa la conformación del tejido cortical. En el análisis topológico dual se muestra que el tejido cortical no presenta pérdidas de masa ósea debido a la perfecta unión prótesis -hueso y a la transferencia de carga efectiva. A diferencia de este análisis, en el análisis con estudio previo de contacto se lleva a cabo una pérdida significativa de hueso en la región cortical y se conserva el periostio y el endostio.

El cuadro d) muestra la región proximal medial (también llamado calcar) en donde se observa una gran pérdida de tejido en el análisis topológico dual. Se debe a que existe una transferencia uniforme de carga a través de la interfaz hueso-prótesis (a lo largo de todo el fémur), la región calcar no recibe la solicitación de carga real existente, lo cual se traduce en pérdida de masa ósea. A diferencia de este análisis, el análisis con estudio de contacto previo, permite observar la transferencia de carga en esta zona, con lo cual se obtiene una estimulación ósea y por tanto, una cantidad de tejido en el área, es decir, no se reabsorbe totalmente el hueso en dicha región.

 

DISCUSIÓN

En el presente artículo se plantea un esquema de trabajo aplicado a la recuperación del tejido, selección de la prótesis y evaluación diagnóstica para aplicaciones clínicas. Desde esta perspectiva es importante notar que la optimización topológica permite predecir si el funcionamiento de un hueso está en rangos de normalidad, gracias a que el conjunto celular de osteoblastos, osteoclastos y osteocitos actúa como un sistema de detección y construcción mecánica como se ha demostrado en diversas investigaciones experimentales.¹²

Por tal razón, la optimización topológica se convierte en una poderosa herramienta de apoyo para ortopedistas y médicos en general con fines de evaluación ósea.

Con dicha metodología se ha hallado que la geometría de las prótesis incide en la transferencia de carga, lo cual es importante para su evaluación y la aplicación en pacientes particulares.

Por ejemplo, gracias a la acción del collar de la prótesis, se observa que la zona calcar (parte medial-proximal) no pierde tejido óseo en toda su extensión. Esto se debe a que allí existe una transferencia de carga adecuada que estimula las células mecanoreceptoras.

La presencia de un collar en la prótesis con el fin de obtener un apoyo directo sobre el cuello femoral para repartir los esfuerzos sobre el fémur evita la reabsorción del mal llamado "calcar".

En condiciones fisiológicas, al aplicar carga sobre el hueso esponjoso de la cabeza existe una redistribución del esfuerzo distalmente hacia las corticales, lo que mantiene la remodelación ósea. La carga se transfiere por estructuras periféricas. Como se observa en la gráfica de esfuerzos, la carga se trasmite a través del vástago por el interior del espacio medular pasando hasta llegar a la punta de la prótesis, lo cual permite el mantenimiento del tejido cortical (en la zona distal medial y lateral), como se observa en el mapa de densidad. Sin embargo, la densidad relativa disminuye en comparación con el hueso fisiológico (sin implante), lo cual era de esperar en un procedimiento posoperatorio.

Un contacto total cuello_collar evitará la reabsorción, sin embargo en la realidad se obtendrá contacto entre 1 o 2 áreas. Las zonas corticales (periostio y endostio) se mantienen inmodificadas en su zona distal, pero en la región trocantérica (lateral-proximal). Se reabsorbe el hueso por falta de contacto y transferencia de carga desde la prótesis al fémur.

Se observa que en la parte diafisiaria, entre el endostio y el periostio, existe una remoción importante del tejido óseo.

Los datos obtenidos en las gráficas arrojadas por ANSYS son de fácil interpretación. Cuando se habla de densidad relativa se observa cualitativamente aquellas zonas de mayor masa ósea. Es así como las gráficas "pueden" ser objeto de trabajo para médicos en pro del diagnóstico de enfermedades osteológicas.

Los modelos aquí desarrollados deben contrastar con lo obtenido en clínica. Sin embargo, el modelo bidimensional es una aproximación a las condiciones reales del fémur. Por ello se debe tener cuidado en la interpretación teniendo en cuenta que los valores pueden distar del comportamiento real. Las gráficas dadas aquí son cualitativas.

Agradecimientos

Este artículo es el resultado parcial del proyecto financiado por la División de Investigaciones de Bogotá, DIB, de la Universidad Nacional de Colombia, bajo el título: "Modelado matemático y simulación de procesos en Ingeniería Mecánica y Biomédica".

 

REFERENCIAS BIBLIOGRÁFICAS

1. Munuera L, García E. La prótesis total de cadera cementada. España: Interamericana-McGraw Hill. Madrid 1ra. ed; 1989.

2. Harris W, Sledge C. "Total hip an total knee replacement". E.U.A. The New England Journal of Medicine. 1990;323(11):725-731.

3. Weissman B, Sledge NW, Clement B. Orthopedic radiology. Estados Unidos: Saunders Company. W.B. Washington. 4ta. ed. 1986.

4. Garzon D. "Análisis por elementos finitos del proceso de regeneración óseo". Universidad Nacional de Colombia. [Tesis de Maestría]; 2003.

5. Valbuena G, Villegas C, Roa M. Garzón D. Estudio de los esfuerzos mecánicos sobre prótesis de cadera". III Congreso Bolivariano de Ingeniería Mecánica (Paper Aceptado). Lima (Perú); 2003.

6. Bendsoe M, Sigmund O. Topology Optimization: theory, methods and applications. Springer Verlag; 2003.

7. Moaveni S. Finite element analysis: Theory and Applications with ANSYS. E.U.A: Nueva Jersey Ed. Prentice may. 1ra. ed; 1999.

8. Beer F, Johnston E. Mecánica de materiales. México: McGraw Hill. 4ta. ed.; 1993.

9. Flinn R, Trojan P. Materiales de ingeniería y sus aplicaciones. México: McGraw Hill. 3ra. ed; 1991.

10. Hughes TJR. The Finite Element Method-linear static and dynamic finite element Analysis. New York: Dover Publishers; 2000.

11. Fernández P, Rubén R. Optimizacao de forma de proteses da articulacao da anca. Madrid (España). Métodos Numéricos en Ingeniería V (SEMNI). 3ra. ed.; 2002.

12. Cojín S. Bone mechanics handbook. CRC Press Boca Raton (E.U.A). 2nd ed.; 2001.

13. Turner, et al. "The elastic propierties of trabecular and cortical bone tisues are similar: results from two microscopic measurement techniques". Londres (Inglaterra). J. Biomechanics. Elsevier Science Ltd. 1999;32(7):437-50.

14. McNamara B, et al. "Relationship between bone - prosthesis bonding and load transfer in total hip reconstruction". Londres (Inglaterra). J. Biomechanics. Elsevier Science Ltd. 1997;30(6):621-30.

 

 

Recibido: 25 de septiembre de 2008.
Aprobado: 15 de octubre de 2008.

 

 

Dsc. Diego Alexander Garzón-Alvarado. Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia, Bogotá, Colombia. E-mail: [e-mail]