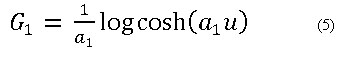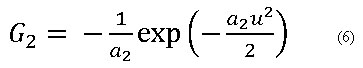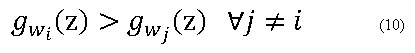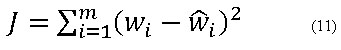Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Electrónica, Automática y Comunicaciones
versión On-line ISSN 1815-5928
EAC vol.35 no.2 La Habana Mayo.-ago. 2014
ARTICULO ORIGINAL
Una propuesta para configurar el algoritmo FastICA en el diagnóstico de fallos en sistemas industriales
A procedure to configure the FastICA algorithm in fault diagnosis on industrial systems
Ing. Marcos Quiñones Grueiro, Dr. Alberto Prieto-Moreno, Dr. Orestes Llanes Santiago
Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba. E-mail: marcosqg@electrica.cujae.edu.cu , orestes@electrica.cujae.edu.cu , albprieto@electrica.cujae.edu.cu
RESUMEN
El Análisis de Componentes Independientes (ICA) es una técnica estadística que ha sido ampliamente aplicada en los últimos diez años para la reducción de la dimensión en el diagnóstico de fallos en sistemas industriales. El algoritmo más usado es el denominado FastICA y dos de los parámetros más importantes del mismo para lograr una buena clasificación son la medida de la independencia y el criterio a seguir para la selección de las componentes independientes. En este trabajo se presenta una propuesta de procedimiento para determinar la mejor combinación entre estos dos parámetros en función de reducir la dimensión y lograr una buena tasa de aciertos en la clasificación. Para probar el procedimiento propuesto se emplearon los datos de simulación del modelo del proceso industrial Tennessee Eastman Process.
Palabras claves: procesos industriales, diagnóstico de fallos, análisis de componentes independientes, reducción de la dimensión.
ABSTRACT
Independent Component Analysis (ICA) is a statistical technique applied through the last ten years for dimensionality reduction in fault diagnosis on industrial systems. FastICA is the most popular algorithm in order to find the independent components. The independence measure and the feature selection criteria are two of the most important parameters to set on this algorithm. We propose in this paper a procedure to find a good combination of them based on achieve a good classification rate reducing the dimension of data the most possible. The proposed procedure is applied on the Tennessee Eastman Process plantas a model study.
Key words: industrial processes, independent component analysis, fault diagnosis, dimensionality reduction.
1. INTRODUCCIÓN
En la actualidad, la necesidad de mejorar el desempeño en los procesos productivos es creciente. Las paradas no planificadas y los fallos en el equipamiento pueden tener un impacto desfavorable en la economía de las plantas, en la seguridad del personal que las opera y provocar afectaciones significativas al medio ambiente. La detección temprana de un desempeño degradado del proceso y fallos en el sistema tecnológico se está convirtiendo en un requisito fundamental para sostener la capacidad productiva de una planta, su rentabilidad y su seguridad.1, 2 Una vía para evitar o enfrentar estas situaciones es hacer un mayor uso de los datos que son coleccionados de una planta. La llegada de sistemas modernos de medición y la automatización han implicado un aumento significativo de la cantidad de datos puestos a disposición de los operadores e ingenieros de las plantas. Desafortunadamente es muy común que la cantidad de información existente exceda la capacidad de interpretación humana y sea difícil darle seguimiento a la condición de los procesos.
La tarea del diagnóstico de fallos es identificar una causa asignable a partir de un estado de mal funcionamiento detectado, con el objetivo de proporcionar alertas tempranas de procesos fuera de especificación y realizar posteriormente las acciones correctivas apropiadas.3
En el diagnóstico de fallos basado en datos, así como en muchos problemas de análisis de datos, es muy común disponer de un conjunto de datos históricos de tamaño reducido (pequeño número de muestras) y un número elevado de variables de proceso, lo que limita el desempeño de los clasificadores.4 Con el objetivo de evitar este problema, conocido como «curso de la dimensionalidad», se han desarrollado y aplicado múltiples técnicas de reducción de dimensión, tales como: análisis de componentes principales (PCA),5 análisis de componentes independientes (ICA)69 y análisis discriminante de Fisher (FDA),10 para transformar todos los atributos hacia una dimensión menor que capture la información dominante del conjunto original de atributos.
ICA ha ganado popularidad en diferentes disciplinas tales como el procesamiento de señales,11 reconocimiento y visualización de imágenes12 y análisis financiero.13
En los últimos diez años la aplicación de ICA en la industria de procesos, como técnica de extracción de características, ha demostrado resultados muy positivos en el área del diagnóstico de fallos.6, 8, 9 En diferentes trabajos ha sido probada su superioridad respecto a PCA en cuanto a monitorización y clasificación.8 Uno de los algoritmos más populares es el llamado FastICA.69, 14 Todos estos algoritmos tienen parámetros que son necesarios ajustar para lograr la mejor estimación de las componentes independientes para el diagnóstico.
Después de calculadas estas últimas existen diferentes criterios para la selección de las más relevantes para el diagnóstico. Uno de los más utilizados es la independencia estadística utilizando medidas de la no gaussianidad 15, 16 y otro es la capacidad de las componentes independientes para capturar la varianza de las variables del proceso.7, 17 Este último es similar al que utiliza la técnica PCA.18
Para alcanzar los mejores resultados en el diagnóstico es importante lograr la mejor combinación entre el algoritmo para la estimación de los componentes independientes y el criterio para la selección de estas, sin embargo, en la literatura consultada no se logró encontrar un procedimiento que permita realizar esto. El objetivo principal de este trabajo es proponer un procedimiento que permita definir, dado un clasificador, cual es la combinación con la que se logra reducir más la dimensión del espacio, manteniendo una buena tasa de aciertos en la clasificación.
El procedimiento propuesto fue probado con los clasificadores Máxima Probabilidad a Posteriori (MAP),19 Vecino Más Cercano (VMC), Redes Neuronales Artificiales (RNA)26 y Máquinas de Soporte Vectorial (MSV).20 La estructura del trabajo es la siguiente. La sección 2 presenta el enfoque utilizado para reducir la dimensión del espacio de mediciones y el algoritmo FastICA. La sección 3 presenta la descripción del procedimiento propuesto. Los elementos fundamentales de los clasificadores utilizados se presentan en la sección 4. En la sección 5 se describe el problema de prueba Tennessee Eastman Process. Los resultados experimentales al aplicar dicho procedimiento y un debate basado en el análisis del desempeño de los clasificadores utilizados aparecen en la sección6. Finalmente, son presentadas las conclusiones.
2. CARACTERÍSTICASDEL ANÁLISIS DE COMPONENTES INDEPENDIENTES. EL ALGORITMO FASTICA
2.1. Reducción de la dimensión
En los procesos industriales la dimensión del vector de mediciones (el número de sensores), puede ser muy grande, y muchos de sus elementos pueden ser redundantes o incluso irrelevantes con respecto al proceso de clasificación.
Existen múltiples razones para reducir la dimensión de un vector de mediciones a un mínimo suficiente. La complejidad computacional es una razón obvia. Otra razón muy importante es que un incremento excesivo de la dimensión causa un decremento del desempeño del clasificador cuando no se poseen suficientes datos de cada variable.21
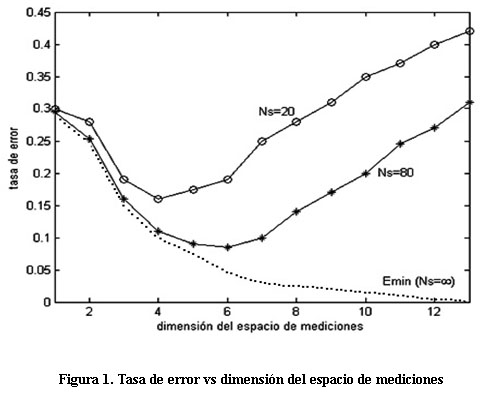
La Figura 1 ilustra como el uso de técnicas de reducción de dimensión puede simplificar y mejorar positivamente el procedimiento de diagnóstico en estos casos. El eje de las abscisas muestra el número de variables utilizadas para la clasificación, el eje de las ordenadas muestra la tasa de error y Ns indica la cantidad de muestras de cada variable para cada experimento. En el caso ideal, cuando Ns'! « y al utilizar todas las variables, se observa que el error de clasificación se aproxima a cero. Sin embargo, cuando se poseen pocas observaciones respecto al número de variables utilizadas el error de clasificación puede aumentar en la medida en que se incorporen nuevas variables.
Para proyectar los datos hacia un espacio de menor dimensión pueden utilizarse dos enfoques diferentes, la selección de características o la extracción de características. La selección de características descarta ciertos elementos del vector y selecciona aquellos que son más adecuados para la clasificación. Esto implica eliminar la información de las variables menos relevantes, lo cual significa que las variables eliminadas no contribuyen al sistema de diagnóstico, por lo que se pierde la posibilidad de detectar futuros fallos que las puedan afectar. En la extracción de características la selección de los elementos tiene lugar en un espacio de mediciones trasformado. Esto permite mantener la contribución de todas las variables al sistema de diagnóstico, ya que las características en el espacio trasformado se obtienen como una combinación de las variables originales.
2.2. Análisis de componentes independientes.
ICA es una técnica emergente para la reducción de dimensión en diagnóstico de fallos, la cual tiene como objetivo encontrar, a partir de una transformación lineal, una representación de un conjunto de variables donde se minimice la dependencia estadística entre las nuevas variables que la forman, llamadas componentes independientes. La independencia estadística entre un conjunto de variables implica que la función de densidad de probabilidad (fdp) conjunta de todas estas es igual al producto de las funciones de densidad de probabilidad marginal de cada una.22
Numerosos algoritmos se han propuesto para estimar las componentes independientes. Sin embargo, uno de ellos es el más reportado por la literatura científica aplicado al diagnóstico de fallos debido a su sencilla implementación y eficiencia computacional, este es conocido como FastICA.22
2.2.1. Configuración del algoritmo FastICA.
El algoritmo FastICA se basa en estimar las componentes independientes a partir del denominado modelo ICA libre de ruido y que se presenta a continuación:
Definición 1.El modelo ICA de un conjunto de n variables aleatorias x = (x1, x2, ..., xn)T , consiste en:(ecuación 1)
donde s = (s1, s2, . . . , sn)T es un conjunto de variables aleatorias estadísticamente independientes y A es una matriz cuadrada, llamada matriz de mezcla.
Las dos versiones del algoritmo más aplicadas son FastICA basado en maximización de la no gaussianidad y FastICA basado en estimación de la máxima probabilidad de independencia.22 En el campo del diagnóstico de fallos el primero ha conseguido gran aceptación y se ha aplicado en la mayoría de los trabajos presentados que utilizan esta técnica.9, 14 Este se basa en el Teorema Central del Límite, de forma que si dado un conjunto de variables se busca una combinación lineal de ellas que tenga una función de densidad de probabilidad (fdp) máximamente no gaussiana, se puede encontrar una de las componentes independientes. Por ello se seleccionará este último para estimar las componentes independientes en este trabajo.
Un primer criterio para configurar FastICA se relaciona con la manera en que se estiman las componentes independientes: secuencialmente o en paralelo.
La estimación secuencial resulta ventajosa en los casos en que existe un número muy grande de variables observadas y la estimación de todas las componentes independientes puede resultar un proceso muy lento. La desventaja de utilizar la estimación secuencial radica en que luego de encontrado el primer vector de la matriz de separación, cada vez que se encuentre uno nuevo, al ortogonalizar este respecto a los anteriores, se introduce un error numérico que debilita la condición de independencia estadística entre el total de los vectores.22
Cuando se utiliza la estimación en paralelo no se arrastra tal error22, pues en cada iteración se estima la matriz de separación completa y luego se ortogonalizan todos los vectores a la vez. Por ello, en este trabajo, se optó por aplicar el algoritmo FastICA con estimación de forma paralela. En la literatura se diferencian la estimación secuencial y la paralela en base al tipo de ortogonalización que se realiza en cada algoritmo: deflacionaria o simétrica.22
Finalmente el parámetro fundamental para configurar FastICA es la medida de no gaussianidad a utilizar para estimar las componentes independientes.
En el año 1997 se comienza a utilizar como medida de la no gaussianidad la Kurtosis.22 En 1999, se señala esta como una medida poco robusta y se comienza a utilizar la Entropía Negativa, que es una forma normalizada de la Entropía Diferencial.22 Esta se basa en utilizar la entropía como medida de la no gaussianidad y su fundamento está en el hecho de que las variables aleatorias con fdp gaussiana tienen la mayor cantidad de entropía entre todas las distribuciones con la misma varianza. La entropía negativa se representa a través de la siguiente función: (ecuación 2)
onde ygauss es una variable con distribución de probabilidad gaussiana que tiene la misma matriz de correlación(covarianza) que la variable aleatoria y. H es la Entropía Diferencial y se define como:
Definición 2. La Entropía Diferencial de una variable y con función de densidad de probabilidad py(ç) puede definirse como: (ecuación 3)
Para calcular la entropía negativa a partir de la ecuación (2) sería necesario conocer previamente o estimar la distribución de probabilidad de la variable y. En la mayoría de los casos esta es desconocida de antemano y el proceso para estimarla puede convertirse en un problema bastante engorroso y computacionalmente complicado, por ello se recomienda emplear aproximaciones de la Entropía Negativa.22 La más utilizada en este contexto se obtiene mediante: (ecuación 4)
donde G puede ser prácticamente cualquier función no cuadrática, v es una variable con función de densidad de probabilidad gaussiana y tanto y como v tienen media cero y varianza unitaria.
Se han buscado funciones no cuadráticas que permitan obtener medidas robustas de la no gaussianidad ante la presencia de datos fuera de rango. Dos que se muestran como buenas opciones son22: (ecuación 5 y 6)
La función G1 denominada por los autores como Tanh y G2 llamada como Gauss.22 En los trabajos que aplican este algoritmo reportados en el área de diagnóstico de fallos en procesos industriales se ha utilizado en su mayoría como
medida de la no gaussianidad G1, pues los autores del algoritmo FastICA la presentan como una buena opción para su aplicación de forma general.22 Sin embargo ellos también destacan que G2 es la medida más robusta ante datos fuera de rango debido a sus propiedades matemáticas23y no se ha encontrado en la literatura consultada sobre el diagnóstico de fallos un análisis comparativo sobre la utilización de G1 y G2 . Por ello en este trabajo se utilizará como medida de la no gaussianidad la Entropía Negativa tanto con G1, como con G2, pues resulta de interés comparar el uso de estas en la estimación de las componentes independientes para determinar con cuál se consigue el mejor diagnóstico posible.
2.2.2. Estrategias para la selección de las componentes independientes al aplicar ICA.
Al contrario de otras técnicas de extracción de características como PCA, que brinda las componentes principales ordenadas de acuerdo al grado de variabilidad que capturan de los vectores de mediciones originales, las variantes del algoritmo FastICA no estiman las componentes independientes siguiendo algún criterio para su disposición. Sin embargo, posterior a la estimación existen varias estrategias a seguir para ordenar las componentes independientes y seleccionar así un número menor de estas para realizar la tarea de clasificación.
Una estrategia muy popular, y una de las que se va a utilizar en este trabajo, es privilegiar la selección de las componentes independientes que más variabilidad capturen de las variables originales. Este criterio resulta semejante al que sigue PCA18 y se denominará como ordenamiento por información (Info).
Otra estrategia puede ser, según los autores del algoritmo FastICA, seleccionar las componentes máximamente no gaussianas de acuerdo al nivel de no gaussianidad que sigan sus distribuciones de probabilidad. Para ello pueden utilizarse diversos estadísticos, pero para ser consecuentes con la parametrización de FastICA se tomará como medida de la no gaussianidad a la Entropía Negativa y se denominará esta forma de ordenamiento por independencia (Ind).
Por último se realizará la selección de las componentes independientes en el mismo orden en que son estimadas de modo natural por el algoritmo FastICA, pues se desea conocer si se consiguen mejoras significativas al reordenarlas siguiendo los criterios mencionados anteriormente.
3. DESCRIPCIÓN DEL PROCEDIMIENTO PROPUESTO
A continuación se presenta el procedimiento propuesto en el cual es muy importante la experiencia acumulada por los expertos del proceso industrial que se trate.
Primer paso: Seleccionar la medida de desempeño ante la reducción para cada dimensión del espacio. Se pueden seguir diversas estrategias para ello, por ejemplo:
· A partir de un estudio de la ocurrencia de los fallos en la industria, darle mayor importancia a la clasificación correcta de los fallos más probables.
· Darle más peso a la clasificación correcta de los fallos que afectan la seguridad de los trabajadores de la planta y luego a los que causan las afectaciones económicas más significativas.
· Cuando no se posee un estudio muy profundo de la planta tomar como medida de desempeño la precisión general calculada a partir de aplicar la validación cruzada, pues constituye una medida general de la correcta clasificación de todos los fallos.
Segundo paso: Seleccionar el rango de componentes con que se desea trabajar de acuerdo a la dimensión del espacio de mediciones y al poder de cómputo disponible. Cuando los procesos incluyen un número elevado de variables y no se cuenta con un alto poder de cómputo, se puede tomar un número pequeño de componentes independientes. De no conseguirse el desempeño deseado con el rango escogido se debe incluir una mayor cantidad de componentes.
Tercer Paso: Seleccionar las variantes de configuración del algoritmo FastICA a comparar y cómo se va a parametrizar cada una.
Cuarto Paso: Determinar las estrategias a seguir para seleccionar las componentes independientes.
Quinto Paso: Determinar para cada configuración de FastICA la estrategia de selección de las componentes que resulte mejor según los requerimientos particulares del caso de estudio, como pueden ser:
· Desempeño: Establecer un desempeño mínimo requerido y determinar la estrategia de selección para la cual se alcanza este desempeño con el menor número de componentes.
· Necesidad de cómputo: Establecer un número de componentes con que se desea trabajar y escoger la estrategia de selección con que se alcanza mejor desempeño.
Sexto Paso: Realizar la comparación entre las configuraciones de FastICA.
4. CLASIFICADORES PARA EL DIAGNÓSTICO
En esta sección se presentan los aspectos teóricos básicos de los clasificadores utilizados en el trabajo, los cuales son los más reportados en la bibliografía.
4.1. Clasificador MAP
El clasificador de máxima probabilidad a posteriori (MAP) está inspirado en la teoría de decisión de Bayes. Esta técnica implementa la prueba de la razón de probabilidad de Bayes, la cual es óptima en el sentido que minimiza el costo o la probabilidad del error.24La probabilidad del error puede ser minimizada mediante el uso de la función de clasificación: (ecuación 7)
donde P (ωi|z) es la probabilidad a posteriori del vector de mediciones z de pertenecer a la clase ùi. Usando la regla de Bayes, puede mostrarse que ocurre la misma clasificación cuando (7) es reemplazada por: (ecuación 8)
donde p(z | ùi) es la función de densidad de probabilidad de z condicionada en ùi.
En este análisis es común suponer que las observaciones del vector característico z tienen una distribución normal y que la probabilidad a priori para cada una de las clases es la misma. Después de algún tratamiento matemático se obtiene que la función de clasificación está dada por: (ecuación 9)
donde ![]() es el vector de medias para la clase ωi y
es el vector de medias para la clase ωi y ![]() es la matriz de covarianza de las muestras para la clase ωi. El clasificador asigna una observación a la clase ωi para la cual el valor de la función de clasificación es máxima: (ecuación 10)
es la matriz de covarianza de las muestras para la clase ωi. El clasificador asigna una observación a la clase ωi para la cual el valor de la función de clasificación es máxima: (ecuación 10)
4.2. Clasificador Vecino Más Cercano (VMC)
El método de los k-Vecinos Más Cercanos (VMC) resulta uno de los pioneros en ser utilizados en problemas de clasificación de un conjunto de datos. Su nombre se deriva del principio que sigue para la clasificación, basándose en las vecindades entre los patrones para asignarlos a cada clase.25
Para utilizar este clasificador existen dos parámetros a elegir: el tipo de distancia para medir las vecindades y la cantidad de votos (vecinos) a tener en cuenta. El tipo de distancia utilizada en este trabajo es la euclideana y para decidir la cantidad de votos k que será tenida en cuenta para cada número de componentes retenidas se desarrolló el algoritmo 1 basado en utilizar la prueba de Wilcoxon para muestras pareadas.
ALGORITMO 1. Selección de la mejor arquitectura del clasificador KNN
{k1: Número de votos (vecinos) a tener en cuenta en la arquitectura 1
k2: Número de votos (vecinos) a tener en cuenta en la arquitectura 2
H0: Hipótesis nula, asume igualdad entre los desempeñosH0:ñk1=ñk2
ñk1: Desempeño para k1 vecinos
ñk2: Desempeño para k2vecinos
{ Valores iniciales: k1 = 3, k2 = 5}
repeat
ñk1! Calcular Desempeño(k1)
ñk2! Calcular Desempeño(k2)
if !(H0: ñk1=ñk2 )
thenif ñk2>ñk 1then
k1 = k2 ; k2 = k2 + 2
end if
end if
untilH0
selectk1
4.3. Clasificador Redes Neuronales Artificiales (RNA)
Las redes neuronales artificiales son herramientas de aprendizaje y procesamiento automático con una gran capacidad de aprendizaje y que se han destacado por su gran poder de generalización. Entre las múltiples arquitecturas existentes, se utilizará la perceptrón multicapa debido a su facilidad de implementación y el tamaño final de la red.26
Este tipo de red utiliza para su entrenamiento el algoritmo conocido como retropropagación del error, el cual, para un conjunto de datos de entrenamiento dado por (ωi, zi), intenta minimizar la expresión: (ecuación 11)
4.4. Clasificador Máquinas de Soporte Vectorial (MSV).
Las máquinas de soporte vectorial constituyen herramientas basadas en el aprendizaje estadístico. La tarea de los algoritmos en el aprendizaje de las MSV es buscar un hiperplano, a partir de vectores de soporte (puntos del espacio), que separe de forma óptima al espacio muestral de las diferentes clases, posiblemente, en un espacio de dimensionalidad superior.20
El utilizar las MSV para la clasificación se considera como un problema de clasificación binaria y las estrategias más utilizadas para la clasificación binaria son: uno contra uno y uno contra todos. Al emplear la primera, la cantidad de máquinas de soporte resultantes n se calculan a partir de la siguiente ecuación 12:
donde L es el número de clases. Al utilizar como estrategia la de uno contra todos, la cantidad de máquinas resultantes se calculan como: (ecuación 13)
Para procesos con muchas clases al aplicar la segunda estrategia el número de máquinas de soporte es mucho menor, implicando un ahorro de tiempo de cómputo que puede resultar significativo.
Se utilizará como función Kernel para la MSV el Kernel Gaussiano por ser uno de los más reportados en la literatura referente al diagnóstico de fallos.27 Para encontrar el valor óptimo del ancho de la campana de Gauss de la función Kernel Gaussiana, de forma que se minimice el error de clasificación para cada máquina de soporte, se utilizó como herramienta los algoritmos genéticos de la forma en que se presenta en los trabajos de Jack y Nandi27 y Rojas28.
5. CASO DE ESTUDIO
El Tennessee Eastman Process (TEP) fue desarrollado por la compañía Eastman Chemical para proporcionar un modelo de un proceso industrial real. El TEP ha sido ampliamente utilizado para probar el diseño de diferentes alternativas de control, estrategias de optimización y métodos de monitorización y diagnóstico.29
5.1. Diagrama de flujo del proceso.
En la planta se representa un proceso químico formado por varias unidades de operación, entre ellas: un reactor, un condensador, un compresor, un separador y una columna de destilación. El diagrama de flujo se presenta en la Figura 2. Los materiales gaseosos A, C, D y E y el inerte B son alimentados al reactor donde se forman los productos líquidos G y H. Además, se genera el subproducto F.
El flujo del producto obtenido en el reactor es enfriado a través de un condensador y luego alimentado a un separador vapor-líquido. El vapor existente en el separador es reciclado hacia la entrada del reactor a través de un compresor. Una porción del flujo reciclado es purgada para mantener la cantidad de material inerte y de subproducto acumulado en el proceso. Los componentes condensados son bombeados desde el separador hacia el limpiador de impurezas. Los productos G y H existentes en la base del limpiador son enviados a un proceso que no está incluido en el diagrama.
5.2. Variables del proceso y fallos
La simulación de la planta involucra un total de 51 variables: 22 variables de proceso, 19 de estado y 11 manipuladas. Para realizar el diagnóstico de fallos se utilizaron solo las 33 variables, que se encuentran disponibles para medir en línea. Todas las mediciones al proceso incluyen ruido Gaussiano. Por medio de la manipulación de dichas perturbaciones, en el TEP pueden generarse 21 fallos pre-programados, 16 de los cuales son conocidos y cinco desconocidos. Estos fallos son asociados con cambios tipo paso en las variables del proceso, incrementos en la variabilidad de las variables del proceso, y fallos en los actuadores tales como atascamiento de las válvulas. Las simulaciones realizadas para generar las condiciones de fallo utilizaron el esquema de control para la planta completa descrito por Lyman y Georgakis.30
5.3. Selección de los datos
Para probar el procedimiento propuesto se seleccionaron 15 de los 21 fallos pre-programados, los cuales ocurren en las zonas de alimentación, el reactor, y el condensador. Siete de los fallos son causados por cambios tipo paso en las variables del proceso, cinco por el incremento de la variabilidad de las variables, dos por atascamientos en las válvulas y uno por la desviación lenta en la dinámica de la reacción y se presentan en la Tabla 1.
Se trabajó con el conjunto de datos históricos del proceso presentado por Downs,29 el cual está formado por 7249 muestras, de las que 490 corresponden al estado de funcionamiento normal y el resto corresponde a los 15 fallos simulados, estos datos representan el funcionamiento histórico de las 33 variables seleccionadas.
RESULTADOS Y DISCUSIÓN
Al desarrollar el procedimiento no se contaba con datos sobre las probabilidades de ocurrencia de los fallos en el problema de prueba, ni con un estudio profundo de las consecuencias económicas y para la seguridad de la planta de cada uno de estos. Por ello se escogió, como medida de desempeño, la precisión general a partir de aplicar la validación cruzada con p=10, donde p es el número de particiones utilizadas.
A continuación partiendo de que el caso de estudio utilizado en este trabajo tiene una dimensión de 33 componentes, se tomó un rango desde 1 hasta 32. Ello está determinado porque se desea explorar las potencialidades del clasificador en casi la totalidad del espacio. No se analizará para 33 porque no habría reducción de la dimensión.
Luego las configuraciones a comparar, dado que se utilizó el algoritmo FastICA basado en maximización de la no gaussianidad, se diferencian en la selección de G1 óG2 . El resto de la parametrización del algoritmo se explicó en la sección 2.2.1 y las estrategias de selección a utilizar fueron presentadas en la sección 2.2.2.
Se pretende determinar la estrategia de selección de las componentes independientes que mejor resultados ofrece para cada configuración de FastICA. Como requerimiento en nuestro caso de estudio, a partir del número de variables involucradas y la cantidad de fallos, se tomó un mínimo de desempeño de un 80 % de precisión general. Pues en los procesos industriales los expertos consideran el 80% como el mínimo desempeño para tomar un criterio de decisión respecto a la clasificación de fallos. Para ilustrar como se escogió la mejor variante en cada caso se presenta uno de los resultados obtenidos con el clasificador MAP en la siguiente Figura 3.
En la parte superior de esta figura se muestra cómo evoluciona la precisión general de la clasificación en función de la cantidad de componentes retenidas para cada estrategia de selección. En el gráfico de barras inferior se muestra para cada número de componentes con qué estrategia se consigue la mejor precisión general. Este gráfico es el resultado de aplicar a partir de la validación cruzada la prueba de hipótesis de Friedman primeramente, para ver si hay diferencias significativas entre los resultados de clasificación y si se existen estas se aplica la prueba de Wilcoxon con un sistema de votos para decidir cuál o cuáles de las tres estrategias es la mejor.
En esta Figura 3, por ejemplo, puede observarse que, aunque a simple vista las tres estrategias de selección ofrecen resultados similares, para las primeras diez componentes la selección por independencia ofrece generalmente los mejores resultados; mientras que a partir de las once componentes y luego de alcanzarse el 80 % de precisión general la selección por información resulta superior. Por ello esta se selecciona como la mejor para esta configuración.
El resumen de los resultados obtenidos para cada clasificador al realizar un análisis similar se muestran en la Tabla 2. En ella se muestra la estrategia de selección de características escogida para cada clasificador y configuración de FastICA. Por ejemplo, para el clasificador VMC al utilizar FastICA con G1 la mejor estrategia de selección es por información. Además se destaca para cada combinación la cantidad de componentes necesarias para alcanzar el 80 % de desempeño, siendo necesarias en este último ejemplo solo 8 componentes.
Se puede apreciar que con todos los clasificadores se logra el desempeño antes mencionado antes de las 15 componentes. La cantidad de componentes para alcanzarlo con MAP es igual a VMC, del mismo modo con RNA y MSV es similar. Además, como se aprecia en la Tabla 2, para todos los clasificadores se obtuvieron las mismas combinaciones entre la configuración de FastICA y la estrategia de selección de las componentes.
A continuación se procedió a comparar las configuraciones de FastICA. Los resultados mostraron que los desempeños de los clasificadores son muy similares. Ello muestra que el escoger una estrategia de selección de características acorde a la configuración de FastICA y al clasificador, resulta un paso esencial para obtener los mejores desempeños posibles.
Además de forma general seobservó que para alcanzar un 80 % de precisión general se necesitan de 7 a 15 componentes independientes según el clasificador que se utilice. Puede afirmarse además que las primeras quince componentes aportan la información más relevante para el desempeño de los cuatros clasificadores empleados, pues al incorporar las últimas 17 solo se logra incrementar el desempeño de un 2 % a un 4 %.
Por último en la Figura 4 puede observarse la comparación entre los mejores resultados de los cuatro clasificadores.
Para la reducción de la dimensión los que ofrecen mejores resultados son el MAP y el VMC, pues con solo ocho componentes superan el 80 % de precisión general y ya con 15 componentes alcanzan el 85 %. Esta conclusión apoya la suposición de que el pre-procesamiento con ICA aproxima las características de los datos a las condiciones que garantizan los mejores resultados de clasificación para el MAP y VMC. La mejora que introduce ICA se debe a que, al estructurar de forma más organizada las distribuciones de probabilidad de las variables provoca a su vez una mejor estructuración de los clúster de datos y de esa forma se disminuye la confusión que puede aparecer cuando la estructura de estos es más dispersa.
CONCLUSIONES
En este artículo se presentó un procedimiento para comparar varios criterios de selección de características y métodos de extracción de características. El objetivo principal de este es seleccionar la mejor configuración en el pre-procesamiento de los datos y conseguir así un buen desempeño al reducir la dimensión del espacio.
Se aplicó el mismo en cuatro clasificadores diferentes para obtener la mejor configuración en el pre-procesamiento al aplicar ICA como técnica de extracción de características. Se escogió como problema de prueba el TEP y fue utilizado el algoritmo FastICA para estimar las componentes independientes utilizando la Entropía Negativa como medida de independencia. Se compararon dos métodos para la selección de las componentes independientes de los más utilizados respecto a emplear las componentes en el mismo orden en que son estimadas. Luego de encontrar el mejor criterio para seleccionar las componentes independientes se realizó la comparación de los resultados al utilizar dos funciones para parametrizar la Entropía Negativa.
Al aplicar el procedimiento se obtuvieron las mejores configuraciones en el pre-procesamiento de los datos para cada clasificador. De modo general al utilizar como medida de la no gaussianidadG1 se obtuvieron mejores resultados al seleccionar las componentes de acuerdo a la información. Sin embargo al aplicar G2 no se apreció ventajas significativas al seleccionar las componentes de modo diferente al que fueron estimadas. Cabe destacar que al tomar el mejor criterio de selección de las componentes con cada función de la Entropía Negativa no se aprecian diferencias sustanciales al compararlas en cuanto al criterio establecido.
A pesar de su simplicidad y antigüedad respecto a los otros clasificadores, los clasificadores con mejores resultados son MAP y VMC. Ello puede estar motivado porque ICA al mejorar la estructura de los datos brinda mayor claridad para los principios de clasificación que siguen estos métodos.
REFERENCIAS
1. R. ISERMANN, Fault Diagnosis Applications. Ed.Springer. Berlin 2011.
2. V. PALADE, C. D. BOCANIALA, and L. JAIN, Computational Intelligence in Fault Diagnosis. Ed. Springer. London 2006.
3. B. M. WISE and N. B. GALLAGHER, «The process chemometrics approach to process monitoring and fault detection.»en Journal of Process Control, Vol. 6, pp. 329347, 1996.
4. K. R. RAO and S. LAKSHMINARAYANAN, «Partial correlation based variable selection approach for multivariate data classification methods.»en Chemometrics and Intelligent Laboratory Systems, Vol. 86, pp. 6781, 2007.
5. H. CHENG, M. NIKUS, and S.-L. JAMSLA-JOUNELA, «Evaluation of PCA methods with improved fault isolation capabilities on a paper machine simulator.»en Chemometrics and Intelligent Laboratory Systems, Vol. 92, pp.186199, 2008.
6. M. KANO, S. TANAKA, S. HASEBE, and I. HASHIMOTO, «Monitoring Independent Components for Fault Detection.» AIChE Journal, Vol. 48, No. 4, pp. 969976, 2003.
7. J.-M. LEE, C. YOO, and I.-B. LEE, «Statistical monitoring of dynamic processes based on dynamic independent component analysis.»en Chemical Engineering Science, Vol. 58, pp. 2995 3006, 2004.
8. A. WIDODO, B.-S. YANG, and T. HAN, «Combination of independent component analysis and support vector machines for intelligent faults diagnosis of induction motors.»en Expert Systems with Applications, Vol. 32, pp.299312, 2007.
9. A. AJAMI and M. DANESHVAR, «Data driven approach for fault detection and diagnosis of turbine in thermal power plant using Independent Component Analysis (ICA).» International Journal of Electrical Power & Energy Systems, Vol. 43, No. 1, pp. 728735, 2012.
10. Y. ZHOU, J. HAHN, and M. S. MANNAN, «Process monitoring based on classification tree and discriminant analysis.»en Reliability Engineering and System Safety, Vol. 91, pp. 535545, 2006.
11. J. MUNOZ, J. RIVERA, and E. DUQUE, «Principal and independent component analysis applied to noise reduction in electrocardiographic signals.» Scientia et Technica, No. 39, pp. 8388, 2008.
12. A. LEHRMANN, M. HUBER, A. C. POLATKAN, A. PRITZKAU, and K. NIESELT, «Visualizing dimensionality reduction of systems biology data.»en Data Mining and Knowledge Discovery, 2012.
13. C.-J. LU, T.-S. LEE, and C.-C. CHIU, «Financial time series forecasting using independent component analysis and support vector regression.»en Decision Support Systems, Vol. 46, pp. 115125, 2009.
14. J.-M. LEE and J. QUIN, «Fault detection and diagnosis based on modified independent component analysis.» AIChE Journal, Vol. 51, No. 10, pp. 34913504, 2006.
15. T. LAN, D. ERDOGMUS, A. ADAMI, M. PAVEL, and O. HEALTH, «Feature Selection by Independent Component Analysis and Mutual Information Maximization in EEG Signal Classification.»en IEEE International Joint Conference on Neural Networks., 2005, pp. 3011 3016.
16. M. PRASAD, A. SOWMYA, and I. KOCH, «Efficient Feature Selection based on Independent Component Analysis.»en Intelligent Sensors, Sensor Networks and Information Processing Conference. 2005, pp. 427 432.
17. T. VILLEGAS and M. J. FUENTE, «Fault diagnosis in a wastewater treatment plant using dynamic independent component analysis.»en 18th Mediterranean Conference on Control & Automation, Marrakech, Morocco, 2010, pp. 874879.
18. A. HYVÄRINEN, «Survey on independent component analysis.» Neural Computing Surveys, No. 2, pp. 94128,1999.
19. L. H. CHIANG, E. RUSELL, and R. D. BRAATZ, Fault Detection and Diagnosis in Industrial Systems. Ed. Springer-Verlang. London, England 2001.
20. A. WIDODO and B.-S. YANG, «Review. Support vector machine in machine condition monitoring and fault diagnosis.»en Mechanical Systems and Signal Processing, Vol. 21, pp. 25502563, 2007.
21. F. VAN DER HEIJDEN, R. P. W. DUIN, D. DE RIDDER, and D. M. J. TAX, Classification, Parameter Estimation and State Estimation: An Engineering Approach Using MATLAB. Ed. John Wiley & Sons, Ltd. England 2004.
22. A. HYVÄRINEN, J. KARHUNEN, and E. OJA, Independent Component Analysis. Ed.John Wiley & Sons, Inc.New York, USA 2001.
23. A. HYVÄRINEN, «Fast and Robust Fixed-Point Algorithms for Independent Component Analysis.»en IEEE Trans. on Neural Networks, pp. 116, 1999.
24. K. FUKUNAGA, Introduction to Statistical Pattern Recognition, 2nd ed. Ed. Academic Press.USA 1990.
25. N. BHATIA, «Survey of Nearest Neighbor Techniques.»en International Journal of Computer Science and Information Security, Vol. 8, pp. 302305, 2010.
26. K. PATAN, Artificial Neural Networks for the modeling and Fault Diagnosis of Technical Processes. Ed. Springer.Berlin 2008.
27. L. B. JACK and A. K. NANDI, «Fault detection using support vector machines and artificial neural networks, augmented by genetic algorithms.»en Mechanical Systems and Signal Processing., Vol. 16, pp. 373390, 2002.
28. S. A. ROJAS, «Adapting Multiple Kernel Parameters for Support Vector Machines using Genetic Algorithms.»en IEEE Congress on Evolutionary Computation, 2005, pp. 616621.
29. J. DOWNS and E. VOGEL, «Plant-wide industrial process control problem.» Computer and Chemical Engineering., No. 3, pp. 244254, 1993.
30. P. R. LYMAN and C. GEORGAKIS, «Plant-Wide Control of the Tennessee Eastman Problem.»en Computer andChemical Engineering.Vol. 19, pp. 321331, 1995.
Recibido: Abril 2014
Aprobado: Mayo 2014