ARTÍCULO ORIGINAL

 

Sistema de navegación basado en modelo dinámico no lineal de Vehículo Autónomo Sumergible

 

Autonomous Underwater Vehicle navigation system based on nonlinear vehicle dynamic model.

 

 

MSc. Delvis Garcia-Garcia, Msc. Yunier Valeriano-Medina, Ing. Jorge A. Portal-Linares, Dr. C. Luis Hernández Santana

Universidad Central de Las Villas (UCLV). Villa Clara, Cuba.

 

 

---

RESUMEN

Las investigaciones en relación con los Vehículos Autónomos Sumergibles (VAS) han tenido un gran auge en los últimos años debido fundamentalmente al desarrollo de las tecnologías de sensores y computadoras. En nuestro país el Grupo de Automatización, Robótica y Percepción conjuntamente con el Centro de Investigaciones Hidrográficas trabajan en el desarrollo de un VAS basado en una arquitectura de hardware de bajo costo. En el presente artículo se muestra el diseño de un sistema de navegación compuesto por un observador pasivo de estados. El algoritmo consta de un modelo no lineal del vehículo, al que se le han incorporado aproximaciones lineales para modelar las olas y las corrientes marinas. El procedimiento de sintonización resulta relativamente sencillo y el observador obtenido es factible de implementar en tiempo real. Los resultados de las simulaciones realizadas utilizando MatLab/Simulink. En las simulaciones realizadas utilizando MatLab/Simulink se observa una estimación adecuada de los parámetros de navegación y el filtrado de las perturbaciones marinas.

Palabras claves: navegación, no lineal, corrientes marinas, observador, oleaje.

---

ABSTRACT

Researches related Autonomous Underwater Vehicles (AUVs) have boomed in recent years mainly due to the development of sensors and computers technologies. In Cuba the Group of Automation, Robotics and Perception and the Hydrographic Research Center have been working on the development of an AUV based on low-cost hardware architecture. In this paper the design of a navigation system based on a passive observer is shown. The algorithm consists of a nonlinear model of the vehicle in combination with linear approximations of ocean waves and currents. The tuning procedure is relatively easy and the observer obtained is feasible to implement in real time. The simulations performed using MatLab/Simulink show good results in terms of disturbances rejection and estimation of navigation parameters needed like velocities and positions.

Key words: navigation, nonlinear model, ocean currents, observer, waves.

---

 

 

INTRODUCCION

 

En la actualidad se ha hecho cada vez más necesario el hecho de interactuar e investigar el medio marino, dándose el hombre la tarea de desarrollar distintos tipos y modelos de vehículos que le permitan adentrarse más en el mismo. Por esta razón muchas instituciones en todo el mundo se han dedicado al estudio y desarrollo de vehículos capaces de realizar investigaciones con la mayor eficacia posible; además de la disminución de los costos para llevar a cabo estas tareas ^{1 2 3}. Una de las tendencias actuales es el desarrollo de los Vehículos Autónomos Subacuáticos (VAS), estos han tenido una gran aceptación a nivel mundial debido a las ventajas que brindan en el cumplimiento de misiones de difícil acceso, donde se debe preservar la vida del hombre ⁴.

En Cuba la utilización de este tipo de tecnologías es aun reducida, sin embargo se llevan a cabo un conjunto de investigaciones para el desarrollo de un prototipo de vehículo empleando principalmente sensores y una arquitectura de hardware de bajo costo, a este vehículo se le llama HRC-AUV.

Para operar totalmente de manera autónoma un medio de este tipo, es necesario contar con un Sistema de Control de Movimiento (SCM) confiable y preciso, cuyo componente fundamental lo constituye el algoritmo de navegación ⁵. En la actualidad la precisión de los SCM está siendo cada vez mayor debido a la aplicación de nuevas técnicas de navegación y algoritmos de estimación ⁶. Para lograr un adecuado monitoreo de la navegación de un VAS se hace necesario el estudio de las principales perturbaciones que lo afectan, así como la búsqueda y propuesta de métodos o algoritmos que permitan contrarrestar estos efectos indeseables ^{7 8}.

Durante años han sido variadas las técnicas propuestas para filtrar el oleaje, las mismas incluyen filtro paso bajo, filtros notch y combinaciones de banda muerta o umbral. Todas estas alternativas tenían un desempeño limitado cuando era necesario ejecutar acciones de control fuertes sobre el vehículo, lo cual afectaba el comportamiento general del sistema ⁵. Los filtros que han mostrado un mejor desempeño son aquellos basados en un modelo del vehículo y modelos de las perturbaciones combinados en un observador de estados ^{2 6}. Alternativamente varios autores han explotado las potencialidades que brindan los observadores pasivos, tanto en variantes lineales como no lineales ^{3 8 9}.

En este trabajo se presenta el diseño de un observador pasivo empleando el modelo horizontal no lineal del vehículo, con el cual se obtiene una mayor exactitud y fidelidad con respecto al comportamiento real. Adicionalmente se incorporan aproximaciones lineales para representar el oleaje y las corrientes ⁵. La metodología empleada fue anteriormente utilizada con éxito en el diseño de un observador lineal para estimar el rumbo del vehículo ¹⁰. En este diseño no lineal el proceso de sintonización del observador puede resultar engorroso en comparación con las técnicas empleadas para el ajuste de observadores pasivos lineales ⁹. Se muestran los resultados de la implementación en MatLab/Simulink así como varias simulaciones realizadas con el sistema operando en lazo abierto y luego bajo control de dirección. Los valores estadísticos de los resultados confirman que el observador empleado es capaz de realizar estimaciones de los parámetros de navegación, al mismo tiempo que contrarresta los efectos de las perturbaciones modeladas.

 

SISTEMA DE COORDENADAS Y NOMENCLATURA EMPLEADOS

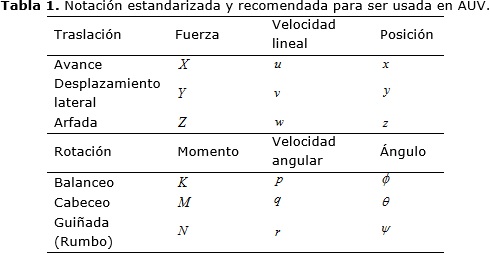
El movimiento de un submarino se describe con respecto a un marco de referencia inercial, para ello generalmente se considera que la aceleración en un punto de la superficie del planeta provocada por la rotación de la tierra no afecta el movimiento del mismo si este se mueve a baja velocidad ¹¹; como el caso del estudiado ya que se encuentra por debajo de los 2 m/s. Al tener esto en cuenta no se considera la razón de rotación de la Tierra y por lo tanto el sistema de coordenadas fijado al centro de la Tierra y cuyos ejes se mueven con ella es considerado un marco de referencia inercial y a la misma vez de navegación definido como Norte, Este, Abajo (en inglés, N.E.D.). En la Figura 1 se representan los sistemas empleados así como la definición de las variables de rotación y traslación del vehículo. La notación empleada en este trabajo se resume en la Tabla 1, la cual constituye la nomenclatura estandarizada y recomendada para para describir los movimientos y las fuerzas en vehículos que operan en el mar ¹².

MODELO NO LINEAL GENERAL DEL VEHICULO

Cuando se analiza el movimiento de los vehículos marinos en los 6 grados de libertad (GDL), resulta conveniente definir los dos sistemas de coordenadas presentados en la Figura 1. El origen del sistema del submarino (OB) puede ser situado en el Centro de Flotabilidad (CB) o en el Centro de Gravedad (CG), aprovechando el plano principal de simetría. En el caso particular del HRC-AUV, OB se hace coincidir con CB. Los siguientes vectores permiten describir el movimiento de un submarino en los 6 GDL.

Donde η denota al vector de posición y orientación con coordenadas en el sistema de referencia fijo en Tierra, v representa el vector de velocidad lineal y angular con coordenadas en el sistema del submarino y τ se utiliza para representar las fuerzas y momentos que actúan sobre el vehículo en el sistema de coordenadas del submarino. Finalmente las ecuaciones que describen el movimiento del vehículo en el espacio tridimensional pueden obtenerse a partir de las leyes de conservación de los momentos lineales y angulares referidos a un sistema inercial de referencia. En ^{5 8} se demuestra que la segunda ley de Newton puede expresarse para cualquier vehículo subacuático con un sistema de coordenadas fijo al cuerpo de la forma:

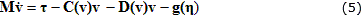
Siendo M=M_RB+M_A la matriz de inercia que incluye el término de masas añadidas M_A, C(v)=C_RB(v)+C_A(v) la matriz de Coriolis y de fuerza centrípeta que incluye también los efectos de masas añadidas en su segundo término, D(v) la matriz de amortiguamiento y g(η) constituye el vector de fuerzas y momentos gravitacionales. Adicionalmente R(n) representa la transformación de coordenadas del sistema cuerpo al plano de navegación tangente a la superficie de la Tierra. En este trabajo solo se utiliza este modelo general de 6 GDL con fines de simulación debido a la complejidad del mismo. Seguidamente se ilustra el modelo seleccionado para el diseño del observador no lineal, sintetizado a partir de este modelo general.

 

MODELO DEL VEHICULO PARA EL DISEÑO DEL OBSERVADOR

 

En los VAS es común dividir las ecuaciones de movimiento de 6 GDL en 3 subsistemas desacoplados o débilmente acoplados de 3 GDL cada uno, utilizados estos para el control y la navegación del vehículo en los planos x - z y x - y del sistema OE respectivamente ⁷.

· Subsistema longitudinal: empleado para las maniobras de emersión-inmersión. Comprende las variables de estado (u, w, q) y (x, z, Ψ).

· Subsistema lateral: utilizado para las maniobras de dirección. Variables de estado (v, p r) y (y, Φ, Ψ).

· Subsistema horizontal: utilizado para el diseño del sistema de navegación. Variables de estado (u, v, r) y (x, y, Ψ).

El movimiento en la superficie del mar o en un plano horizontal paralelo a la superficie de un vehículo marino se describe en función del avance, el desplazamiento lateral y del ángulo de guiñada (rumbo) que se corresponde con el subsistema horizontal como se describe anteriormente. Esto implica que la dinámica asociada al resto de los términos no sea tenida en cuenta; de manera que w=p=q=0 ⁵. Por lo tanto las matrices y vectores que determinan el modelo no lineal del vehículo para este subsistema quedan definidas como:

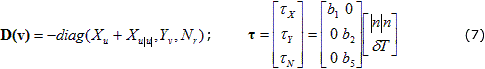
Este modelo no lineal de 3 GDL en espacio estado para el subsistema horizontal del HRC-AUV queda entonces definido en forma compacta como:

Este modelo es el que se utiliza para representar el movimiento del vehículo, referido como estados de baja frecuencia (BF) en el diseño del observador, que conjuntamente con los modelos de las perturbaciones de las siguientes secciones conforman el modelo del sistema. La obtención de estos modelos así como las pruebas realizadas para identificar cada parámetro se muestra de manera detallada en ¹³. Un resumen de los parámetros geométricos e inerciales del HRC-AUV utilizados en este trabajo se muestra en la Tabla 2.

Los relacionados con las masas añadidas e inerciales se calcularon aproximando el vehículo a un esferoide alargado, obteniéndose los siguientes valores: Xu^•=-250.84kg, Y_v^• =-3834kg, N_r^•=-15572kgm², I_zz=20816kgm².

 

MODELO DEL OLEAJE

 

Las principales perturbaciones que afectan a los vehículos subacuáticos durante la navegación lo constituyen el oleaje generado por el viento y las corrientes marinas ⁴. Para el caso del oleaje la respuesta es considerada de alta frecuencia (AF) en comparación con el movimiento del vehículo. Las señales del conjunto vehículo-oleaje se determinan mediante el principio de superposición lineal, donde el movimiento de 1er orden inducido por las olas η_olas=[x_olas , y_olas, Ψ_olas]^T se le añade a los componentes del movimiento de baja frecuencia (BF) de la embarcación representada por los estados del subsistema horizontal mostrado en la ecuación (8).

El comportamiento de las mareas constituye una suma infinita de términos sinusoidales, cada uno de los mismos con diferente amplitud, frecuencia y fase ^{14 15}. Mediante pruebas y análisis estadísticos de las mareas en distintas partes del mundo se han logrado obtener espectros que representan con suficiente exactitud los estados de operación del mar. Sin embargo, en los sistemas automáticos es conveniente tener una aproximación lineal del espectro de las olas que pueda ser incluida en los lazos de control de manera sencilla. En este sentido, es posible obtener una función de transferencia de segundo orden muy atractiva por su simplicidad y aplicabilidad, la cual fue propuesta inicialmente por autores como ¹. Luego se realizaron algunas mejoras mediante la inclusión de un término de amortiguamiento como se muestra en la función transferencia (9). En lo adelante se considera un modelo como el mostrado en la ecuación (9) para cada grado de libertad analizado.

Donde h_olas representa la amplitud del movimiento inducido por las olas, ω_0i(i=1, 2, 3) es la frecuencia fundamental de las olas para cada grado de libertad analizado, ζ_i(i=1, 2, 3) es el coeficiente de amortiguamiento que por lo general se selecciona en el rango entre 0.01-0.1 para que la aproximación de 2do orden (9) sea lo más cercana posible al comportamiento de las oscilaciones reales inducidas por las olas según el espectro. En ⁵ se muestra una estimación de este parámetro para diferentes estados del mar, concluyendo que no varía prácticamente ante cambios en la altura y frecuencia de las olas y se recomienda el valor 0.1 para representar el espectro Jonswap (en inglés, Join North Sea Wave Project) utilizado para mares poco desarrollados ¹⁵ como es el caso de los escenarios de operación del HRC-AUV. Adicionalmente K_ωi constituye un factor de ganancia ajustable relacionado con la intensidad del impacto de las olas sobre el vehículo. Para representar la función transferencia (9) en cada grado de libertad se emplean 2 estados por lo tanto su influencia en las tres variables estimadas conduce a una representación de 6 estados. Finalmente estos estados de AF correspondiente a los grados de libertad del oleaje se representan en forma matricial compacta tal como se muestra en (10):

Donde ξ₁ y ξ₂ son vectores columnas de tres elementos cada uno y adicionalmente:

MODELO DE LAS CORRIENTES MARINAS

En este caso el modelo del vehículo representa los tres grados de libertad solamente para navegar en superficie o en un plano paralelo a la misma, o sea, el denominado modelo horizontal. Consecuentemente con esto solamente se analiza la influencia de las corrientes oceánicas en un modelo bidimensional ¹⁶. Considerando que las mismas no generan movimientos de rotación en el vehículo, entonces el vector velocidad de la corriente referido al sistema de navegación sería:

Teniendo en cuenta únicamente el movimiento en un plano horizontal paralelo al plano x y, las componentes se describen solamente en función del módulo de la velocidad V_c= √(u_c² +v_c²) y el ángulo de desplazamiento lateral β_c. Esta aproximación es válida si se tiene en cuenta que el HRC-AUV operará en rangos de profundidad cercanos a la superficie, quedando:

Considerando que las fuerzas en avance y el balanceo, así como el momento de guiñada varían lentamente. Un modelo bidimensional frecuentemente utilizado para las aplicaciones de control marino es el proceso Gauss-Markow de primer orden mostrado en la expresión (18) y de manera compacta en (19):

Donde b es un vector columna de tres elementos el cual representa las fuerzas y momentos inducidos sobre el movimiento del móvil, w_b es un vector de ruido blanco, T_b es una matriz diagonal formada por las desviaciones (en inglés, drift) de cada variable y Ψ es una matriz diagonal escalar para regular la amplitud de w_b ^{6 16}.

SISTEMA DE MEDICION

La ecuación de medición de las distintas variables involucradas en el modelo horizontal del vehículo puede ser escrita de manera general como:

Donde η_olas representa el movimiento de AF del móvil debido a las perturbaciones de primer orden inducida por las olas y v es un vector de ruido blanco en las mediciones. También el observador necesita mediciones de la posición de los actuadores μ, tal que las fuerzas en avance, balanceo y momento de guiñada puedan ser calculadas según:

Finalmente considerando el modelo horizontal de 3 grados de libertad (8) con v = n = w = 0, así como las perturbaciones que lo afectan (10) y (19), se conforma el modelo general del sistema cuyas ecuaciones serían:

ECUACIONES DEL OBSERVADOR

Las ecuaciones del observador constituyen una copia de las ecuaciones dinámicas anteriores (22); incorporando además los términos de corrección formados por las ganancias y el error de estimación, quedando finalmente:

Donde y^ˆ=y-y^~ representa el error de estimación. Haciendo uso de la notación Δ=x-x^~ y sustrayendo las ecuaciones del observador (23) de las del sistema (22), se logra obtener la expresión dinámica para el error de estimación cuya representación en espacio de estados adquiere la forma:

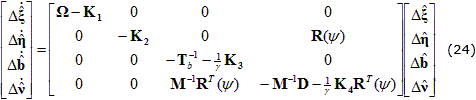
PROCEDIMIENTO DE SINTONIZACION

Muchos han sido los trabajos que han hecho uso en los últimos años de las técnicas no lineales en el diseño de observadores de estados, para la estimación de los distintos parámetros y variables necesarias en la navegación y el control ^{1 2 17}. Son varios los autores que emplean algoritmos pasivos entre los que destacan ^{3 9}; coincidiendo todos en la manera de calcular las ganancias del observador y mostrando un camino para llevar a cabo esta detallada tarea. Para sintonizar estas ganancias se hace uso de la teoría de estabilidad y pasividad de Lyapunov y en este trabajo se sigue un procedimiento similar al mostrado en ⁶. Para el caso específico del observador discutido, las expresiones generales para determinar cada uno de los componentes de las matrices de ganancias serían:

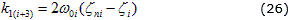
Siendo (i=1…3) y se debe asegurar además que:

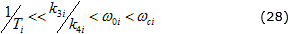
Donde se tiene que cumplir adicionalmente que ζ_ni > ζ_i y ω_ci > ω_0i, ya que estas variables representan el amortiguamiento y la frecuencia de corte de un filtro notch. Para lograr tal efecto en el filtrado adecuado de la frecuencia del oleaje se tiene que cumplir estas últimas condiciones. Con estos requisitos de selección se le otorga la siguiente estructura a las matrices de ganancia del observador:

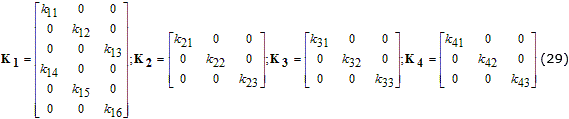
De acuerdo con la estructura mostrada para cada matriz de ganancia y teniendo en cuenta los requisitos para la selección de las constantes, se asegura entonces la estabilidad del observador y por lo tanto la convergencia del mismo.

 

RESULTADOS OBTENIDOS Y DISCUSION

 

El vehículo bajo estudio presenta una geometría cilíndrica, está equipado con un propulsor y dos timones; uno vertical y otro horizontal. Se han dedicado muchas sesiones de trabajo y experimentos a la obtención de un modelo matemático que represente toda la información posible de la dinámica del sistema con la suficiente fiabilidad y precisión. Afortunadamente en investigaciones anteriores se logró la obtención de un modelo de 6 GDL que ha sido validado mediante distintas pruebas. La estructura de este modelo así como las pruebas llevadas a cabo se muestran en el trabajo ¹³ En la presente investigación se hace uso de este modelo para realizar las simulaciones mostradas a continuación y la validación del algoritmo de navegación. Las características que se tuvieron en cuenta para las simulaciones fueron:

· Se incluyeron las fuerzas centrípetas y de Coriolis tanto en el modelo de simulación de 6 GDL del vehículo como en el modelo horizontal de 3 GDL utilizado para el diseño del observador.

· Corrientes marinas: se consideró una influencia constante con una velocidad V_c= 0.21 m/s y un ángulo de incidencia β= -36 grados.

· Oleaje: las oscilaciones provocadas por las olas fueron generadas mediante la aproximación lineal de 2do orden del espectro del mar, con los parámetros ζ=0.1 y ω₀=6 rad/seg.

· Adición de ruido blanco a la salida del modelo de 6 GDL con el objetivo de simular una medición real.

· Parámetros iniciales v₀= [0; 0; 0] y Ψ₀= 0°.

SISTEMA EN LAZO ABIERTO

En esta sección se muestran un conjunto de simulaciones con el sistema actuando en lazo abierto, o sea, sin actuar el control de rumbo y por lo tanto sin retroalimentar la salida filtrada del observador que es el objetivo final del trabajo. En este caso el esquema de simulación se muestra en la Figura 2.

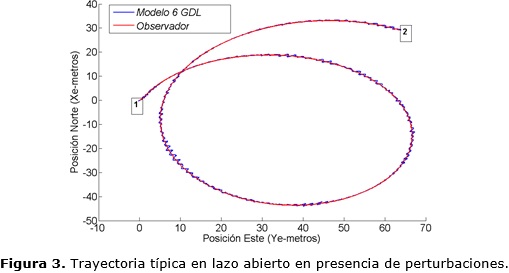
Como en el observador solo se realiza la estimación de la posición en un plano bidimensional x-y, el movimiento en el eje-z no será analizado. Por ello en la Figura 3 se muestra el desplazamiento real y estimado del vehículo en las direcciones Este (Ye) y Norte (Xe). A modo de comparación con el modelo general de 6 GDL utilizado como valores de referencia, se puede observar la trayectoria circular típica del sistema actuando en lazo abierto.

En la Figura 3 las pequeñas oscilaciones en la salida del modelo constituyen el movimiento inducido por las olas y el hecho de que círculo no sea concéntrico sino que se desplace en ambas direcciones está relacionado con la incidencia de las corrientes. Ambos efectos se pueden ver de igual manera en las Figuras 4 y 5 para cada una de las variables de posición (avance, desp. lateral y rumbo) y de velocidad respectivamente.

A pesar de que en las dos gráficas anteriores se muestra una simulación de 50 segundos de duración, no se aprecia la diferencia entre una y otra curva debido a la poca variación entre ellas, estando en casi todos los casos la salida estimada del observador prácticamente superpuesta con la salida del modelo de 6 GDL. La mayor diferencia se puede ver entre las curvas de velocidad en avance y lateral; observándose por ejemplo una convergencia hacia el valor 1.9 en la primera de ellas que representa el valor de velocidad nominal del vehículo y una afectación de las corrientes en la salida del modelo tomada como referencia. En la Tabla 3 se puede apreciar el comportamiento del error de estimación en las tres variables de posición en términos de valor medio y desviación estándar, lo cual brinda una mejor idea del desempeño del observador al contrarrestar en gran medida las oscilaciones del oleaje.

SISTEMA EN LAZO CERRADO

El propósito principal del observador o estimador de estados es reconstruir los componentes del movimiento de BF partiendo de una medición ruidosa. Esto es crucial en los sistemas de control de los VAS debido al movimiento oscilatorio de 1er orden inducido por las olas ^{14 18}. Estas oscilaciones al entrar en el lazo de control, causan desgaste y en algunos casos la ruptura de los actuadores; además de aumentar considerablemente el consumo de energía. Por lo tanto el filtrado de las olas se debe realizar antes de que las señales se utilicen en el sistema de control, entrando al mismo solamente señales suavizadas que contienen la parte que realmente se desea controlar del movimiento. Además de las condiciones de simulación expuestas anteriormente, para cerrar el lazo de control de dirección se incluyen las siguientes:

· Se utilizó un controlador PI-D con ganancias: Kp = 1,2; Kd = 1 y Ki = 0,04.

· Se sometió el sistema a una entrada tipo paso con una amplitud de 0,4 radianes (aprox. 23°) en el valor deseado (Ψ_sp).

· En la realimentación, para la señal de error al controlador de dirección se utilizó la señal filtrada Ψ^{^}.

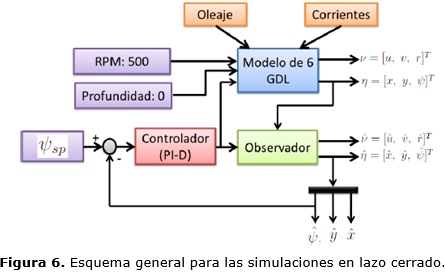
En la estrategia de control utilizada en las simulaciones solamente se toma del observador la señal Ψ^{^} como se muestra en la Figura 6. Resulta necesario resaltar que el observador desarrollado posee la capacidad de proporcionar adicionalmente la estimación de posición y la velocidad del móvil, variables que son de vital importancia en cualquier sistema de guiado que se utilice en implementaciones y pruebas reales futuras.

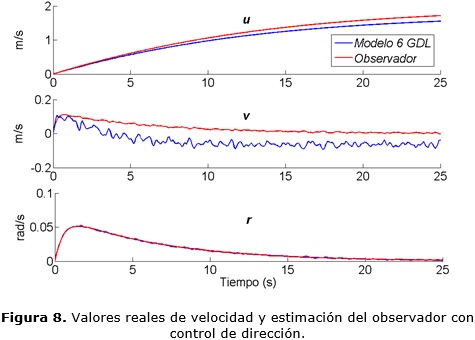
En este caso en las Figuras 7 y 8 se muestra el comportamiento de la posición y la velocidad respectivamente, correspondiente a cada una de las variables de estado del sistema de navegación. Se observa que la medición de rumbo (salida del modelo) y la estimación de rumbo del observador convergen al valor deseado, al igual que la velocidad de avance se estabiliza pues la misma se estabiliza y se mantiene constante. Los valores de razón de cambio de rumbo (r) varían mientras que el rumbo no se ha estabilizado. Se pueden observar además los componentes oscilatorios en la salida del modelo, con distinta medida en cada variable, pero no así en la salida estimada del observador, razón por la cual se debe controlar con estas estimaciones.

Al llevar a cabo un correcto filtrado y realimentar la salida del observador en lugar de la medición ruidosa, se puede contar con estimaciones adecuadas para realizar el control, aun cuando la señal de medición no se encuentre disponible durante pequeños periodos de tiempo ¹⁸. La Figura 9 refleja las diferencias existentes en la señal de mando a la salida del controlador, la azul representa la señal sin observador en la cual se puede apreciar el movimiento oscilatorio inducido por las olas, la curva en rojo muestra la señal de mando controlando con la salida del observador, atenuando esta última considerablemente las vibraciones. Resultado beneficioso para el ahorro de energía y el cuidado de los actuadores.

Finalmente en la Tabla 4 se muestran los datos estadísticos de cada una de estas señales en donde se puede corroborar lo acertado de utilizar en el control la salida del observador en lugar de la medición real, para atenuar los componentes de alta frecuencia presentes en la medición.

 

CONCLUSIONES

 

Los resultados de esta investigación poseen una aplicación práctica y teórica de gran utilidad para el proyecto de autopiloto del vehículo subacuático que desarrolla el GARP, ya que hasta el momento no se cuenta con un algoritmo de navegación definitivo para ser utilizado. El observador pasivo no lineal corrige los efectos indeseables de los principales disturbios medio ambientales utilizando un modelo no lineal del vehículo y aproximaciones lineales de las perturbaciones.

La aplicación de un algoritmo que utilice el modelo del vehículo y los modelos estructurados de las perturbaciones marinas para estimar el movimiento real, facilita la implementación debido a que las otras alternativas con que se puede contar; involucran sensores que poseen un alto precio en el mercado mundial. Debido a la estructura pasiva de este algoritmo presenta ventajas con respecto a otros, al reducir los altos requisitos computacionales y simplificar el método de sintonización de las matrices de ganancias. Mediante las simulaciones realizadas se comprueba el buen desempeño del observador con el sistema operando tanto en lazo abierto como bajo control de dirección.

 

REFERENCIAS

 

1. BALCHEN, J. G. et al. «Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control». IEEE Transaction on Automatic Control. 1983, vol. 28, p. 9.

2. DANTAS, J. L. D. et al. «Study of Autonomous Underwater Vehicle wave disturbance rejection in the diving plane». Proceedings of the Institution of Mechanical Engineering, part M: Journal of Engineering for the Maritime Environment. 2014, vol. 228(2), p. 122-135.

3. BELLETER, Dennis; GALEAZZI, Roberto; FOSSEN, Thor I. «Experimental verification of a global exponential stable nonlinear wave encounter frequency estimator». Ocean Engineering. 2015, vol. 97, p. 48-56.

4. DE LA CRUZ GARCÍA, J. M. et al. «Automática marina: una revisión desde el punto de vista del control». Revista Iberoamericana de Automática e Informática Industrial. 2012, vol. 9, p. 205-218.

5. FOSSEN, Thor I. Handbook of Marine Craft Hydrodynamics and Motion Control. 1ra edición. Editorial John Wiley & Sons, 2011. 596 p.

6. SORENSEN, A. J. Lecture notes on marine control systems. Noruega, Universidad de Ciencia y Tecnología NTNU, 2011.

7. ROSS, A.; FOSSEN, Thor I. «Nonlinear modelling, identification and control of UUVs». En: Advances in Unmanned Marine Vehicles. Gran Bretaña: Peter Peregrinus LTD, 2006. vol. 69. P. 13-42.

8. FOSSEN, Thor I. Marine Control Systems: Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles. 1ra edición. Noruega: Marine Cybernetics AS, 2002. 558 p.

9. TORSETNES, Guttorm. «Nonlinear Control and Observer Design for Dynamic Positioning using Contraction Theory». Director Thor. I. Fossen. Universidad Noruega de Ciencia y Tecnología NTNU, Trondheim, 2004.

10. GARCIA-GARCIA, D. et al. «Wave filtering for heading control of an AUV based on passive observer». Indian Journal of Geo-Marine Sciences (IJGMS). 2012, vol. 41(6), p. 540-549.

11. FALTINSEN, Odd M. Hydrodynamics of High-Speed Marine Vehicles. Johannessen, Anne-Irene (ilust.); Koushan, Keenan (ilust.). 1ra edición. Reino Unido: Universidad de Cambridge, 2006. 476 p.

12. SNAME. Nomenclature for treating the motion of a submerged body through a fluid. Nueva York, Sociedad de Ingenieros y Arquitectos Navales, 1950. Núm. 1-5.

13. VALERIANO-MEDINA, Yunier et al. «Dynamic model for an autonomous underwater vehicle based on experimental data». Mathematical and Computer Modelling of Dynamical Systems: Methods, Tools and Applications in Engineering and Related Sciences. 2013, vol. 19(2), p. 175-200.

14. ROBER, G. D.; ROBERT, A. D. Water wave mechanics for engineers and scientists. 1ra edición. Singapur: World Scientific Publishing Co., 1991. Vol. 2. 371 p.

15. OCHI, M. K. Ocean Waves: The Stochastic Approach. 1ra edición. Reino Unido: Cambridge University Press, 1998. Vol. 6, 332 p.

16. FOSSEN, Thor I.; STRAND, J. Peter. «Passive nonlinear observer design for ships using Lyapunov methods: Full-Scale experiments with a supply vessel». Elsevier Science Ltd. 1999, vol. 35, p. 14.

17. REFSNES, Jon Erling. «Nonlinear Model-Based Control of Slender Body AUVs». Director Asgeir J. Sørensen. Universidad Noruega de Ciencia y Tecnología NTNU, Trondheim, 2007.

18. POTESTA, J. J. «Leveled flight control of an unmanned underwater vehicle operating in a wave induced environment». Universidad de la Florida, Estados Unidos, 2014.

 

 

Recibido: 18 de noviembre de 2014
Aprobado: 13 de febrero de 2015

 

 

Delvis Garcia Garcia, M. Sc. Profesor del Departamento de Automática y Sistemas Computacionales de la facultad de Ingeniería Eléctrica, Universidad Central «Marta Abreu» de Las Villas. Correos electrónicos: [e-mail]; [e-mail]; [e-mail]; [e-mail]