ARTÍCULO ORIGINAL

 

 

Demodulación de señales BFSK con base en la técnica «Early-Late Gate Synchronizer»

 

BFSK waveform Demodulator based upon «Early-Late Gate Shynchronizer»

 

 

Ing. Jorge Alejandro Hernández Torres, Dr. C. Jorge Torres Gómez

Departamento de Telecomunicaciones y Electrónica, CUJAE, La Habana, Cuba.

 

 

---

RESUMEN

El presente artículo introduce un nuevo algoritmo para la demodulación de señales BFSK con parámetros desconocidos, basado en la técnica Early-Late Gate Synchronizer y en el Receptor de Cuadratura. Para su implementación se utiliza la comparación del grado de correlación cruzada entre una sección de la señal y un tono generado localmente en el receptor para la estimación de las transiciones entre símbolos. El desempeño del algoritmo propuesto es verificado mediante simulaciones con señales.

Palabras claves: BFSK, Receptor de Cuadratura, Early-Late Gate.

---

ABSTRACT

This paper addresses a new algorithm for blind demodulation of BFSK signals by means of two techniques; the Early-Late Gate Synchronizer and the Quadratic Receiver. In order to implement the system, the cross-correlation factor between sections of the signal is obtained in order to estimate the transition between consecutives symbols. The performance of the proposed algorithm is described through several simulations with BFSK signals.

Key words: BFSK, Quadratic Receiver, Early-Late Gate.

---

 

 

INTRODUCCIÓN

 

La recepción sin previo acuerdo con el transmisor permite conformar receptores que operen en un rango amplio de parámetros. Debido a variaciones del medio se hace necesario variar la velocidad de transmisión con el objetivo de preservar la probabilidad de bit erróneo en las modulaciones digitales, el receptor debe tener incorporada la capacidad de cambiar por si solo su configuración sin interrumpir la comunicación. Aplicaciones de estos principios se desarrollan hoy en día en las tecnologías de Radio Cognitivo¹ así como en las comunicaciones de quinta generación (5G)² por su marcada heterogeneidad. Este tipo de recepción es útil para conformar un receptor que opere con distintas normas haciendo abstracción de los parámetros de la modulación, por ejemplo, en las comunicaciones bluetooth³ la velocidad de transmisión no es la misma que la utilizada en comunicaciones satelitales⁴ o en las redes corporales (Wireless Body Area Networks)⁵, luego, el detector obtenido usando este esquema no necesita de modificaciones para que opere en una u otra aplicación.

El intervalo de tiempo entre pares de transiciones inter-símbolos (IST: intersymbol transitions) contiene la información del período de símbolo necesaria para obtener la secuencia transmitida. Varios detectores se basan en la estimación de estos instantes, como es el caso de la transformada de onda (Wavelet Transform)⁶. Este método se basa en que las muestras están muy cercanas unas a las otras hasta que ocurre un salto de fase o de frecuencia, en ese instante la magnitud de la transformada devuelve un pico (en el caso de señales PSK) o muestra una desviación constante del valor de magnitud previo (en el caso de señales FSK).

Este método tiene la ventaja de que no es necesario el previo conocimiento de la frecuencia portadora (frequency blind), pero tiene severas limitaciones en su aplicación debido a la necesidad de sobre muestreo⁷, por otra parte su eficiencia se degrada para señales con bajos niveles de SNR (relación señal a ruido)⁸.

Otro método para la estimación del período de símbolo es el que utiliza la transformada rápida inversa de Fourier (IFFT) del espectro de potencia⁹.Con ello se obtiene el valor absoluto de la magnitud del coseno alzado (solo aplica a señales moduladas con pulsos coseno alzado), y el primer mínimo constituye una primera estimación de la duración del símbolo que sirve como punto de partida a una etapa posterior para mejorar la exactitud del resultado. A pesar de la sencillez del método, la obtención del espectro de potencia mediante el promediado de los periodogramas relacionados y el cálculo de la IFFT conllevan a un costo computacional considerable y su aplicación en la demodulación de señales requiere un bloque adicional para la detección de instantes IST.

Los acercamientos más empleados en la estimación del período de símbolo son los basados en la correlación cíclica, estos parten de que la señal sobre muestreada es cicloestacionaria o periódicamente estacionaria con período Ts (es decir, que sus estadísticas no cambian con un desplazamiento de nTs donde n es un entero) y que sus frecuencias cíclicas diferentes de cero son múltiplos enteros de la razón de símbolo⁸. Luego, la estimación del período de símbolo se reduce a la búsqueda de máximos en la amplitud de funciones de correlación cíclica. Este acercamiento tiene la ventaja de que la estimación del período de símbolo obtenida es casi inmune al ruido estacionario. Su desventaja principal reside en un gran costo computacional, dado que este método no estima los instantes IST. Para obtener la secuencia transmitida se debe utilizar un bloque detector adicional al igual que en el caso de los estimadores basados en la IFFT.

Con base en la técnica Early-Late Gate Synchronizer y en el Receptor de Cuadratura (Quadratic Receiver) se propone un nuevo algoritmo para la demodulación de señales BFSK partiendo de la estimación de los instantes IST y del período de símbolo. La idea general es extrapolar técnicas para la estimación de IST en pulsos cuadrados hacia pulsos de radiofrecuencia, lo cual tiene aplicación directa en las señales BFSK.

 

CONFORMACIÓN DEL SISTEMA

 

Esquema General

La técnica Early-Late Gate Synchronizer¹⁰ se basa en la comparación de la componente de directa (CD) acumulada por dos integradores que operan sobre dos secciones de una señal de longitud Ts-d segundos, donde Ts es el período de símbolo, de forma tal que el primer integrador opera desde iTs hasta (i+1)Tsd y el segundo integrador opera desde iTs+d hasta (i+1)Ts, donde i = {0, 1, 2,…}. Si la componente directa acumulada por ambos integradores es diferente, la señal de error ajusta el reloj del sincronizador hasta que el error es cero, obteniendo de esa forma la sincronización con el reloj de los datos recibidos. No obstante, la aplicación directa de la técnica Early-Late Gate Synchronizer en la modulación FSK se imposibilita por la forma de medir la componente directa en las compuertas (Gates) que define el método, pues este se plantea para señales polares o bipolares de las cuales se conoce el período de símbolo. En el caso de la modulación FSK no es realizable una comparación de las componentes directas acumuladas ya que para sinusoides este valor es cero, además, en el marco de las comunicaciones cooperativas no se tiene un conocimiento previo del período de símbolo.

Sin embargo, es posible aplicar la idea de la comparación de dos compuertas de este método de sincronización en conjunto con la detección no coherente para la estimación de la razón de símbolo de señales FSK. Para ello se propone medir el grado de correlación cruzada entre la señal enmarcada por los límites de una ventana y tonos almacenados utilizando el Receptor de Cuadratura (Quadratic Receiver)¹¹.

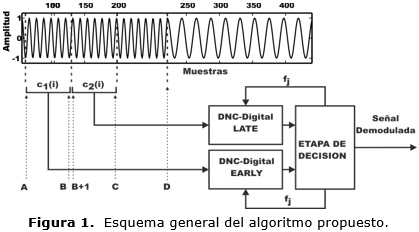
La figura 1 muestra el diagrama de bloques el método propuesto. Las compuertas c₁ y c₂ en forma serie delimitan el intervalo de estudio y su longitud va creciendo muestra a muestra hasta que se detecta que c₂ incurre en el otro símbolo. La idea es establecer una medida que indique cuando ambas compuertas están sobre el mismo símbolo y cuando no. Esta medida se establece por la correlación cruzada entre las señales delimitadas por estas compuertas con el tono almacenado en el receptor de frecuencia f₀, implementado con un receptor de cuadratura.

Si el resultado de ambas compuertas es parecido, entonces el símbolo que transcurre en el intervalo analizado es el mismo. Si por el contrario la compuerta c₂ abarca el símbolo de frecuencia lenta entonces habrá divergencia en el resultado de las correlaciones y se detectará un cambio de símbolo. Esta medida es realizada en ambos bloques, Early y Late, de la figura 1, mediante un umbral la etapa de decisión determina si ambos bloques tienen igual salida o no. La determinación de este umbral se establece con la descripción analítica de esta correlación.

Receptor de Cuadratura

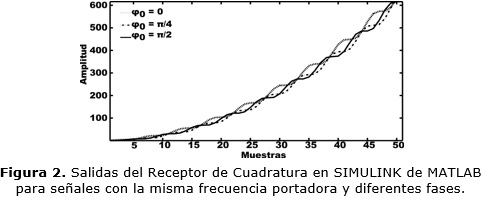
La figura 2 muestra el resultado de aplicar el Receptor de Cuadratura para distintas fases de la señal de entrada. Este tipo de resultado es el que se emplea como entradas de la etapa de decisión en la figura 1. La dependencia de la fase de la señal de arribo se debe a la sustitución del integrador ideal (el cual no es realizable, incluso con circuitos analógicos) por la integración mediante el método de los rectángulos¹² (escogido por su simplicidad) implementado con una estructura IIR (Infinite Impulse Response).

En el método propuesto lo ideal sería un resultado independiente de la fase, puesto que facilitaría la etapa de decisión, los distintos niveles de voltaje se pueden interpretar erróneamente como cambio de símbolo cuando en realidad lo que está cambiando es la fase. Por tanto se hace necesario las operaciones de suma y elevación al cuadrado de las salidas de los integradores en ambas ramas del Receptor de Cuadratura (Quadratic Receiver) por otras operaciones que conlleven a una salida independiente de la fase y que a la vez permitan distinguir un símbolo de otro. Para ello se debe realizar un análisis descriptivo de este receptor hasta la salida del integrador en cada rama.

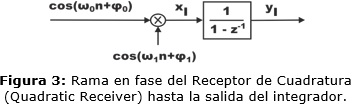
La figura 3 muestra en bloques la operación de multiplicación y acumulación del Receptor de Cuadratura. A partir de este esquema se obtienen las ecuaciones de y_I y x_I como se indican en (1) y (2). Los homólogos de (1) y (2) se muestran en las ecuaciones (3) y (4) respectivamente para la rama en cuadratura [8]. En este caso ω₀=(2πf₀)/fm y ω₁=(2πf₁)/fm se refieren a la frecuencia digital, donde fm representa la frecuencia de muestreo.

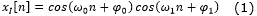
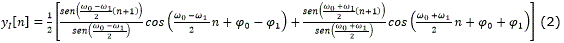
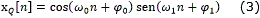
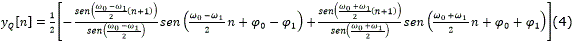
El clásico receptor de cuadratura realiza la operación y_I² [n]+y_Q² [n] para eliminar el efecto de las fases φ₀ y φ₁, no obstante la figura 2 muestra que tal efecto no es logrado. En este artículo se sustituye la operación antes indicada por otra que cancele totalmente el efecto de la fase.

Supresión del efecto de la fase

Las funciones trigonométricas sen(x) y cos(x) tienen la característica de que su derivada retorna a las mismas funciones trigonométricas. Ya que las salidas de los integradores de la rama en fase y en cuadratura están compuestas por senos y cosenos, como se indica en (2) y (4), cabría considerar que mediante derivación se pueden obtener nuevas ecuaciones linealmente independientes que permitan cancelar el efecto de la fase φ₀ de la señal de entrada. Esta derivación se implementa por medio de un sistema diferenciador de primer orden, y'_I [n]=y_I [n]- y_I [n-1], y su resultado se indica en (5) y (6)¹³.

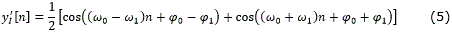
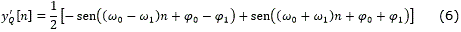
Partiendo de las ecuaciones (2), (4), (5) y (6) se obtiene la independencia con la fase de la señal de entrada como se muestra en (7)¹³.

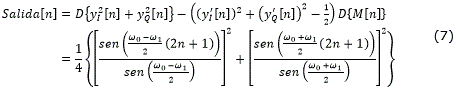
Donde el operador D{·} representa la operación de diezmado con una factor de 2 (es decir, D{A[n]} es equivalente a extraer las muestras pares del arreglo A[n]) y el arreglo M[n] está definido por:

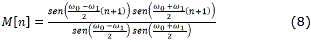
Para el caso en que la frecuencia del oscilador local ω₁ coincida con la frecuencia portadora del símbolo actual de la señal BFSK ω₀, la salida del sistema se obtiene mediante el límite como se muestra en (9). Esta salida es la que se obtiene luego de implementarse la relación (7) con y_I [n] e y_Q [n], y lo más importante es que representa una salida totalmente independiente de la fase de la señal de entrada, es decir, ambas entradas al bloque de decisión en la figura 1 serán idénticas toda vez que ambas compuertas se encuentren sobre el mismo tono.

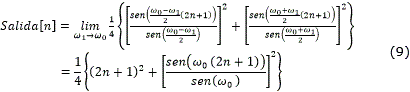
Determinación del umbral de detección

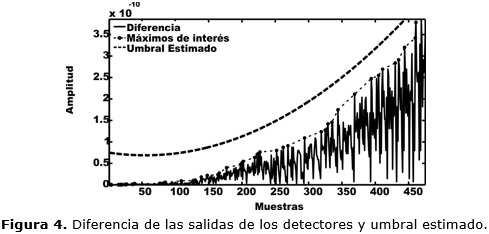
En la figura 4 se muestra la diferencia de las salidas de ambos detectores cuando las frecuencias de sus osciladores locales son cercanas a la frecuencia del símbolo (en el caso de la figura 3, f₀=882Hz). Debido a que las salidas no son exactamente iguales aunque casi cero, es necesario establecer un umbral a partir de varias ejecuciones del algoritmo propuesto. La detección del cambio de un símbolo a otro se resume entonces a detectar el instante a partir del cual el valor absoluto de la diferencia de los grados de correlación es mayor que el umbral.

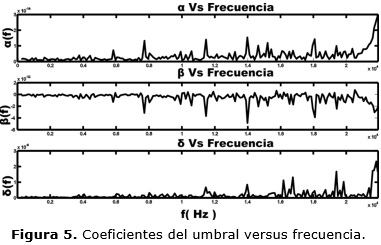
Partiendo del resultado obtenido en la figura 3 se escoge la función cuadrática de la forma αx²+βx+δ como umbral genérico. Es necesario entonces realizar un análisis de las curvas de los coeficientes α, β y δ del umbral versus frecuencia.

Las curvas de los coeficientes obtenidas a partir de la ejecución del algoritmo propuesto para un rango de frecuencias desde 200Hz hasta 22kHz se muestran en la figura 5. Para α, β y δ se escogieron los valores máximos de sus respectivas curvas, debido a las características intrínsecas de las mismas.

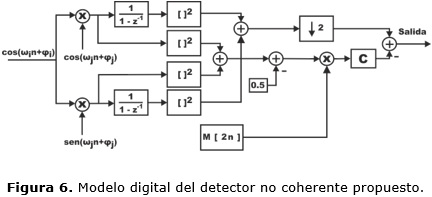
Modelo digital del detector propuesto

En base al resultado alcanzado en (7) se obtiene el modelo digital del detector, mostrado en la figura 6.

Dado que el proceso de acumulación se cancela con el proceso de derivación, no se incluyen los elementos diferenciadores en el esquema de la figura 6. Por otro lado, en el esquema se puede apreciar que el arreglo generado localmente M[n] está evaluado en 2n, esto es debido a que M[2n]equivale a diezmar a M[n] manteniendo su longitud. El bloque marcado con la letra C es el encargado de realizar la limitación de la longitud de los arreglos para realizar la resta muestra a muestra con el arreglo a la salida del diezmador.

 

RESULTADOS

 

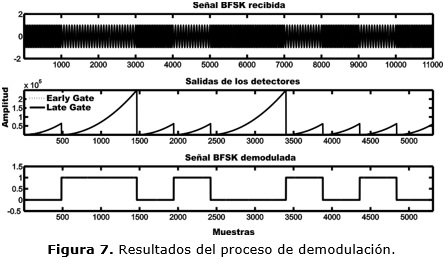
Aplicando el criterio de decisión basado en la comparación con un umbral se obtienen los resultados mostrados en la figura 7 para una señal BFSK de frecuencias portadoras: f₀=970.2 Hz y f₁=617.4 Hz utilizando una frecuencia de muestreo de 44100 Hz.

El desempeño del algoritmo propuesto es independiente de la frecuencia con la cual se inicia el proceso pues es capaz de reconocer este error y cambiar a la frecuencia a la indicada. Es aconsejable fijar el tamaño inicial de las ventanas que limitan a las secciones de la señal a un valor pequeño, por ejemplo, media oscilación del tono de mayor frecuencia, con el fin de no perder algún cambio de símbolo debido a la resolución inicial.

 

CONCLUSIONES

 

En el presente artículo se desarrolló un nuevo detector de señales BFSK con base en el Detector de Quadratura y la técnica de sincronismo Early-Late Gate. Esto como resultados de una extrapolación de técnicas para pulsos cuadrados a pulsos de radiofrecuencia. La ventaja de emplear operaciones de correlación es que estas maximizan la relación señal a ruido a la salida, brindando así una característica adicional. Los resultados de la simulación muestran que la estimación de los cambios de símbolo es bastante exacta producto de tomar un umbral en el orden de 10^-10.El algoritmo propuesto resulta sencillo, fácil de implementar y es atractivo en el contexto de las comunicaciones no cooperativas. El algoritmo propuesto permite hacer su extensión a señales FSK no binarias con la duplicación de los correladores.

 

REFERENCIAS

 

1. Asadi, H., Volos,H., Marefat, M. M., Bose, T.: «Metacognitive Radio Engine Design and Standardization,» IEEE Journal on Selected Areas in Communications, vol. 33, no. 4, pp. 711-724, Apr. 2015.

2. Wang, N., Hossain, E., Bhargava, V. K.: «Backhauling 5G small cells: A radio resource management perspective,» IEEE Wireless Communications, vol. 22, no. 5, pp. 41-49, Oct. 2015.

3. Vinagre Diaz, J. J., Rodriguez Gonzalez, A. B., Wilby, M. R.: «Bluetooth Traffic Monitoring Systems for Travel Time Estimation on Freeways,» IEEE Transactions on Intelligent Transportation Systems, vol. 17, no. 1, pp. 123-132, Jan. 2016.

4. Maleki, S., Chatzinotas, S., Evans, B., Liolis, J. Grotz, K., Vanelli-Coralli, A., Chuberre, N.: «Cognitive spectrum utilization in Ka band multibeam satellite communications,» IEEE Communications Magazine, vol. 53, no. 3, pp. 24-29, Mar. 2015.

5. Cavallari, R., Martelli, F., Rosini, R., Buratti, C., Verdone, R.: «A Survey on Wireless Body Area Networks: Technologies and Design Challenges,» IEEE Communications Surveys Tutorials, vol. 16, no. 3, pp. 1635-1657, Third 2014.

6. Lilly, J. M., Olhede, S. C.: «On the Analytic Wavelet Transform,» Information Theory, IEEE Transactions on, vol. 56, no. 8, pp. 4135-4156, Aug. 2010.

7. Barnes, W. J., LaSorte, N., Refai, H., Yeary, M. B.: «Symbol rate classification of PSK/QAM signals using direct frequency estimators,» in IEEE Instrumentation and Measurement Technology Conference, 2009. I2MTC '09, 2009, pp. 943-946.

8. Tang, S.: «Fast Algorithm for Symbol Rate Estimation,» IEICE transactions on communications, vol. 88, no. 4, p. 1649-, 2005.

9. Xu, H., Zhou, Y., Huang, Z.: «Blind Roll-Off Factor and Symbol Rate Estimation Using IFFT and Least Squares Estimator,» in International Conference on Wireless Communications, Networking and Mobile Computing, 2007. WiCom 2007, 2007, pp. 1052-1055.

10. Sklar, B.: Digital Communications, Fundamentals and Applications, Second. New Jersey: Prentice Hall, 2001.

11. Haykin, S.: Communication Systems, 4th Edition. John Wiley & Sons, 2001.

12. Philip, J. D., Rabinowitz, P.: Methods of Numerical Integration: Second Edition, Second Edition edition. Dover Publications, 2007.

13. Hernandez Torres, J. A.: «Demodulación de señales BFSK con base en la técnica `Early - Late Gate Circuit',» Tesis de Doctorado en Telecomunicaciones y Electrónica, CUJAE, La Habana, 2013.

 

 

Recibido:13 de noviembre de 2014
Aprobado: 6 de mayo de 2015

 

 

Jorge Torres Gómez, Departamento de Telecomunicaciones y Electrónica, CUJAE, La Habana, Cuba. E-mails: [e-mail].