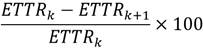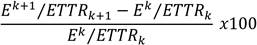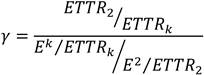1. INTRODUCCIÓN
En la actualidad, con el incremento del tráfico de comunicación móvil, la utilización de los recursos disponibles del espectro se ha convertido en el centro de atención. El espectro radioeléctrico representa un recurso natural que ha sido sistemáticamente inutilizado debido a las ineficientes políticas de asignación fija de las bandas de frecuencias. Las técnicas de Acceso Dinámico al Espectro han sido desarrolladas en redes radio cognitivas, tanto para resolver la situación del acceso a la restringida porción libre del espectro, como para optimizar la eficiencia en el uso de las bandas reservadas [1].
En las redes radio cognitivas (RC) coexisten dos tipos de usuario: los usuarios primarios (UP), que son aquellos que poseen licencia para operar en ciertas bandas del espectro y los usuarios secundarios (US) o usuarios cognitivos que no poseen licencia de operación en estas bandas. Cada US puede estar equipado con uno o más radios capaces de captar la información del espectro y detectar porciones que no estén ocupadas por los UP. Al identificar las porciones libres del espectro los US pueden hacer un uso oportunista de las mismas. Para establecer un enlace de comunicación, dos US deben encontrarse en un canal común libre e intercambiar información de señalización, este proceso se denomina Rendezvous (reunión, encuentro) y es imprescindible para el funcionamiento de estas redes [2,3]. Los canales disponibles para cada usuario varían con el tiempo y con la posición geográfica del mismo; por ello para dos US, ubicados en zonas geográficas distantes, el conjunto de canales libres que detectan podría no coincidir [4]. De acuerdo a la disponibilidad del espectro percibida por los US que intentan establecer el Rendezvous, las redes RC se clasifican en dos modelos fundamentales: el modelo Simétrico, en el cual diferentes US perciben igual disponibilidad de canales y el modelo Asimétrico en caso contrario. En este trabajo se reconoce un modelo Ideal como un caso particular del modelo Simétrico en el cual todos los canales están disponibles para los US.
Los algoritmos de Rendezvous ciego no necesitan de sincronismo entre los US y se basan fundamentalmente en las técnicas de salto de canal, en las que cada US sigue una secuencia de saltos hasta lograr el Rendezvous con el otro US con que se desea comunicar. La clave de esta técnica radica en el algoritmo empleado para generar el orden en que son visitados los canales [4]. Aunque algunos algoritmos de Rendezvous ciego utilizan sincronización en el tiempo, la heterogeneidad de la red dificulta sincronizar todos los US.
Debido a los problemas asociados a la sincronización se han desarrollado algoritmos que no requieren de la misma. Uno de los más representativos es propuesto en [5]. Este algoritmo solo garantiza el Rendezvous en modelos simétricos donde todos los usuarios tienen igual disponibilidad del espectro. Atendiendo a esta limitante se propone en [6] el algoritmo ACH (Asynchronous Channel Hopping) que garantiza el Rendezvous tanto en sistemas simétricos como asimétricos, asumiendo que existen dos roles en el proceso, transmisor (Tx) y receptor (Rx), que separadamente generan secuencias de salto de canal (SC) y solo se puede efectuar el Rendezvous en un sentido, de Tx a Rx. Algunos algoritmos basados en esta idea utilizan además un método conocido como camino en anillo (RW, Ring-Walk) [7], donde cada canal es representado por un vértice en un anillo y los US visitan los vértices (canales) con diferentes velocidades y el Rendezvous se garantiza porque los usuarios que más rápido recorren el anillo alcanzan a los más lentos [4]. Otras investigaciones [5,8-12] llevaron al desarrollo de varios algoritmos que también garantizan el Rendezvous tanto en modelos simétricos como asimétricos, lo que resulta de gran importancia al evaluar su desempeño.
El parámetro que mejor describe el desempeño de los algoritmos de Rendezvous es el tiempo para Rendezvous (TTR, Time To Rendezvous). Se define el TTR como el número de ranuras de tiempo necesarias para que dos US logren el Rendezvous una vez que hayan comenzado los saltos de canal, considerando que una ranura representa el tiempo máximo establecido para un único intento de encuentro entre los US. Frecuentemente son empleadas dos métricas diferentes para evaluar el TTR: valor esperado o promedio del TTR (ETTR, Expected TTR) y valor máximo TTR (MTTR, Maximum TTR) [13].
La mayor parte de los algoritmos reportados implícitamente consideran que cada US está equipado con un único radio, debido a que los algoritmos generan una única salida (canal en el cual intentar el Rendezvous) en cada ranura de tiempo. Si en lugar de utilizar un solo radio los algoritmos se implementan con múltiples radios, se puede reducir el TTR porque es posible intentar el Rendezvous en más de un canal simultáneamente aprovechando en mayor medida cada ranura de tiempo [2]. Sin embargo, el aumento del número de radios impone retos adicionales asociados al consumo de energía y a la complejidad de los dispositivos.
En este trabajo se analiza la relación de compromiso que se establece entre la disminución del TTR mediante el empleo de múltiples radios y el consumo de energía durante el proceso de Rendezvous. Aunque existen otros trabajos [2,13,14] donde se ha analizado el comportamiento del tiempo de Rendezvous e incluso se han realizado comparaciones entre algoritmos atendiendo a esta métrica, no se ha profundizado en el costo energético asociado a la reducción de dicho tiempo mediante el empleo de múltiples radios. La principal novedad en este trabajo radica en que la comparación que se realiza entre los algoritmos de Rendezvous también toma en consideración el desempeño de dichos algoritmos atendiendo al factor energético. Los resultados obtenidos mediante simulación ilustran que el aumento del número de radios resulta en un aumento en el costo energético por ranura de tiempo, aunque este comportamiento no se manifiesta de igual manera en ambos algoritmos estudiados debido a las estrategias que utilizan para dividir y asignar roles a los radios. Con el mismo consumo energético debido al aumento del número de radios, el algoritmo G-FDCH-CS (Generalization Full Diversity Channel Hopping Common Sequence) logra mejores beneficios en el ETTR que el RPS (Role Based Parallel Sequence), lo cual puede ser aplicado en el diseño e implementación futura de redes radio cognitivas en Cuba y el resto del mundo.
2. CONSIDERACIONES ENERGÉTICAS DE LAS REDES RC
El creciente desarrollo de las técnicas de RC, para encontrar y usar el espectro disponible para redes inalámbricas en equipos móviles, ha resultado en una búsqueda por minimizar el consumo energético de los dispositivos que emplean dicha técnica. Los autores en [15] describen las influencias positivas y negativas, en cuanto a consumo energético, asociadas al empleo de las técnicas de RC.
Mirando desde un ángulo positivo, las técnicas de RC reducen la energía consumida para el establecimiento de la conexión al encontrar las porciones libres del espectro, que lógicamente se encuentran menos congestionadas. Esto puede facilitar el establecimiento de la comunicación con menor probabilidad de interferencia del medio, lo que resulta otro factor que requiere de un consumo energético adicional para los dispositivos móviles. Mayor interferencia del medio resulta típicamente en un aumento del número de colisiones y en el tiempo invertido en responder a este problema, ya sea esperando un tiempo aleatorio o apartándose. Basados en esto, los autores en [15] realizan comparaciones entre un radio cognitivo que examina una porción del espectro para escoger un canal y establecer comunicación, y un radio convencional fija en un canal dentro de este mismo espectro para transmitir la misma información, demostrando que el dispositivo cognitivo es energéticamente más eficiente y capaz de ahorrar de un 20% a un 40% de la energía consumida por un radio convencional. Por otra parte, acciones como el análisis del espectro para detectar las porciones libres, los posibles saltos entre los canales y el proceso de señalización hasta lograr establecer el Rendezvous, se traducen en un consumo intensivo de energía y pueden resultar en una disminución del tiempo de vida de la batería de los dispositivos móviles (tabletas, laptops, teléfonos inteligentes, sensores inalámbricos).
En el presente trabajo se analiza el consumo asociado únicamente al proceso de señalización entre los usuarios intentando establecer el Rendezvous, utilizando el mecanismo de señalización RTS/CTS (Request to Send/Clear to Send) definido en el estándar IEEE 802.11. De esta forma cada usuario con cada uno de sus radios acumula paulatinamente tiempos de transmisión y recepción de paquetes RTS o CTS así como tiempos de espera o de inactividad en dependencia del rol que desempeñan los radios en la comunicación. Una vez logrado el Rendezvous, la energía invertida en cada una de estas funciones será el producto de la potencia que consume el radio en realizarla, multiplicado por el tiempo total que estuvo realizándola. La Tabla 1 muestra los valores de consumo de potencia en las diferentes funciones de comunicación de dos radios ampliamente difundidos.
Los radios cognitivos se encargan del proceso de señalización y son los componentes de mayor consumo energético dentro de un dispositivo típico de rastreo del espectro. Además trabajan en distintos modos de operación que se relacionan con las funciones que realizan y pueden resumirse en: transmisión, recepción e inactivo. La potencia que se consume durante el modo inactivo es muy pequeña en comparación con la del resto de los modos de operación y no representa una contribución significativa al cálculo de la energía. Los intervalos de tiempo durante los cuales el radio cognitivo se encuentra en espera de un paquete o simplemente escuchando el canal, podrían clasificarse como intervalos de tiempo inactivo del dispositivo [18].
Los radios CC2420 y CC1000 poseen valores típicos de potencias en los tres modos de operación. Atendiendo a que el objetivo del presente trabajo es evaluar algoritmos de Rendezvous con múltiples radios se considera que los US están equipados con más de un radio. Cada radio emplea potencias de transmisión, recepción e inactividad similares a las que emplean los radios descritos en la Tabla 1.
3. MODELO DEL SISTEMA
Se considera una red RC formada por M usuarios secundarios ubicados en la misma área geográfica. Desde el punto de vista de los US, el espectro se divide en N canales, A u representa el conjunto de canales disponibles para el usuario secundario u, se considera que no existe solapamiento entre canales adyacentes y que no están siendo utilizados por los UP en ningún momento (A u =N). Los US identifican de manera única cada uno de los canales de la red usando las etiquetas 0,1,2,…,N-1. La comunicación es dividida en ranuras de tiempo de duración fija y cada US está equipado con k ≥ 2 radios que son identificados como 2,3,…,k. Sea S u t = {S u t,1 , S u t,2 , …, S u t,k } los canales visitados por el US u en la ranura de tiempo t, donde S u t,i representa el canal visitado por el US u con el radio i en la ranura de tiempo t.
Sea τ el tiempo necesario para intercambiar la información de señalización. Debido a que los US pueden no estar sincronizados se considera 2τ como la duración de una ranura de tiempo para asegurar que el solapado de dos ranuras cualquiera de tiempo sea suficiente para completar el proceso de Rendezvous [19]. Esto equivale a considerar que las ranuras de tiempo de los US están alineadas, aunque cada uno puede comenzar su secuencia de salto de canal en ranuras de tiempo diferentes [20]. Se considera que los US emplean los algoritmos RPS [21] y el algoritmo G-FDCH-CS [22] debido a que son algoritmos que están diseñados para ser empleados con múltiples radios por usuario además de presentar buen desempeño en términos de ETTR.
Para el cálculo de la energía se tiene en cuenta solamente el proceso de señalización, mediante el envío de paquetes RTS/CTS, obviando los consumos asociados a los saltos entre los canales y al reconocimiento del espectro. Se considera que los radios que realizan las funciones de recepción desde el comienzo de las ranuras de tiempo se encuentran en un estado inactivo mientras los radios de transmisión inician transmitiendo paquetes RTS, y luego pasan a un estado de espera de paquetes CTS. En caso de que un radio receptor de un usuario coincida con el transmisor de otro, el receptor inicia la recepción y cuando termina de recibir el paquete RTS comienza a transmitir el paquete CTS, de esta forma el transmisor pasa a recibir este paquete hasta completar el proceso de señalización. Se calculan los tiempos empleados por cada radio cognitivo de cada usuario para transmitir paquetes RTS, recibir paquetes RTS, esperar paquetes CTS o RTS (estado inactivo), transmitir paquetes CTS y recibir paquetes CTS.
Sea Ei es la energía consumida por el radio i durante el proceso de señalización de manera tal que:
E i =E T +E R +E Inact , (1)
siendo, E T =∑ ∀j P Tj *t Tj , j=RTS,CTS la energía empleada para la transmisión de RST/CTS. E R =∑ ∀j P Rj *t Rj , j=RTS,CTS la energía empleada en la recepción y E Inact =P Inact *t Inact la energía en el estado inactivo. P Tj y P Rj denotan la potencia empleada en la transmisión y recepción de mensajes (RTS y CTS) respectivamente. Mientras que t Tj y t Rj el tiempo empleado en la transmisión y recepción respectivamente.
4. ALGORITMOS DE RENDEZVOUS EMPLEADOS
Numerosos algoritmos de Rendezvous han sido propuestos para resolver el Rendezvous ciego. En [21] los autores proponen el algoritmo RPS el cual está generalizado para que se implemente con múltiples radios. La idea básica de dicho algoritmo es dividir los radios que posee el US en dos grupos que interpretan roles diferentes. Un grupo formado por un único radio, nombrado radio dedicado que realiza la función de receptor y otro grupo formado por el resto de los radios, nombrados radios generales que funcionan como transmisores. Esta asignación de roles hace que, siempre que un US esté equipado con dos o más radios solo uno de ellos tendrá el rol de receptor mientras el resto serán marcados como transmisores. Los US saltan con los radios generales mientras permanecen fijos con su radio dedicado en un canal. El Rendezvous se espera que ocurra entre los radios generales de un US con el dedicado del otro. El pseudocódigo del RPS se muestra en el Algoritmo 1. Los k-1 radios generales saltan a partir de una semilla inicial l elegida aleatoriamente (línea 4 del pseudocódigo) y de manera independiente por cada US, mientras que el radio dedicado permanece en el mismo canal durante ⌈P/(k-1)⌉ ranuras de tiempo (línea 13 del pseudocódigo).
El valor h elegido aleatoriamente (línea 4) determina el tamaño del salto entre los radios generales. Por ejemplo en una red con N=7 canales un US con k=3 tres radios que haya elegido l=2 como semilla y h=3, en la primera ranura de tiempo visitará los canales: S1 u={1,4,6}. Nótese que los radios generales visitan los canales 2 y 5 siendo la distancia (en número de canales) entre ellos igual a h=3. En la segunda ranura de tiempo los canales visitados son: S2 u={0,3,6}. Comparando los canales visitados en cada ranura de tiempo se aprecia que cada radio general (transmisor) recorre los canales en orden descendente (línea 7) y que el canal dedicado (receptor) se mantiene en el mismo canal (línea 13) varias ranuras de tiempo (tal y como se expresó anteriormente). Si alguno de los canales generados no se encuentra disponible para el US entonces se emplea la operación de reemplazo de las líneas 10-11 o 14-15 para sustituirlo por uno disponible.
Una vez que los US han seleccionado los canales con cada uno de sus radios, los radios transmisores envían un mensaje RTS (línea 17) mientras que el radio dedicado espera por el arribo de un mensaje CTS. Al finalizar la ranura de tiempo si el US recibió en CTS significa que se completó el Rendezvous. Este proceso de intercambio de mensajes RTS/CTS así como la capacidad del algoritmo de alcanzar el Rendezvous en un corto tiempo define la energía empleada en este proceso.
En [2] los autores proponen dos variantes del algoritmo FDCH (Full Diversity Channel Hopping) con el cual el Rendezvous puede ocurrir en cualquiera de los canales disponibles del US (diversidad máxima). Las variantes propuestas tienen la idea fundamental de representar los canales como T nodos de un anillo circular y con el requisito de que el total de nodos en el anillo (T≥N) sea impar de forma tal que:
En la variante FDCH-RB (Full Diversity Channel Hopping-Role Based) los US toman, cada uno, un rol en la comunicación, transmisor o receptor. Sin embargo, el FDCH-CS (Full Diversity Channel Hopping-Common Strategy), por su parte, permite que en cada ranura de tiempo cada US intente el Rendezvous con ambos radios simultáneamente. Esta última variante fue generalizada (G-FDCH-CS) para implementarse con múltiples (más de dos) radios en [22] utilizando la estrategia de secuencia paralela propuesta en [21].
El Algoritmo 2a) muestra el pseudocódigo del G-FDCH-CS. La idea de este algoritmo es dividir los radios a la mitad si el número total es par, mientras, si el número de radios es impar habrá un radio más con el rol de transmisor que de receptor (líneas 4 y 7 en Algoritmo 2a)). De esta forma, al aumentar el número de radios de par a impar, el algoritmo reconoce otro radio transmisor, pero cuando se aumenta el número de radios de impar a par el algoritmo reconoce un radio receptor más. Los canales visitados se basan en las secuencias de transmisión y recepción mostradas en el Algoritmo 2b) y 2c) respectivamente. La secuencia de transmisión recorre los canales en orden descendente mientras que la secuencia de recepción lo hace en orden ascendente (línea 2 en el Algoritmo 2b) y c)). En ambos casos se emplea una operación de reemplazo que sustituye los canales no disponibles por algunos de los disponibles (Algoritmo 2d)). El canal inicial donde los radios transmisores y receptores comienzan sus secuencias de salto es elegido a partir de una semilla aleatoria (línea 7 en el Algoritmo 2 a)). Por ejemplo, en una red con N=7 canales un US con k=3 tres radios que haya elegido como semilla para comenzar el Rendezvous S T (0)=S R (0)=2 visita en la primera ranura de tiempo los canales: S1 u={6,5,3} mientras que en la siguiente ranura de tiempo los canales S2 u={4,3,4}. A partir del ejemplo anterior se verifica que los ⌈k/2⌉ de menor orden son marcados como transmisores y visitan los canales en orden descendente. Mientas que el resto de los radios, funcionan como receptores y visitan los canales en orden ascendente.
De igual forma que para el algoritmo RPS, se considera que una vez que el US visita los canales correspondientes implementa un mecanismo de señalización RTS/CTS (líneas 16-19 en Algoritmo 2a)). Este mecanismo RTS y CTS es idéntico para ambos algoritmos y permite evaluarlos de manera justa atendiendo al consumo energético durante el proceso de Rendezvous.
5. RESULTADOS Y DISCUSIÓN
Para la simulación de los algoritmos G-FDCH-CS y RPS se programan los simuladores de eventos discretos como funciones del software MATLAB. Dichos simuladores permiten variar la cantidad de radios empleados (k) por los US. Se realizan 105 corridas de cada escenario y se estima la media aritmética de los resultados obtenidos de TTR y consumo energético. Para garantizar que la cantidad de simulaciones utilizadas fueran suficientes se calcula el error en cada una de las estimaciones logrando que el mismo fuera menor que el cinco por ciento del valor de la media aritmética.
La red RC simulada posee M=2 US y el número de radios de cada uno de ellos se aumenta de uno en uno desde 2 hasta 10. El número de canales de la red es N=25 ya que es suficiente con este valor para observar y evaluar el comportamiento de los algoritmos incluso cuando se trabaja con el número máximo de radios considerado. Teniendo en cuenta un escenario ideal, todos los canales están disponibles para los US.
Debido a que cada US posee múltiples radios, cada uno puede visitar varios canales en una misma ranura de tiempo. En cada ranura de tiempo los US utilizan un mecanismo de señalización RTS/CTS con todos sus radios en el canal que se seleccionó empleando los algoritmos de Rendezvous descritos en el epígrafe anterior. La longitud de los paquetes RTS y CTS es de 5bits y la razón de Tx se considera que es de 1kbps en todos los escenarios. De esta forma la duración de cada paquete sería entonces t RTS = t CTS = 5/R Tx = 5ms. El tiempo necesario para intercambiar la información de señalización (τ) sería la duración de un paquete RTS más la duración de un paquete CTS, en otras palabras 2 × 5ms = 10ms. Finalmente, la duración de una ranura de tiempo es 20ms, lo que se corresponde con lo acordado en el estándar IEEE 802.22 [23].
Son evaluados tres escenarios atendiendo a los valores de potencias consumidas por los radios de los US. Un primer escenario con iguales potencias de transmisión y de recepción utilizando valores típicos de radios cognitivos. Un segundo escenario con potencia de recepción mayor que de transmisión y un tercer escenario con potencia de transmisión mayor que de recepción. Los valores de potencia en cada uno de estos escenarios se muestran en la Tabla 2.
Tabla 2 Especificaciones de los escenarios simulados
| Escenarios | Valores de las potencias consumidas | |||
|---|---|---|---|---|
| No. | Característica | Pt | Pr | Pinact |
| 1 | Pt=Pr | 60mW | 60 µW | |
| 2 | Pr>Pt | Pt del radio CC2420 (57mW) | Pr del radio CC2420 (63mW) | Pinact del radio CC2420 (60µW) |
| 3 | Pt>Pr | Pt del radio CC1000 (75mW) | Pr del radio CC1000 (36mW) | Pinact del radio CC1000 (100µW) |
5.1 RESULTADOS EN TÉRMINOS DE ETTR Y MTTR
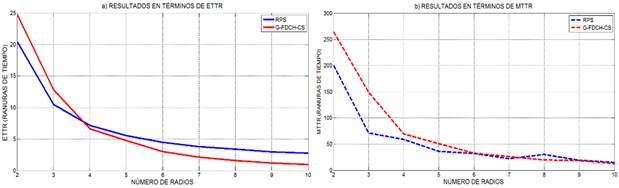
Los resultados de la simulación en términos de ETTR y MTTR se muestran en la Figura 1 a) y b) respectivamente. Tanto el ETTR y el MTTR se expresan en ranuras de tiempo y el número de radios en unidades (radios).
Los resultados mostrados en la Figura 1 se corresponden con lo demostrado por el autor en [22]: al aumentar el número de radios el ETTR y el MTTR disminuyen en los algoritmos simulados, aumentando la probabilidad de Rendezvous. Sin embargo, en la medida que aumenta el número de radios la mejora en términos de ETTR y MTTR es menos significativa.
Sea ETTR k el ETTR con k radios, la Figura 2 muestra la relación:
lo que se traduce en el por ciento de mejora de los algoritmos G-FDCH y RPS al incrementar en una unidad el número de radios en términos de ETTR.
El por ciento de mejora del ETTR es cada vez menor al incrementar el número de radios. En ambos algoritmos al utilizar tres radios la mejora es de aproximadamente 50% con respecto a dos radios, o sea el Rendezvous ocurre en la mitad del tiempo, pero al utilizar nueve radios la mejora con respecto a ocho radios no se aleja demasiado del 20%. Este índice de mejora determina la relación desempeño-costo, por lo que se utiliza para analizar si es conveniente usar un dispositivo de radio más o no.
5.2. RESULTADOS EN TÉRMINOS DE COSTO ENERGÉTICO
Para evaluar y comparar el comportamiento de los algoritmos en cuanto al costo energético asociado al proceso de señalización se empela una métrica que brinda una medida de qué costo energético se requiere por ranura de tiempo para establecer el Rendezvous. La energía requerida por ranura de tiempo hasta establecer el Rendezvous puede calcularse como:
Energía/ETTR =E k /ETTR (4)
siendo E k =∑ k i=1 E i la energía empleada por un US con k radios para establecer el Rendezvous y Ei la energía empleada por el radio i tal y como expresa la ecuación (1).
5.2.1. RESULTADOS EN EL ESCENARIO NÚMERO 1
En este primer escenario son consideradas iguales potencias de transmisión y recepción para los radios (ver Tabla 2). La Figura 3 muestra los resultados de la simulación en términos de costo energético por ranura de tiempo para este escenario.

Figura 3 Resultados de la simulación del escenario número uno en términos de costo energético por ranura de tiempo.
Como se observa en la Figura 3, en ambos algoritmos con el aumento del número de radios ocurre un incremento en el consumo energético por ranura de tiempo necesario para el funcionamiento simultáneo de estos dispositivos hasta completar el Rendezvous. Sin embargo, en el caso del RPS, el costo energético aumenta de manera casi lineal mientras en el G-FDCH-CS el comportamiento es similar a una escalera. Los incrementos más representativos en el G-FDCH-CS ocurren cuando el número de radios pasa de ser par a impar, estas diferencias entre los algoritmos se deben a la manera en que los radios son divididos para desempeñar los diferentes roles.
La potencia que consumen los radios inactivos es casi despreciable con respecto a las potencias de transmisión y recepción. En las simulaciones se consideró que los radios transmisores comienzan la ranura de tiempo transmitiendo paquetes RTS y los receptores, en estado inactivo hasta que coincidan con un transmisor en el mismo canal en la misma ranura de tiempo. A partir de las condiciones se puede deducir que los radios con el rol de transmisores representan mayor costo energético que los radios con el rol de receptores.
En el algoritmo RPS un solo radio realiza la función de receptor mientras que el resto funcionan como transmisores, por lo tanto el incremento del costo energético es lineal. Por su parte el G-FDCH-CS divide los radios a la mitad si el número total es par, mientras, si el número de radios es impar habrá un radio más con el rol de transmisor que de receptor. En este algoritmo, al aumentar el número de radios de par a impar, se considera otro radio transmisor, el cual representa un costo energético significativo. Sin embargo, cuando se aumenta el número de radios de impar a par se considera un radio receptor más y este mientras esté inactivo (lo que ocurre la mayor parte del tiempo) no representa un costo significativo. Estas singularidades de los algoritmos influyen en el comportamiento de los mismos estableciendo notables diferencias. Por medio de la Figura 3 se puede concluir que el G-FDCH-CS presenta mejor desempeño que el RPS en cuanto a costo energético por ranura de tiempo.
En el algoritmo G-FDCH-CS, cuando el número de radios es par y se incrementa en uno, el factor energético no se afecta significativamente, sin embargo, este incremento en el número de radios sí representa una mejora notable en el ETTR. La Figura 4 muestra el por ciento de mejora del algoritmo G-FDCH-CS en términos de ETTR al incrementar en una unidad el número de radios. Se muestra además la relación:
la cual se traduce en el por ciento de incremento del costo energético por ranura en el G-FDCH-CS al aumentar en uno el número de radios. La Figura 4 permite observar cómo al aumentar el número de radios de un valor impar a uno par, se logra disminuir el tiempo de Rendezvous sin comprometer en gran medida el rendimiento energético. Por ejemplo, al aumentar el número de radios de dos a tres, el ETTR se reduce poco más del 45% con un incremento del costo energético de más del 80%, mientras cuando se aumenta k de 3 a 4 el ETTR vuelve a mejorar más de un 40% a costo de un incremento del factor energético inferior al 10%. Otro ejemplo que ilustra este comportamiento es al aumentar el número de radios de ocho a nueve con lo que se logra una mejora de ETTR en el algoritmo pero a un precio energético superior al 20%. Al aumentar el número de radios de nueve a diez, la mejora en términos de ETTR es casi la misma pero esta vez el aumento en el costo energético no sobrepasa el 5%.
Como se había observado de la Figura 3, con el aumento del número de radios se produce un aumento del costo energético por ranura de tiempo requerido para establecer el Rendezvous, el cual resulta perjudicial para el desempeño de los algoritmos. Sin embargo, también con el incremento del número de radios, disminuye el ETTR, lo que resulta beneficioso.

Figura 4 Por ciento de variación en la disminución del ETTR y el aumento del costo energético por ranura de tiempo ante el aumento del número de radios en el G-FDCH-CS.
Es evidente que al aumentar el número de radios por US en redes radio cognitivas, se establece una relación de compromiso entre el ETTR y el costo energético por ranura de tiempo. Tomando k∈ [2,10], la relación:
ETTR2/ETTRk (6)
representa en cuánto se logra disminuir el ETTR cuando son utilizados k radios con respecto a dos, mientras la relación:
representa en cuánto es necesario incrementar el costo energético por ranura de tiempo al utilizar k radios con respecto a dos. La Figura 5 muestra la relación:
lo que se refiere a cuánto se logró mejorar el ETTR, sobre cuánto fue necesario sacrificar el costo energético utilizando k radios con respecto a dos. La variable gamma (γ) podría traducirse además como ganancia o pérdidas en el rendimiento. El resultado de esta ecuación (8) permite identificar si con el aumento del número de radios, es mayor el beneficio en ETTR que el sacrificio en costo energético (γ>1, ganancia), viceversa (γ<1, pérdida), o si esta relación es lineal (γ=1).

Figura 5 Relación de compromiso que se establece entre el ETTR y el costo energético por ranura de tiempo ante el aumento del número de radios en los algoritmos RPS y G-FDCH-CS.
De la Figura 5 se observa que en el algoritmo RPS, la relación de compromiso entre estos dos factores se mantiene prácticamente constante y con valores muy cercanos a la unidad. Para este algoritmo, al aumentar el número de radios se logran tantos beneficios en el ETTR como son necesarios sacrificios en el costo energético. Aunque este resultado no es del todo perjudicial, tampoco es favorable. Si damos igual valor al ETTR y al factor energético, entonces el aumento del número de radios no es justificable.
Por otra parte, el algoritmo G-FDCH-CS ofrece valores de gamma superiores a la unidad a partir de cuatro radios. Estos valores aumentan con el incremento del número de radios, lo que se traduce en que para este algoritmo sí resulta justificable aumentar el número de radios debido a que los beneficios en tiempo superan cada vez más a los sacrificios energéticos. Todo esto permite reafirmar la superioridad del algoritmo G-FDCH-CS sobre el RPS en términos del comportamiento de la relación de compromiso que se establece entre el ETTR y el costo energético por ranura de tiempo.
5.2.2. RESULTADOS EN EL ESCENARIO NÚMERO 2
En este segundo escenario se considera que la potencia de recepción es mayor que la de transmisión. Se asume, según las especificaciones del CC2420 (ver Tabla 2), el valor de 57mW para la potencia de transmisión ( PtRTS y PtCTS ) y 63mW para la de recepción ( PtRTS y PtCTS ), mientras para el estado inactivo ( Pinact ) se asumen 60µW de consumo de potencia. La Figura 6 muestra los resultados de la simulación en términos de costo energético por ranura de tiempo para este escenario.
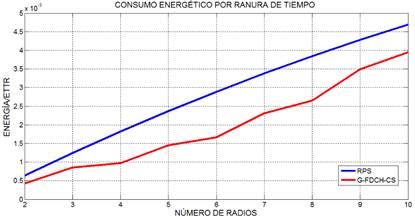
Figura 6 Resultados de la simulación del escenario número dos en términos de costo energético por ranura de tiempo.
En este escenario la potencia de transmisión es menor que en el escenario anterior mientras la potencia de recepción es mayor. Como se puede observar en la Figura 6, el comportamiento de los algoritmos es similar al observado en el escenario uno. Sin embargo, los valores para los costos energéticos por ranura de tiempo asociados a cada número total de radios desde dos hasta diez son inferiores aproximadamente en un 5% a los obtenidos en el escenario anterior para el algoritmo RPS. Esto coincide con la idea de que los radios receptores no influyen notablemente en el costo energético de los algoritmos, sobre todo en el RPS, donde solo se considera un único radio como receptor.
En el desempeño del G-FDCH-CS, se mantiene la forma escalonada, pero los valores disminuyen. Esto es debido a que al disminuir la potencia de transmisión, el costo energético por ranura de tiempo disminuye, incluso si se aumenta la potencia de recepción, producto de que los radios receptores permanecen la mayor parte del tiempo en estado inactivo. Incluso con estas variaciones en los valores de las potencias, el G-FDCH-CS sigue manteniendo mejor desempeño que el RPS, lo que se puede comprobar en la gráfica de gamma que se muestra en la Figura 7. En este escenario, gamma se comporta de manera similar que en el escenario anterior para ambos algoritmos. Sin embargo, para el G-FDCH-CS el comportamiento se acerca más a una forma escalonada como la descrita por el costo energético por ranura de tiempo al aumentar el número de radios.
5.2.3. RESULTADOS EN EL ESCENARIO NÚMERO 3
En este último escenario se considera que la potencia de transmisión es mayor que la de recepción. Se asume, según las especificaciones del CC1000 (ver Tabla 2), el valor de 75mW para la potencia de transmisión (PtRTS y PtCTS) y 36mW para la de recepción (PrRTS y PrCTS), mientras para el estado inactivo ( Pinact ) se asumen 100µW de consumo de potencia. La Figura 8 muestra los resultados de la simulación en términos de costo energético por ranura de tiempo para este escenario.

Figura 8 Resultados de la simulación del escenario número tres en términos de costo energético por ranura de tiempo.
En este escenario, la potencia de transmisión es mayor con respecto al escenario número uno, mientras la potencia de recepción es menor. Como se puede observar en la Figura 8, el comportamiento de los algoritmos es similar al observado en los escenarios anteriores. Sin embargo, los valores para los costos energéticos por ranura de tiempo asociados a cada número total de radios desde dos hasta diez son superiores aproximadamente en un 20% a los obtenidos en el escenario número uno para el algoritmo RPS.
Una vez más, esto coincide con la idea de que los radios receptores no influyen notablemente en el costo energético de los algoritmos. El desempeño del G-FDCH-CS, al igual que en el escenario dos, mantiene la forma escalonada, pero los valores aumentan. Esto es debido a que al aumentar la potencia de transmisión, el costo energético por ranura de tiempo aumenta, incluso si se disminuye la potencia de recepción, debido a que los radios receptores permanecen la mayor parte del tiempo en reposo.
En este escenario, gamma también se comporta de manera similar que en el escenario uno para ambos algoritmos. Sin embargo, para el G-FDCH-CS, como en el escenario 2, el comportamiento se acerca más a una forma escalonada como la descrita por el costo energético por ranura de tiempo al aumentar el número de radios, como se observa en la Figura 9.
6. CONCLUSIONES
Con el aumento del número de radios, el costo energético por ranura de tiempo asociado al funcionamiento simultáneo de los mismos durante el proceso de señalización aumenta tanto en el algoritmo RPS como en el G-FDCH-CS. En el RPS este aumento es lineal, mientras que en el G-FDCH-CS es similar a una escalera debido a la estrategia de asignación de roles a los radios cognitivos que se utilizan. Este último presenta mejor rendimiento que el RPS producto de que, a medida que aumenta el número total de radios, el valor del costo energético por ranura de tiempo para el G-FDCH-CS aumenta en menor medida con respecto al RPS. En ambos algoritmos el costo energético es similar para dos y tres radios, sin embargo, al llegar a diez radios, el costo energético del G-FDCH-CS representa el 75% del costo para el RPS.
En el algoritmo RPS, la relación de compromiso entre el comportamiento del ETTR y el costo energético se mantiene prácticamente constante con valores muy cercanos a la unidad. Para este algoritmo, al aumentar el número de radios, se logran tantos beneficios en el ETTR como son necesarios sacrificios en el costo energético. Por otra parte, el algoritmo G-FDCH-CS ofrece valores de gamma superiores a la unidad a partir de cuatro radios y estos valores aumentan con el incremento del número de radios. Para este algoritmo sí resulta justificable aumentar el número de radios puesto que los beneficios en tiempo superan cada vez más a los sacrificios energéticos, lo que constituye una ganancia en el rendimiento. Todo esto permite reafirmar la superioridad en rendimiento del algoritmo G-FDCH-CS sobre el RPS.