Artículo Original

Dependencia térmica de las propiedades eléctricas del tejido pulmonar a frecuencias entre 10 Hz y 100 kHz.

Thermal dependence of the electrical properties of lung tissue at frequencies between 10 Hz and 100 kHz.

0000-0003-0306-0941Roberto Vázquez Somoza^{1  *}  , 0000-0002-8216-9234Fidel Gilart González¹  , 0000-0002-0787-9201Ramón Gonzáles Couso² 

¹Universidad de Oriente, Centro Nacional de Electromagnetismo Aplicado, Santiago de Cuba, Cuba

²Hospital General “Juan Bruno Zayas”, Santiago de Cuba, Cuba

RESUMEN

Uno de los principales retos en el estudio de la interacción de los campos electromagnéticos con los tejidos biológicos es el conocimiento preciso de los parámetros eléctricos (permitividad y conductividad eléctrica) y térmicos (velocidad de transferencia de calor, conductividad térmica, velocidad de producción de calor y densidad de masa), los cuales determinan las formas en que los flujos de corriente y la deposición de calor tienen lugar y por lo tanto representan datos de entrada cruciales para el modelado y la simulación de los campos electromagnéticos y su efecto térmico en los tejidos. En este trabajo se presentan por primera vez los resultados de la caracterización de la dependencia térmica de las propiedades eléctricas del tejido pulmonar porcino durante el calentamiento de este in vitro desde 37 hasta 70 ºC a una velocidad de 5 ºC/min en el intervalo de frecuencias desde 10 Hz hasta 100 kHz. Para esto se construyó y validó una instalación experimental basada en un amplificador Lock-in, acoplada a una computadora, y se desarrollaron los programas de adquisición y procesamiento de los datos correspondientes. Se observó que hasta una temperatura de cerca de 50 ºC la conductividad del tejido aumenta linealmente con la temperatura para todas las frecuencias con una velocidad media de 1.810 %/ºC, mientras que la permitividad disminuye con una velocidad media de -0.563 %/ºC a las frecuencias por encima de 100 Hz y aumenta con una velocidad media de 6.100 %/ºC a las frecuencias por debajo de 1 kHz.

Palabras-clave: parámetros eléctricos; bioimpedancia eléctrica; calentamiento de tejidos biológicos; tejido pulmonar porcino

ABSTRACT

One of the main challenges in the study of the interaction of electromagnetic fields with biological tissues is the precise knowledge of the electric (permittivity and electrical conductivity) and thermal (rate of heat transfer, thermal conductivity, heat production rate, and mass density) parameters of these. They determine the ways in which current flows and heat depositions takes place and thus represent crucial input data for the modeling and simulation of electromagnetic fields and its thermal effect on tissues. In this work they are presented for the first time the results of the characterization of the thermal dependence of the electric parameters of the porcine lung tissue during its heating in vitro from 37 to 70 ºC with a heating rate of 5 ºC/min in the frequency range from 10 Hz to 100 kHz. For this, it was built and validated an experimental setup based on a Lock-in amplifier, coupled to a computer, and they were developed the corresponding data acquisition and processing software. It was observed that up to a temperature of about 50 ºC the conductivity of the tissue increases linearly with the temperature for all the frequencies with an average rate of 1.810 %/ºC, while the permittivity decreases with an average rate of -0.563 %/ºC, at frequencies above 100 Hz, and increases with an average rate of 6.100 %/ºC, at frequencies below 1 kHz.

Key words: electric parameters; electrical bioimpedance; biological tissue heating; porcine lung tissue

1. -INTRODUCCIÓN

El cáncer constituye la segunda causa de muerte en Cuba [¹] y el de mayor incidencia es el cáncer de pulmón, de ahí la importancia de conocer de forma precisa el comportamiento de las propiedades eléctricas del tejido de pulmón y como varían estas con la frecuencia y la temperatura en aras de desarrollar nuevas terapias y métodos de diagnósticos para el tratamiento de esta enfermedad.

A menudo, la espectroscopía dieléctrica de tejidos de animales y humanos es realizada ex vivo por razones de conveniencia o debido a dificultades para establecer protocolos de medición in vivo. En estos casos, las mediciones tienen lugar frecuentemente a la temperatura ambiente. Sin embargo, incluso durante los experimentos in vivo, la mayoría de las modalidades de medición requieren del contacto directo del sensor con el material bajo ensayo, y a menudo la temperatura de medición está por debajo de la normal del cuerpo. Además, ciertas tecnologías de tratamiento como la hipertermia y la ablación tienen lugar a temperaturas muy por encima de la normal del cuerpo humano (43 °C - 100 °C), por lo que se debe tener en cuenta el cambio correspondiente en las propiedades eléctricas del tejido.

Varios investigadores han medido las propiedades eléctricas de tejidos biológicos a frecuencias discretas y temperaturas variables hasta cerca de 43 °C y han presentado sus resultados en términos de coeficientes térmicos constantes definidos como cambios porcentuales por grados Celsius en la permitividad o la conductividad [²]. Aunque se puede esperar que tales coeficientes varíen con la frecuencia y la temperatura del tejido, los estudios anteriores sólo proporcionan valores para un número limitado de frecuencias discretas específicas y temperaturas. Además, la validez de los coeficientes térmicos constantes sobre amplios rangos de temperatura no ha sido investigada [³]. Se ha realizado también un gran número de investigaciones pertenecientes a la industria agropecuaria sobre la dependencia térmica de las propiedades eléctricas de las carnes [⁴,⁵], lo cual es relevante para predecir cómo la carne se descongelará, se calentará, y se cocinará en un horno de microondas. Estos estudios se han llevado a cabo a frecuencias discretas entre 915 y 2450 MHz, pero los coeficientes térmicos no han sido calculados.

Los coeficientes térmicos constantes de frecuencias discretas son imprácticos para las aplicaciones de ultra banda ancha ya que estos deben ser presentados para cada frecuencia y rango de temperaturas de interés, requiriendo la compilación de tablas de aspecto embarazoso, así como la interpolación de los datos a las frecuencias intermedias. Además, no está claro que tales coeficientes sean apropiados a todas las temperaturas y frecuencias [³].

Son escasos los estudios que han informado acerca de las propiedades eléctricas del tejido pulmonar. La mayoría de las investigaciones se han restringido a definiciones más bien cualitativas del denominado factor de llenado de aire, descritos, por ejemplo, como "inflación máxima" o "inspiración total" o "deflación máxima” [⁶], o al análisis del comportamiento de las propiedades eléctricas en tejido sano y tumoral [⁷], sin embargo hasta hoy no se ha encontrado ningún reporte sobre dependencias térmicas de las propiedades eléctricas del tejido pulmonar.

El conocimiento preciso de cómo cambian estas propiedades durante el calentamiento facilita la realización de simulaciones computacionales más confiables del desempeño de los dispositivos y ayuda a optimizar la geometría de estos y los parámetros de entrega de energía, reduciendo el número de estudios experimentales de validación requeridos.

Aunque esta investigación está enfocada al tejido de pulmón humano vivo, teniendo en cuenta lo complejo de establecer protocolos de medición in vivo tanto en tejidos humanos como de animales, en este trabajo se presentan resultados preliminares obtenidos sobre tejidos de pulmón de cerdo ex vivo, garantizando siempre que transcurra el menor tiempo posible entre el momento del sacrificio del animal y el inicio de las mediciones.

2.- Instalación experimental basada en un amplificador Lock-in.

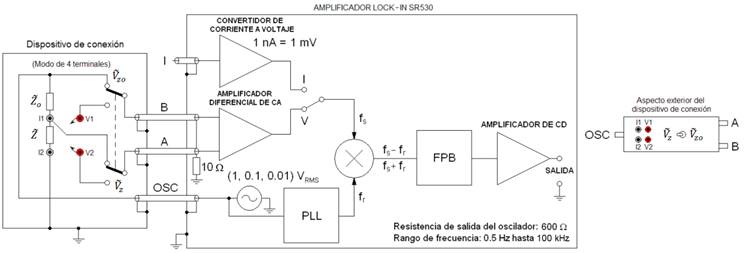
La Figura 1 muestra el esquema en bloques de la instalación experimental desarrollada en este trabajo para la determinación de propiedades eléctricas de tejidos biológicos y su dependencia con la temperatura, basada en un amplificador Lock-in. Se desarrolló el software control_sr530 para el control de las funciones del equipo desde la PC y el software z_procesa para el cálculo de la conductividad y permitividad a partir de los valores de impedancia medidos con el amplificador Lock-in.

El amplificador Lock-in no es un instrumento de medición diseñado específicamente con el propósito de realizar mediciones de bioimpedancia. Sin embargo, teniendo en cuenta las características de este dispositivo, tales como la posibilidad de generar corrientes de muy baja intensidad con una alta estabilidad, la alta resistencia de entrada del amplificador diferencial de CA y el rango de frecuencias de trabajo, entre otras, se infirió la posibilidad de implementar con este un medidor de impedancia acoplándole un dispositivo de conexión (conmutador) con el objetivo de implementar el método de medición de dos lecturas [⁸], cuyo esquema general de funcionamiento se muestra en la Figura 2.

Figura 1 Esquema en bloques de la instalación experimental desarrollada basada en un amplificador Lock-in. Se construyeron los electrodos de medición, el portamuestras con los electrodos de calentamiento por RF y el dispositivo de conmutación. 

Figura 2 Esquema del analizador de impedancia basado en un amplificador Lock-in. 

Las entradas A y B son entradas de tensión con una impedancia de entrada de 100 MΩ, 25 pF. La entrada I es una entrada de corriente con una impedancia de entrada de 1 kΩ a una tierra virtual. En la Figura 2 el dispositivo de conexión se muestra en el modo de 4 terminales. El modo de dos terminales se configura uniendo los bornes V1 con I1 y V2 con I2.

El analizador de impedancia implementado utiliza el oscilador interno del amplificador Lock-in como fuente de excitación de corriente a través de la muestra para la medición de la impedancia de esta. La señal de excitación del oscilador se puede variar en el rango de 0.01-1V.

Se utiliza la entrada de tensión diferencial (A-B) del Lock-in acoplada al dispositivo de conexión, el cual tiene un interruptor para la conmutación de medición de los fasores ${\tilde{V}}_{zo}$ y ${\tilde{V}}_z$ , cuyas amplitudes son del orden de los mV.

2.1.- Método de medición de impedancia utilizando un amplificador Lock-in SR530

La determinación de la impedancia $\tilde{Z}$ mediante el método de medición de dos lecturas se basa en los siguientes cálculos:

$\tilde{Z}=\frac{{\tilde{V}}_z}{\tilde{I}} =\frac{{\tilde{V}}_z}{{\tilde{V}}_{zo}}{\tilde{Z}}_o=\frac{V_z{e}^{j{\theta }_{vz}}}{V_{z_0}{e}^{j{\theta }_{v{z}_0}}}{Z}_0{e}^{j{\theta }_{z_0}}$ (1)

o bien

$\tilde{Z}=\frac{V_z}{V_{z_0}}{Z}_0{e}^{j\left({\theta }_{vz}+{\theta }_{z_0}-{\theta }_{v{z}_0}\right)}=Z{e}^{j\left({\theta }_{vz}+{\theta }_{z_0}-{\theta }_{v{z}_0}\right)}=Z{e}^{j{\theta }_z}$ (2)

El ángulo ${\theta }_{zo}$ se calcula a partir de ${\tilde{Z}}_o$ utilizando:

${\tilde{Z}}_o=R_{cao}+j{X}_o$ (3)

donde

$R_{cao}=\frac{R_o}{R_o^2{\omega }^2{C}^2+{\left(\frac{{\omega }^2}{{\omega }_o^2}-1\right)}^2}$ (4)

${\begin{array}{c} \\ X\end{array}}_o=-\frac{\omega \left[R_o^{2}C+L\left(\frac{{\omega }^2}{{\omega }_o^2}-1\right)\right]}{R_o^2{\omega }^2{C}^2+{\left(\frac{{\omega }^2}{{\omega }_o^2}-1\right)}^2}$. (5)

${\omega }_o=\frac{1}{\sqrt{LC}}$ (6)

$Z_o=\sqrt{R_{cao}^2+X_o^2}$ (7)

${\theta }_{zo}={\tan }^{-1}\left(X_o/R_{cao}\right)$ (8)

${\omega }_o$ es la frecuencia de resonancia del resistor patrón,

$R_o$ es la resistencia de CD, L es la inductancia residual y C es la capacidad en paralelo del resistor patrón. Los valores de $R_o$ , L y C fueron determinados utilizando un método y un software desarrollados anteriormente en el Laboratorio de Caracterizaciones Magnéticas del CNEA (en trámites de registro).

Se obtuvieron los siguientes valores: $R_o$ = 470 $\text{Ω}$ , L = 5.063 µH, C = 70 pF.

De esta forma, calculados $Z_0$ y ${\theta }_{z_0}$ , datos que se introducen como parámetros fijos al software z_procesa, y midiendo $V_z$ , ${\theta }_{vz}$ , $V_{zo}$ , ${\theta }_{vzo}$ , los que se le cargan al software z_procesa a través del software control_sr530 desarrollado como parte de este trabajo para la interface entre el equipo Lock-in y la computadora, se obtienen $Z$ y ${\theta }_z$ a partir de (2).

2.2.- Relación entre impedancia, conductividad y permitividad

A similitud con la ley de Ohm y Pouillet, $R=l/\left(\sigma S\right)$ , la impedancia $\tilde{Z}$ se puede expresar en la forma

$\tilde{Z}=R_{ca}+jX=\frac{k}{\tilde{\sigma }}=\frac{k}{\sigma +j\omega \epsilon }$ (9)

donde $\tilde{\sigma }$ es la conductividad compleja, $\sigma$ y $\epsilon$ son la conductividad y la permitividad absoluta del medio, respectivamente, y k es un factor de forma. Por tanto

$\tilde{Z}=\frac{\sigma -j\omega \epsilon }{{\sigma }^2+{\left(\omega \epsilon \right)}^2}k=\frac{\sigma }{{\sigma }^2+{\left(\omega \epsilon \right)}^2}k-j\frac{\omega \epsilon }{{\sigma }^2+{\left(\omega \epsilon \right)}^2}k$ (10)

Comparando (9 y 10)

$R_{ca}=\frac{\sigma }{{\sigma }^2+{\left(\omega \epsilon \right)}^2}k$ (11)

$X=-\frac{\omega \epsilon }{{\sigma }^2+{\left(\omega \epsilon \right)}^2}k$ (12)

De (11) y (12)

$\omega \epsilon =-\frac{\sigma X}{R_{ca}}$ (13)

Sustituyendo (13) en (11) se obtiene

$\sigma =\frac{R_{ca}k}{R_{ca}^2+X^2}$ (14)

Sustituyendo (13) en el denominador de (12) se obtiene

$\epsilon =-\frac{X\left(R_{ca}^2+X^2\right){\sigma }^2}{\omega R_{ca}^{2}k}$ (15)

Las expresiones (14) y (15) permiten calcular la conductividad y la permitividad absoluta del medio, respectivamente, a partir del conocimiento del factor de forma y de la parte real y la parte imaginaria de la impedancia a la frecuencia dada.

2.3.- Relación de C _p y G _ca con el factor de forma en un circuito RC paralelo

Generalizando la expresión de la resistencia de un resistor homogéneo de sección transversal de conducción constante a la de uno con sección transversal variable:

$R_p=\frac{k}{\sigma }$ (16)

Por tanto

$G_{ca}\equiv \frac{1}{ R_p}=\frac{\sigma }{k}$ (17)

Por otro lado, generalizando la expresión de la capacidad de un capacitor plano paralelo a la de uno de sección transversal de conducción variable, lleno de un dieléctrico homogéneo

$C_p=\frac{{\epsilon }_0{\epsilon }_r}{k}$ (18)

Definiendo un nuevo factor de forma como

$K\equiv \frac{1}{k}$ (19)

Se puede escribir

$G_{ca}=K\sigma$ (20)

$C_p=K{\epsilon }_0{\epsilon }_r$ (21)

El factor de forma $K$ es preferido por algunos autores. En este trabajo el factor de forma considerado es el $k$ . Conociendo $k,G_{ca}$ y $C_p$ , la conductividad y la permitividad relativa se pueden determinar utilizando

$\sigma =k{G}_{ca}$ (22)

${\epsilon }_r=\frac{k{C}_p}{{\epsilon }_0}$ (23)

$G_{ca}$ y $C_p$ se determinan a partir de la parte real y la parte imaginaria de la admitancia $\tilde{Y}$ medida:

$\tilde{Y}=\frac{1}{\tilde{Z}}=G_{ca}+j\omega C_p$ (24)

2.4.- Electrodos de medición

Se construyó un arreglo lineal de 4 electrodos de medición utilizando agujas hipodérmicas de acero inoxidable número 26 (0,46 mm), (Figura 3). Los electrodos están separados entre sí a una distancia de 2.3 mm y tienen una longitud de 5 mm. Los dos electrodos de los extremos se utilizaron para inyectar corriente a través de la muestra y los dos electrodos interiores para realizar la lectura o medición del fasor de tensión.

Figura 3 Arreglo de 4 electrodos de medición construido.  

2.5.- Portamuestras

Se construyó un portamuestras en forma de tubo cilíndrico utilizando un material aislante térmico (polietileno) a través de cuyos extremos se insertaron dos electrodos de acero inoxidable de 35 mm de diámetro para acoplarlos al equipo electrocoagulador de RF, con el objetivo de calentar el tejido como se muestra en la Figura 1. Todo el conjunto anterior, incluyendo el arreglo de electrodos para la medición de impedancia, se acomodó en el interior de una caja de espuma de poliestireno para garantizar que fuera lo más adiabático posible.

2.6.- Determinación del factor de forma

Para determinar el factor de forma $k=\sigma /G_{ca}$ se procedió mediante un método experimental desarrollado en [⁹] que consiste en medir la conductancia de cinco soluciones de cloruro de sodio (NaCl) a diferentes concentraciones $c_{NaCl}$ que varían de 0.001 M a 0.15 M (este rango cubre los valores de conductividad para la mayoría de los tejidos biológicos) y a las frecuencias de trabajo. Las mediciones se realizaron a 24 ºC y los resultados obtenidos para la conductancia se muestran en la Figura 4.

Figura 4 Conductancia de las soluciones de NaCl a diferentes concentraciones.  

Para cada concentración se calcularon los valores promedios de la conductancia correspondientes a las cinco frecuencias de trabajo. Con los resultados obtenidos se calcularon cinco valores del factor de forma, correspondientes a las concentraciones consideradas utilizando la ecuación (23) con los valores de conductividad correspondientes a cada concentración según Peyman y col. [¹⁰].

Teóricamente, las soluciones iónicas como el NaCl acuoso no muestran dispersión dieléctrica a frecuencias inferiores a 1 MHz, sin embargo, en la práctica, la polarización de los electrodos y otros artefactos experimentales introducen variaciones dependientes de la frecuencia, por lo que resulta recomendable este método de ajuste.

En la Tabla 1 se muestran los resultados de los valores obtenidos para los promedios de la conductancia, los valores correspondientes del factor de forma, el valor medio del factor de forma y su desviación estándar. Los valores de la conductividad utilizados para calcular los factores de forma k aparecen en la segunda columna y fueron tomados de Peyman y col. [¹⁰].

Tabla 1 Conductancias promedio para cada concentración y factor de forma obtenido 

$c_{NaCl}$ (M)	$\sigma \left(S/m\right)$ Peyman y col. (95)	$G_{ca}\left(S\right)$ promedio	k (m^-1)	$\overline{k} \left(m^{-1}\right)$	$k_{std} \left(m^{-1}\right)$
0.001	1.01 x 10^-2	3.70 x 10^-4	27.30	27.11	1.66
0.005	5.05 x 10^-2	2.00 x 10^-3	25.25
0.01	1.01 x 10^-1	3.95 x 10^-3	25.57
0.05	5.01 x 10^-1	1.75 x 10^-2	28.63
0.15	1.48	5.14 x 10^-2	28.79

2.7.- Equipo de RF

En el trabajo se utilizó un electrocoagulador de RF de la marca SKYLUS, Super Frecator 2000, comercializado por la compañía Yamada Shadowless Lamp Co. LTD de Tokyo, Japón (Figura 5). Este es un equipo electrónico capaz de transformar la energía eléctrica de RF en calor con el fin de coagular tejido blando, eligiendo para esto corrientes que se desarrollan en frecuencias por encima de los 200 kHz, ya que éstas no interfieren con los procesos nerviosos y sólo producen calor.

Figura 5 Electrocoagulador SKYLUS. 

2.8.- Termómetro digital

Como termómetro para medir la temperatura en el tejido biológico se utilizó un multímetro digital inteligente de la marca UNI-T, modelo UT71A (Figura 6), provisto de un termopar del tipo K NiCr-NiSi con calibración interna, el cual permite medir temperaturas entre -40 °C y 1000 °C con una resolución de 0.1 °C y una precisión de ± 1 % de la lectura.

Figura 6 Multímetro digital utilizado como termómetro. 

3.- Modelos basados en una función de Arrhenius

Los procesos de daños térmicos en células y tejidos se cuantifican generalmente mediante modelos cinéticos basados ​​en un proceso de tasa de primer orden. La formulación de Arrhenius se utiliza comúnmente para describir la tasa de reacciones químicas que involucran la temperatura [¹¹-¹³]. A pesar de algunas limitaciones, este método se ha utilizado con éxito durante varias décadas para predecir y analizar múltiples alteraciones térmicas irreversibles en proteínas estructurales.

El índice de daño celular $u\left(t\right)$ se define como:

$u\left(t\right)=\text{ln}\left[\frac{c\left(0\right)}{c\left(t\right)}\right]$ (25)

donde $c\left(0\right)$ es la concentración inicial de células no dañadas antes del calentamiento y $c\left(t\right)$ es la concentración de células no dañadas después del calentamiento. El modelo de Arrhenius asume la siguiente relación entre la tasa de acumulación de daño térmico $k$ y la temperatura absoluta $T_k$

$k\left(t\right)=A{e}^{-\frac{E_a}{R{T}_k\left(t\right) }}$ (26)

donde $A$ es el factor de frecuencia ( ${\text{s}}^{-1}$ ), $E_a$ es la energía de activación ( ${\text{J mol}}^{-1}$ ) y $R$ es la constante universal de los gases (8.314 ${\text{J mol}}^{-1}{\text{K}}^{-1}$ ). El índice de daño térmico se calcula como:

$u\left(t\right)={{\displaystyle \int }}_0^{t}A{e}^{-\frac{E_a}{R{T}_k\left(\tau \right) }}d\tau$ (27)

Al igual que en [¹³], en este trabajo las dependencias de las propiedades eléctricas del tejido pulmonar con la temperatura fueron modeladas utilizando un tramo inicial lineal (efecto reversible) seguido de un tramo no lineal (efecto irreversible relacionado con cambios estructurales).Ya que la máxima temperatura alcanzada por el tejido (70 ºC) estuvo muy por debajo de los 100 ºC, el tramo no lineal fue modelado utilizando solamente la formulación de Arrhenius. De esta forma, los cambios en la conductividad eléctrica se modelaron utilizando la siguiente ecuación:

$\sigma ={\sigma }_{37}\left[1+{\alpha }_{\sigma }\left(T-37\right)+{\beta }_{\sigma }(1-\text{exp}\left(-u_{\sigma }\right)\right]$ (28)

donde ${\sigma }_{37}$ es la conductividad del tejido a 37 °C, ${\alpha }_{\sigma }$ es el coeficiente térmico de conductividad correspondiente a la referencia de 37 ºC, ${\beta }_{\sigma }$ es el coeficiente de daño térmico relacionado con la rotura de membranas y $u_{\sigma }$ es el índice de daño térmico referido a la conductividad dado por:

$u_{\sigma }\left(t\right)={{\displaystyle \int }}_0^t{A}_{\sigma }{e}^{-\frac{E_{a\sigma }}{R{T}_k\left(\tau \right) }}d\tau$ (29)

Para la permitividad se utilizó:

$\epsilon ={\epsilon }_{37}\left[1+{\alpha }_{\epsilon }\left(T-37\right)+{\beta }_{\epsilon }(1-\text{exp}\left(-u_{\epsilon }\right)\right]$ (30)

donde ${\epsilon }_{37}$ es la permitividad del tejido a 37 °C, ${\alpha }_{\epsilon }$ es el coeficiente térmico de permitividad correspondiente a 37 ºC, ${\beta }_{\epsilon }$ es el coeficiente de daño térmico relacionado con la rotura de membranas y $u_{\epsilon }$ es el índice de daño térmico referido a la permitividad dado por:

$u_{\epsilon }\left(t\right)={{\displaystyle \int }}_0^t{A}_{\epsilon }{e}^{-\frac{E_{a\epsilon }}{R{T}_k\left(\tau \right) }}d\tau$ (31)

Del análisis de la ecuación (28) se infiere que la pendiente (la velocidad de variación con la temperatura) del tramo lineal viene dada por $m_{\sigma }={\sigma }_{37}{\alpha }_{\sigma }$ . Por su parte, la pendiente de la curva normalizada a ${\sigma }_{37}$ es $m_{\sigma n}={\alpha }_{\sigma }$ . Usualmente la pendiente del tramo lineal de la dependencia de la conductividad con la temperatura se expresa en $\text{\%}/℃$ . En este caso la pendiente se puede calcular utilizando $p_{\sigma }=m_{\sigma n}\times 100={\alpha }_{\sigma }\times 100$ . Correspondientemente, en el caso de la ecuación (30) para la permitividad se obtienen $m_{\epsilon }={\sigma }_{37}{\alpha }_{\epsilon }$ , $m_{\epsilon n}={\alpha }_{\epsilon }$ y $p_{\epsilon }=m_{\epsilon n}\times 100={\alpha }_{\epsilon }\times 100$ .

4.- Resultados y discusión

4.1.- Espectroscopía dieléctrica del tejido pulmonar porcino a 37 °C

Se hicieron mediciones de impedancia eléctrica a 9 muestras de tejido pulmonar porcino a la temperatura de 37 °C y frecuencias de 10 Hz, 100 Hz, 1000 Hz, 10 kHz y 100 kHz determinando la conductividad y la permitividad relativa de estas. Las muestras de tejido se obtuvieron de diferentes lóbulos del pulmón de cerdo y, teniendo en cuenta los cambios post mórtem que se producen en estas, todas fueron medidas con no más de 1 hora de haber sido sacrificado el animal [¹⁴].

A los datos obtenidos se les determinaron el valor medio y la desviación estándar. En la Figura 7 se muestran los resultados junto con los reportados por otros autores [¹⁵,¹⁶] para las mediciones in vitro del tejido pulmonar inflado. Los datos de la literatura se encuentran dispersos en el espacio comprendido entre las dos curvas con trazo discontinuo correspondientes a la propiedad dada. Las curvas con trazo continuo representan los ajustes de los datos de la literatura a un modelo paramétrico de Cole-Cole con cuatro regiones de dispersión realizado por Gabriel y col. [¹⁵].

Como se puede ver, los valores obtenidos muestran una buena correspondencia con los resultados reportados en la literatura. La gran dispersión de los valores reportados en la literatura que se observa en el intervalo de frecuencias considerado se debe a que a frecuencias por debajo de 1 MHz las propiedades eléctricas dependen fuertemente del estado fisiológico, el grado de perfusión, el peso, la edad, así como el tiempo transcurrido después de la muerte. Otros factores que influyen son: (a)- la polarización de los electrodos, la cual es una fuente de errores sistemáticos importante a frecuencias por debajo de 100 Hz, aun cuando se tomen precauciones para minimizar su efecto, (b)- el contenido de aire del tejido pulmonar, (c)- la heterogeneidad de la muestra. Es probable que el comportamiento de la permitividad para los resultados obtenidos en este trabajo con pendiente diferente a la de la curva ajustada por Gabriel y col. [¹⁵] se deba al pequeño tamaño de la muestra.

En otro trabajo Gabriel y col. [⁹] reportaron los resultados de las mediciones in vivo de la conductividad eléctrica del tejido pulmonar en estado inflado y desinflado a la temperatura de 37 ºC en el intervalo de frecuencias entre 10 Hz y 1 MHz, realizadas por ellos. En la Figura 8 se muestran superpuestos tales resultados y los correspondientes obtenidos en este trabajo. Como se puede ver estos ( ${\sigma }_{10\text{Hz}}=0.0324\pm 0.0138 \text{S}/\text{m}$ , ${\sigma }_{100\text{Hz}}=0.0407\pm 0.0099 \text{S}/\text{m}$ , ${\sigma }_{1\text{kHz}}=0.0444\pm 0.0105 \text{S}/\text{m}$ , ${\sigma }_{10\text{kHz}}=0.0494\pm 0.0132 \text{S}/\text{m}$ , ${\sigma }_{100\text{kHz}}=0.0705\pm 0.0241 \text{S}/\text{m}$ ) muestran una buena correspondencia con los obtenidos por Gabriel y col. [⁹] para el tejido pulmonar en estado inflado. Esto permite inferir que aunque el contenido de aire de las muestras de tejido pulmonar estudiadas no fue controlado, el estado predominante de las mismas fue el inflado. Por otro lado, comparando los resultados mostrados en las Figuras 7 y 8 con los valores de la conductividad eléctrica contenidos en la base de datos [¹⁶] para el tejido pulmonar inflado de cadáveres humanos frescos ( ${\sigma }_{10\text{Hz}}=0.060 \text{S}/\text{m}$ , ${\sigma }_{100\text{Hz}}=0.075 \text{S}/\text{m}$ , ${\sigma }_{1\text{kHz}}=0.080 \text{S}/\text{m}$ , ${\sigma }_{10\text{kHz}}=0.095 \text{S}/\text{m}$ , ${\sigma }_{100\text{kHz}}=0.105 \text{S}/\text{m}$ ), se puede notar que estos últimos, aunque son ligeramente superiores a los obtenidos de las mediciones in vitro aquí e in vivo en Gabriel y col. [⁹] a 37 ºC, se encuentran entre las dos curvas con trazo discontinuo correspondientes a la conductividad en la Figura 7.

Figura 7 Comparación de los resultados obtenidos en este trabajo con los reportados en la literatura para el tejido pulmonar inflado y el ajuste paramétrico de estos a un modelo paramétrico de Cole-Cole de dispersión múltiple realizado por Gabriel y col. [¹⁵]. Los círculos representan el valor medio y las barras verticales la desviación estándar de las mediciones de 9 cerdos diferentes.  

4.2.- Dependencias térmicas de las propiedades eléctricas del tejido pulmonar porcino

Se hicieron mediciones de 9 muestras de tejido pulmonar porcino, a todas las frecuencias consideradas, en el intervalo de temperaturas desde 37 ºC hasta 70 ºC, con una velocidad media de calentamiento de 5 ºC/min, a las que se le determinó el valor medio y la desviación estándar de la conductividad y la permitividad a cada temperatura. Haciendo uso del software z_procesa desarrollado en este trabajo, los valores medios anteriores fueron suavizados mediante un filtro de media móvil, y luego ajustados a las funciones descritas por las ecuaciones (28) y (30). La media móvil es uno de los filtros más comunes en el procesamiento digital de señales, siendo óptimo para el suavizado de datos en el dominio del tiempo. Se seleccionó el menor tamaño posible de la ventana ( $n=2$ ) con el objetivo de afectar lo menos posible el comportamiento de los datos a larga escala.

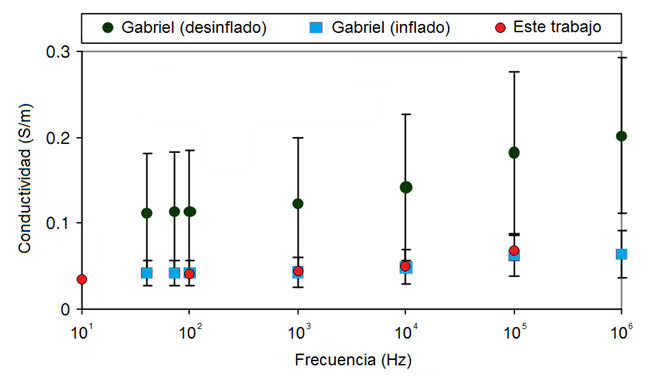
Figura 8 Espectro del tejido pulmonar de cerdo en los estados inflado y desinflado: comparación de las mediciones in vivo de Gabriel [⁹] a 37 ºC con las mediciones in vitro realizadas en este trabajo a la misma temperatura. Las barras verticales representan la desviación estándar de las mediciones de 6 cerdos diferentes. 

En las Tablas 2 y 3 siguientes se resumen los resultados numéricos de los ajustes.

Tabla 2 Resultados del ajuste de la conductividad 

Frecuencia:	Mejor coeficiente térmico de conductividad: ${\alpha }_{\sigma }\left({℃}^{-1}\right)$	Mejor coeficiente de daño térmico: ${\beta }_{\sigma }$	Mejor energía de activación de Arrhenius: $E_{a\sigma }\left(J/mol\right)$	Mejor factor de frecuencia de Arrhenius: $A_{\sigma }\left(s^{-1}\right)$	Mínimo error cuadrático medio: ${\delta }_{min}\left(\%\right)$
10 Hz	0.0270	0.65	2.880 x 10^5	3.700 x 10^43	2.4962
100 Hz	0.0190	0.80	2.920 x 10^5	1.714 x 10^44	3.1708
1 kHz	0.0190	0.57	2.920 x 10^5	1.714 x 10^44	2.4602
10 kHz	0.0145	0.59	2.920 x 10^5	1.714 x 10^44	2.4598
100 kHz	0.0110	0.27	2.920 x 10^5	1.714 x 10^44	1.5911

Tabla 3 Resultados del ajuste de la permitividad 

Frecuencia:	Mejor coeficiente térmico de conductividad: ${\alpha }_{\epsilon }\left({℃}^{-1}\right)$	Mejor coeficiente de daño térmico: ${\beta }_{\epsilon }$	Mejor energía de activación de Arrhenius: $E_{a\epsilon }\left(J/mol\right)$	Mejor factor de frecuencia de Arrhenius: $A_{\epsilon }\left(s^{-1}\right)$	Mínimo error cuadrático medio: ${\delta }_{min}\left(\%\right)$
10 Hz	0.0510	-0.97	2.240 x 10^5	8.265 x 10^32	2.3527
100 Hz	0.0710	-0.20	2.920 x 10^5	1.714 x 10^44	2.8117
1 kHz	-0.0050	0.40	2.300 x 10^5	8.237 x 10^33	0.9771
10 kHz	-0.0039	-0.15	3.150 x 10^5	1.152 x 10^48	1.1882
100 kHz	-0.0080	-0.13	2.920 x 10^5	1.714 x 10^44	1.3382

Como se puede ver, el mínimo error cuadrático medio obtenido fue inferior a un 4 % en todos los casos, por lo que los ajustes realizados a los datos se pueden considerar buenos.

En las Figuras 9 y 10 se muestran las dependencias térmicas obtenidas (datos y curvas de interpolación lineal de los datos suavizados) a todas las frecuencias para la conductividad eléctrica y la permitividad relativa del tejido pulmonar porcino, respectivamente.

Como ocurre con otros tejidos biológicos [¹³, ¹⁷], la conductividad del tejido pulmonar porcino medido en este trabajo experimenta un aumento con el aumento de la temperatura cuyos valores en el rango de frecuencias estudiado, de 10 Hz a 100 kHz y temperaturas entre 37 °C y 70 °C se encuentran entre 0.0474 ± 0.0142 S/m y 0.0990 ± 0.0120 S/m. Al igual que en los resultados mostrados en la Figura 11, obtenidos para el tejido hepático porcino por Deás y col. [¹⁷] a una velocidad de calentamiento de 3 ºC/min, en los resultados de la conductividad eléctrica obtenidos en este trabajo para el tejido pulmonar porcino a una velocidad de calentamiento de 5 ºC/min se observa una disminución de la pendiente del tramo recto de la función $\sigma \left(T\right)$ con el aumento de la frecuencia ( ${\sigma }_{37}{\alpha }_{\sigma }$ disminuye desde un valor de 0.00086 S/m/ºC a 10 Hz hasta un valor de 0.00077 S/m/ºC a 100 kHz, o lo que es equivalente, la pendiente del tramo recto de la función $\sigma \left(T\right),$ expresada en %/ºC, $p_{\sigma }={\alpha }_{\sigma }\times 100$ , disminuye desde un valor de 2.7 %/ºC a 10 Hz hasta un valor de 1.1 %/ºC a 100 kHz ).

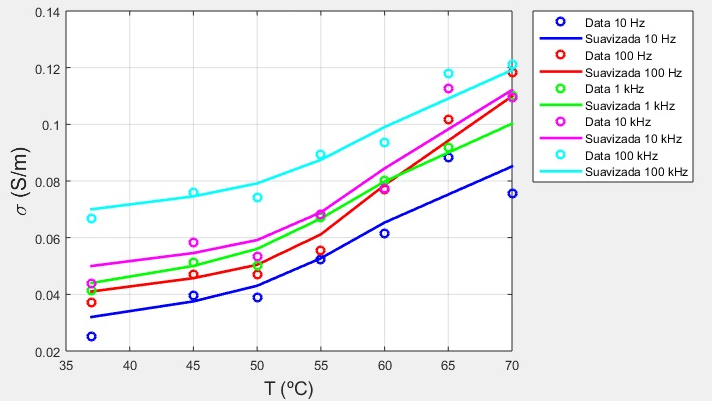
Figura 9 Dependencias térmicas obtenidas (datos y curvas de interpolación lineal de los datos suavizados) a todas las frecuencias para la conductividad eléctrica del tejido pulmonar porcino. 

Con relación a la permitividad, para frecuencias por debajo de 1 kHz los resultados muestran un aumento inicial de esta propiedad con la temperatura seguido de una disminución (notable principalmente a la frecuencia de 10 Hz en la Figura 10), mientras que a frecuencias por encima de 1 kHz se observa una disminución de la permitividad con el aumento de la temperatura. Estos resultados están en concordancia con lo reportado por otros investigadores para otros tejidos biológicos [¹³, ¹⁷]. En el caso de los resultados obtenidos por Deás y col. [¹⁷] para el tejido hepático porcino durante el calentamiento de este desde 37 hasta 100 ºC a frecuencias entre 5 kHz y 500 kHz, a una velocidad de calentamiento de 3 ºC/min (ver Figura 12) la frecuencia de transición entre los dos comportamientos mencionados anteriormente es de 50 kHz.

Figura 10 Dependencias térmicas obtenidas (datos y curvas de interpolación lineal de los datos suavizados) a todas las frecuencias para permitividad relativa del tejido pulmonar porcino. 

Figura 11 Dependencias térmicas de la conductividad del tejido hepático porcino obtenidas por Deás y col. [¹⁷] para frecuencias entre 5 kHz y 500 kHz a una velocidad de calentamiento de 3 ºC/min. 

Como se observa, todas las curvas obtenidas para las dependencias térmicas de la conductividad y la permitividad del tejido pulmonar porcino presentan un tramo inicial lineal, el cual se mantiene hasta una temperatura de alrededor de 50 ºC, lo que está en concordancia con lo reportado para otros tejidos biológicos. Se debe destacar que la extensión de este tramo lineal es dependiente de la velocidad de calentamiento, según ha sido reportado por Macchi y col. [¹³] y Deás y col. [¹⁷,¹⁸]. Esos autores han atribuido la pérdida de la linealidad de las mencionadas dependencias térmicas a la aparición de daños estructurales irreversibles en los tejidos biológicos, conectados con la ruptura de las membranas celulares e intracelulares, lo que conduce al escape de los contenidos celulares (agua, iones, micromoléculas y macromoléculas) hacia el espacio extracelular. Este fenómeno ha sido denominado desestructuración del tejido por Macchi y col. [¹³]. Del análisis de las ecuaciones (28) y (30) se evidencia que la pendiente ( ${\alpha }_{\sigma }$ o ${\alpha }_{\epsilon }$ según sea el caso) del tramo inicial lineal de las curvas de conductividad y permitividad normalizadas al valor de referencia correspondiente es independiente de este valor.

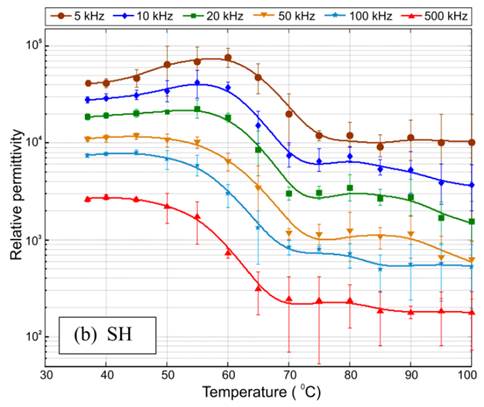
Figura 12 Dependencias térmicas de la permitividad relativa del tejido hepático porcino obtenidas por Deás y col. [¹⁷] para frecuencias entre 5 kHz y 500 kHz a una velocidad de calentamiento de 3 ºC/min. 

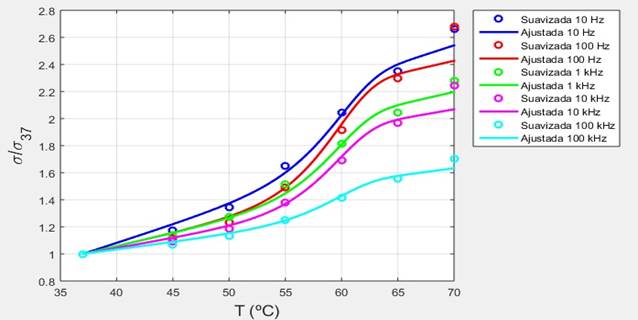
Figura 13 Dependencias térmicas de la conductividad eléctrica del tejido pulmonar porcino (suavizada y ajustada) normalizadas al valor de referencia de 37 ºC. 

A las frecuencias consideradas en este trabajo los valores de referencia de la conductividad y la permitividad correspondientes a una misma temperatura, en un mismo tejido biológico, son afectados por varios factores, tales como el peso, la edad, la heterogeneidad de la muestra, así como el tiempo transcurrido después de la muerte, razón por la cual varios investigadores [¹³, ¹⁷] han preferido reportar en sus trabajos los valores de la conductividad y la permitividad normalizados al valor de referencia correspondiente. En las Figuras 13 y 14 se muestran las dependencias térmicas obtenidas en este trabajo para la conductividad eléctrica y la permitividad, normalizadas al valor de referencia correspondiente de 37 ºC.

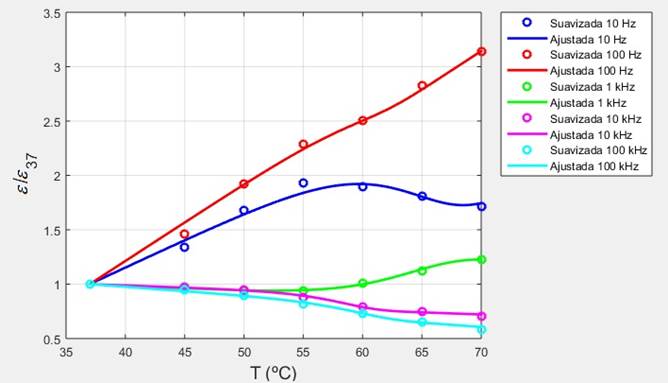
Figura 14 Dependencias térmicas de la permitividad del tejido pulmonar porcino (suavizada y ajustada) normalizadas al valor de referencia de 37 ºC. 

Usualmente los investigadores han reportado las variaciones lineales de la conductividad eléctrica y la permitividad de los tejidos biológicos con la temperatura en términos de la pendiente de la recta (velocidad de variación con la temperatura) expresada en %/ºC. Los datos reportados [³, ¹⁹] evidencian que para todos los tejidos biológicos a todas las frecuencias hasta cerca de 1 GHz, la conductividad aumenta con la temperatura con una velocidad media de alrededor de 2 %/ºC.

En el caso de la permitividad a las mismas frecuencias anteriores, se observa que esta aumenta o disminuye con la temperatura según el sub intervalo de frecuencias considerado. Presman [¹⁹] ha reportado para la permitividad de todos los tejidos biológicos en los intervalos de frecuencia en que esta disminuye con la temperatura una velocidad media de disminución de cerca de -0.5 %/ºC. A manera de comparación, en la región lineal de la curva de $\sigma \left(T\right)$ en este trabajo se obtuvo una velocidad media de aumento de la conductividad con la temperatura de 1.810 %/°C a todas las frecuencias, mientras que para la permitividad se obtuvo una velocidad de disminución media de -0.563 %/ºC a las frecuencias por encima de 100 Hz. A las frecuencias por debajo de 1 kHz se obtuvo una velocidad media de aumento de la permitividad con la temperatura de 6.100 %/ºC.

5.- CONCLUSIONES

Se diseñó y se construyó una instalación experimental automatizada para la determinación de los parámetros eléctricos de tejidos biológicos y su dependencia con la temperatura basada en un amplificador Lock-in. Los resultados obtenidos para la dependencia de la conductividad y la permitividad del tejido pulmonar porcino con la frecuencia en el intervalo entre 10 Hz y 100 kHz a la temperatura de 37 ºC mostraron una buena correspondencia con los resultados reportados en la literatura, lo que permitió validar la instalación experimental construida. Los datos obtenidos de las dependencias térmicas de la conductividad y la permitividad del tejido pulmonar porcino fueron suavizados y después ajustados a una función no lineal de la temperatura, la cual incluye un tramo inicial lineal y un tramo final curvo descrito por una función de daño térmico de Arrhenius. Se observó que hasta una temperatura de cerca de 50 ºC la conductividad aumenta linealmente con la temperatura para todas las frecuencias con una velocidad media de 1.810 %/ºC, mientras que la permitividad disminuye con una velocidad media de -0.563 %/ºC a las frecuencias por encima de 100 Hz y aumenta con una velocidad media de 6.100 %/ºC a las frecuencias por debajo de 1 kHz.

REFERENCIAS

1.  República de Cuba. Ministerio de Salud Pública. Dirección Nacional de Registros Médicos y Estadísticas de Salud. "Anuario Estadístico de Salud 2017". 2018:65.

2.  Trujillo M, Berjano E. Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation. International Journal of Hyperthermia. 2013;29(6):590-7.

3.  Rossmann C, Haemmerich D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Critical Reviews™ in Biomedical Engineering. 2014;42(6).

4.  Tang J. Unlocking potentials of microwaves for food safety and quality. Journal of food science. 2015;80(8):E1776-E93.

5.  Van der Sman R. Model for electrical conductivity of muscle meat during Ohmic heating. Journal of Food Engineering. 2017;208:37-47.

6.  Roth CJ, Yoshihara L, Ismail M, Wall WA. Computational modelling of the respiratory system: discussion of coupled modelling approaches and two recent extensions. Computer Methods in Applied Mechanics and Engineering. 2017;314:473-93.

7.  Wang J-R, Sun B-Y, Wang H-X, Pang S, Xu X, Sun Q. Experimental study of dielectric properties of human lung tissue in vitro. Journal of Medical and Biological Engineering. 2014;34(6):598-604.

8.  Rigaud B, Morucci J-P, Chauveau N. Bioelectrical impedance techniques in medicine part I: bioimpedance measurement second section: impedance spectrometry. Critical Reviews™ in Biomedical Engineering. 1996;24(4-6).

9.  Gabriel C, Peyman A, Grant E. Electrical conductivity of tissue at frequencies below 1 MHz. Physics in medicine & biology. 2009;54(16):4863.

10.  Peyman A, Gabriel C, Grant E. Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics. 2007;28(4):264-74.

11.  Arrhenius S. On the reaction velocity of the inversion of cane sugar by acids. Zeitschrift fur physikalische Chemie. 1889;4:226ff.

12.  Diller KR, Pearce JA. Issues in modeling thermal alterations in tissues a. Annals of the NEW YORK Academy of Sciences. 1999;888(1):153-64.

13.  Macchi EG, Gallati M, Braschi G, Persi E. Dielectric properties of RF heated ex vivo porcine liver tissue at 480 kHz: measurements and simulations. Journal of Physics D: Applied Physics. 2014;47(48):485401.

14.  Haemmerich D, Ozkan O, Tsai JZ, Staelin ST, Tungjitkusolmun S, Mahvi DM, et al. Changes of electrical resistivity of swine liver after occlusion and postmortem. Medical & Biological Engineering & Computing, 2002;40:29-33.

15.  Gabriel S, Lau R, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Physics in medicine & biology . 1996;41(11):2271.

16.  IFAC: An Internet resource for the calculation of the dielectric properties of body tissues in the frequency range10 Hz-100 GHz,1997-2013. Available from: http://niremf.ifac.cnr.it/tissprop/16.  .

17.  Yero DD, González FG, Van Troyen D, Vandenbosch GA. Dielectric Properties ofEx VivoPorcine Liver Tissue Characterized at Frequencies Between 5 and 500 kHz When Heated at Different Rates. IEEE Transactions on Biomedical Engineering. 2018;65(11):2560-8.

18.  Deás Yero D, Gilart González F, Van Troyen D, Vandenbosch GA. Modelación de la ablación térmica por RF teniendo en cuenta la dependencia de las propiedades del tejido con la temperatura. Ingeniería Electrónica, Automática y Comunicaciones. 2019;40(1):81-95.

19.  Presman A. Electromagnetic fields and life: Springer Science & Business Media; 2013.

Recibido: 15 de Febrero de 2019; Aprobado: 03 de Septiembre de 2019

^*Autor Correspondiente: Roberto Vázquez Somoza, email: [e-mail]

No existe conflicto de intereses entre los autores, ni con ninguna institución a la que cada uno está afiliado, ni con ninguna otra institución.

Roberto Vázquez Somoza: Contribución importante en la realización del diseño de la instalación experimental, las mediciones, la revisión bibliográfica, la redacción del borrador del artículo y su versión final.

Fidel Gilart González: Contribución en la idea y diseño de la instalación experimental y al ajuste y procesamiento de los resultados de las mediciones, revisión del borrador y la versión final del artículo.

Ramón González Couso: Contribución en la interpretación desde el punto de vista médico-biológico de los resultados de las mediciones, análisis de la anatomía y fisiología del pulmón de cerdo, revisión del borrador y la versión final del artículo.

Roberto Vázquez Somoza, Ingeniero en Telecomunicaciones, Máster en Ingeniería Biomédica, Universidad de Oriente, Centro Nacional de Electromagnetismo Aplicado, Santiago de Cuba, Cuba, E-mail: [e-mail]. Sus principales intereses de investigación son los efectos térmicos de los campos electromagnéticos de radiofrecuencia sobre los tejidos biológicos, así como las aplicaciones industriales y médicas de los campos electromagnéticos, incluyendo el diseño, la modelación y las simulaciones.

Fidel Gilart González, Licenciado en Física, Doctor en Ciencias Físicas, Universidad de Oriente, Cuba, Centro Nacional de Electromagnetismo Aplicado, Santiago de Cuba, Cuba, E-mail: [e-mail]. Sus principales intereses de investigación son la interacción entre la radiación electromagnética no ionizante y los sistemas biológicos, así como las aplicaciones industriales y médicas de los campos electromagnéticos, incluyendo el diseño, la modelación y las simulaciones.

Ramón González Couso, Doctor en Medicina, Especialista de Segundo Grado en Cirugía, Instituto Superior de Ciencias Médicas Santiago de Cuba, Cuba, Hospital General “Juan Bruno Zayas”, Santiago de Cuba, Cuba, E-mail: [e-mail]. Sus principales intereses de investigación están relacionados con la morbilidad y mortalidad en las cirugías torácica específicamente las vinculadas a cáncer de pulmón, tumores de la pared torácica, cirugía esofágica, tumores mediastínicos, neumotórax y trauma torácico.