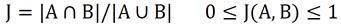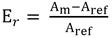Introducción
El cambio en el área de una lesión a lo largo del tiempo es un indicador importante para supervisar el proceso de cicatrización, evaluar la efectividad del tratamiento aplicado y, por consiguiente, diferenciar entre las lesiones que responden o no a dicho tratamiento [1]. Existen diferentes obstáculos que dificultan el poder alcanzar una elevada precisión al determinar el área real de una lesión en la piel. Es por esto que los investigadores trabajan en la búsqueda de alternativas automatizadas que garanticen dicha precisión así como la eficiencia en las mediciones. Actualmente, la evaluación clínica de lesiones cutáneas se centra principalmente en la inspección visual de un especialista que aproxima el área de la lesión al producto entre la longitud y la anchura que se obtienen al medirla manualmente con una regla o un pie de rey, sin tener en cuenta los cambios en su forma, generalmente irregular [2]. Alternativamente, se emplea el trazado con un rotulador en láminas cuadriculadas de acetato o película transparente, que se colocan sobre las lesiones para estimar sus áreas según el número de cuadros que contienen [3]. De la subjetividad de estos métodos se derivan mediciones imprecisas y poco fiables. Además, la cantidad de trabajo y tiempo que requieren por parte de los analistas, es otro gran problema. A ello se une que es necesario el contacto con la región dañada, lo cual puede no solo contaminar las lesiones y provocar futuras infecciones [4], sino también poner en riesgo la salud de los analistas que realizan las mediciones. El Procesamiento Digital de Imágenes (PDI) posee recursos para el monitoreo de las lesiones y la extracción automática de información valiosa que propician la reducción de errores de estimación y no requieren contacto con la lesión, basta con procesar una imagen digital de esta [5, 6, 7].
Existen varios espacios de color para examinar y aprovechar la información presente en una imagen digital y, aunque el espacio de color RGB es el más utilizado, cada modelo tiene un campo específico de trabajo y fortalezas [8]. Para el desarrollo de algoritmos de PDI orientados a tratar lesiones en la piel se prefieren modelos, como el HSV, que describen el color de forma análoga a como lo percibe el ojo humano, donde la crominancia es más importante que la percepción global del color. El modelo HSV, que caracteriza el color en términos de matiz (hue), saturación (saturation) y valor de intensidad (value) [9], se adapta a los requerimientos de esta investigación, ya que la componente V es independiente de la información de crominancia representada por las componentes de color: H y S.
La segmentación de las lesiones, dígase detección y delimitación de sus contornos, es una tarea previa y esencial en el procesamiento de imágenes clínicas de lesiones en la piel, ya que de su éxito depende la exactitud en la medición del área. Ninguna lesión, por parecida que parezca, es igual a otra en forma, tamaño y coloración; por lo que a pesar de los esfuerzos de la comunidad científica por desarrollar mejores algoritmos de segmentación, ninguno es generalmente aplicable a todas las imágenes ni igualmente adecuado para cualesquiera aplicaciones [10, 11, 12]. Resulta fundamental la evaluación de la calidad de los resultados de la segmentación con un algoritmo determinado, para decidir sobre la posible aplicación de este en un problema dado.
Para dar solución a esta necesidad y contribuir a la evaluación de fármacos candidatos que se desarrollan en el Centro de Bioactivos Químicos (CBQ) de la Universidad Central “Marta Abreu” de Las Villas, se evalúa estadísticamente el comportamiento de cinco métodos diferentes de segmentación por umbralado en imágenes a color de lesiones pertenecientes a ratones de laboratorio, infectados con protozoarios del género Leishmania. Los métodos de umbralado se adaptan bien a la detección de lesiones en la piel [13] y poseen una complejidad computacional relativamente baja, lo que les confiere una gran relevancia en esta investigación. La segmentación se lleva a cabo en el plano S de las imágenes, luego de ser transformadas al espacio HSV.
En la literatura se han definido algunos criterios de evaluación y propuesto diferentes métricas para cuantificar la calidad del resultado de la segmentación [14] [15]. En dependencia de si se requiere o no información previa sobre los objetos a reconocer, se puede hablar de métodos supervisados y no supervisados. La comparación directa entre el resultado que se obtiene de la segmentación y el resultado esperado, en este caso una segmentación realizada por expertos humanos, se considera que proporciona una evaluación más precisa [16]. En esta investigación, además de otras variables cuantitativas que se analizan, se utiliza como métrica de calidad el coeficiente de Jaccard con el objetivo de validar el grado de similitud entre las imágenes de referencia, segmentadas por expertos humanos, y las segmentadas mediante técnicas de PDI. Adicionalmente, se emplea la prueba de Friedman para realizar un análisis estadístico no paramétrico en busca de diferencias estadísticamente significativas entre los cinco métodos aplicados en la segmentación de las lesiones y comparar los resultados con los de la estadística descriptiva. Asimismo, se propone como alternativa para determinar el área de las lesiones, promediar las áreas resultantes de la segmentación de dos métodos diferentes: el método que tiende a sobrestimar y el que tiende a subestimar con el menor error relativo. Este estudio tiene una aplicación directa en la evaluación de los procesos de cicatrización y del tratamiento aplicado en úlceras, heridas y lesiones en la piel de forma general. Se incluye al respecto una prueba preliminar del método en la evaluación del área de úlceras del pie diabético, a partir de la cual se analizan las limitaciones y posible necesidad de adecuaciones del método descrito en este trabajo.
El resto del artículo sigue el orden siguiente: en la sección de materiales y métodos se explica la metodología propuesta para la segmentación de las lesiones y la extracción de indicadores de la calidad de dicha segmentación; en la de resultados y discusión se evalúa la fidelidad de los métodos aplicados y se muestran y analizan estadísticamente los resultados obtenidos; y finalmente se dan las conclusiones a las que estos resultados permiten arribar.
Materiales y métodos
Bases del modelo propuesto
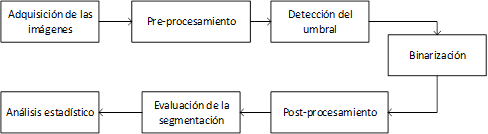
En esta investigación fueron analizadas 30 imágenes correspondientes a lesiones cutáneas practicadas en ratones de laboratorio, localizadas específicamente en la región dorsal del animal. La base de datos de imágenes se construyó con la ayuda de un dispositivo celular marca Samsung que posee una resolución máxima de 13 Mpx (4128x3096). Esta tarea de adquisición de las imágenes fue desarrollada por expertos en el área biológica del CBQ, al igual que la segmentación manual de las lesiones que fueron tomadas como referencia para posteriormente evaluar la calidad de la segmentación automática. El orden de ejecución de las etapas que se siguieron en la investigación se encuentra representado en la Fig. 1.
Para el desarrollo de los algoritmos implementados se utilizó el software Matlab en su versión R2015a, específicamente de su caja de herramientas Image Processing Toolbox[17] en la que se encuentra la documentación correspondiente al procesamiento, análisis, visualización y desarrollo de algoritmos para el tratamiento de imágenes. El IBM SPSS versión 25 se empleó para analizar estadísticamente los resultados de la segmentación mediante la prueba de Friedman e interpretar varios indicadores de calidad, a saber: coeficiente de Jaccard, error relativo promedio y desviación estándar en las mediciones.
Segmentación de las lesiones
Para reducir los errores en la detección de las lesiones, ya que el fondo y otros objetos presentes en las imágenes complejizaban la detección, antes de iniciar la segmentación fue necesario acondicionar las imágenes a tratar. Cada imagen se recortó, como muestra el ejemplo de la Fig. 2, a un área más cercana de la región de interés (ROI), la cual contenía tanto la lesión como piel sana adyacente a ella.
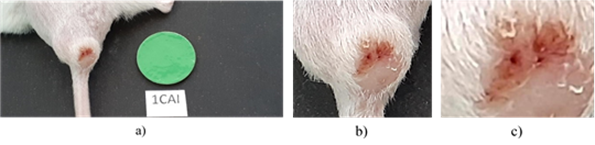
Fig. 2 a) Imagen original de 4128x1908 píxeles b) Una selección más pequeña de la imagen de 773x729 píxeles c) Una selección más pequeña con la ROI de 350x299 píxeles.
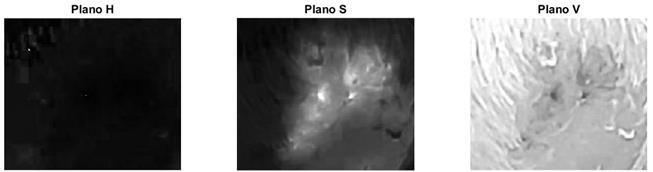
Como las lesiones tienden a tener coloraciones rojizas y en el plano S del modelo HSV se corresponden con zonas brillantes, como se aprecia en la Fig. 3, fue preciso el cambio de las imágenes del espacio RGB al HSV. Estas modificaciones resultaron ideales para la detección basada en umbrales que se realizó teniendo en cuenta la información del histograma del plano de saturación de las imágenes en el espacio HSV.
La detección automática del umbral y la posterior segmentación se llevaron a cabo siguiendo el patrón que se describe en la Fig. 4. Las funciones de Matlab programadas en [18] se utilizaron para la estimación de umbrales por cinco métodos diferentes de segmentación: Otsu [19], Iterativo [20], Kapur [21], Dempster [22] y Prewitt [23].
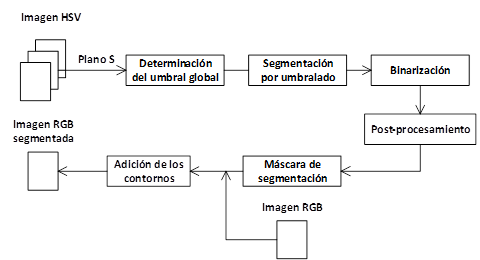
Fig. 4 Diagrama del algoritmo seguido para la segmentación de las lesiones por cada uno de los métodos seleccionados.
De la segmentación se obtuvieron imágenes binarias que fueron sometidas a varios procesos morfológicos para: 1) eliminar la presencia de “huecos”, es decir, píxeles pertenecientes a regiones de la piel dañadas pero que fueron excluidas de la selección; y 2) eliminar los elementos del fondo, de áreas más pequeñas que las lesiones, que no formaban parte de las zonas afectadas y aun así se encontraban seleccionados. De esta etapa de post-procesamiento se obtuvieron las máscaras de segmentación para evaluar los resultados de cada método con respecto a las segmentaciones de referencia. Adicionalmente, mediante un proceso de erosión, se extrajeron los contornos de dichas máscaras de segmentación y se mostraron los resultados de la segmentación de las imágenes a color en el espacio RGB a partir de insertar en estas los contornos mediante una operación de adición.
Indicadores de calidad de la segmentación
Para validar los algoritmos de segmentación aplicados, primeramente se determinó el grado de acierto entre la segmentación que se obtuvo por cada uno de los algoritmos implementados y la referencia de la que se disponía. La métrica seleccionada fue el coeficiente de Jaccard, definido por la expresión (1), donde |*| denota la cardinalidad del conjunto entre barras, para el cual se establecieron como indicadores de calidad los mostrados en la Tabla 1.
Tabla 1 Restricciones de calidad para evaluar la segmentación a partir de los valores del coeficiente de Jaccard.
| Intervalos | Calidad |
|---|---|
| 0 - 0,65 | Baja |
| 0,65 - 0,85 | Media |
| 0,85 - 1 | Alta |
Otra variable que se tuvo en cuenta para analizar la calidad de la segmentación fue el cálculo del error relativo en la medición del área de las lesiones, como supone (2):
donde Am representa el área que se obtiene de la segmentación automática por cada uno de los métodos aplicados y Aref, el área de referencia que se obtiene de la imagen de referencia correspondiente, ambas en píxeles. El signo de este error relativo sirvió para clasificar y agrupar los métodos en métodos que sobrestimaban, si en su mayoría tendían a sobrestimar (signo positivo), y métodos que subestimaban, si en su mayoría tendían a subestimar (signo negativo). Para incorporar al análisis los resultados de posibles mediciones manuales, se determinó por la misma expresión el error que podía cometerse al aproximar el área medida en píxeles de la lesión a la de un rectángulo circunscrito a esta (bounding box). La técnica utilizada incorporó en el campo de las fotos de las lesiones una figura geométrica de área conocida (el círculo verde en la Fig. 2), fácil de segmentar con exactitud, con la finalidad de disponer de las dimensiones físicas de un píxel sin necesidad de controlar la distancia a la cual se toma la foto.
Con el objetivo de seleccionar los métodos más precisos, para cada método de segmentación se promediaron los valores absolutos de los 30 errores relativos calculados, uno por cada imagen analizada. Seguidamente se promediaron las áreas de los dos mejores métodos, es decir, de aquellos métodos que según la clasificación dada sobrestimaban y subestimaban con los menores errores relativos promedio. El procedimiento de calcular los errores relativos y el error promedio con los valores absolutos de dichos errores relativos, se repitió también con el método de las áreas promedio mencionado anteriormente, con el objetivo de someterlo a análisis como una nueva propuesta en la búsqueda de la mejor precisión en las mediciones. La desviación estándar se tomó como un indicador de calidad adicional en cada uno de los casos descritos anteriormente para la medición de las lesiones.
Adicionalmente, para explorar la efectividad de los métodos de segmentación aplicados en esta investigación en otras posibles aplicaciones, se evaluó el desempeño de dichos métodos en una base de datos disponible con imágenes de lesiones cutáneas pertenecientes a úlceras del pie diabético con sus respectivas imágenes de referencia [24, 25, 26].
Pruebas no paramétricas
Para evaluar los resultados obtenidos de la segmentación e interpretar los indicadores de calidad que se definieron y calcularon, se realizó un análisis estadístico no paramétrico empleando la prueba de Friedman con pruebas post hoc. La prueba de Friedman se seleccionó, de entre posibles opciones para comparar las distribuciones de variables relacionadas, porque no requiere un gran volumen de datos ni probar la normalidad de los mismos. Con esta prueba, para cada caso, a las k variables se les asignaron rangos de 1 a k para posteriormente calcular el rango promedio de cada variable y construir los estadísticos de prueba. Así, el método con mejores valores de coeficiente de Jaccard fue el de mayor rango promedio; contrario a los casos en que el indicador fue el error relativo en la medición del área de las lesiones, donde el mejor método fue el de menor rango promedio. Lo que sucede es que para cada imagen analizada, el método de mejor coeficientes de Jaccard fue el que más próximo a 1 tuvo su valor y, por tanto, recibió el mayor valor en el rango; mientras que el método de menor error en las mediciones fue el de menor valor de error y recibió el menor valor en el rango. En los casos en que se determinó que existían diferencias estadísticamente significativas, se utilizaron pruebas post hoc de 2 muestras relacionadas para comparar el método de mejor rango promedio de la prueba de Friedman con el resto. Para ello se utilizó la corrección de Bonferroni, con la que se ajustó el nivel de significación por el hecho de que se realizaron varias comparaciones. Para seleccionar y recomendar el mejor método de segmentación se aplicaron diferentes pruebas de hipótesis en busca de diferencias estadísticas entre las posibles alternativas.
Resultados y discusión
Evaluación de resultados en la medición de lesiones cutáneas en ratones de laboratorio
En la detección de las lesiones en la piel se obtuvieron resultados de baja, media y alta calidad, según los indicadores propuestos para el coeficiente de Jaccard en la Tabla 1. La Tabla 2 recoge cuantitativamente los resultados de la segmentación de 10 de las 30 imágenes de muestra, en términos del coeficiente de Jaccard. En ninguna de las imágenes segmentadas coincidió que con los cinco métodos utilizados se obtuvo una segmentación de alta calidad. Al promediar los coeficientes de Jaccard obtenidos por la segmentación para cada uno de los métodos, el método Iterativo arrojó los mejores resultados para un indicador de 0,717. Lo siguieron Otsu, con 0,706 de promedio, y Kapur, con 0,704. Los métodos de peor comportamiento resultaron ser Dempster y Prewitt con índices de 0,678 y 0,632, respectivamente.
Tabla 2 Coeficientes de Jaccard calculados para 10 de las imágenes segmentadas.
| Imagen | Otsu | Iterativo | Kapur | Dempster | Prewitt |
|---|---|---|---|---|---|
| caja 1 CPD-1-.jpg | 0,849 | 0,867 | 0,861 | 0,876 | 0,841 |
| caja 1 AD-1-.jpg | 0,769 | 0,751 | 0,737 | 0,695 | 0,717 |
| caja 1 AI-1-.jpg | 0,680 | 0,639 | 0,645 | 0,588 | 0,060 |
| caja 1 C AD-1.jpg | 0,801 | 0,787 | 0,856 | 0,687 | 0,841 |
| caja 1 C-1-.jpg | 0,719 | 0,695 | 0,731 | 0,736 | 0,750 |
| caja 1 CAD-1.jpg | 0,806 | 0,851 | 0,822 | 0,680 | 0,889 |
| caja 1 CAI-1-.jpg | 0,841 | 0,518 | 0,838 | 0,365 | 0,424 |
| caja 1 CAI-PI-1.jpg | 0,884 | 0,798 | 0,878 | 0,881 | 0,861 |
| caja 1 CAIPI-1-.jpg | 0,774 | 0,820 | 0,786 | 0,844 | 0,780 |
| caja 4 CPD-1.jpg | 0,611 | 0,620 | 0,646 | 0,577 | 0,601 |
Análoga a la Tabla 2, la Tabla 3 recoge el área obtenida de la segmentación para cada uno de los métodos aplicados y la correspondiente a la segmentación de referencia, todas expresadas en píxeles. Con la totalidad de estos valores de área se determinaron los errores relativos resultantes de las diferentes segmentaciones automáticas.
Según el signo de los errores relativos calculados en la medición del área para cada uno de los métodos, los métodos Otsu, Kapur y Prewitt se clasificaron en métodos que tienden a subestimar; mientras que el Iterativo y Dempster, en métodos que tienden a sobrestimar. Los mejores de cada clasificación resultaron ser Otsu e Iterativo, con valores promedio de los errores cometidos (valores absolutos) de 0,218 y 0,210, respectivamente. Un caso interesante resulta, por ejemplo, la imagen “caja 1 AI-1-.jpg”, donde el error relativo obtenido por el método Iterativo (-0,144) es menor modularmente que el obtenido por el método Otsu (0,145) y, sin embargo, en la Tabla 2 se muestra que el coeficiente de Jaccard para esta imagen es superior por el método Otsu, lo que supone una mejor segmentación de la lesión. Lo que sucede es que el coeficiente de Jaccard se ve afectado por la posición de las regiones que se comparan y no solo por sus dimensiones, como sí ocurre en la determinación del error en el cálculo del área.
Tabla 3 Áreas en píxeles de las segmentaciones automáticas y la referencia para 10 de las imágenes segmentadas.
| Imagen | Otsu | Iterativo | Kapur | Dempster | Prewitt | Referencia |
|---|---|---|---|---|---|---|
| caja 1 CPD-1-.jpg | 72332 | 87124 | 79464 | 89224 | 71066 | 82557 |
| caja 1 AD-1-.jpg | 10628 | 12723 | 8897 | 14457 | 8374 | 10247 |
| caja 1 AI-1-.jpg | 23030 | 30821 | 19099 | 43825 | 1608 | 26932 |
| caja 1 C AD-1.jpg | 3951 | 5727 | 4335 | 6908 | 4228 | 4813 |
| caja 1 C-1-.jpg | 15652 | 22268 | 16702 | 20319 | 18396 | 18696 |
| caja 1 CAD-1.jpg | 28148 | 38506 | 29105 | 49434 | 35724 | 33711 |
| caja 1 CAI-1-.jpg | 27239 | 48882 | 25728 | 69814 | 60117 | 25497 |
| caja 1 CAI-PI-1.jpg | 14923 | 18499 | 15667 | 15597 | 16315 | 15742 |
| caja 1 CAIPI-1-.jpg | 82260 | 88576 | 83560 | 107782 | 82894 | 105733 |
| caja 4 CPD-1.jpg | 5212 | 9291 | 5622 | 4919 | 5127 | 8532 |
Por otra parte y como era de esperar, al seleccionar el área de las lesiones con un rectángulo para simular el proceso de medición manual, se tendió a sobrestimar en las mediciones de las dimensiones de las lesiones porque se incluyó piel sana en las selecciones. Como resultado de estas mediciones manuales se cometieron errores que, en la mayoría de los casos, resultaron desfavorables frente a los que se cometieron al tomar como medida aproximada del área el promedio de las áreas calculadas por los métodos de Otsu e Iterativo. Incluso, dicha aproximación reflejó menores errores que los de cada método por separado. Ello también se corroboró con los valores de la desviación estándar de los errores que se encuentran, junto con los errores calculados, agrupados en el gráfico de la Fig. 5.

Fig. 5 Valores promedio de los errores relativos cometidos (valor absoluto) en la medición del área de las lesiones y la desviación estándar de dichos errores. Las estadísticas del área promediada se calculan con el promedio de las áreas en píxeles de los métodos de Otsu e Iterativo.
Al aplicar la prueba de Friedman a los coeficientes de Jaccard se obtuvieron los rangos promedio que se muestran en la Tabla 4, donde se ubicó al método Iterativo como el mejor, seguido por Kapur y Otsu en ese orden. Sin embrago, se determinó que no existen diferencias estadísticamente significativas entre los métodos, ya que se trabajó con un nivel de significación de p=0,05 y los resultados arrojaron una significación asintótica mayor, p=0,062. El hecho de que la diferencia entre el umbral de significación (p=0,05) y el valor obtenido (p=0,062) sea muy pequeña, sugiere que la escala de rangos promedio puede aún tener utilidad para la comparación entre los métodos.
Tabla 4 Prueba de Friedman: rangos, coeficientes de Jaccard
| Método | Rango promedio |
| Iterativo | 3,55 |
| Kapur | 3,30 |
| Otsu | 2,88 |
| Dempster | 2,82 |
| Prewitt | 2,45 |
| Nota: Rangos promedio de la prueba de Friedman para determinar el método con mejores coeficientes de Jaccard. | |
De igual forma, se aplicó la prueba de Friedman a los valores absolutos de errores relativos obtenidos para cada método en la medición del área de las lesiones. Como resultado, existieron diferencias estadísticamente significativas entre ellos, ya que el nivel de significación (p=0,015) fue menor que el establecido (p=0,05). Se rechazó entonces la hipótesis nula de que no existían diferencias entre los métodos aplicados. Los rangos promedio que se muestran en la Tabla 5 ubicaron al método Iterativo en la primera posición, seguido por Kapur y Otsu en ese orden. En la Fig. 6 se proyectan las segmentaciones por estos tres métodos en una de las imágenes de estudio.
Tabla 5 Prueba de Friedman: rangos, errores relativos (valor absoluto).
| Método | Rango promedio |
|---|---|
| Iterativo | 2,25 |
| Kapur | 2,77 |
| Otsu | 3,13 |
| Dempster | 3,30 |
| Prewitt | 3,55 |
| Nota: Rangos promedio de la prueba de Friedman para determinar el método con menores errores relativos en las mediciones de las áreas de las lesiones. | |
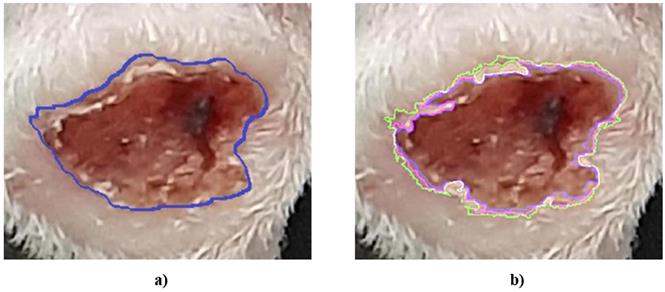
Fig. 6 Segmentación de la lesión en una de las imágenes de estudio, realizada a) manualmente por un experto (referencia) b) de forma automática por los métodos Iterativo (verde), Kapur (magenta) y Otsu (azul).
El análisis anterior se complementó con una prueba post hoc de los rangos con signos de Wilcoxon, para comparar dos muestras relacionadas. El método Iterativo, el de mejor rango promedio, se pareó con los métodos restantes teniendo en cuenta la corrección de Bonferroni con la que se ajustó el intervalo de confianza a 0,01. Como refleja la Tabla 6, dicha prueba arrojó resultados estadísticamente significativos para los casos Dempster-Iterativo y Prewitt-Iterativo, puesto que en ambos casos el método Iterativo se mostró superior en las comparaciones.
Como los mejores resultados en la determinación del área de las lesiones se obtuvieron con los métodos Iterativo, Kapur y Otsu, a partir de analizar los rangos promedio, se realizó una nueva prueba de Friedman. En este último test se incluyeron, además de estos tres métodos, los otros dos métodos considerados en este trabajo para la medición de las lesiones, a saber: promedio de las áreas obtenidas por los métodos Iterativo y de Otsu (propuesto) y área determinada de forma manual (simulada).
Los resultados de la prueba de Friedman arrojaron que existían diferencias estadísticamente significativas entre algunos de los métodos analizados, para una significación asintótica de p=0,004. Se rechazó nuevamente la hipótesis nula, ya que se trabajó con un umbral de p=0,05. De la Tabla 7 se puede inferir que el método de promediar las áreas se posicionó como el mejor con el menor rango promedio, seguido por el método Iterativo.
Tabla 6 Estadísticos de prueba de rangos con signo de Wilcoxon, errores relativos (valor absoluto).
| Otsu-Iterativo | Kapur-Iterativo | Dempster-Iterativo | Prewitt-Iterativo | |
| Significación asintótica (bilateral) | 0,280 | 0,096 | 0,009 | 0,002 |
| Significación exacta (bilateral) | 0,287 | 0,097 | 0,008 | 0,001 |
| Significación exacta (unilateral) | 0,144 | 0,049 | 0,004 | 0,001 |
| Probabilidad en el punto | 0,002 | 0,001 | 0,000 | 0,000 |
| > | ||||
Tabla 7 Prueba de Friedman: rangos, errores en la medición del área (valor absoluto) por diferentes métodos.
| Métodos | Rango promedio |
|---|---|
| Área_prom | 2,17 |
| Iterativo | 2,75 |
| Área_BB | 3,08 |
| Kapur | 3,47 |
| Otsu | 3,53 |
| > | |
En la prueba post hoc de los rangos con signos de Wilcoxon, que se aplicó también a este análisis, el método de promediar las áreas se pareó con el resto en busca de diferencias estadísticamente significativas. Según la Tabla 8, la mayor diferencia estadísticamente significativa se obtuvo con el método Kapur, donde el método Áreas_prom se mostró muy superior en la comparación con este. A pesar de que en las comparaciones del método Áreas_prom con los métodos Otsu, Iterativo y Área_BB, la significación unilateral resultó superior al umbral que se estableció con la corrección de Bonferroni de 0,01, el método de promediar las áreas también fue superior en las comparaciones.
Tabla 8 Estadísticos de prueba de rangos con signo de Wilcoxon, errores en la medición del área (valor absoluto) por diferentes métodos.
| Otsu-Área_prom. | Iterativo-Área_prom. | Kapur-Área_prom | ÁreaBB-Área_prom | |
|---|---|---|---|---|
| Significación asintótica (bilateral) | 0,033 | 0,206 | 0,001 | 0,072 |
| Significación exacta (bilateral) | 0,033 | 0,213 | 0,000 | 0,073 |
| Significación exacta (unilateral) | 0,016 | 0,106 | 0,000 | 0,037 |
| Probabilidad en el punto | 0,001 | 0,004 | 0,000 | 0,002 |
| Nota: Búsqueda de diferencias estadísticamente significativas entre los métodos seleccionadas como mejores de las pruebas anteriores y dos métodos adicionales considerados en la investigación, con los errores relativos en las mediciones de las áreas de las lesiones como indicador. | ||||
El análisis estadístico no fue concluyente para determinar la mejor alternativa para calcular el área de las lesiones, sobre todo porque no se encontraron diferencias estadísticamente significativas entre la alternativa de promediar las áreas de los métodos Otsu e Iterativo y el método Iterativo. Haciendo un balance entre los resultados recogidos en la Tabla 8, los errores cometidos en la medición de las lesiones por cada método y la Fig. 5, estos sugieren que el promedio de áreas de los métodos de Otsu e Iterativo pudiera ser superior, por lo que sería recomendable realizar un análisis estadístico con un mayor número de imágenes para llegar a conclusiones definitivas al respecto.
Resultados en el experimento con imágenes de úlceras del pie diabético
En el estudio realizado con la base de datos de imágenes de úlceras del pie diabético [24-26] se obtuvieron resultados satisfactorios en la segmentación de una parte de la base de datos. Dichos resultados se ilustran al considerar una muestra de 25 imágenes seleccionadas, las cuales se eligieron de manera tal que fueran favorables para el sistema propuesto, dado que el mismo no fue concebido para este tipo de imágenes. En la Tabla 9 pueden observarse los coeficientes de Jaccard obtenidos para 10 de las imágenes procesadas. Se muestran solo los resultados de aplicar los métodos Otsu, Iterativo y Kapur por ser los de mejor desempeño. La Fig. 7 ilustra un ejemplo de estos resultados.
Tabla 9 Coeficientes de Jaccard calculados para 10 de las imágenes segmentadas con úlceras del pie diabético.
| Imagen | Otsu | Iterativo | Kapur |
|---|---|---|---|
| 100019.jpg | 0,838 | 0,838 | 0,842 |
| 100021.jpg | 0,863 | 0,862 | 0,841 |
| 100032.jpg | 0,889 | 0,888 | 0,841 |
| 100036.jpg | 0,905 | 0,906 | 0,904 |
| 100040.jpg | 0,880 | 0,808 | 0,796 |
| 100045.jpg | 0,843 | 0,828 | 0,836 |
| 100050.jpg | 0,867 | 0,858 | 0,842 |
| 100054.jpg | 0,880 | 0,886 | 0,893 |
| 100063.jpg | 0,936 | 0,915 | 0,920 |
| 100085.jpg | 0,830 | 0,839 | 0,834 |

Fig. 7 Segmentación de úlceras del pie diabético en tres imágenes diferentes, realizada de forma automática por los métodos Iterativo (verde), Kapur (magenta) y Otsu (azul), en las que se logra aislar aceptablemente el área de la lesión.
La Tabla 10 muestra el área estimada en la segmentación de las 10 imágenes, recogidas en la Tabla 9, así como la correspondiente a la referencia de dichas imágenes, todas expresadas en píxeles. Como puede observarse, la tendencia de los métodos aplicados fue a subestimar en la medición del área de las lesiones.
Tabla 10 Áreas en píxeles de las segmentaciones automáticas y la referencia para 10 de las imágenes segmentadas con úlceras del pie diabético.
| Imagen | Otsu | Iterativo | Kapur | Referencia |
|---|---|---|---|---|
| 100019.jpg | 3360 | 3360 | 3068 | 3219 |
| 100021.jpg | 2261 | 2257 | 2180 | 2563 |
| 100032.jpg | 8604 | 8601 | 8534 | 9621 |
| 100036.jpg | 5287 | 5193 | 5379 | 5601 |
| 100040.jpg | 21994 | 20190 | 19875 | 24855 |
| 100045.jpg | 2988 | 2898 | 2938 | 3392 |
| 100050.jpg | 8617 | 8515 | 8337 | 9840 |
| 100054.jpg | 5993 | 6056 | 6126 | 6779 |
| 100063.jpg | 44657 | 43343 | 43657 | 47019 |
| 100085.jpg | 1819 | 1922 | 1848 | 2074 |
Con los valores de áreas de las 25 imágenes analizadas se determinaron los errores relativos resultantes de las segmentaciones automáticas por los métodos Otsu e Iterativo. En la Fig. 8 se muestran los promedios de estos errores junto a los que se cometieron al promediar las áreas calculadas por los métodos Otsu e Iterativo, para tomar dicho promedio como medida aproximada del área. Esta aproximación reflejó menor error promedio que el obtenido con el método Otsu, pero no fue mejor que el alcanzado con el Iterativo.
En la Fig. 9 pueden observarse algunos de los casos en los que el uso de los algoritmos programados no fue efectivo al emplearlos en la segmentación de la base de datos de úlceras del pie diabético. Como se explicó antes, la segmentación utilizando estos algoritmos no fue configurada para este tipo de imágenes (úlceras del pie diabético). Para la adquisición de las imágenes de la leishmaniasis en ratones, se plantearon determinadas exigencias en el laboratorio en cuanto al enfoque a determinada distancia y a condiciones de iluminación (intensidad y color) que se diferencian de las presentes en esta base de datos de diabetes. Además de que en esta última aparecen lesiones diferentes en coloración, ya que pueden estar infestadas o presentar tejido necrosado. También afecta la segmentación los diferentes tonos de color de piel en los pacientes y estar presentes varias lesiones a segmentar en una misma imagen.

Fig. 8 Valores promedio de los errores relativos cometidos (valor absoluto) en la medición del área de las úlceras del pie diabético y la desviación estándar de dichos errores. Las estadísticas del área promediada se calculan con el promedio de las áreas en píxeles de los métodos de Otsu e Iterativo.
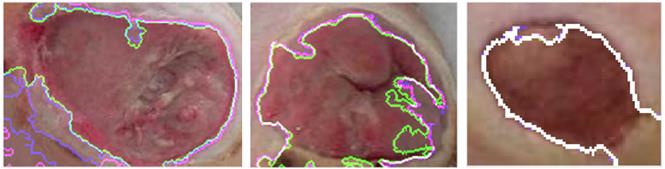
Fig. 9 Segmentación de úlceras del pie diabético en tres imágenes diferentes, realizada de forma automática por los métodos Iterativo (verde), Kapur (magenta) y Otsu (azul), en las que no se logra aislar adecuadamente el área de la lesión.
No obstante, el hecho de que en un conjunto de imágenes de la base de datos de úlceras del pie diabético se obtenga una buena segmentación, sugiere que el algoritmo creado es capaz de funcionar en este tipo de lesiones si se observan determinadas reglas a la hora de la adquisición de las imágenes y se realizan ajustes en la programación, tema que puede ser objeto de estudios futuros.
Conclusiones
En este estudio se han analizado estadísticamente varios métodos de segmentación por umbral con el propósito de estimar, con una precisión satisfactoria, las áreas de lesiones en la piel. La alternativa de promediar las áreas de los métodos Otsu e Iterativo y el propio método Iterativo, resultaron superiores en las diferentes comparaciones con el resto de los métodos según la estadística descriptiva y pudieran incorporarse a una herramienta computacional para medir las áreas de lesiones en la piel con resultados fiables. Aunque las pruebas no paramétricas no arrojaron diferencias estadísticamente significativas que permitan afirmar categóricamente la superioridad de algún método específico, el promedio de áreas de los métodos de Otsu e Iterativo pudiera ser la mejor propuesta de las consideradas en esta investigación. Para investigaciones futuras se recomienda procesar un mayor número de imágenes que permitan ampliar el análisis y definir la mejor alternativa.
Los resultados ofrecidos en la Sección 3 pueden tener una influencia significativa en el campo de la evaluación y el diagnóstico de lesiones en la piel, sobre todo porque sugieren que las mediciones automáticas de las lesiones tienden a mejorar la precisión con respecto a las aproximaciones manuales de un especialista, aunque en este caso tampoco se encuentran diferencias estadísticamente significativas. Como existe una gran variabilidad en las mediciones manuales que se utilizaron como referencia para la evaluación supervisada de las diferentes segmentaciones, producto de la experiencia y criterio del especialista encargado, sería recomendable estimar cuantitativamente cuan variables son dichas mediciones. Los experimentos realizados con úlceras del pie diabético sugieren que los algoritmos de segmentación empleados en esta investigación pudieran ser elegibles para esta otra aplicación bajo determinadas condiciones de adquisición de las imágenes, tema que requeriría investigaciones posteriores.