INTRODUCCIÓN
Desde 2012 el currículo chileno se hace énfasis en que la enseñanza no sólo en contenido, sino también en habilidades y actitudes. La enseñanza del volumen comienza en el cuarto año básico (9 años), y es base para su enseñanza en cursos posteriores. En el programa de estudio correspondiente a este curso, el concepto de volumen está vinculado con objetivos que buscan conocer algunos cuerpos geométricos, describir algunas características y compararlos. Por su parte, el programa de sexto básico (11 años) espera que los estudiantes calculen el volumen de algunos cuerpos utilizando medidas estandarizadas. En los niveles posteriores se establecen como objetivos “Desarrollar las fórmulas para encontrar (...) el volumen de diferentes cuerpos” (Ministerio de Educación, 2012, p. 125) como el cilindro y prismas rectos, cono y esfera respectivamente, relacionando el volumen de algunos cuerpos con otros, como, por ejemplo, en el caso del volumen del cono con el volumen del cilindro.
En el año 2020, se reformula el currículo de los últimos cursos de Educación Secundaria. Se propone un curso electivo de geometría, que tiene entre sus objetivos “formular y verificar conjeturas acerca de la forma, área y volumen de figuras 3D, generadas por rotación o traslación de figuras planas en el espacio, incluyendo el uso de herramientas tecnológicas digitales.” (Ministerio de Educación, 2020, p. 39)
Los textos escolares son un reflejo de las directrices ministeriales, se observa, por ejemplo, que no existe una distinción entre el concepto de volumen y capacidad, lo cual genera que no se logre comprender a profundidad esta magnitud por parte de los estudiantes. Se plantean actividades dirigidas a calcular distintos volúmenes de cubos y paralelepípedos, o bien determinar alguno de sus lados teniendo la medida de sus aristas o el área de sus caras. De esta forma el tratamiento curricular del volumen se centra, en su mayoría, en el cálculo, haciendo que esta magnitud sea reducida al uso de fórmulas, lo que conlleva a una aritmetización del contenido (Chamorro, 2003).
Como estudiantes de último año de Licenciatura en Educación Matemática, se ha podido apreciar que las situaciones anteriormente planteadas son comunes en la enseñanza del volumen. Lamentablemente, se observa que todos los materiales y orientaciones al alcance del docente siguen reproduciendo prácticas algorítmicas, lejanas al pensamiento métrico y geométrico, donde la ausencia de reflexiones sobre las prácticas docentes son constantes.
Para el reconocimiento de problemas y la búsqueda de soluciones se requiere de la capacidad reflexiva de los profesores de su práctica, entendiendo a ésta última no solo como la aplicación de conocimientos, si no como “una actividad dinámica, reflexiva, que comprende los acontecimientos ocurridos en la interacción entre maestro y alumnos” (García, Loredo & Carranza, 2008, p. 4). Esto quiere decir, que la práctica en sí, no es algo que se limite simplemente al trabajo en el aula, ya que conlleva reflexiones previas y posteriores, que se orientan a partir de las creencias, conocimientos, valores y actitudes que posea el docente.
Por lo planteado anteriormente, se comprende la importancia de que el docente realice una práctica reflexiva, la que es necesaria desde la formación inicial, ya que servirá para que el futuro docente adquiera “la disposición reflexiva, así como la orientación hacia el aprendizaje permanente” (Tallaferro, 2006, p. 270) lo cual le permitirá enfrentar su realidad educativa de forma más consciente y crítica, lo que influirá en la toma de decisiones y acciones durante su labor docente.
Además, se observa que si bien, se realiza una adecuación curricular a la educación obligatoria, no se efectúan cambios en la formación inicial docente que consideren los elementos que han variado en cada eje. Por otra parte, en las universidades formadoras de profesores se trabaja con énfasis en objetos matemáticos y elementos desde el ámbito pedagógico, pero estos no necesariamente se relacionan, como es el caso del concepto de conservación del volumen, que se aborda sicológicamente, sin embargo, no se vincula con los cursos de geometría (Comisión Nacional de Acreditación, 2016). Por último, durante la formación universitaria no es común conocer o trabajar con materiales y recursos didácticos, lo que conlleva un deficiente conocimiento sobre recursos para la enseñanza, tanto del volumen como de otros objetos matemáticos.
Es por esto que, al idear una clase para tratar los objetivos de enseñanza de primero medio, y de acuerdo al contexto anteriormente expuesto, surge la siguiente pregunta ¿Qué conocimiento especializado es adecuado movilizar para enseñar el volumen en el aula de Educación Secundaria?
Para abordar el tratamiento del concepto de volumen en la escuela, es necesario tener conocimientos acerca de esta magnitud y los diversos significados que puede tener: como el espacio que ocupa un cuerpo o como la cantidad de unidades que lo forman, también como el espacio desplazado o como espacio encerrado (Sáiz, 2003).
Respecto a las propiedades de esta magnitud, una de gran importancia es la de conservación, que hace referencia a la capacidad que tiene el volumen de un cuerpo de permanecer constante, a pesar de que la forma de dicho cuerpo cambie. Esto se puede observar en un experimento realizado por Piaget & Inhelder (1971), en el cual, al manipular dos bolitas de masa moldeable, de la misma forma y peso, se aplasta una o bien se deforma una, concluyendo que los niños tienen la creencia de que al variar la forma del cuerpo en estudio varía también su volumen.
Por otra parte, el concepto de volumen mantiene una estrecha relación con el concepto de capacidad, el cual se entiende como “espacio vacío con posibilidad de ser llenado” (Del Olmo Moreno & Gil, 2007, p. 9). A diferencia del volumen, esta magnitud solo la poseen algunos cuerpos, como por ejemplo un estadio y un bolso, los que poseen tanto volumen como capacidad, en cambio un espejo y una goma de borrar no poseen capacidad, pero sí volumen, debido a que estos no pueden contener otro objeto, pero sí ocupan espacio.
A su vez, el volumen es tratado en otras áreas, como química o física, por lo que la comprensión del concepto también se ve influenciada por estos factores, lo que genera confusiones para su adquisición. Esto permite tener una visión más profunda o amplia para su enseñanza y aprendizaje, evidenciando su complejidad y por consiguiente su tratamiento.
El volumen puede tratarse como una magnitud que puede ser abordada desde dos aspectos, como una magnitud unidimensional y como una magnitud tridimensional. (Del Olmo et al., 2007, p. 108). La primera “es una medida producto de tipo directo” (Chamorro, 2003, p. 246), utilizando la comparación, la evaluación, estimación, y demás; mientras que la magnitud tridimensional hace referencia al producto de sus medidas, esto es, en el caso del volumen la multiplicación de sus tres dimensiones. Esto hace que el tratamiento del volumen sea más complejo y que por lo tanto sea necesario trabajar ambos aspectos minuciosamente, de modo que estos tengan relación, para poder comprender de esta forma el concepto.
Con lo anterior, es fundamental determinar qué conocimientos posee el docente para la enseñanza del volumen de forma que propicie el aprendizaje de los estudiantes. Para indagar sobre estos conocimientos que tiene el docente de matemática, nos centraremos en las ideas planteadas inicialmente por Shulman, quien es reconocido como pionero en los estudios del conocimiento profesional del profesor.
Shulman (1986) centra sus investigaciones en los tipos de conocimientos y destrezas necesarias para la enseñanza, estableciendo un nuevo enfoque a las investigaciones sobre docencia, que integra el conocimiento pedagógico con el conocimiento disciplinar, describiendo el conocimiento pedagógico del contenido (PCK) como uno de los conocimientos fundamentales que el docente debe poseer para hacer posible la enseñanza, el cual “Representa la mezcla entre contenido y pedagogía por la que se llega a una comprensión de cómo determinados temas y problemas se organizan, se representan y se adaptan a los diversos intereses y capacidades de los alumnos y se exponen para su enseñanza”. (p. 175)
Este conocimiento pedagógico del contenido da cuenta de la necesidad de desarrollar un conocimiento especializado del profesor. Ball, Thames & Phelps (2008) centran su estudio en el conocimiento matemático necesario para la enseñanza que debe tener el docente del área, “analizando la naturaleza del conocimiento matemático y cómo este puede ayudar en la enseñanza” (Rojas, 2014, p.49).
En esta investigación se utiliza un modelo teórico basado en la propuesta de Shulman (1986) y Ball et al. (2008), el Mathematics Teachers’ Specialised Knowledge (MTSK), que considera el conocimiento especializado como conocimiento particular del profesor de Matemática.
Este modelo tiene como propósito ser una herramienta para el análisis del conocimiento de los docentes de Matemática, es un “marco analítico para comprender mejor el conocimiento del profesor de Matemática (qué conoce, cómo, qué le posibilita, qué necesita)” (Climent, Escudero, Rojas, Carrillo, Muñoz & Sosa, 2014, p.43). De esta forma, podemos organizar el conocimiento del profesor de Matemática, como una propuesta teórica y a la vez como una herramienta metodológica que permite analizar la práctica pedagógica.
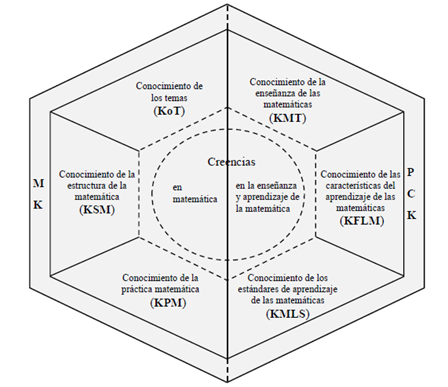
En la figura 1 se puede apreciar la estructura del MTSK y los subdominios que posee este modelo. Se observan dos grandes ejes, el conocimiento matemático (MK) y el conocimiento pedagógico del contenido (PCK), los cuales a su vez poseen tres subdivisiones cada uno.
En este estudio los autores han tomado en consideración cuatro subdominios del MTSK: El dominio del tema (Knowlege of Topic, [KoT]), el conocimiento de las características del aprendizaje de la matemática (Knowledge of Features of Learning Mathematics [KFLM]); el dominio de la didáctica de la matemática (KMT) y el conocimiento de los estándares de aprendizaje de la matemática (Knowledge of Mathematics Learning Standards [KMLS]).
El dominio del tema (Knowlege of Topic, [KoT]) se refiere al conocimiento del contenido de la disciplina que el profesor debe movilizar, como conceptos, proposiciones, propiedades, clasificaciones, ejemplos, entre otros. En el caso del volumen, un profesor de enseñanza media, debe conocer la definición del concepto y las diversas interpretaciones que se le otorgan, conocer las fórmulas utilizadas para calcular el volumen de un cuerpo conocido, determinar el volumen a partir de una ecuación particular, conociendo algunas dimensiones de este cuerpo, midiendo el desplazamiento del agua al sumergir un cuerpo en este líquido, teniendo en consideración que este cuerpo debe ser compacto. También debe conocer diferentes formas de representar el volumen de un cuerpo junto con las notaciones matemáticas utilizadas, como conocer la relación entre el volumen del cilindro y del cono, además algunas propiedades que posee este concepto, como por ejemplo que al cambiar de forma un cuerpo mantiene su volumen.
El conocimiento de las características del aprendizaje de la matemática (Knowledge of Features of Learning Mathematics [KFLM]); hace referencia a el “conocimiento que tiene el profesor sobre las características del contenido matemático en sí mismo como objeto de aprendizaje” (Escudero, 2015, p. 297), las cuales son producto de la relación entre el contenido matemático y el estudiante, para esto el docente debe conocer de antemano el modo de pensar del alumno respecto a las tareas matemáticas, las estrategias que utiliza, el lenguaje común que emplea al expresar un nuevo conocimiento matemático, conocer las fortalezas y dificultades que pueden generar el tratamiento de un contenido matemático y las preconcepciones respecto a algún tema.
En el caso del volumen, el uso indiscriminado de la fórmula, puede generar que los estudiantes resuelvan problemas mecánicamente, sin comprender el porqué de estos, también se encuentra la confusión entre los conceptos capacidad y volumen, y otras magnitudes. Además, posiblemente producto de la aritmetización de la geometría los estudiantes presentan una falta de interés en su aprendizaje.
El dominio de la didáctica de la matemática (KMT) se define como el “conocimiento del profesor sobre las características del contenido matemático como objeto de enseñanza; lo que el profesor sabe sobre las distintas posibilidades de enseñanza, condicionadas por la naturaleza misma del contenido” (Escudero, 2015, p. 301). En esta subdivisión se considera que el docente debe tener conocimiento de los recursos, materiales y las características que hacen de estos, propicios para la enseñanza de algún contenido matemático, esto es, “conocer los instrumentos que tiene disponibles para abordar el contenido, sus potencialidades, sus limitaciones y las repercusiones que tendría el usarlo como medio para presentar un contenido matemático” (Escudero, Contreras & Vasco, 2016, p.38).
Al trabajar en la sala de clases el concepto de volumen el docente puede diseñar la secuencia de los contenidos para trabajar dicha magnitud, basándose en la teoría de los niveles de Van Hiele. El conocimiento de los estándares de aprendizaje de la matemática (Knowledge of Mathematics Learning Standards [KMLS]) hace referencia a que el docente debe conocer lo que se plantea en el currículo escolar, es decir qué contenidos, habilidades y actitudes están acordes al nivel de enseñanza, de esta forma el docente debe tener “conocimiento acerca de lo que el estudiante debe/puede alcanzar en un curso escolar determinado” (Flores, Escudero & Aguilar, 2013, p. 84) y a lo largo del ciclo escolar.
Al momento de trabajar el volumen el docente debe tener en consideración en qué cursos o niveles este se trabaja y de las capacidades esperadas de los estudiantes en cada curso para comprenderlo. Por medio del MTSK, se pueden propiciar situaciones reflexivas que se direccionen a que el profesorado sea consciente de lo complejo de la práctica, sus creencias, conocimientos y competencias, adquiridas o potenciales, para un adecuado ejercicio docente. Por ello, es necesario asumir una actitud crítica y comprometida con su propio rol. Es por esto que, para la formación de un profesor reflexivo se requiere el perfeccionamiento continuo del docente mediante la reflexión para, en y sobre sus prácticas.
MÉTODOS
La naturaleza de esta investigación exige que sea de carácter cualitativo, ya que el objetivo es analizar el conocimiento profesional del profesor de Matemática sobre volumen en el currículo vigente, siendo el paradigma interpretativo el óptimo, dado que “existen múltiples realidades construidas por los actores en su relación con la realidad social en la cual viven” (Martínez, 2011, p. 6), siendo fundamental contemplar las interpretaciones de cada sujeto que participa activamente en la investigación.
Se busca caracterizar el conocimiento que tiene el docente de Matemática para la enseñanza del volumen, no con el único fin de conocerla, sino también transformarla, llevando a cabo una investigación-acción que se realiza en conjunto por dos docentes, una profesora universitaria formadora de docentes y un profesor en ejercicio, encargado de la asignatura de Matemática del curso en el cual se lleva a cabo la investigación y dos docentes en formación.
El curso en el que se lleva a cabo esta investigación, corresponde a primer año de Enseñanza Media (14 años), en el cual aproximadamente la mitad de los estudiantes del curso se encuentran en situación de discapacidad auditiva, por consiguiente, este curso trabaja en conjunto con el departamento de educación diferencial, mediante el proyecto de integración estudiantil, más conocido como PIE.
Debido a lo anterior es que, a la hora de hacer clases, se encuentran a cargo tres o cuatro personas, dos de los cuales están de forma constante durante el año, que corresponden al profesor de la asignatura y una profesora de diferencial. También de preferencia para la asignatura dos intérpretes, las que no poseen necesariamente conocimientos pedagógicos.
Para llevar a cabo esta investigación, se realizan planificaciones, ejecuciones y reflexiones de tres clases de 225 minutos de clases (5 horas pedagógicas). Para la recolección de información se utilizaron técnicas que sirven para la obtención de datos más detallados y espontáneos, por lo cual se recurrió a la grabación de audio y video, ya que este tipo de instrumento permite “observar y analizar los hechos repetidas veces” (Martínez, 2006, p. 138), dando la posibilidad de analizar las situaciones desde distintos puntos de vista y posiciones.
RESULTADOS
En este apartado se presentan algunas situaciones que ocurrieron durante las clases realizadas, las cuales serán analizadas con los subdominios del MTSK. Los diálogos transcurren entre las profesoras en formación (PF1, PF2), el profesor (P), la formadora de profesores (FP) y los estudiantes (E).
Episodio 1: Aritmetización
PF2: ¿Cuál creen que es el volumen de esta plasticina? de esta barrita de esta plasticina. ¿No se les ocurre cómo medirlo?
E1: Sacando el volumen del cilindro, sacando el radio.
PF2: ¿Sacando el radio de esta pequeña circunferencia? ¿Hay una forma más fácil?
P: Por ejemplo, en 4to básico, nunca calcularon el volumen de una piedra
E: No
PF2: ¿Alguno que quiera medir cuánto volumen tiene la plasticina?
FP: Paremos un poquito…. Por ejemplo ¿saben cuánto es un cm cúbico? […] ¿Cuánto físicamente?
E1: 1x1x1
En este episodio se puede evidenciar que los estudiantes, al preguntarles por el volumen de la plasticina, buscaron utilizar la fórmula del cilindro, lo que demuestra que asocian inmediatamente el volumen al uso de fórmulas, dado que es lo que conocen y a lo que se le ha dado énfasis durante su formación, debido a que se aritmetiza la medida.
La profesora en formación es consciente de esto y plantea una actividad en la que no se recurra al uso de fórmulas o procedimientos mecanizados, de forma que se relacionen con el contenido desde otra perspectiva. Con lo anterior es posible ver cómo se vinculan el conocimiento de las características del aprendizaje de la matemática (KFLM) y el dominio de la didáctica de la matemática (KMT) ya que la docente en formación plantea una actividad en la cual guía a los estudiantes con una secuencia a seguir, buscando darle un nuevo significado al concepto abordado.
Se observa que, es probable, que los estudiantes de primero medio no han tratado el volumen, en sus años anteriores, fuera del trabajo de fórmulas o cubos. Si es observable que no tienen referencias sobre unidades de medida volumen o sobre mediciones como la inmersión en un vaso graduado con agua, para cuerpos irregulares. Es común que, al planificar, sobre todo en los primeros años de ejercicio docente, se espera que los estudiantes posean los conocimientos respecto a los estándares de aprendizaje de las matemáticas (KMLS), sin contextualizar que a veces, no es acorde al nivel de enseñanza en el que se encuentran. De esta forma, el trabajo se modifica y se realizan actividades correspondientes a cuarto año básico, que no fueron simples para los estudiantes que operan formalmente. Asimismo, se observa que existen unos 6 años de desfase curricular. Se intenta, de esta forma, subsanar el trabajo mecánico y aritmetizado, mediante un experimento en el cual se utiliza plasticina, con la que se puede construir cuerpos regulares e irregulares, lo cual nos da posibilidad de medir el volumen de dicho cuerpo sin el uso de fórmulas, siendo este un material apropiado para la comprensión del concepto. Con lo anterior se van creando los referentes que se necesitan para poder enseñar volumen a estudiantes de primero medio.
Episodio 2: Conservación del volumen:
Al momento de investigar el entorno de la enseñanza del volumen se observa una sugerencia de actividad para abordar la percepción del concepto de volumen y el comportamiento de esta magnitud. Se propone estudiar el comportamiento del volumen del globo a partir de algunas intervenciones, situación que hizo cuestionar qué pasaba con la conservación del volumen del globo al inflarse. Se recurrió posteriormente a plantear la duda a la formadora de profesores, la que menciona lo complejo que es para los estudiantes comprender esta conservación.
Este episodio genera ciertas dificultades en las profesoras en formación, ya que, según su percepción, el volumen del globo varía, situación que contradecía con el conocimiento que tenían acerca de la conservación del volumen, generando un conflicto sobre el dominio del tema (Knowlege of Topic, [KoT]. Luego al conversar con la formadora de profesores, se resuelven algunas dudas concluyendo que es la capacidad del globo la que varía, pero su volumen es el mismo. A raíz de ello, el objeto en sí, varía de volumen. Se comenta sobre la complejidad del trabajo del volumen y su conservación, y que es trivializada en la formación de profesores de matemática.
De esta forma, se evidencia como el dominio del tema (Knowlege of Topic, [KoT] se va modificando a medida que se investiga y reflexiona sobre diversas actividades planteadas.
Episodio 3: Intérpretes
Durante las clases realizadas, grabadas en video, se puede observar que en la sala hay tres o cuatro personas a parte del docente, cada una desempeña roles distintos, ellas se dedican a trabajar con los estudiantes con necesidades educativas especiales, por lo general hay una educadora de diferencial y dos intérpretes, siendo estas últimas el vínculo existente entre el docente de Matemática, el objeto matemático y los estudiantes sordos. Durante las clases se puede observar dos señas que significan volumen.
Es conocido que la lengua de señas no es de carácter universal, ya que si el concepto no se encuentra consensuado se genera una seña para definirlo y utilizarlo, debido a que deletrearlo es agotador y muy extenso. Es por esto que muchos conceptos son establecidos en la sala de clases, dándose una relación estrecha entre la intérprete y estudiantes, es decir, existe una forma única de expresarse entre ellos.
Durante las clases se pudo apreciar que las intérpretes se dedicaban a enseñar a los estudiantes sordos, de manera que existe una comunicación solamente entre ellos, por lo que el docente de la asignatura no conoce necesariamente lo que las educadoras comunican o explican a los educandos. En este caso, no se puedo saber si el contenido está siendo interpretado de forma idónea por los estudiantes, pues al no conocer la lengua de señas, no se tienen las herramientas que permitan ser parte de la interacción.
Es por lo anteriormente planteado que tiene relevancia la idea que posea la intérprete que se encuentre en la clase sobre cómo explicar lo que está enseñando el docente, lo cual dependerá de sus conocimientos sobre el contenido matemático a tratar, es decir del dominio del tema (Knowlege of Topic, [KoT] de la intérprete. De igual forma debe tener conocimiento acerca de las características del aprendizaje del contenido matemático y de su enseñanza.
DISCUSIÓN
La formación académica del docente es para trabajar con estudiantes de 12 años o mayor. Al reflexionar sobre la enseñanza del volumen, se observó que la conservación trajo bastantes complicaciones. Hubo dudas sobre la conservación en el globo, se discutió varias veces desde miradas matemáticas y didácticas, porque según el conocimiento adquirido, el volumen no variaba, pero según la idea y percepción sí lo hacía. Luego de aclarar las ideas, se consideró una actividad interesante a trabajar, pero se sentía que faltaba preparación para enseñarlo, por lo que la formadora de docentes fue la que lideró la actividad. Posterior a ello, sí se consideró existía la preparación para realizar la clase. Pocas veces se observa que un docente formador realice clases junto a futuros profesores sobre problemáticas que los últimos encuentran. Se considera que estas prácticas deberían ser habituales.
En el Episodio 1, se observa una aritmetización de la geometría en el sistema escolar, posiblemente porque se busca resolver problemas para responder con pruebas estandarizadas que le dan prioridad al uso de fórmulas y no a la apropiación de referentes de unidades de medida o a la estimación de magnitudes.
Este excesivo uso de fórmulas, junto con la consideración de que el volumen se mide en unidades cúbicas es un lugar común en los textos escolares, e incluso, los programas de estudios ministeriales. A su vez, la formación de profesores es lejana a la escuela, lo que tiene como consecuencias no trabajar con materiales óptimos para la enseñanza. Usar estos materiales en la práctica sin tener conocimiento en la formación docente es complejo, porque no hay familiaridad, es por esto que sería ideal que las asignaturas disciplinares de la formación de profesores de matemática estén enfocados en la práctica docente.
La aritmetización presente en el tratamiento del volumen, genera obstáculos didácticos, epistemológicos y ontogénicos (Brousseau, 1989). Los dos primeros ocurren debido a que los estudiantes no logran comprender las referencias y la conservación, haciendo que sea aún más complejo comprender lo que sucede con el globo, ya que necesita de ambos (conservación y referentes, porque no hay uso de fórmula con este objeto) siendo una actividad en la que se busca netamente comprender qué sucede con el objeto. El tercer obstáculo se produce debido a la madurez de los estudiantes, ya que según lo que plantea Piaget & Inhelder (1971) los estudiantes desarrollan la conservación entre los 6 a 11 años, lo cual se evidencia que no ocurre en el curso de primer año medio.
En el curso en que se realizó la investigación se encontraba una intérprete que trabajaba exclusivamente con los estudiantes sordos. Durante todas las clases, ella interpretaba a los estudiantes, especialmente cuando los docentes intervenían directamente. A la vez, la intérprete comunicaba las dudas o comentarios que estos estudiantes tenían, por lo que la interacción con los estudiantes no era directa. Esto generaba que no se tuviera un conocimiento acerca de cómo los estudiantes interactuaban con el objeto matemático y cuáles eran sus dudas o dificultades. Si bien se intentó generar instancias en las que los estudiantes sordos participaran, se pudo percibir que no fueron suficientes, ya que, en las últimas clases, dedicadas específicamente al cálculo de volumen, manifestaron algunas dudas en torno a la compresión del concepto de volumen, objetivos que se trabajaron en las primeras clases. Esto demuestra que no se poseen herramientas que permitan trabajar con estos estudiantes, en parte porque en la formación inicial no se desarrollan competencias para el trabajo con estudiantes con necesidades educativas especiales y además no se dimensiona el complejo trabajo que esto conlleva.
CONCLUSIONES
El estudio realizado demuestra, por una parte, la naturaleza del proceso pedagógico, en el que intervienen tanto el dominio del contenido de las ciencias exactas como el de sicología, la pedagogía y la didáctica. En particular el abordaje del concepto de volumen en la escuela ilustra la necesidad de profundizar en las relaciones entre el conocimiento matemático y la didáctica.
Los episodios descritos en este artículo permiten concluir que la práctica docente es compleja, por lo tanto, su reflexión es fundamental para el desarrollo profesional. Si la universidad y la escuela se potencian, logran un desarrollo profesional bidireccional que beneficia tanto a formadores de profesores y en mayor medida, a futuros profesores, como en el caso de este estudio, en el que es evidente que tuvo lugar un aprendizaje colaborativo.