Introducción
A partir de un diagnóstico al proceso de enseñanza - aprendizaje de la Matemática III de los estudiantes de la carrera Ingeniería Informática de la Universidad del Minint se determinaron las problemáticas siguientes: predomina un aprendizaje reproductivo o memorístico en los estudiantes; las orientaciones metodológicas de la asignatura Matemática III carecen de precisiones didácticas que favorezcan un aprendizaje desarrollador en los estudiantes; falta de integración de saberes para la solución de problemas vinculados al modelo del profesional; además del limitado empleo de las tecnologías para favorecer el aprendizaje de los estudiantes.
Ante tal situación, el investigador elabora una estrategia didáctica como alternativa para el aprendizaje desarrollador de la Matemática III en los estudiantes de la carrera Ingeniería Informática con perfil Informática Operativa.
Dicha estrategia se sustenta en los fundamentos teóricos y los principios expuestos, y tiene los siguientes componentes esenciales: de cambio.
El presente artículo expone el diseño de la estrategia para el aprendizaje desarrollador de la Matemática III en los estudiantes de la carrera Ingeniería Informática y los principales resultados de su aplicación.
Desarrollo
La estrategia didáctica posee los siguientes sustentos teóricos: lógicos, pedagógicos, didácticos y psicológicos; los cuales se sintetizan a continuación. Los fundamentos filosóficos parten de la filosofía marxista - leninista y tienen su base en la Lógica, donde se toma en consideración la comprensión de González (2008), de entender la Lógica en su integración. De este modo, el autor comparte que, “todo aquello que sea resultado de la actividad pensante del hombre es portador de fundamentos lógicos” (p. 96), estableciendo la relación directa entre el pensamiento y los sustentos de la Lógica como ciencia.
Desde este referente y en correspondencia con los objetivos de la investigación, se adscribe al entendimiento desde esta perspectiva del aprendizaje desarrollador de la matemática. Se asumen dos presupuestos lógicos fundamentales: la especificidad del conocimiento objeto de estudio (Contenido) y las exigencias lógicas. (Leyes y principios).
Los fundamentos psicológicos que se asumen provienen del Enfoque Histórico - Cultural, especialmente aquellos principios y categorías que se vinculan a las particularidades del aprendizaje. En este sentido se resalta el carácter activo del sujeto y la Zona de Desarrollo Próximo (ZDP). También se comparten los análisis de Vygotski en torno a la relación entre Pensamiento y Lenguaje y sobre la formación de conceptos. Se asumen elementos de la Teoría de la formación de las acciones mentales, propuesta por P. Ya. Galperin.
Los fundamentos pedagógicos se sustentan en la tendencia pedagógica Enseñanza Desarrolladora y su concepción del proceso educativo donde se otorga un rol activo a los actores del proceso. Además, toma en consideración principios pedagógicos como la vinculación del estudio con el trabajo y el principio de la unidad de la instrucción y la educación (Horroutinier, 2006); y se rescatan un conjunto de características como la proyección social, la orientación humanística y el carácter transformador necesario en todo proceso educativo, que se expresan en la interrelación de los pares categoriales instrucción - educación, o en procesos como la enseñanza y la formación.
Los fundamentos didácticos que sustentan la estrategia, se ubican en una concepción desarrolladora, reconociéndose el carácter activo de los actores del proceso de enseñanza - aprendizaje; así como su determinación histórico - social. Presenta una novedosa visión de la interrelación existente entre los componentes del proceso: objetivos, contenidos, métodos, medios, formas de organización y evaluación, donde el estudiante adopta un rol protagónico en el proceso y se aborda desde las potencialidades de los actores del mismo. Se propone una enseñanza donde se parta de las experiencias previas del estudiante y el profesor con el contenido, implicando no solo la esfera cognitiva sino la afectividad que se produce del contacto directo con el fenómeno estudiado, y que a su vez favorezca el desarrollo del pensamiento lógico. De ahí la importancia de considerar el ofrecimiento de apoyos a los estudiantes, que le permita al profesor orientar su influencia pedagógica hacia lo potencial.
En correspondencia se asumen un conjunto de principios: principio del carácter científico, principio del proceso enseñanza-aprendizaje desarrollador y principio del carácter colectivo de la enseñanza (Silvestre Oramas & Zilberstein Toruncha, 2002).
La implementación de la estrategia está soportada en la utilización de las TIC, por lo que se hace necesario estudiar la relación del hombre con los objetos. Esta, según el desarrollo de la cultura, está influida por la mediación instrumental (signos y herramientas) y la mediación social (la relación con los otros).
Los signos “son aquellos estímulos que tienen una función dada en la comunicación y que pueden materializarse mediante señales o símbolos”. (Castro, 1986, p. 33). El papel de estos mediadores es “gobernar los procesos de actuación humana. Con el auxilio de estos signos el hombre dirige y ejecuta las operaciones lógicas para solucionar tareas”. (Delgado, 2004, p. 12).
Los signos y herramientas, como mediadores, están presentes durante todo el proceso de realización del trabajo dentro de un entorno virtual. A través de ellos los profesores asimilan un nuevo lenguaje y lo utilizan en su modo de actuar para incorporarlos a los procesos de trabajo del colectivo de asignatura de Matemática III.
Desde el punto de vista sociológico, el aprendizaje desarrollador de los estudiantes se logra cuando se aprovechan las potencialidades de la comunicación entre los sujetos que participan en esta actividad. No solo entre el profesor y los estudiantes, sino entre los estudiantes propiamente.
Componentes y estructura de una estrategia didáctica para el aprendizaje desarrollador de la Matemática III en los estudiantes de la carrera Ingeniería en Informática con perfil Informática Operativa
Objetivos a alcanzar
La estrategia tiene objetivo general: “Contribuir a un proceso de enseñanza - aprendizaje desarrollador de la Matemática III en la carrera Ingeniería Informática con perfil Informática Operativa, mediante su reordenamiento didáctico y metodológico, y la implementación de procedimientos docentes que estimulen el desarrollo de las habilidades del pensamiento lógico”.
Para dar cumplimiento al objetivo general, se plantean como objetivos específicos:
Organizar didáctica y metodológicamente la asignatura Matemática III para establecer vínculos coherentes y sistémicos entre sus componentes didácticos, en función de la orientación del proceso de enseñanza - aprendizaje al logro del aprendizaje desarrollador de sus contenidos por los estudiantes.
Implementar procedimientos dirigidos a la estimulación del desarrollo de las habilidades del pensamiento lógico de los estudiantes y de los procesos que intervienen en el aprendizaje desarrollador de la Matemática III, en función de la formación integral para toda la vida de los oficiales del MININT.
Principios didácticos que la sustentan
La estrategia didáctica se sustenta en los postulados generales de un proceso de enseñanza - aprendizaje que instruya, eduque y desarrolle, por lo que se definen como principios didácticos los siguientes:
Carácter desarrollador de la enseñanza de la matemática.
Se pone de manifiesto cuando el estudiante juega un papel activo en la actividad, existe una motivación intrínseca por el aprendizaje, el reconocimiento de sus carencias y fortalezas para lograr el objetivo propuesto, la formulación de metas propias de aprendizaje, la identificación de las necesidades para alcanzar las metas, la elección e implementación de las estrategias de aprendizaje adecuadas, y la realización de un proceso de autoevaluación de los resultados de este.
Integración con enfoque de sistema de los componentes didácticos de la asignatura.
Se logra cuando el estudiante se involucra en la búsqueda del conocimiento matemático desde posiciones activas. Se transita desde un proceso de enseñanza aprendizaje centrado en el profesor, a un proceso de enseñanza - aprendizaje en el que el estudiante tenga un papel protagónico, lo que implica que deje la posición pasiva dentro de la clase de Matemática III y cambie a una posición activa en cada una de las etapas de su actividad cognoscitiva, valorativa y práctica, desde la orientación hasta el control, determinando por sí mismo bajo la dirección del profesor, las estrategias de aprendizaje a utilizar para la aprehensión de los conceptos, propiedades y procedimientos matemáticos.
Para ello, el profesor debe estimular en el estudiante, el desarrollo de diferentes formas de razonamiento, revelar relaciones, hacer síntesis y esquemas lógicos.
Atención a las diferencias individuales en el desarrollo de los estudiantes, en el tránsito del nivel logrado hacia el que se aspira.
Este principio se ve favorecido en la estrategia didáctica en cuanto a los resultados del diagnóstico inicial, que arrojará las fortalezas, debilidades, las potencialidades y dificultades presentes en el estudiante, para lo cual el profesor debe tomar en cuenta la ayuda para buscar las respuestas adecuadas que promuevan su desarrollo. Esto exige la elaboración de tareas y/o ejercicios matemáticos diferentes y variados y la orientación de tareas que propicien el desarrollo del pensamiento lógico.
Vínculo del contenido del aprendizaje con la práctica social.
El mismo se refleja en la estrategia con la intención de establecer relaciones dialécticas entre el conocimiento sensorial y el conocimiento racional, lo que permite el ascenso a una práctica integradora que propicia la cientificidad en el trabajo que se realiza. Este principio aboga por lograr que el estudiante aprenda desde la práctica y para la práctica, contextualizando socialmente el contenido matemático y evitando todo tipo de pronunciación exclusivamente teórica en las clases de matemática.
La estrategia didáctica diseñada, se caracteriza por ser:
Flexible: Puede ser aplicada a diferentes asignaturas de la disciplina Matemática Superior, siempre que se respeten las invariantes elaboradas por el autor para profesores universitarios, ajustándose a las particularidades de los diferentes profesionales en formación.
Contextual: Está enmarcada y fue elaborada en un contexto histórico - social concreto, por lo que responde a las características del contexto cubano en particular y a las características y exigencias propias de la universidad cubana.
Desarrolladora: Está orientada a la estimulación del desarrollo potencial del estudiante. Mediante el proceso de enseñanza - aprendizaje, se contribuye al aprendizaje desarrollador de la matemática desde las dimensiones activación - regulación, significatividad y motivación. La estrategia se apoya en la utilización de las TIC como medio que propicia el vínculo de los estudiantes con el modelo del profesional desde la enseñanza de la matemática.
Etapas y acciones a desarrollar
La estrategia consta de cuatro etapas: Diagnóstico, Planificación, Ejecución y Control, las que a su vez están integradas por acciones con el objetivo de conducir un proceso de enseñanza - aprendizaje desarrollador de la Matemática III.
Dada la relación dialéctica entre las etapas de la estrategia didáctica, el carácter sistémico que le resulta inherente garantiza una complementación, de forma tal, que no es necesario que culmine una etapa en particular, para dar inicio a cualquiera de las otras (Fig. 1).
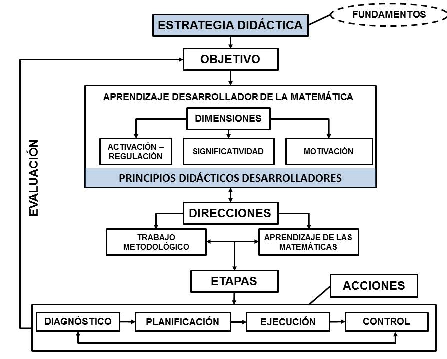
Fig. 1 - Estrategia didáctica para el aprendizaje desarrollador de la Matemática III en la carrera Ingeniería Informática.
Se asume la importancia de conducir el proceso de enseñanza - aprendizaje a partir de una concepción desarrolladora, lo que implica, por un lado, la reconceptualización por parte del profesor acerca de sus componentes, y por otro, que estos logren que las dimensiones que caracterizan esta concepción se manifiesten durante el proceso de enseñanza - aprendizaje.
El planteamiento del objetivo debe ir dirigido a alcanzar niveles superiores de desarrollo de la personalidad del estudiante. Para su orientación se desarrollan acciones en torno a qué aprender, cómo aprender y para qué aprender, lo que significa determinar los conocimientos y habilidades que deben ser aprendidos en las clases, los métodos de enseñanza - aprendizaje y la intencionalidad educativa de los contenidos.
Se emplean métodos predominantemente productivos como la búsqueda parcial o heurística, investigativo, creativo, discusión, situaciones, juego de roles o simulación; sin que se obvie la necesaria interacción de estos con los métodos reproductivos como el explicativo - ilustrativo, dando un enfoque sistémico a los mismos, de manera que se promueva la participación activa, reflexiva y consciente de los estudiantes, con lo que se garantiza no solo la aprehensión del contenido, sino su problematización, valoración y aplicación.
Todo ello dirigido a garantizar la individualidad desde el trabajo grupal, la comunicación y el trabajo cooperado, a fin de estimular las motivaciones intrínsecas. Deben permitir el perfeccionamiento de los modos de actuar en los estudiantes al influir en el desarrollo de habilidades relacionadas con la orientación, la planificación, el control y la evaluación de esta actividad, aspectos que potencian además la autorregulación.
Los medios de enseñanza como soporte material del método están encaminados no solo a desarrollar el elemento cognitivo sino el volitivo, afectivo y conductual de los estudiantes. El papel de los medios de enseñanza está (además de presentar al estudiante la realidad objetiva o sus representaciones materiales más concretas cuando no están al alcance del profesor) en proporcionar verdaderamente el puente o vínculo entre estas percepciones concretas y los procedimientos lógicos del pensamiento, estimulando estos últimos.
Se toman en consideración los sistemas implícitos en los contenidos: conocimientos, hábitos y habilidades, experiencias de la actividad creadora y normas de relación con el mundo; con el objetivo de que los profesores posean claridad de que el contenido permite instruir y al mismo tiempo educar al estudiante para contribuir a su formación integral, durante el proceso de enseñanza - aprendizaje.
Un componente esencial del proceso de enseñanza - aprendizaje, es la evaluación, ya que parte del planteamiento de los objetivos y concluye con la determinación del grado de eficiencia del proceso, dado por la medida en que los profesores y estudiantes hayan logrado, con el resultado de su actividad, alcanzar los objetivos propuestos.
Para llevar a cabo el proceso evaluativo, se utilizan diferentes tipos de evaluación:
Heteroevaluación: Consiste en que una persona evalúa lo que otra ha realizado.
Co-evaluación: Es el tipo de evaluación que se concreta en la interacción y cooperación entre los sujetos que participan en el proceso, en llegar a un consenso entre el profesor y el estudiante. En este tipo de evaluación los implicados en el proceso son participantes de la evaluación con iguales posibilidades de emitir juicios sobre todos y cada uno de los aspectos evaluados.
Autoevaluación: Se concreta a un nivel cualitativamente superior en el que cada sujeto se evalúa a sí mismo. En la misma se involucran activamente todos los sujetos implicados en el mismo. Consiste en la evaluación que el estudiante hace de su propio aprendizaje y de los factores que intervienen en éste.
Meta evaluación: Consiste en que alguien que no ha participado en la evaluación evalúe la misma.
La co - evaluación, autoevaluación, heteroevaluación y metaevaluación transitan desde lo simple hasta lo complejo, de lo particular a lo general, así como la intervención oportunamente para que el estudiante busque, activamente, cómo resolver lo planteado. Su integración en un sistema coherente y armónico de evaluación contribuye al aprendizaje desarrollador por las potencialidades que cada una de ellas ofrece.
El proceso de enseñanza - aprendizaje se puede organizar de manera frontal, grupal, individual y colectiva. En ellas se garantiza el principio de uniformidad y activación individual que debe regir en este proceso para que se produzca una adecuada diferenciación dentro y fuera de la clase. Su adecuada estructuración garantiza el funcionamiento sistémico del proceso de enseñanza - aprendizaje haciéndolo a su vez desarrollador.
La orientación didáctica de la estrategia establece la necesidad de trabajar en dos direcciones principales: una dirigida al trabajo metodológico que deben desarrollar los profesores, responsabilizados con la impartición de la asignatura Matemática III; y la otra, enmarcada en las acciones que realizan los estudiantes para lograr el aprendizaje de las matemáticas, lo que da lugar a la integración propia que resulta inherente a la naturaleza didáctica del presente resultado científico.
La dirección del trabajo metodológico ha de sentar pautas sobre bases científicas que promuevan el empleo de los recursos didácticos desarrolladores. Ello significa establecer un compromiso que propicie, desde el proceso de enseñanza - aprendizaje, aprendizajes activos, reflexivos y conscientes por parte de los estudiantes, ofreciendo las ayudas pertinentes para garantizar la atención individual y colectiva de los mismos y el desarrollo de la planificación, ejecución y control del trabajo independiente que se realiza en las aulas y fuera de ellas. Lo anterior ha de proyectarse mediante el establecimiento de ambientes que promuevan el aprendizaje desde contextos afectivos y de colaboración.
En la dirección que aborda el aprendizaje de las matemáticas por los estudiantes, es necesario crear condiciones para que los mismos dispongan de suficiente libertad de participación en las clases, para formular preguntas, debatir y reflexionar ideas y puntos de vista, desarrollando estrategias de aprendizaje dirigidas fundamentalmente a la solución de problemas.
Lo anterior implica situar la ejercitación en un lugar prioritario en las clases de Matemática III, lo que crea las condiciones para el desarrollo de habilidades y hábitos, propios del trabajo matemático y llevar a cabo la socialización de los conocimientos y experiencias adquiridas, sobre la base de intercambios entre los estudiantes y entre estos y sus profesores.
Etapa 1: Diagnóstico.
Objetivo: Analizar el estado de los conocimientos - habilidades sobre conceptos, propiedades y procedimientos matemáticos de los estudiantes mediante un diagnóstico, además de las principales deficiencias que presenta el proceso de enseñanza - aprendizaje de la Matemática III.
Acción 1.1: Estudiar y analizar los documentos rectores del proceso de enseñanza - aprendizaje de la asignatura Matemática III de la carrera Ingeniería Informática con perfil Informática Operativa.
Se realiza un análisis de los documentos rectores del proceso de enseñanza - aprendizaje de la asignatura Matemática III tales como: Programas Analíticos de la Disciplina Matemática Superior y de la asignatura Matemática III, así como el Modelo del Profesional que permitan caracterizar el sistema de contenidos, los objetivos y las habilidades de la asignatura que posibilitan el aprendizaje desarrollador en función de favorecer el desarrollo de los modos de actuación del Ingeniero Informático con perfil Informática Operativa.
Acción 1.2: Identificar la situación en que se encuentra cada estudiante con relación a los contenidos básicos que debe dominar.
Se realiza un diagnóstico en el que se evalúan los contenidos precedentes: cálculo de límite y continuidad de funciones de una y varias variables, derivadas e integrales. Las preguntas poseen un balance adecuado de los niveles de desempeño cognoscitivo: reproductivas, de aplicación y preguntas que muestren el sentido de creatividad que pueden tener los estudiantes.
Los indicadores para evaluar los resultados del diagnóstico son los siguientes:
Realiza la búsqueda independiente de los conocimientos matemáticos y las vías a utilizar para lograrlos.
Resuelve tareas complejas con la utilización de procedimientos propios del pensamiento matemático.
Reflexiona acerca de la efectividad de las estrategias de aprendizaje utilizadas.
Expresa sus conocimientos precedentes y los relaciona con los nuevos conocimientos.
Resuelve tareas para la solución de problemas relacionados con la vida en las que aplica los conocimientos matemáticos.
Demuestra satisfacción e interés por aprender los contenidos matemáticos.
Muestra seguridad para enfrentarse a conflictos cognitivos y tomar decisiones.
Para llevar a cabo el diagnóstico inicial, se emplean las siguientes vías y procedimientos:
En la primera clase de la asignatura, mediante el diálogo e intercambio (previsto por el profesor) con los estudiantes. El profesor insertará al diálogo conceptos elementales de la matemática que se emplean en las materias de las asignaturas precedentes (Matemática I y II), tales como: límite, continuidad, derivada e integral. Este procedimiento permite adquirir una valoración preliminar del estado del conocimiento y las habilidades del pensamiento de los estudiantes.
Para precisar esta información se aplicará una prueba pedagógica que permita medir los conocimientos de matemática iniciados en las asignaturas Matemática I y II, relacionados con: el cálculo de límites y continuidad de funciones de una y varias variables, principales propiedades de las derivadas y cálculo integral. Se realizarán preguntas a los estudiantes que permitan medir la aplicación de estos contenidos al modelo del profesional. Se sugiere la orientación de problemas donde exista la necesidad de aplicar dichos contenidos.
Acción 1.3: Identificar la preparación de los profesores para lograr un aprendizaje desarrollador en los estudiantes.
Se realiza observación a clases y se aplica una encuesta a los profesores para obtener las principales fortalezas y debilidades que poseen para lograr un aprendizaje desarrollador en los estudiantes.
Acción 1.4: Realizar reunión metodológica para abordar las principales fortalezas y debilidades detectadas en el diagnóstico referidas al aprendizaje desarrollador de la matemática.
Mediante esta acción se retroalimenta a los profesores sobre las principales fortalezas y debilidades detectadas en el diagnóstico inicial a los estudiantes, las encuestas a docentes y las observaciones a clases.
Etapa 2: Planificación.
Objetivo: Planificar las actividades que se ejecutarán en el proceso de enseñanza - aprendizaje de la Matemática III para contribuir al aprendizaje desarrollador de sus contenidos.
Acción 2.1: Realizar actividades metodológicas para dirigir el proceso de enseñanza - aprendizaje de la Matemática III.
Acción 2.1.1: Reunión metodológica en el colectivo de año para aprobar las actividades metodológicas a desarrollar.
Las actividades metodológicas estarán dirigidas a:
Diseñar tareas interdisciplinarias que posibiliten el tránsito a niveles de independencia cognoscitiva en estos estudiantes, desde distintas perspectivas y el apoyo mancomunado de los profesores.
Evaluar el estado del aprendizaje de los estudiantes durante el transcurso de la asignatura.
Acción 2.1.2: Reunión metodológica del colectivo de disciplina Matemática Superior para aprobar el plan de trabajo metodológico del colectivo de asignatura Matemática III.
El plan elaborado estará dirigido a:
Impartición de conferencias científicas por especialistas, referidas al aprendizaje desarrollador de la matemática, sus rasgos, dimensiones e indicadores.
Realización de un taller científico metodológico encaminado al estudio de los métodos productivos para la enseñanza de la matemática, el que incluye la presentación de soluciones por los profesores.
Acción 2.1.3: Desarrollar un sistema de clases metodológicas: instructivas, demostrativas y abiertas.
Para orientar a los profesores y demostrar en la práctica los principales elementos definidos en la estrategia didáctica y los cambios que implica en el desarrollo del proceso de enseñanza - aprendizaje de la asignatura Matemática III. Los criterios de los profesores permitirán enriquecer las acciones de la estrategia elaborada.
Acción 2.2: Actualizar anualmente la organización metodológica de la asignatura para potenciar el aprendizaje desarrollador.
Después de obtener los resultados del diagnóstico inicial de los estudiantes y conocer el estado de la preparación de los profesores mediante el desarrollo de observación a clases y encuesta, se realiza una actualización metodológica de la asignatura con vistas a garantizar el aprendizaje desarrollador de sus contenidos.
En cada clase se planifican tres momentos: introducción, desarrollo y conclusiones; con sus componentes didácticos.
Acción 2.2.1: Vinculación del contenido con el modelo del profesional.
Se realiza un análisis por el colectivo de asignatura de los objetivos definidos en el plan de estudio de la carrera, del año, la disciplina y asignatura, para valorar el papel de la Matemática III en la formación del profesional, mediante la identificación del elemento conceptual de esta asignatura que se expresa en todos ellos, el que representa el encargo social a la enseñanza de la matemática para la formación de oficiales del Minint. Posteriormente se seleccionan los contenidos que tributan de forma directa al desarrollo de las habilidades profesionales.
Acción 2.2.2: Análisis didáctico - metodológico de los contenidos.
Para el análisis del sistema de conocimientos se sugiere que los profesores analicen los núcleos conceptuales de cada uno de los temas (Ecuaciones Diferenciales, Sucesiones y Series).
Posteriormente se realiza un análisis del orden y estructuración de los contenidos por clases, para que identifiquen las rupturas respecto al orden lógico definidas en la bibliografía básica de la asignatura.
Acción 2.2.3: Análisis didáctico - metodológico de los objetivos.
Mediante el desarrollo de esta acción los profesores formulan los objetivos de cada forma organizativa, mediante el establecimiento de relaciones coherentes entre: la esencialidad del contenido, su complejidad y la habilidad para aprender, así como su orientación educativa.
Dichos objetivos deben propiciar el establecimiento de relaciones entre los conceptos, propiedades y procedimientos matemáticos conocidos y los nuevos por conocer.
Acción 2.2.4: Análisis didáctico - metodológico de los métodos y medios de enseñanza.
Los profesores seleccionarán métodos que favorezcan la participación activa y el desarrollo de las habilidades del pensamiento lógico de los estudiantes como: búsqueda parcial o heurística, investigativo, creativo, discusión, situaciones, juego de roles, simulación, exposición problémica, búsqueda parcial, enseñanza por descubrimiento o enseñanza por indagación.
Los métodos anteriores pueden ser utilizados indistintamente porque aunque tienen sus particularidades, su esencia radica en un principio común: acceder de manera independiente a los conocimientos que van a ser utilizados en la solución de problemas, y esto puede lograrse con mejores resultados si el estudiante es capaz de autorregular su aprendizaje. La utilización de estos métodos favorece el desarrollo del pensamiento lógico y de habilidades cognitivas y metacognitivas esenciales para la competencia profesional.
Acción 2.2.5: Distribución del fondo de tiempo de la asignatura por formas organizativas.
Para llevar a cabo esta acción, el colectivo de asignatura selecciona las formas organizativas a desarrollar, teniendo en cuenta aquellas que propician la participación del estudiante y el desarrollo de actividades prácticas, como elementos que propician el aprendizaje desarrollador.
Acción 2.2.6: Organización del sistema de evaluación de la asignatura.
Es importante que a la hora de evaluar se tengan en cuenta los tipos de evaluación: la autoevaluación, la coevaluación y la heteroevaluación. Dependiendo su selección, del tipo de tarea planteado por el profesor en función del objetivo trazado.
Acción 2.3: Diseñar el sistema de tareas docentes a utilizar en el proceso de enseñanza - aprendizaje de la Matemática III teniendo en cuenta los tipos de tareas propuestas.
El objetivo de esta acción es diseñar el sistema de tareas docentes, teniendo en cuenta sus diferentes tipos.
Para diseñar el sistema de tareas docentes, es importante que el profesor seleccione los tipos de tareas a utilizar, por jerarquía. Es importante que el mismo tenga presente a la hora de diseñar las tareas que debe realizarlo de forma sistémica, con una estrecha interrelación entre cada una de ellas de forma tal que el estudiante pueda ir pasando de un nivel reproductivo a uno productivo para finalmente arribar al nivel creativo, logrando así que el aprendizaje sea significativo. Además, puede apoyarse en las bondades de las TIC como los entornos virtuales de aprendizaje, y dentro de estos sus recursos para la orientación, revisión y control del estudio independiente.
Acción 2.4: Seleccionar los componentes tecnológicos a utilizar para apoyar la realización de los tipos de tareas docentes diseñadas.
Se seleccionan los componentes del entorno virtual de aprendizaje (recursos: tarea, foro, chat, wiki) a utilizar para el desarrollo de las tareas docentes propuestas por el profesor, teniendo en cuenta las potencialidades que brindan, sus facilidades de uso y los conocimientos informáticos que poseen los estudiantes, a los que va dirigida la estrategia, para el trabajo con los mismos.
Etapa 3: Ejecución.
Objetivo: Desarrollar acciones en el proceso de enseñanza - aprendizaje de la Matemática III que estimulen el aprendizaje desarrollador.
Las direcciones definidas se materializan en las acciones siguientes:
Acción 3.1: Cumplimentar las actividades metodológicas planificadas en los diferentes niveles del trabajo metodológico y evaluación de sus resultados.
Durante el desarrollo de esta acción cada colectivo metodológico deberá llevar a cabo las actividades planificadas, las que pueden sufrir cambios en dependencia de la calidad en el desarrollo del proceso de enseñanza - aprendizaje de la asignatura. Los resultados de estas actividades deben quedar en evidencia para en caso de que sea necesario realizar un cambio a alguna actividad, pueda contarse con la documentación requerida.
De igual forma se hace necesario evaluar la marcha del proceso, para lo cual debe tenerse en cuenta los criterios de los estudiantes.
Acción 3.2: Diseñar por parte de los estudiantes materiales educativos digitales que posibiliten el aprendizaje de los contenidos desde su vinculación con el modelo del profesional.
Mediante el desarrollo de esta acción, se orientará a los estudiantes desde el comienzo de la asignatura la creación de un material educativo digital (multimedia, sitio web, aplicación Androide, video educativo, grupo de infografías).
Acción 3.3: Orientación hacia el objetivo de la clase.
Esta acción se encuentra diseñada dentro de la guía de observación a clases de la UMI. La misma se explica a continuación:
Acción 3.4: Motivar al estudiante durante el desarrollo de la clase.
Esta acción se llevará a cabo mediante la aplicación de métodos productivos. El profesor partirá de una situación vinculada a la especialidad, la cual, a través de la impartición de los contenidos, deberá darle salida desde la clase.
Su redacción puede ser en forma de interrogante, planteamiento hipotético u otra forma que el profesor considere. Debe ser lo más real posible para captar la atención del estudiante y propiciar la motivación durante toda la clase.
Acción 3.5: Orientar el estudio independiente y motivación para la próxima clase.
El estudio independiente podrá ser orientado en cualquier parte de la clase. Este debe contribuir a la sistematización de los contenidos abordados en clases y su profundización. El nivel de complejidad no debe ser menor al de las actividades y tareas de la clase, para evitar la desmotivación por su realización.
Su diseño debe estar en correspondencia con las situaciones trabajadas en clase. En el caso de la asignatura Matemática III, se recomienda contar con ejercicios prácticos de cálculo, además de otros vinculados al desarrollo del material educativo digital orientado a diseñar.
Etapa 4: Control.
Objetivo: Controlar el desarrollo del proceso de enseñanza - aprendizaje de la Matemática III para el logro del aprendizaje desarrollador.
La evaluación de la estrategia didáctica tiene un carácter continuo, sistémico e integrador, al realizarse de forma interactiva entre sus escenarios de influencia: el año, colectivo de disciplina, asignatura y el proceso de enseñanza - aprendizaje, en el que se concreta y satisface el aprendizaje de los estudiantes. Se evalúa la estrategia didáctica y el aprendizaje desarrollador alcanzado por los estudiantes. Para llevar a cabo dicho control, se proponen las acciones siguientes:
Acción 4.1: Evaluar el cumplimiento de los objetivos de la asignatura Matemática III en el colectivo de año.
Se debe realizar de forma sistemática, en las reuniones metodológicas organizadas por el colectivo. Se parte de los resultados de las evaluaciones realizadas por el profesor, las que deben estar acompañadas de un análisis valorativo del avance o retroceso de cada estudiante en cuanto al aprendizaje de la asignatura.
Acción 4.2: Evaluar el cumplimiento de los objetivos de la asignatura Matemática III en el colectivo de disciplina y asignatura.
Se presentan los resultados de las evaluaciones y los contenidos con mayor dificultad en su aprendizaje. Se reorganiza el sistema de evaluación o de los restantes componentes del proceso de enseñanza - aprendizaje a partir de los resultados. Se orienta la atención a la diversidad de cada estudiante. Se potencia la participación en eventos científicos, olimpiadas de conocimientos o concursos, a partir de los resultados propios de la asignatura.
Además, se evalúa la calidad de las actividades metodológicas desarrolladas por los profesores a partir de:
Constatar (o no) el dominio de la didáctica y metodología de la enseñanza teniendo en cuenta sus propuestas para la formulación de objetivos coherentes y funcionales, sobre los métodos y medios a implementar en cada clase, la creatividad en el diseño de actividades y tareas para estimular la motivación intrínseca y el desarrollo de las habilidades del pensamiento y la independencia cognoscitiva en el estudiante.
Descripción de los principales resultados obtenidos en el cuasi - experimento
El cuasi - experimento se realizó en la UMI Eliseo Reyes Rodríguez, “Capitán San Luis”, durante el curso escolar 2018 - 2019, con una duración de un año. Se inició con un diagnóstico dirigido a precisar el estado actual de los conocimientos básicos y del aprendizaje en los estudiantes de la muestra, cuyos resultados permitieron el control y evaluación del proceso evolutivo de la variable aprendizaje desarrollador de la matemática.
Como acciones propias para propiciar al aprendizaje desarrollador se llevaron a cabo la búsqueda de información, el planteamiento de hipótesis, arribo a conclusiones, respuesta a preguntas problémicas, determinación de lo esencial, las relaciones: causa efecto ante la orientación del nuevo contenido, la comparación, razonamiento deductivo y la generalización.
Dichas acciones conllevaron al diseño de 25 materiales educativos digitales (1 aplicación Androide, 6 videos educativos, 13 infografías y 5 multimedias); el montaje de la asignatura en el entorno virtual de aprendizaje, además del diseño de un manual de la asignatura Matemática III resultado de la investigación, lo que enriquece la base material de estudio. Dichos resultados se presentaron en las Jornadas Científicas Estudiantiles a nivel de base y nacional, al igual que en eventos fuera de la universidad.
Mediante el entorno virtual se evaluaron los estudios independientes, con lo cual los estudiantes recibieron retroalimentaciones para mejorar dichos resultados. Se creó una wiki con los principales conceptos de la asignatura y se desarrollaron 12 foro debates, los que constituyen conocimiento científico acumulado de la asignatura y una traza informática de la participación de estudiantes y profesores de forma activa en el proceso de enseñanza - aprendizaje.
Se realizaron encuentros de conocimientos entre los grupos de estudio, salones tecnológicos, con la exposición de los materiales educativos digitales desarrollados desde las clases, además de encuentros con el entorno de la universidad, donde los estudiantes graficaban mediante los recursos brindados por la naturaleza, los principales conceptos y propiedades de la matemática.
Todo ello permitió que el estudiante se sintiera partícipe fundamental del proceso de enseñanza - aprendizaje e hiciera evidente su motivación y los deseos de aprender, los que participaron voluntaria y activamente; realizaron preguntas y plantearon dudas, intercambiaron continuamente sus criterios y conclusiones, las que el profesor evalúo de forma sistemática, de acuerdo a los indicadores establecidos.
Para comparar las diferencias entre el estado inicial y final del aprendizaje después de la implementación de la estrategia, se aplicó a los estudiantes de la muestra una prueba diagnóstica final y una encuesta al culminar todo el proceso, con el fin de valorar el grado de satisfacción que experimentaron con los métodos y procedimientos docentes que se implementaron y los logros alcanzados en el aprendizaje de la Matemática III.
A partir de una hipótesis alternativa bilateral y suponiendo que (= 0.05, se obtuvo como resultado p=0,000042, valor que es menor que 0,5. La mediana de la PDF es significativamente mayor que la PDI en un 95,0%. Estos resultados demuestran desde lo cuantitativo la efectividad y pertinencia de la aplicación de la estrategia didáctica para contribuir al aprendizaje desarrollador de la Matemática III en la carrera Ingeniería Informática, constituyendo una vía de solución a la contradicción fundamental declarada en la introducción de la tesis.
Conclusiones
La elaboración de una estrategia didáctica para el aprendizaje desarrollador de la Matemática III en los estudiantes de la carrera Ingeniería Informática (Perfil Informática Operativa) permitió determinar características y regularidades que distinguen el aprendizaje desarrollador de la matemática, así como con las vías para su instrumentación en la práctica.
Con la aplicación de la estrategia propuesta se lograron avances cuantitativos y cualitativos en el aprendizaje desarrollador de la Matemática III, lo que se constató al comparar los resultados del estado inicial con el final del aprendizaje, lo que confirma la factibilidad, efectividad y cumplimiento del objetivo de la investigación.
Existió consenso entre las repuestas positivas recogidas mediante el criterio de expertos, lo que demuestra que es objetiva y confiable la aplicación de la estrategia didáctica en la práctica.














