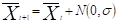Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
El vertiginoso incremento de la demanda de electricidad, las limitaciones ambientales y el escenario competitivo del mercado energético, ha provocado que los sistemas de transmisión y distribución frecuentemente operen con grandes cargas. Las experiencias recientes de fallas indican que, en muchos casos, los eventos que causan fallas generalizadas tienen lugar en los sistemas de distribución por lo que la evaluación de la confiabilidad ha ganado mucha importancia en la planificación y operación de los sistemas de distribución eléctrica. Su desarrollo demanda actualmente tecnologías inteligentes para su mejor funcionamiento.
La optimización de la reconfiguración de redes ha ganado mucho interés en los investigadores para controlar los sistemas de distribución eléctrica y mejorar su confiabilidad. La confiabilidad se considera un criterio esencial para mantener y ampliar la infraestructura de los sistemas de distribución eléctrica y los diseños basados en ella, tienen como objetivo minimizar la duración y la frecuencia de las interrupciones, lo que permite a las empresas de distribución de energía ahorrar gastos en mantenimiento y operación, especialmente después de fallas.
La reconfiguración de redes es la variación de la configuración de las redes de distribución cambiando el estado de los interruptores seccionalizadores, normalmente cerrados y de los de enlace normalmente abiertos para lograr la satisfacción de las restricciones de operación. Es un problema de optimización modelado como altamente combinatorio, porque la configuración candidata crece exponencialmente con el número de interruptores, no lineal, no diferenciable y restringido y su función puede ser de un objetivo o multiobjetivo (Beenish, et al., 2016).
Durante las últimas dos décadas se han empleado numerosos métodos para la optimización de la reconfiguración de redes, sin embargo, no existe un criterio de aceptación único de cuál es el método más apropiado. Lo más importante resulta cómo utilizar el conocimiento específico del problema y cómo modelarlo e implementarlo (Tomoiagă, et al., 2013).
La optimización de la reconfiguración de redes de distribución eléctrica hoy en día tiene que ver con el objetivo de una solución "óptima". Por lo tanto, han surgido varios métodos, que se están investigando y aplicando ampliamente. Para problemas de pequeña escala, los métodos de solución exacta, como la programación lineal, se pueden utilizar de forma eficaz. Sin embargo, cuando los problemas resultan grandes y complejos, suelen emplearse los métodos heurísticos debido al crecimiento exponencial del espacio de búsqueda y al tiempo empleado para encontrar una solución óptima o casi óptima. En las últimas décadas, los investigadores han propuesto muchos métodos heurísticos novedosos inspirados en la naturaleza (evolución natural en poblaciones biológicas), como los algoritmos evolutivos (AE), para el diseño de optimización basado en conocimientos de dominio específicos (Chiong & Beng, 2007).
Los algoritmos evolutivos (AE) son métodos heurísticos aproximados, diseñados para resolver problemas de optimización combinatoria (metaheurísticas) basadas en poblaciones. Los diseños de los métodos recientes incluyen una amplia mezcla de influencias, aunque mantienen en común la inspiración en poblaciones biológicas.
El término Algoritmo Evolutivo (AE) en ocasiones se extiende igualmente a algoritmos motivados por aspectos poblacionales que no provienen directamente de los AE tradicionales, como la búsqueda de dispersión. La computación evolutiva también se utiliza como término para referirse a los AE, pero generalmente como un término genérico que incluye algoritmos de optimización inspirados en otros procesos naturales, como la optimización del enjambre de partículas y los sistemas inmunes artificiales.
Los Algoritmos Evolutivos (AE) se fundamentan en el principio de supervivencia del más apto (es decir, evolución) y están inspirados en el concepto evolutivo darwiniano de que el sistema cambia gradualmente con el tiempo. Su funcionamiento se basa en algunos principios básicos como: Presencia de una o más poblaciones de individuos que compiten por recursos limitados. La población cambia dinámicamente y siempre buscará el espacio de posibles formas (aptitud del ajuste) para el individuo que mejor se adapte. En la naturaleza, los individuos necesitan adaptarse a su entorno para poder sobrevivir, este proceso se conoce como evolución.
En la reproducción, se crea aleatoriamente un conjunto de soluciones candidatas (elementos del dominio función) para maximizar la función de calidad que luego, en forma de función de aptitud abstracta se aplica al dominio del problema. En ella se conservan las características que hacen al individuo más apto para competir y se eliminan los elementos más débiles. Los genes son las unidades que controlan estas características, el conjunto de tales genes forma los cromosomas. Para la próxima generación, aplicando las técnicas de recombinación (representada por el operador binario que se puede aplicar a dos o más candidatos seleccionados conocidos como padres generando como resultado uno o más candidatos nuevos (hijos)) y/o mutación (que se aplica a un solo candidato y da como resultado un nuevo hijo.) se seleccionan por aptitud, algunos de los mejores candidatos. Solo los individuos más aptos sobreviven en las generaciones siguientes y sus genes más aptos se transmiten a sus descendientes durante el proceso de recombinación (crossover en inglés). Después de ejecutarse la recombinación o mutación, se genera un conjunto de nuevos candidatos basado en sus aptitudes. Este es un proceso iterativo que puede continuarse hasta que se encuentre un candidato de calidad suficientemente buena (DeJong, 2006).
Durante años, los algoritmos evolutivos han constituido un tema de estudio extremadamente atractivo y diverso, y la gran cantidad de publicaciones sobre el tema puede originar desafíos para los investigadores nuevos en el tema.
Por otra parte, en la mayoría de las investigaciones realizadas en los últimos años, se han utilizado la Inteligencia Artificial y las técnicas de búsqueda heurística para mejorar la optimización de la reconfiguración de redes de distribución eléctrica.
Teng & Liu (2003), enumeran muchos métodos y algoritmos para resolver el problema de optimización de la reconfiguración de redes de distribución eléctrica, algunos de ellos convencionales y basados en Inteligencia Artificial y técnicas de búsqueda heurística. Algunos autores han trabajado con estos métodos por separado y otros han utilizado una combinación de ellos. Sin embargo, todas las técnicas y algoritmos no consideran la incertidumbre de algunas fuentes de generación como las Fuentes Renovables de Energía (FRE). La naturaleza intermitente de tales fuentes causa problemas de confiabilidad y puede cambiar los resultados negativamente con respecto a las pérdidas de energía. Por lo tanto, todavía existe una brecha de conocimiento y una inmensa necesidad de desarrollar nuevos métodos que consideren la penetración de las redes de distribución eléctrica con fuentes de incertidumbre.
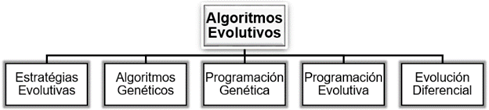
Entre los algoritmos evolutivos utilizados en muchas aplicaciones industriales entre las que se incluye la optimización de la reconfiguración de redes de distribución eléctrica se encuentran los algoritmos genéticos (AG), la programación genética (PG), la evolución diferencial (ED), la estrategia de evolución (EE) y la programación evolutiva (PE). Cada una de ellos tienen muchas variedades diferentes (Slowik & Kwasnicka, 2020).
El objetivo del artículo es realizar una exploración científica de los algoritmos evolutivos utilizados para resolver problemas de optimización entre los que se incluyen la reconfiguración óptima de redes de distribución eléctrica.
Materiales y métodos
Los algoritmos de optimización de la reconfiguración de redes de distribución eléctricas pueden clasificarse por los métodos de solución empleados: Los que se basan en una combinación de métodos heurísticos y de optimización, los que utilizan solamente heurísticas y los que utilizan algunos métodos de inteligencia artificial (IA). Numerosos investigadores defienden el uso de una combinación de técnicas heurísticas y de optimización. Esta combinación permite que la solución tenga cierto grado de precisión y asegure la convergencia con un tiempo de solución aceptable (Abdelaziz, et al., 2009).
La complejidad de las aplicaciones en problemas reales ha aumentado considerablemente. Los problemas como la optimización de la reconfiguración de redes de distribución eléctricas son muy complejos y difíciles de resolver. La Computación Evolutiva (CE), inspirada en la evolución natural darwiniana constituye un enfoque para abordar la solución de tales problemas. La computación evolutiva involucra varios algoritmos, comúnmente conocidos como Algoritmos Evolutivos (AE).
Los AE forman parte de los métodos de optimización heurísticos (del término griego εὑρίσκειν que significa: hallar, inventar). Estas metodologías de búsqueda de soluciones están fuertemente basadas en el sentido común, en el conocimiento específico del problema a resolver o incluso la imitación del comportamiento de poblaciones en el mundo animal. Los algoritmos heurísticos no pretenden encontrar la mejor solución de un problema, pero si llegar a una solución lo suficientemente buena y cercana a la solución óptima. Su desempeño es potenciado por el conocimiento del problema a resolver el cual ayuda a sintonizar el algoritmo de solución con la finalidad de acelerar su convergencia desarrollando al mismo tiempo la capacidad de explorar el espacio de soluciones de un problema particular.
Los AE tienen la característica común de operar sobre una búsqueda iterativa de soluciones. Se espera que el resultado de cada iteración mejore en relación al resultado de la iteración anterior. Es común llamar “generación” al resultado de cualquier iteración. La búsqueda de la mejor solución trae implícita la necesidad de evaluar la fortaleza o robustez de cada una de ellas para luego preservarla o desecharla en beneficio de cualquier solución existente o venidera. La robustez de las soluciones que produzca el algoritmo determinará la robustez del algoritmo en sí mismo. Sin perder de vista que el propósito principal es encontrar las soluciones que maximicen o minimicen la función objetivo, la robustez de cada solución será evaluada si contribuye a maximizar o minimizar dicha función.
La premisa de los Algoritmos Evolutivos es bastante simple dado que está familiarizado con el proceso de selección natural. Los AE contienen cuatro pasos fundamentales: inicialización, selección, operadores genéticos y terminación. Cada uno de estos pasos corresponde, aproximadamente, a una faceta particular de la selección natural y proporciona formas fáciles de modularizar sus implementaciones. Resumiendo, en un AE los miembros más aptos sobrevivirán y proliferarán, mientras que los no aptos morirán y no contribuirán al acervo genético de generaciones futuras, de manera similar que en la selección natural.
Los algoritmos evolutivos (AE) surgieron como un método importante de optimización y búsqueda, en la última década. Son un subconjunto de las Computaciones Evolutivas (CE) y pertenecen al conjunto de métodos de búsqueda estocásticos generales basados en la heurística moderna. Debido a sus naturalezas flexibles y al comportamiento robusto heredado de la Computación Evolutiva, constituyen métodos ampliamente utilizados y eficientes, para la solución de problemas de optimización global. Pueden utilizarse exitosamente, en muchas aplicaciones de alta complejidad (Vikhar, 2016). En los últimos años, se han convertido en una herramienta muy popular para buscar, optimizar y proporcionar soluciones a problemas complejos.
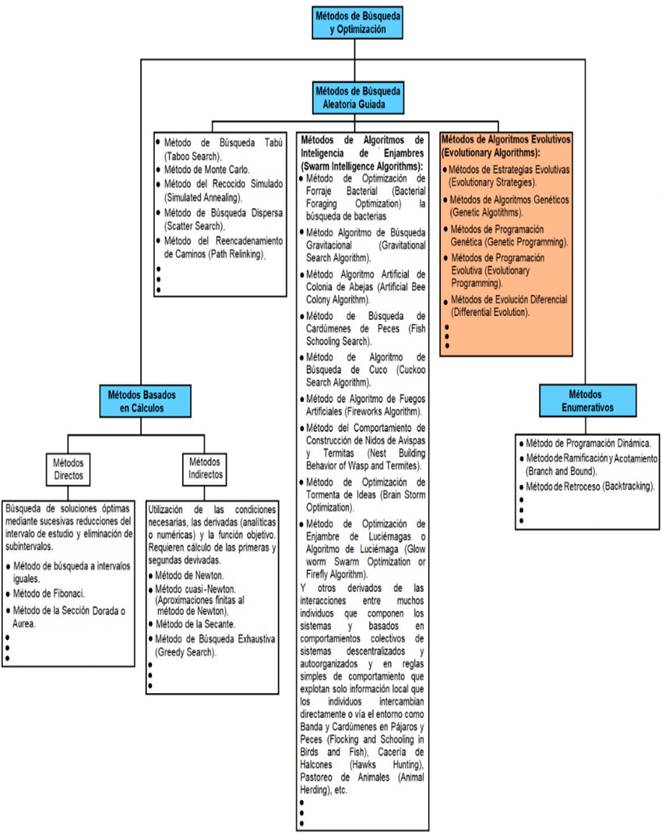
La figura 1 muestra la ubicación de los Algoritmos Evolutivos (AE) dentro de los métodos de búsqueda y optimización y su clasificación principal en el dominio de la Computación Evolutiva (CE).
Por otra parte, en las últimas dos décadas además de los Algoritmos Evolutivos se han empleado numerosos otros métodos en la optimización de la reconfiguración de redes de distribución eléctrica. No obstante, no existe una aceptación absoluta de cuál es el método más apropiado en los problemas de optimización de la reconfiguración de redes. Lo más importante radica en cómo utilizar el conocimiento específico del problema a resolver y cómo modelarlo e implementarlo (Tomoiagă, et al., 2013).
Debido a la existencia de muchos métodos heurísticos de naturaleza muy diferente y diversa, y considerando que generalmente estos se diseñan para problemas específicos, sin posibilidad de generalización o aplicación a otros problemas similares, resulta extremadamente complicado hacer una clasificación completa de los mismos por lo que suele plantearse un conjunto de categorías no excluyentes en la que se pudieran ubicar los principales métodos desarrollados.
Considerando lo anterior, en la Figura 2 se muestra la ubicación de los Algoritmos Evolutivos (AE) en los métodos utilizados en la optimización de la reconfiguración de redes de distribución.
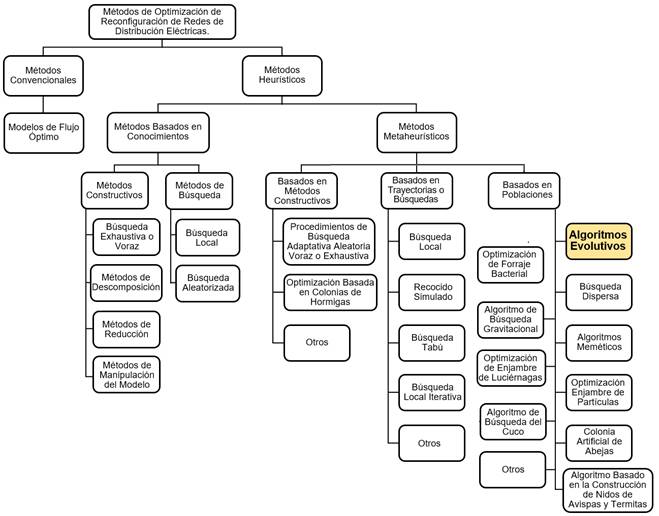
Fig. 2 - Propuesta de ubicación de los Algoritmos Evolutivos (AE) en los métodos de optimización de la reconfiguración de redes de distribución eléctricas.
Clasificación de los Algoritmos Evolutivos
Existen numerosas variantes de Algoritmos Evolutivos y además variantes hibridas, que igualmente incorporan algunas técnicas de ellos. Sin embargo, la estructura de cualquier método evolutivo es muy similar. Todos los Algoritmos Evolutivos tienen en común la evolución simulada de individuos y se diferencian por sus modos de implementación y por las formas de aplicación a problemas específicos. Se inspiran en procesos de la evolución biológica, como la reproducción, la mutación, la recombinación y la selección. Se crea aleatoriamente un conjunto de soluciones candidatas (es decir, elementos del dominio de función) para maximizar la función de calidad. Luego, se aplica la función de calidad al dominio del problema en forma de función de aptitud abstracta. Para la próxima generación, se seleccionan algunos mejores candidatos basados en la función de aptitud. Esto se logra aplicándoles la técnica de recombinación y/o mutación. La recombinación está representada por el operador binario. Este operador se puede aplicar a dos o más candidatos seleccionados conocidos como padres y genera uno o más candidatos nuevos (hijos) como resultado. Mientras que la mutación se aplica a un solo candidato y da como resultado un nuevo hijo. Después de ejecutar la recombinación o mutación, se genera un conjunto de nuevos candidatos en función de sus aptitudes. Este es un proceso iterativo. Puede continuarse hasta que se encuentre un candidato de calidad suficientemente buena.
Actualmente, toda la familia de optimización evolutiva se cita como algoritmos de Computación Evolutiva (CE). La figura 3 representa la clasificación de los Algoritmos Evolutivos bien conocidos y comúnmente utilizados que, en este dominio, consecuentemente pueden mencionarse como más populares y principales: Estrategias Evolutivas (EE), Algoritmos Genéticos (AG), Programación Genética (PG), Programación Evolutiva (PE) y Evolución Diferencial (ED).
Generalidades sobre los Algoritmos Evolutivos (AE) más populares
Estrategias Evolutivas (EE)
Las Estrategias Evolutivas son una familia de algoritmos estocásticos de optimización numérica de funciones no-lineales o problemas de optimización continua no convexa donde no es posible conocer a priori la forma del espacio de soluciones ni es factible realizar el cálculo de las derivadas sucesivas. Fueron introducidas por Rechenberg a principio de los años 70 en diferentes aplicaciones industriales e hidráulicas. Se destacan porque trabajan en espacios continuos (números reales) y porque los parámetros de funcionamiento del algoritmo (tasa de mutación, probabilidad de cruce.) no son fijos, sino que forman parte del proceso de optimización.
Las Estrategias Evolutivas son la categorización de los modelos de cada uno de los algoritmos evolutivos. Por su naturaleza son técnicas de búsqueda y optimización metaheurísticas que operan con un criterio de búsqueda más amplio al utilizar elementos de selección y mutación. Existen métodos de selección simples o altamente desarrollados para escoger los individuos que producirán la siguiente generación de soluciones. Por otra parte, utilizan el cruzamiento o recombinación de las características esenciales de los individuos de cada población para producir la descendencia perteneciente en la siguiente generación. La robustez de cada individuo en determinada generación es evaluada a lo largo de las iteraciones con el propósito de modular la búsqueda de soluciones siguientes y acelerar los procesos de convergencia.
Las EE están básicamente enfocadas hacia la optimización paramétrica. En esencia son métodos estocásticos con paso adaptativo, que permiten resolver problemas de optimización paramétrica. Pueden definirse como algoritmos evolutivos enfocados hacia la optimización paramétrica, teniendo como características principales que utilizan una representación a través de vectores reales, una selección determinística y operadores genéticos específicos de cruce y mutación. Además, su objetivo fundamental consiste en encontrar el valor real de un vector de N dimensiones. Pueden dividirse en dos tipos: Estrategias Evolutivas Simples y Estrategias Evolutivas Múltiples.Las Estrategias Evolutivas Simples se consideran procedimientos estocásticos de optimización paramétrica con paso adaptativo, esta característica las hace similares al recocido simulado. En este caso, se hace evolucionar un solo individuo usando únicamente a la mutación como operador genético. Las Estrategias Evolutivas Múltiples surgen como respuesta a las debilidades de las Estrategias Evolutivas Simples, las cuales tienden a converger hacia subóptimos. En ellas existen múltiples individuos (población), y se producen en cada generación varios nuevos individuos, usando tanto mutación como cruce (también puede usarse cualquier otro operador).
Algunos tipos de sus procedimientos son (García, 2014; Peñaherrera, 2015):
(1 + 1) -ES o estrategia evolutiva de dos miembros, que utiliza solamente un padre y un descendiente. Opera donde cada padre produce solo una mutación (hijo) que compite con él. El mutante se convertirá en el padre de la próxima generación solo si se desempeña mejor que el padre original. Si no es así, se omite el mutante. En la siguiente generación el siguiente hijo es calculado a partir de valores normales por la ecuación 1
(1)
donde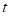 
se refiere a la generación actual y N es un vector de números Gaussianos con media 0 y desviación estándar 
.
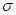(μ + 1) -ES, primera generalización de la estrategia anterior (1+1). En este caso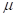 
padres son usados para cada generación. A su vez cada padre es asociado con un vector σ el cual controla la magnitud de las mutaciones. Los padres se combinan entre ellos para formar un único hijo o descendencia, y entonces el hijo es mutado produciendo la siguiente generación. Los padres de la siguiente generación se escogen entonces entre los 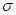mejores individuos los cuales son escogidos de entre los padres de la generación anterior y los hijos mutados de la generación recientemente obtenida.
(1 + λ) -ES, en el que se generan mutantes λ y se selecciona el mejor mutante como el nuevo padre en la siguiente generación, mientras que el padre actual se omite sin considerar su idoneidad.
(μ + λ) -ES, en la que el tamaño de la población lo define la cantidad μ padres, los cuales en cada generación producen λ hijos. En este punto tendremos (μ + λ) individuos los cuales incluyen tanto a padres como a hijos. Se seleccionarán entonces los mejores μ individuos como los padres de la siguiente generación.
(μ, λ) -ES, en que los padres de la siguiente generación son seleccionados de entre los mejores μ individuos de los λ hijos. Es decir, ninguno de los padres de la generación anterior sobrevive, y solo un subconjunto de los hijos es elegido como la siguiente generación de padres. Para asegurar esta estrategia se debe cumplir siempre que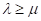 
. Ninguno de los padres de la generación anterior sobrevive a la siguiente generación y la vida de cada individuo está restringida a la de su propia generación.
(μ / ρ +, λ) -ES, que es bastante contemporánea y se utiliza frecuentemente como ES estándar. 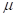: representa el número de individuos contenidos en la población parental y 
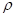: el número decidido de individuos parentales utilizados para la recombinación. Por tanto, ρ debe ser igual o menor que 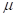. λ: es el número de hijos producidos en cada generación. Debe tenerse en consideración que todos estos parámetros son números enteros positivos. +, es el operador que decide la estrategia que se aplica, si es una estrategia de "más" o de "coma". La estrategia "más"(+) ignora la edad de los individuos, lo que significa que los padres compiten con sus hijos para sobrevivir y ser comprados en la próxima generación. La estrategia de "coma" (,) es la que los padres siempre se omiten y los nuevos padres se eligen del descendiente (hijo) más apto para la nueva generación (Hansen, et al., 2015).
(μ, k, λ, ρ) -ES, en la que se asume que dos padres se recombinan para formar un hijo, sin embargo, no existe ninguna restricción matemática para que puedan ser más de dos los padres que puedan recombinarse. Se designa con la letra ρ el número de padres que contribuyen a la generación de un hijo. Adicionalmente, si se limita la vida de cada individuo a una generación se utiliza el parámetro k, en este caso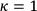 
. Si no se limita la vida de cualesquiera de los individuos y este podría sobrevivir de generación en generación en función de su robustez, se dice que 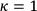. La selección adecuada de esta condición depende del tipo y naturaleza del problema tratado.
Algoritmos Genéticos (AG)
Los Algoritmos Genéticos (AG) son algoritmos de optimización de búsqueda que intentan resolver problemas complejos empleando el concepto de la evolución y basados en el proceso genético de los organismos vivos y en los principios de selección natural y supervivencia de los más fuertes (postulados de la teoría de la evolución de Darwin (1859)). Utilizan una analogía directa con el comportamiento natural, de acuerdo al cual, los individuos más aptos de una población se adaptan más fácilmente a los cambios que se producen en su entorno y sobreviven, con un enfoque fundamentado en la población en la que sus miembros se clasifican en función de la idoneidad de sus soluciones.
El libro “Adaptación en Sistemas Naturales y Artificiales. Un Análisis Introductorio con Aplicaciones a la Biología, el Control y la Inteligencia Artificial” de John Holland, 1975 se considera por muchos autores el trabajo que inspiró el desarrollo de este tema. Los AG forman una nueva población (se puede representar en un conjunto de cadenas (denominadas cromosomas)) utilizando operadores genéticos específicos como el cruce, la reproducción y la mutación. En cada generación, se crea un nuevo cromosoma (un miembro de la población) utilizando información procedente de los cromosomas más aptos de la población anterior.
Los Algoritmos Genéticos generan una población inicial de soluciones factibles y las combinan de manera que oriente su búsqueda hacia áreas con más posibilidades en el espacio de búsqueda. Ejecutan una búsqueda simultánea en diferentes regiones del espacio factible, realizan una intensificación sobre algunas de ellas y exploran otros subespacios a través de un intercambio de información entre configuraciones. Cada una de estas soluciones factibles está codificada como un cromosoma, también conocido como genotipo, y cada uno de estos cromosomas obtendrá una medida de aptitud (fitness) a través de una función de aptitud (función objetivo o de evaluación). El valor de la función de aptitud de un cromosoma determina su capacidad para soportar y producir descendencia. El alto valor de aptitud indica la mejor solución para la maximización y el bajo valor de aptitud indica la mejor solución para los problemas de minimización.
Los Algoritmos Genéticos tienen cinco componentes principales: Generador de números aleatorios, unidad de evaluación de la aptitud, proceso de reproducción, proceso de cruzamiento y operación de mutación. La reproducción selecciona a los candidatos más aptos de la población, mientras que el cruce es el procedimiento de combinar los cromosomas más aptos y pasar genes superiores a la siguiente generación, y la mutación altera algunos de los genes de un cromosoma. En uno de los enfoques más comunes utilizados en los Algoritmos Genéticos, la operación comienza con la determinación de una población inicial, al azar o mediante el uso de algunas heurísticas. La selección es el operador genético que permite elegir las configuraciones de la población actual que deben participar de la generación de las configuraciones de la nueva población (nueva generación). Este operador termina después de decidir el número de descendientes que debe tener cada configuración de la población actual (Hincapié, et al., 2004). La función de aptitud se utiliza para evaluar a los miembros de la población y luego se clasifican en función de las actuaciones. Una vez que se han evaluado todos los miembros de la población, se omiten los cromosomas de rango inferior y las poblaciones restantes se utilizan para la reproducción (Ab Wahab, et al., 2015). Otros esquemas permiten la selección de cromosomas de rango inferior para la reproducción (pseudoaleatorios).
En el proceso de cruzamiento se seleccionan aleatoriamente dos miembros de la población restante (los cromosomas más aptos) y se intercambian y emparejan. Permite pasar información genética de un par de cromosomas originales a sus descendientes, o sea, saltar de un espacio de búsqueda a otro, generando de esta forma diversidad genética. En el paso final mutación, el operador muta aleatoriamente en un gen de un cromosoma, que permite realizar la intensificación en un espacio en particular caminando a través de vecinos. La mutación significa intercambiar el valor de un gen de un cromosoma en una población. En forma aleatoria, se elige un cromosoma como candidato, se genera un número aleatorio y si es menor que la tasa de mutación (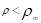
), entonces se realiza la mutación (Hincapié, et al., 2004). La tasa de mutación se elige del rango [0.001, 0.05]. La mutación asegura que se pueda llegar a todas las regiones del espacio del problema, por lo que constituye un proceso esencial. El elitismo se utiliza para evitar que la mejor solución de la población sea destruida durante las operaciones cruzamiento y mutación. Garantiza además que la aptitud de la nueva generación sea al menos tan buena como la generación actual. La evaluación y generación de las nuevas poblaciones se continúa hasta que se alcanza el número máximo de generaciones o se encuentra la solución óptima.
Si los Algoritmos Genéticos son bien diseñados, la población convergerá a una solución óptima del problema. Constituyen una técnica robusta y pueden resolver con éxito gran variedad de problemas provenientes de áreas muy diferentes incluso aquellos en que otros métodos encuentran dificultades (Moujahid, et al., 2008).
Los Algoritmos Genéticos tienen como ventajas que no necesitan conocimientos específicos sobre el problema que intentan resolver, operan de forma simultánea con varias soluciones, en vez de trabajar de forma secuencial como las técnicas tradicionales, resultan menos afectados por los máximos locales (falsas soluciones) que las técnicas tradicionales, en problemas de optimización que maximizan la función objetivo, requieren ajustes limitados de parámetros y que se inicializan así mismos a partir de soluciones y no de una solución única y utilizan operadores probabilísticos, en lugar de los típicos operadores determinísticos de las otras técnicas. Tienen las desventajas que pueden tardar en converger hacia los valores óptimos o no converger, como resultado de que los procesos de cruzamiento y mutación son aleatorios o pueden también converger prematuramente (Ab Wahab, et al., 2015).
Programación Genética (PG)
La Programación Genética es un paradigma de computación evolutiva para encontrar programas de computación que realicen una tarea definida por el usuario. Se trata de una especialización de los algoritmos genéticos donde cada individuo es un programa. En ella, las soluciones están en forma de programas y sus aptitudes las determina su capacidad de resolver problemas computacionales. Por tanto, puede considerarse una técnica de aprendizaje automático usada para optimizar una población de programas de computación según una heurística definida en función de la capacidad del programa para realizar una determinada tarea computacional, definida por el usuario.
La PG desarrolla programas informáticos, tradicionalmente representados en la memoria como estructuras de árboles. Los árboles pueden ser fácilmente evaluados de forma recursiva. Cada nodo del árbol tiene una función como operador y cada nodo terminal tiene un operando, por lo que las expresiones matemáticas son fáciles de evolucionar y evaluar. Así, tradicionalmente la PG favorece el uso de lenguaje de programación que, naturalmente, introduce las estructuras de árbol. Se usa principalmente para optimizar programas de computadora o expresiones matemáticas, pero se puede usar para cualquier problema que requiera soluciones estructuradas en árbol. Un uso común es la regresión simbólica, que implica encontrar una expresión matemática que se ajuste a un conjunto de datos en particular.
Los principales operadores usados en la Programación Genética son: cruzamiento y mutación. El cruzamiento es aplicado a un individuo mediante simples intercambios entre uno de sus nodos por otro nodo de otro individuo de la población. Con una representación basada en árboles, la sustitución de un nodo implica la sustitución de toda la rama. Esto añade una mayor efectividad al operador de cruce. Las expresiones resultantes del cruce son muy diferentes de sus padres iniciales.
La mutación afecta a un individuo de la población. Se puede sustituir un nodo entero en el individuo seleccionado, o puede simplemente reemplazar la información del nodo. Para mantener la integridad, las operaciones deben sersalvo falloso el tipo de información que el nodo tiene debe ser tomada en cuenta.
La programación genética (PG) es una forma especializada de Algoritmos Genéticos que opera sobre tipos de solución muy específicos, utilizando operadores genéticos modificados. Fue desarrollada por Koza como un intento de encontrar el camino para la generación automática de los códigos de programa cuando se conocen los criterios de evaluación para su correcto funcionamiento. Debido a que la solución buscada es un programa, las soluciones potenciales evolucionadas se codifican en forma de árboles en lugar de cromosomas lineales (de bits o números) generalizados en los Algoritmos Genéticos (Slowik & Kwasnicka, 2020).
Se aplica a la ingeniería de software a través de la síntesis de código, la mejora genética, la corrección automática de errores y el desarrollo de estrategias de juego, etc. Los tipos de Programación Genética incluyen: Programación genética basada en árboles, Programación genética basada en pilas o cúmulos, Programación genética lineal (PGL), Evolución gramatical, Programación genética compacta ampliada (PGCA), Programación genética cartesiana (PGC), Evolución probabilística incremental del programa (EPIP), Programación genética fuertemente tipificada (PGFT), Mejora genética de software para múltiples objetivos (MGSMO).
Programación Evolutiva (PE)
La programación evolutiva (PE) es una rama de la Computación Evolutiva y uno de los cuatro paradigmas principales de los Algoritmos Evolutivos. Es similar a la Programación Genética (PG), pero la estructura del programa a optimizar es fija, mientras que sus parámetros numéricos pueden evolucionar. Fue utilizado por primera vez por Lawrence J. Fogel en los EE. UU, en los años 60. La programación evolutiva es prácticamente una variación de los algoritmos genéticos, donde lo que cambia es la representación de los individuos. En el caso de la PE los individuos son ternas (tripletas) cuyos valores representan estados de un autómata finito. Cada terna está formada por: El valor del estado actual, un símbolo del alfabeto utilizado y el valor del nuevo estado. Estos valores se utilizan, como en un autómata finito, de la siguiente manera: Teniendo el valor del estado, se toma el valor del símbolo actual y si es el símbolo de la terna que se tiene, debe moverse al nuevo estado.
En la optimización de la programación evolutiva estándar, el aprendizaje se implementa normalmente, como los algoritmos de búsqueda local. Estos métodos prueban iterativamente varias alternativas en el entorno de aprendizaje individual intentando encontrar mejores soluciones. Al final del proceso de aprendizaje la calidad de un individuo será no solo el valor de su formación inicial sino también el de su habilidad para mejorar.
El énfasis en este paradigma está en la evolución del comportamiento más que en el genotipo. Debido a que el genotipo no ha evolucionado, no se usa ningún método de cruce entre padres, solo mutación. Los individuos se crean solo mutando a los padres, donde la cantidad de mutación se conoce como comportamiento. Además, no se utiliza ninguna función de aptitud bruta, sino que se favorece la aptitud relativa. El valor de aptitud relativa se utiliza en lugar del valor bruto de aptitud para medir cuánto mejor se desempeñan los individuos en relación con los que los rodean.
La Programación Evolutiva se centra en la evolución del comportamiento de los individuos y no del genotipo, la mutación es el único operador de reproducción utilizado, sin cruzamientos. El operador de mutación debe poder introducir nuevo material genético de manera suficientemente eficiente para adaptarse a la falta de intercambio genético entre individuos que se produce en los cruzamientos. Los tipos principales de operadores de mutación son: No adaptativo (estático), dinámico y autoadaptativo. En los estáticos, el dominio de la mutación permanece constante o estático, en los dinámicos, se disminuye lentamente la mutación máxima unida con cada generación para fomentar la exploración en las primeras generaciones y la explotación en las últimas y en los autoadaptativos, la mutación no es estática o dinámica, pero tiene la capacidad de aumentar, disminuir o permanecer igual en un momento dado, en dependencia de la aptitud relativa del entorno (Morgan, 2021).
Evolución Diferencial (ED)
La Evolución Diferencial (ED) se caracteriza por el uso de vectores de prueba, que compiten para sobrevivir, con los individuos de la población actual. Se basa en diferencias de vectores y por lo tanto es apropiada principalmente para problemas de optimización numéricos.
Es un método que optimiza un problema intentando mejorar iterativamente una solución candidata con respecto a una determinada medida de calidad (metaheurística poblacional) que realiza pocas o ninguna suposición en el problema que se está optimizando y puede buscar en espacios muy grandes de soluciones candidatas. Fue originalmente propuesta por Rainer Storn y Kenneth Price en octubre de 1995 para minimizar funciones no diferenciables y posibles continuas no lineales.
De manera formal, cada individuo 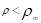de la población se define por la tupla 
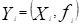. Donde 
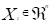es el vector solución y 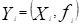el valor correspondiente de la función objetivo. Como todo algoritmo evolutivo consta de dos etapas generales: inicialización y ciclo principal. En el primero, la población es pseudo-aleatoriamente inicializada en el espacio de búsqueda, mientras que en el ciclo principal se generan nuevos individuos (soluciones candidatas) mediante cruzamiento y mutación. La aplicación de estos operadores evolutivos es controlada por el parámetro CR. El operador de reemplazamiento es simple y no depende de una generación (iteración) del algoritmo: si el nuevo individuo es mejor (más apto) entonces este reemplaza al individuo que le dio origen. En particular, la mutación depende básicamente del parámetro F conocido como factor de escala.
La Evolución Diferencial optimiza un problema manteniendo una población de soluciones candidatas y creando nuevas soluciones candidatas mediante la combinación de las existentes de acuerdo con sus fórmulas simples, para posteriormente, mantener la solución candidata que tenga la mejor puntuación o aptitud en el problema que se está optimizando. El flujo general de los algoritmos de evolución diferencial puede describirse de la siguiente forma: Después de inicializar la población, se utiliza algún tipo de procedimiento de selección, para la reproducción de múltiples padres. A partir del conjunto de padres, se realiza la mutación mediante la creación del vector unitario, que entonces se cruza con el padre "principal" para crear la descendencia final. Para la próxima generación, se seleccionan como sobrevivientes, el mejor descendiente y el padre "principal".
El operador de mutación en la Evolución Diferencial se crea a partir de dos componentes, una diferencia y un vector objetivo. El vector de diferencia es un vector de las diferencias entre dos o más padres, donde el vector objetivo es el padre cuya dirección se priorizará en la creación del vector unitario. El vector unitario es el producto final del proceso de mutación que luego se utiliza en el cruzamiento con el padre "principal" actual, (padre de interés no incluido en la mutación). Por su parte en el cruzamiento - similar a los algoritmos genéticos estándares - se cuenta con dos tipos: el promedio y el intuitivo. El cruce en la evolución diferencial es como el de los algoritmos genéticos estándar, lo que significa que tenemos dos tipos: promedio e intuitivo. Después de crear el vector unitario, se selecciona el padre "principal", diferente a los utilizados anteriormente, y luego se realiza el cruzamiento entre ese nuevo padre y el vector unitario, para la obtención de la descendencia final (Morgan, 2021).
Comparación entre los Algoritmos Evolutivos (AE) más populares
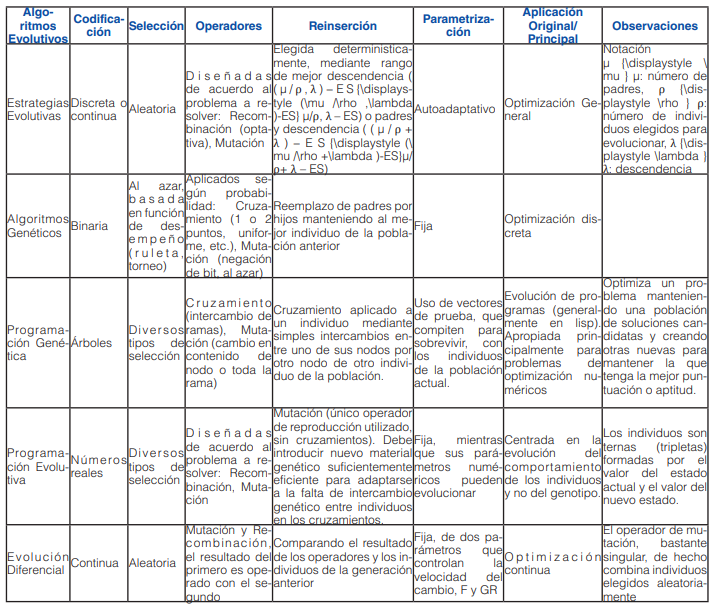
Cada uno de los algoritmos evolutivos anteriores no obstante ser en esencia evolutivos, se diferencian entre sí en ciertas características necesarias a distinguir entre ellos. La tabla 1 presenta una comparación entre los algoritmos evolutivos más populares analizados. Las características comparadas corresponden a las implementaciones originales. En la actualidad, esas entre ellos tienden a borrarse en la medida en que se transfieren características de uno a otro, haciendo difícil la distinción (García, 2014).
Ventajas y Tendencias de los Algoritmos Evolutivos
Los Algoritmos Evolutivos (AE) se han utilizado y utilizan ampliamente en muchas aplicaciones complejas de resolución de problemas, entre los que se incluye la optimización de la reconfiguración de redes de distribución eléctrica, debido a sus muchas ventajas sobre las técnicas clásicas de búsqueda y optimización. Como están inspirados en la evolución natural, son conceptualmente simples y flexibles; utilizan información previa sobre el problema que le permite ampliar el espacio de búsqueda; son independientes de la representación; cada evaluación en ellos realiza operaciones paralelas; son robustos y se desarrollan para adaptar la solución en un entorno cambiante y demuestran su capacidad de resolver problemas sin ninguna experiencia humana (Vikhar, 2016). Además de tantas ventajas, los AE sufren algunos problemas, como que no asegura siempre dar una solución óptima (pueden converger prematuramente a una solución subóptima en lugar de una óptima) a un problema específico dentro de un tiempo predecible; puede necesitar ajustes de parámetros por prueba y error (problemas con la compensación óptima entre las propiedades de exploración y explotación) y necesita muchos recursos computacionales.
Como los algoritmos evolutivos son un dominio de investigación popular, como tendencia, sistemáticamente, se proponen muchas modificaciones.
Entre las direcciones principales de las tendencias de los Algoritmos Evolutivos (AE) está la hibridación de dos o más algoritmos para obtener mejores resultados y las modificaciones que se realizan para mejorar su rendimiento computacional. Pueden mencionarse también entre sus tendencias de investigación, los algoritmos meméticos (sinergia de los algoritmos evolutivos o de cualquier otro enfoque basado en la población, con técnicas de búsqueda locales independientes). Algunos autores señalan, además, el creciente interés en aplicar los AE a sistemas incorporados o embebidos, es decir, empleando la evolución en poblaciones para las que las soluciones candidatas son controladores o impulsores que implementan la estrategia operativa para algunos entes situados y se evalúan dentro del contexto de un entorno rico y dinámico: por lo que realizan y no por lo que son.
Otro tema importante que requiere mayor esfuerzo en las futuras propuestas y que resulta crucial en la decisión de si el algoritmo es útil en aplicaciones reales, lo constituye la optimización de funciones en dominios de altas dimensiones en aplicaciones industriales, que suele ser muy compleja y requiere de mucho tiempo computacional, por lo que exigen que los AE sean diseñados para ser implementados fácilmente para ejecutarse en paralelo (o fáciles de ejecutar en Unidades de Procesamiento Gráfico (UPG)) para reducir su tiempo computacional.
La búsqueda de nuevas técnicas en áreas como el ajuste automático y el control de parámetros adaptativos continúa siendo un tema candente en los AE, pues los valores de los parámetros de los AE que son "buenos" en un problema no pueden ser suficientes en otro.
Los nuevos algoritmos evolutivos que se desarrollen en el futuro, deberán garantizar la repetitividad de los resultados generados en cada ejecución de los métodos, no obstante ser técnicas estocásticas
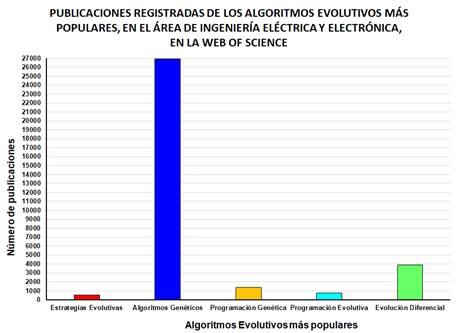
Las figuras 4 y 5, muestran las publicaciones registradas en el Google Académico y en la Web of Science, respectivamente.
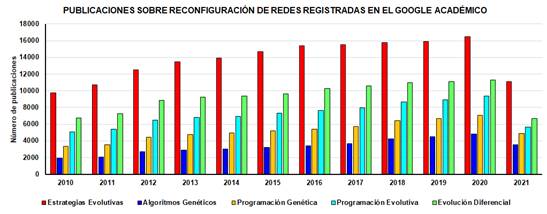
Fig. 4 - Número de publicaciones registradas sobre el empleo de Algoritmos Evolutivos en reconfiguración de redes, en Google Académico en los últimos diez años.
Fuente: Slowik & Kwasnick (2020).Fig. 5 - Número de publicaciones registradas en la Web of Science de los Algoritmos Evolutivos más populares.
Resultados y discusión
Los Algoritmos Evolutivos son una potente herramienta en optimización de formas. Debido a su relativa sencillez en comparación con otros métodos algorítmicos, su facilidad de uso, y su capacidad para adaptarse a los problemas de optimización multi-objetivo, los AE han sido aplicados a problemas de optimización de diseños en muchas áreas. La adaptabilidad y la simplicidad de las técnicas evolutivas permiten su aplicación en estos casos obteniendo muchas veces soluciones más eficientes que la optimización numérica directa y ahorrando un considerable esfuerzo computacional.
En la actualidad, en el área de la investigación en informática, puede observarse una fuerte presión en la búsqueda de nuevas técnicas de optimización basadas en la naturaleza. Por su sencillez, flexibilidad y robustez, los Algoritmos Evolutivos se han convertido en una popular técnica de solución de optimizaciones que, al contar con muchos tipos de métodos, se destacan como prometedoras áreas en la solución de una amplia gama de problemas (Slowik & Kwasnicka, 2020). Todos se basan en el principio común de la simulación de la evolución de los individuos utilizando los procesos de selección, mutación y reproducción, pero se diferencian entre sí en sus modos de implementación y en la forma en que se aplican a problemas particulares. Los más adecuados se seleccionan en función de la representación del problema. Los Algoritmos Genéticos y la Programación Evolutiva son los enfoques más populares utilizados para la representación binaria. Las Estrategias Evolutivas se utilizan para la optimización de parámetros de números reales, mientras que las funciones o los programas informáticos se optimizan mediante la Programación Genética. Por otra parte, en ocasiones se amplían a Algoritmos Meméticos y a Estrategias Evolutivas distribuidas, para aumentar el rendimiento de búsqueda y en otras, se combinan algunos de sus diferentes enfoques, que generan muchas mejoras en la solución de una variedad de aplicaciones de la vida real. En la actualidad, los AE atraen la atención notable de muchos investigadores (Vikhar, 2016).
Muchos autores utilizan de modo equivalente la terminología Algoritmos Evolutivos y Computación Evolutiva, para enfatizar el hecho que los AE son implementados en computadoras. Sin embargo, la Computación Evolutiva no necesariamente refiere al estudio de problemas de optimización. Los AE son específicamente algoritmos de optimización evolutiva, hecho que los distingue de la Computación Evolutiva. En contraposición, el uso de la terminología “optimización basada en poblaciones” como un equivalente de los AE sugiere de manera directa la naturaleza de este tipo de técnicas, las cuales usualmente se basan en una población de soluciones candidatas las cuales con el paso del tiempo evolucionan cada vez hacia poblaciones que tienen mejor respuesta como una solución del problema planteado.
La reconfiguración de redes puede definirse como un problema de optimización consistente en encontrar una configuración que maximice/minimice cierta función objetivo. Puede formularse como una optimización no lineal, con restricciones y con una función objetivo no diferenciable. Su solución es muy difícil por cuanto el número de configuraciones candidatas crece exponencialmente con el número de interruptores disponibles, generando una explosión de combinaciones y un esfuerzo computacional impracticable para lograr la mejor configuración. Además, debido que la posición de los interruptores seccionalizadores y de enlace es binaria (abiertos o cerrados), el espacio de solución es discontinuo. Entre los numerosos métodos propuestos en la literatura se encuentran los Algoritmos Evolutivos, que usualmente logran soluciones de buena calidad y cercanas a las óptimas.
Los algoritmos evolutivos con frecuencia, funcionan bien al aproximar soluciones a todo tipo de problemas porque, idealmente, no hacen ninguna suposición sobre el panorama de aptitud subyacente. Aplicados al modelado de la evolución biológica se limitan generalmente a la exploración de procesos microevolutivos y modelos de planificación basados en procesos celulares. En la mayoría de las aplicaciones reales de los AE, la complejidad computacional es un factor prohibitivo. De hecho, esta complejidad computacional se debe a la evaluación de la función de aptitud. La aproximación a la aptitud (fitness) es una de las soluciones para superar esta dificultad. Sin embargo, los AE aparentemente simples pueden resolver problemas a menudo complejos; por lo tanto, puede que no haya un vínculo directo entre la complejidad del algoritmo y la complejidad del problema.
La eficacia, medida como una mejor convergencia de cualquiera de las Estrategias Evolutivas (EE) descritas en el artículo, depende de la naturaleza del problema a resolver, y en unos casos una estrategia funciona mejor que la otra (Peñaherrera, 2015). Cualquier estrategia evolutiva se puede generalizar como 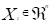, la cual tiene μ padres, cada individuo de una población puede tener una vida de k generaciones, y cada generación puede producir 
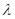hijos, cada uno de los cuales desciende de una combinación de 
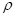padres.
Si bien no se garantiza que los Algoritmos Genéticos (AG) encuentren la solución óptima del problema, existe evidencia empírica de que se encuentran soluciones de un nivel aceptable, en un tiempo competitivo comparado con el resto de los algoritmos de optimización combinatoria. El gran campo de aplicación de los Algoritmos Genéticos se relaciona con aquellos problemas para los cuales no existen técnicas especializadas. Incluso en el caso en que dichas técnicas existan, y funcionen bien, pueden efectuarse mejoras de las mismas hibridándolas con los Algoritmos Genéticos (Moujahid, et al., 2008).
A diferencia de los enfoques matemáticos estándar para la regresión, como el ajuste de curvas, la Programación Genética (PG) hace relativamente pocas suposiciones sobre la función que generó los datos, lo que permite una amplia exploración del espacio de posibles soluciones. La PG también se usa ampliamente para resolver problemas de clasificación. De manera más general, los investigadores en PG están interesados en la programación automática, es decir, encontrar programas de computadora que resuelvan una tarea en particular, y existen muchas variantes de PG que utilizan formas particulares de representación de programas. La Programación Genética PG) también ha sido ampliamente utilizada para generar estructuras complejas, como grandes redes neuronales (Deb & Jain, 2014), donde se puede elegir una representación del genotipo que comprima características repetitivas como la simetría y la modularidad. Podría decirse que esta es un área en la que los Algoritmos Evolutivos (AE) se benefician de su relación con la biología, ya que la biología proporciona una fuente de información lista sobre cómo representar estructuras complejas de una manera evolutiva.
La Programación Evolutiva (PE) es una estrategia de optimización estocástica similar a los Algoritmos Genéticos (AG), pero hacen un énfasis específico en los operadores genéticos tal y como se observan en la naturaleza y en la estructura de datos que utilizan adaptada al problema. Por esto, a diferencia de los AG, la PE no es restrictiva en cuanto a la representación del problema. Mientras que, en los AG, es necesario una codificación de las soluciones del problema; en la PE, tal representación se hace de forma directa.
La Programación Evolutiva difiere de los algoritmos genéticos estándar en que el enfoque está en el comportamiento de los individuos, por lo que no se utiliza ningún cruce a favor de la mutación. El comportamiento se modela mediante parámetros de estrategia a partir de distribuciones. En términos de aplicación, la Programación Evolutiva se usa más comúnmente en entornos restringidos como programación y enrutamiento, sistemas de energía y sistemas de diseño.
Los Algoritmos Genéticos (AG) y la Programación Evolutiva (PE) son dos de las metodologías más importantes utilizadas satisfactoriamente para la solución de problemas de optimización de difíciles combinaciones, dentro de los Algoritmos Evolutivos. Su principal diferencia radica en que los AG utilizan los operadores cruzamiento y mutación, con el cruzamiento como operador primario de búsqueda mientras que la PE utiliza solamente la mutación, sin el cruzamiento. La mayoría de los investigadores posteriores a la mitad de la década de los 90 - no obstante, su relativa poca aplicación - consideran a la Programación Evolutiva mucho más simple, rápida y eficiente que los Algoritmos Genéticos.
El esquema original de la Evolución Diferencial (ED) ha sido satisfactoriamente extendido por varios autores con la intención de mejorar su robustez, esto es, su capacidad de resolver problemas con diferentes características. Dentro de estas extensiones sobresalen las que proponen la auto-adaptación de los parámetros y estrategias que influyen en el comportamiento del algoritmo. En la literatura varias propuestas interesantes incluyen de una forma u otra auto-adaptación. De manera general, la mayoría de estas ampliaciones, superan en precisión a la versión estándar de la ED en problemas estacionarios, sin embargo, no garantizan nunca que se encuentre una solución óptima (Novoa, et al., 2014).
La ED es el único algoritmo evolutivo que utiliza información direccional, cuyo uso es vital pues permite la adopción de un enfoque "exhaustivo o codicioso" al dirigirse hacia la dirección del vector objetivo. De esta forma, la evolución diferencial encontrará un mínimo más rápido que los otros algoritmos evolutivos; sin embargo, no se garantiza que dicho mínimo sea un óptimo global o bueno, pues la exploración es deficiente. Como resultado, la evolución diferencial supera a los algoritmos evolutivos estándar cuando el problema de optimización tiene solo uno o un par de óptimos locales; sin embargo, cuando el espacio de entrada tiene muchos óptimos locales, la evolución diferencial debería ser su último recurso (Morgan, 2021).
Una posible limitación de muchos algoritmos evolutivos - en comparación con los procesos biológicos - es su clara falta de distinción genotipo-fenotipo.
Los Algoritmos Evolutivos Multiobjetivos (AEMO), que generalizan los Algoritmos Evolutivos (AE) para casos de objetivos múltiples y los algoritmos meméticos (AM), que combinan los Algoritmos Evolutivos con la Búsqueda Local, también son populares, especialmente en aplicaciones prácticas (Corne & Lones, 2018).
Conclusiones
La optimización de la reconfiguración de redes, como la mayoría de los procesos industriales implican no linealidades dinámicas, incertidumbres y restricciones. Los Algoritmos Evolutivos están entre las muchas y diversas técnicas de optimización utilizadas en la solución de la amplia variedad de problemas de optimización en la industria.
Los investigadores han desarrollado los conceptos de estrategias evolutivas desde sus conceptos básicos, hasta la incorporación de conceptos más elaborados. Las Estrategias Evolutivas basan su operación en tres elementos: la selección, la recombinación y mutación. La selección de los mejores individuos se basa en la robustez de cada uno de ellos (selección del mejor) sin perder de vista la varianza (herramienta de mutación) que produjo a estos individuos óptimos, la cual se emplea a su vez para direccionar la producción de nuevas varianzas que se utilizarán para mutar los individuos de las siguientes generaciones. Estos conceptos marcan la tendencia de las estrategias evolutivas para la optimización de problemas multi variables. Los problemas con grandes espacios de búsqueda y de naturaleza combinatoria, son candidatos para aplicar las EE. Esta particularidad es una de las motivaciones para la aplicación de estas técnicas para la solución del problema de reconfiguración de red.
Cuando no se puede usar un algoritmo determinado en un problema dado, uno de los Algoritmos Evolutivos será una buena opción. Por supuesto, considerando los problemas que pueden enfrentarse: Convergencia prematura y la compensación óptima entre las propiedades de exploración y explotación de EA. Los valores de los parámetros de EA que son "buenos" en un problema no pueden ser suficientes en otro. Consecuentemente, la búsqueda de nuevas técnicas en áreas como el ajuste automático y el control de parámetros adaptativos sigue siendo un tema candente en los EA.
Los Algoritmos Evolutivos y sus múltiples tipos se han convertido en una prometedora área en la solución de un amplio rango de problemas y en una metodología popular de solución de problemas de optimización. El campo de la computación evolutiva ha logrado un estado de alguna madurez. Existen varias conferencias internacionales sobe el tema bien establecidas y que atraen a cientos de participantes. Además, existen muchos talleres, sesiones especiales y conferencias locales cada año, en todo el mundo. De hecho, la evolución por selección natural ha sido denominada la mejor idea siempre (Chu, 2014). No obstante, necesitar otro siglo y el desarrollo de la computación antes que los investigadores se interesaran en la simulación de procesos de la evolución natural.
Como tendencias futuras de los Algoritmos Evolutivos (AE) pueden mencionarse: La hibridación de dos o más algoritmos; el interés en los Algoritmos Meméticos y los diseños de implementación fácil para corridas en paralelo en la optimización de funciones de dominios de dimensiones elevadas para la solución de problemas reales, de gran complejidad y que exigen reducir las cargas computacionales. Otro importante tema en las aplicaciones industriales de los Algoritmos Evolutivos, es la adecuada definición de la función objetivo. Los problemas industriales son muy complejos, por lo tanto, la definición de un buen modelo matemático (buena función objetivo para los AE) para un proceso industrial determinado, continúa siendo aún, una tarea muy demandada.
En la optimización de la reconfiguración de redes de distribución eléctrica, la mayoría de los problemas prácticos están asociados con una o varias restricciones. Los problemas de optimización restringida son bastante difíciles de resolver debido a su complejidad y alta no linealidad. En los últimos años, la Evolución Diferencial (ED) ha ganado un interés creciente para resolver problemas de optimización en este y en otros campos de ingeniería. Hoy en día, se considera uno de los algoritmos de optimización más populares para problemas de optimización continua (Morgan, 2021).
Cuando los Algoritmos Genéticos (AG) son aplicados a la reconfiguración de redes - no obstante, su relativa simplicidad para formular problemas matemáticamente complejos y considerarse mejores que los algoritmos heurísticos - aparece la necesidad de realizar comprobaciones de radialidad que recargan notablemente su algoritmo matemático. También se ha planteado que los métodos basados en AG son mejores que los algoritmos heurísticos tradicionales en la obtención del óptimo global (González, et al., 2016).
Puede resultar difícil seleccionar qué AE utilizar para un problema particular debido a que existen muchos diferentes tipos y relativamente escasa orientación que los compare. En la práctica, es necesario analizar y estudiar bien diferentes AE para determinar el que mejor se ajuste al problema, especialmente, cuando el problema es poco comprendido.
El artículo realiza una exploración científica de los Algoritmos Evolutivos (AE) ubicándolos en los métodos de búsqueda y optimización en general y en los de optimización de la reconfiguración de redes de distribución, los clasifica en el dominio de la Computación Evolutiva (CE) y fundamenta las generalidades de los más populares: Estrategias Evolutivas (EE), Algoritmos Genéticos (AG), Programación Genética (PG), Programación Evolutiva (PE) y Evolución Diferencial (ED) y realiza una comparación entre ellos. Resume, además, las contribuciones más importantes y el número de publicaciones sobre optimización de la reconfiguración de redes registradas en Google Académico y en la Web of Science.
Se considera que, en el futuro, se desarrollarán nuevos Algoritmos Evolutivos y los problemas de investigación vinculados a ellos, siempre serán un tópico “caliente” para los investigadores.
