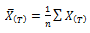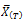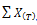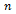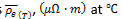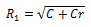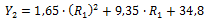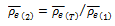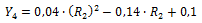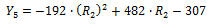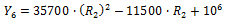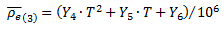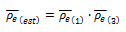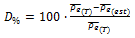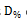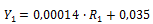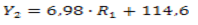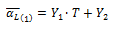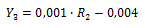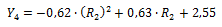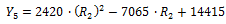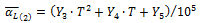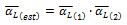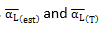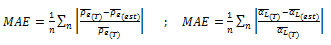Introduction
Currently, the high cost in money and time linked to experimental tests for the evaluation of thermo physical properties of steels, has established the preference for the use of predictive models in order to avoid this complex task (Şahinoğlu & Rafighi, 2021).
When a large set of experimental data is available, artificial neural network (ANN) and finite element method (FEM) have been widely used in predictive modeling (Min, et al., 2020). A detailed review of the available and known literature shows that currently reported methods for estimating thermo physical properties of steels, although they include dependence on composition and temperatures, only have the ability to predict a unitary property of the selected steel (Shi, et al., 2018).
Using ANN, a model was created to predict the thermal conductivity of AISI-SAE1045 steel, establishing its dependence on temperature and composition. The prediction was based on a Bayesian statistical framework (Peet, Hasan & Bhadeshia, 2011).
Other studies were focused on the prediction of three-dimensional heat flow, as well as heat transfer coefficient distributions in space and time. FEM techniques are used to study the phase transformation and its impact on the average heat transfer coefficient in the heat treatment of forged steels (Khodabakhshi & Kazeminezhad, 2011; Bouissa, et al., 2019).
The dependence between the temperature and the mean heat transfer coefficient, as well as the cooling curves, the cooling rate curves and the distortion are predicted from the iterative modification of the concentrated heat capacity method and the heat transfer method. reverse heat in AISI-304 and AISI-1045 steels. To study the density variation of AISI-316L steel, the laser power, speed and scanning spacing were used during selective laser melting, using variance analysis for this purpose (Miranda, et al., 2016).
Five different numerical algorithms, including Heat Balance Method (HBM), Revised Heat Balance Method (R-HBM), Nonlinear Beck Estimation Method (BEM), Inverse Finite Element Optimization Method (FIOM) and the finite element optimization method (FOM) were used for the prediction of thermal conductivity in carbon steels (Somasundharam & Reddy, 2020).
Another work considers that the simultaneous estimation of the thermal conductivity is dependent on the temperature and the specific heat, assuming that this dependence is a parametric variation of the temperature, estimating the properties from the solution of the inverse problem (Wang & Adachi, 2019). With this objective, it is established that the prediction models must take the composition as the only input data (Lieth, et al., 2021).
Recently, a combined model was presented that includes the influence of composition and temperature on the variation of thermal conductivity in austenitic stainless steels (Narayana, et al., 2020). Other methods, to perform prediction correlations, use a multiple linear regression analysis in the estimation of the thermal conductivity of carbon steels (Zheng, et al., 2020). A similar study proposes a nonlinear regression equation to predict the cooling limit curve and thermal conductivity in carbon steels (Borisade, et al., 2021). Other researchers, through the use of ANN, take the composition (Si, Cr, Ni, Mo) in alloyed steels as a starting point to estimate the cooling curve required in the heat treatment, also facilitating the evaluation of thermal conductivity (Xie, et al., 2021).
Therefore, despite the existence of multiple investigative works on the subject, none of them presents a methodology that allows the prediction of an extended group of thermo physical properties of a wide range of steels, nor does it establish the dependence of these properties with composition and temperature, so the existence of a prediction method that resolves these limitations would be extremely useful (Gomez, et al., 2020; Li, et al., 2021).
In this study, a prediction method based on the adjustment and validation of experimental data is presented through the mathematical application of the residual method based on the progressive adjustment of functions (PAF), which will allow estimating two thermo physical properties (electrical resistivity and linear thermal expansion) corresponding to 32 classes of steels with a composition (C, Mn, P, S, Si, Ni, Cr, Mo, V), operating in a temperature range from 0oC to 800oC.
Materials and methods
2.1 Data processing using the progressive adjustment method.
The available experimental data relate the influence of temperature and composition on the variation of the studied thermo physical properties. In collaboration with the School of Engineering and Applied Science, Khazar University (Azerbaijan), the experimental data used in the adjustment and validation of the models were obtained. Table 1 summarizes the number of available experimental data for each value of temperature and thermo physical property studied, while Table 2 summarizes the validity range of the proposed method.
The modeling is carried out using the method of progressive function adjustment (APF). The analysis is too expensive and complex, and for reasons of space it cannot be fully shown here, however, as the applied procedure is identical for the two thermo physical properties, the modeling of the electrical resistivity will be detailed, while for the thermal expansion linear only the equations obtained, adjustments and validation will be given.
For electrical resistivity, once the experimental data has been grouped into the 32 AISI-SAE classifications covered (see table 2), the average value is obtained for each AISI-SAE steel and temperature range, using Equation 1.
Equation 1. Mean values calculations
where:
is the average of the property or composition for each steel studied at temperature T. |
|
is the sum of all available values of each property or composition in each steel studied at temperature T. |
|
is the number of samples available in each steel studied at temperature T. |
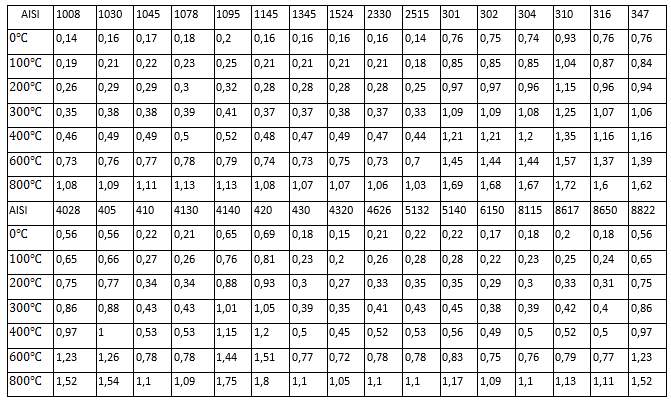
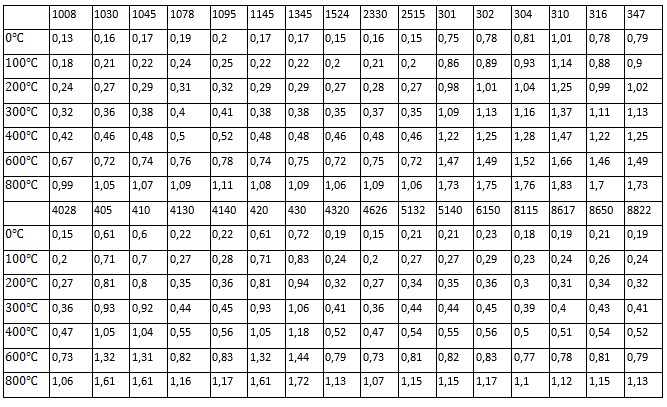
The average values obtained with Equation 1 are given in table 3, while table 4 summarizes the average composition per steel.
From the average composition (see table 4), the composition factors R 1 y R 2 , are determined, given in Equations 2 and 3, (Camaraza-Medina, Hernandez-Guerrero & Luviano-Ortiz, 2021a).
Equation 2. Calculation of the composition factor R 1.
Equation 3. Calculation of the composition factor R 2 .
In Equations 2 and 3, the composition values are given in %.
Table 4 - Average composition values per steel studied, (%)
| AISI | 1008 | 1030 | 1045 | 1078 | 1095 | 1145 | 1345 | 1524 | 2330 | 2515 | 301 | 302 | 304 | 310 | 316 | 347 |
| C | 0,08 | 0,31 | 0,47 | 0,78 | 0,98 | 0,46 | 0,41 | 0,22 | 0,33 | 0,15 | 0,13 | 0,13 | 0,07 | 0,23 | 0,07 | 0,08 |
| Mn | 0,4 | 0,7 | 0,75 | 0,45 | 0,39 | 0,84 | 1,72 | 1,49 | 0,69 | 0,49 | 1,89 | 1,89 | 1,89 | 1,89 | 1,89 | 0,4 |
| P | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 |
| S | 0,04 | 0,04 | 0,04 | 0,04 | 0,04 | 0,06 | 0,03 | 0,04 | 0,03 | 0,03 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,04 |
| Si | - | - | - | - | - | - | 0,26 | - | 0,28 | 0,28 | 0,64 | 0,64 | 0,64 | 1,31 | 0,64 | - |
| Ni | - | - | - | - | - | - | - | - | 3,47 | 4,97 | 7 | 6,7 | 9,06 | 20,31 | 11,66 | - |
| Cr | - | - | - | - | - | - | - | - | - | - | 17,2 | 18,2 | 19,2 | 24 | 17 | - |
| Mo | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 2,58 | - |
| V | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| AISI | 4028 | 405 | 410 | 4130 | 4140 | 420 | 430 | 4320 | 4626 | 5132 | 5140 | 6150 | 8115 | 8617 | 8650 | 8822 |
| C | 0,07 | 0,28 | 0,06 | 0,13 | 0,31 | 0,41 | 0,13 | 0,1 | 0,2 | 0,27 | 0,33 | 0,41 | 0,51 | 0,16 | 0,18 | 0,51 |
| Mn | 1,89 | 0,79 | 0,84 | 0,84 | 0,49 | 0,87 | 0,87 | 0,87 | 0,54 | 0,54 | 0,69 | 0,78 | 0,8 | 0,79 | 0,79 | 0,87 |
| P | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,04 | 0,03 | 0,03 | 0,03 |
| S | 0,02 | 0,04 | 0,03 | 0,02 | 0,03 | 0,03 | 0,02 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,04 | 0,03 | 0,03 | 0,03 |
| Si | 0,64 | 0,28 | 0,77 | 0,77 | 0,28 | 0,28 | 0,86 | 0,86 | 0,24 | 0,23 | 0,28 | 0,28 | 0,28 | 0,23 | 0,28 | 0,28 |
| Ni | 10,66 | - | - | 0,61 | - | - | - | 0,61 | 1,8 | 0,83 | - | - | - | 0,29 | 0,53 | 0,53 |
| Cr | 18,2 | - | 13,3 | 12,7 | 0,98 | 0,98 | 13,2 | 17,2 | 0,52 | 0,9 | 0,8 | 0,98 | 0,42 | 0,52 | 0,52 | |
| Mo | - | 0,26 | - | - | 0,21 | 0,21 | - | - | 0,26 | 0,21 | - | - | - | 0,12 | 0,2 | 0,2 |
| V | - | - | - | - | - | - | - | - | - | - | - | - | 0,13 | - | - | - |
The PAF method is generated from a base correlation, to which corrections are made through linear or polynomial functions (Camaraza-Medina, 2021). To obtain the base correlation, the method of least squares is applied to the mean values given in Table 3, obtaining a polynomial in the form 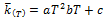 per steel, (it can be used a linear function, but the predictive capacity of the model is reduced). Table 5 summarizes the parameters a, b and c for each correlation performed, the R
2
, as well as the respective composition values R
1
estimated with Equation 2, (see table 4 for the composition values used).
per steel, (it can be used a linear function, but the predictive capacity of the model is reduced). Table 5 summarizes the parameters a, b and c for each correlation performed, the R
2
, as well as the respective composition values R
1
estimated with Equation 2, (see table 4 for the composition values used).
Table 5 - Correlation of the mean values for the first adjustment.
| AISI- SAE |
|
|
AISI- SAE |
|
|
||||||
| 1008 | 0,283 | 0,095 | 41,52 | 14091 | 0,99 | 4028 | 0,529 | 0,091 | 40,32 | 14953 | 0,98 |
| 1030 | 0,557 | 0,086 | 47,92 | 15921 | 0,98 | 405 | 3,651 | 0,042 | 86,95 | 55697 | 1,0 |
| 1045 | 0,686 | 0,092 | 44,02 | 16995 | 1,0 | 410 | 3,576 | 0,032 | 96,9 | 56147 | 0,99 |
| 1078 | 0,883 | 0,094 | 42,82 | 18111 | 1,0 | 4130 | 1,136 | 0,083 | 43,69 | 22128 | 1,0 |
| 1095 | 0,99 | 0,088 | 45,84 | 19613 | 1,0 | 4140 | 1,179 | 0,075 | 49,62 | 20897 | 0,98 |
| 1145 | 0,678 | 0,089 | 42,05 | 16385 | 1,0 | 420 | 3,646 | 0,035 | 110,2 | 64742 | 1,0 |
| 1345 | 0,64 | 0,09 | 41,58 | 16017 | 1,0 | 430 | 4,155 | 0,029 | 117,0 | 68638 | 1,0 |
| 1524 | 0,469 | 0,079 | 51,61 | 15273 | 0.98 | 4320 | 0,849 | 0,089 | 44,06 | 18114 | 1,0 |
| 2330 | 0,57 | 0,089 | 41,5 | 16158 | 1,0 | 4626 | 0,52 | 0,09 | 40,23 | 14862 | 0,98 |
| 2515 | 0,387 | 0,091 | 38,74 | 13655 | 1,0 | 5132 | 1,109 | 0,087 | 42,15 | 20947 | 0,99 |
| 301 | 4,162 | 0,008 | 112,0 | 74737 | 1,0 | 5140 | 1,1 | 0,08 | 45,67 | 22131 | 0,99 |
| 302 | 4,28 | 0,009 | 110,5 | 74678 | 0,99 | 6150 | 1,221 | 0,086 | 48,9 | 22192 | 0,99 |
| 304 | 4,387 | 0,006 | 112,5 | 73855 | 1,0 | 8115 | 0,762 | 0,089 | 43,05 | 17217 | 1,0 |
| 310 | 4,922 | -0,019 | 115,8 | 92523 | 1,0 | 8617 | 0,837 | 0,089 | 43,96 | 17985 | 1,0 |
| 316 | 4,132 | 0,01 | 96,59 | 76428 | 0,99 | 8650 | 1,015 | 0,088 | 46,18 | 1988 | 1,0 |
| 347 | 4,274 | 0,017 | 94,7 | 75535 | 0,98 | 8822 | 0,866 | 0,089 | 44,27 | 18296 | 1,0 |
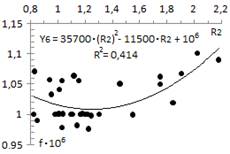
To establish the base function in the prediction of electrical resistivity, all the values a, b and c are individually correlated with R 1 (see table 5), thus obtaining a first approximation to describe the dependence between temperature and thermal conductivity, for any of the AISI-SAE steels evaluated. The correlations obtained are graphically represented in Fig 1 , 2, 3.
Correlations plotted in Fig 1, 2 and 3 are given by:
Equation 4. Obtaining the adjustment parameter 1 of the APF.
Equation 5. Obtaining the adjustment parameter 2 of the APF.
Equation 6. Obtaining the adjustment parameter 3 of the APF.
The function taken for the first progressive adjustment was a second order polynomial; therefore, Equations 4, 5 and 6 can be summarized in Equation 7:
Equation 7. Calculation of electrical resistivity in the first approximation.
Equation 7 is the first approximation or base function of the progressive function adjustment. To carry out the second step of the adjustment, the values of are calculated using equation 7 for each interval shown in Table 3 and subsequently a quotient is established with the experimental values, thus defining the required setting value. Mathematically this is described by Equation 8:
Equation 8. Calculation of the adjustment residual value for the second round of APF.
The results obtained with the use of equation 8 are summarized in table 6.
| AISI- SAE | 00C | 1000C | 2000C | 3000C | 4000C | 6000C | 8000C |
| 1008 | 1,106 | 1,103 | 1,098 | 1,093 | 1,088 | 1,082 | 1,077 |
| 1030 | 1,056 | 1,064 | 1,071 | 1,073 | 1,072 | 1,057 | 1,043 |
| 1045 | 1,032 | 1,036 | 1,038 | 1,039 | 1,039 | 1,039 | 1,039 |
| 1078 | 0,992 | 0,991 | 0,995 | 1,0 | 1,006 | 1,017 | 1,025 |
| 1095 | 1,0 | 1,001 | 1,003 | 1,004 | 1,005 | 1,006 | 1,007 |
| 1145 | 1,0 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 1345 | 1,0 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 1524 | 1,083 | 1,091 | 1,097 | 1,101 | 1,095 | 1,066 | 1,035 |
| 2330 | 1,065 | 1,05 | 1,039 | 1,032 | 1,026 | 1,02 | 1,011 |
| 2515 | 0,999 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 301 | 1,091 | 1,068 | 1,071 | 1,068 | 1,062 | 1,04 | 1,013 |
| 302 | 1,049 | 1,038 | 1,034 | 1,034 | 1,03 | 1,015 | 0,995 |
| 304 | 1,003 | 1,002 | 1,003 | 1,003 | 1,002 | 0,993 | 0,979 |
| 310 | 1,053 | 1,031 | 1,017 | 1,001 | 0,987 | 0,98 | 0,939 |
| 316 | 1,101 | 1,088 | 1,061 | 1,05 | 1,02 | 0,984 | 0,96 |
| 347 | 1,068 | 1,025 | 1,011 | 1,011 | 0,993 | 0,98 | 0,957 |
| 4028 | 1,0 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 405 | 0,94 | 0,947 | 0,947 | 0,953 | 0,95 | 0,959 | 0,964 |
| 410 | 0,976 | 0,984 | 0,992 | 0,996 | 1,0 | 0,994 | 0,985 |
| 4130 | 1,043 | 1,019 | 1,001 | 0,988 | 0,98 | 0,969 | 0,964 |
| 4140 | 0,969 | 0,968 | 0,97 | 0,97 | 0,968 | 0,954 | 0,944 |
| 420 | 1,101 | 1,109 | 1,117 | 1,119 | 1,125 | 1,124 | 1,111 |
| 430 | 1,001 | 1,013 | 1,031 | 1,03 | 1,054 | 1,083 | 1,079 |
| 4320 | 1,0 | 1,001 | 1,002 | 1,004 | 1,005 | 1,006 | 1,007 |
| 4626 | 1,0 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 5132 | 1,004 | 0,985 | 0,974 | 0,969 | 0,967 | 0,967 | 0,97 |
| 5140 | 1,053 | 1,038 | 1,027 | 1,006 | 0,992 | 0,976 | 0,968 |
| 6150 | 1,001 | 1,002 | 1,003 | 1,004 | 1,005 | 1,007 | 1,007 |
| 8115 | 1,0 | 1,001 | 1,002 | 1,003 | 1,004 | 1,006 | 1,007 |
| 8617 | 1,0 | 1,001 | 1,002 | 1,004 | 1,005 | 1,006 | 1,007 |
| 8650 | 1,001 | 1,002 | 1,003 | 1,004 | 1,005 | 1,006 | 1,007 |
| 8822 | 1,0 | 1,001 | 1,002 | 1,004 | 1,005 | 1,006 | 1,007 |
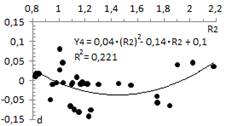
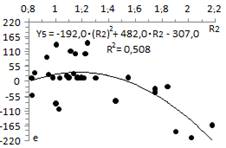
In table 6, using the method of least squares, a correlation is obtained in the form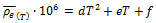 for each steel. Table 7 summarizes the parameters d, e and f for each correlation and their R
2
values, as well as the R
2
factors estimated using Equation 3, (see table 4 for the composition per steel). To define the second correction (see table 7), the values d, e and f are individually correlated with R
2
. The obtained fits are provided in Fig 4, 5 and 6.
for each steel. Table 7 summarizes the parameters d, e and f for each correlation and their R
2
values, as well as the R
2
factors estimated using Equation 3, (see table 4 for the composition per steel). To define the second correction (see table 7), the values d, e and f are individually correlated with R
2
. The obtained fits are provided in Fig 4, 5 and 6.
Table 7 - Correlation of the mean values for the second adjustment.
| AISI- SAE |
|
R2 | AISI- SAE |
|
|
||||||
| 1008 | 0,828 | 0,016 | -50,82 | 1106737 | 1,00 | 4028 | 1,088 | -0,006 | 14,21 | 999539 | 1,00 |
| 1030 | 0,937 | -0,137 | 89,91 | 1056883 | 0,96 | 405 | 1,137 | -0,002 | 29,34 | 941683 | 0,94 |
| 1045 | 0,952 | -0,022 | 24,74 | 1032956 | 0,97 | 410 | 1,227 | -0,113 | 101,3 | 975850 | 0,98 |
| 1078 | 0,849 | 0,017 | 32,4 | 989545 | 0,98 | 4130 | 1,01 | 0,156 | -218,2 | 1040832 | 0,99 |
| 1095 | 0,824 | -0,006 | 13,22 | 1000325 | 1,00 | 4140 | 1,092 | -0,066 | 20,6 | 968398 | 0,97 |
| 1145 | 0,982 | -0,006 | 13,64 | 999799 | 1,00 | 420 | 1,155 | -0,112 | 102,8 | 1100620 | 0,98 |
| 1345 | 1,194 | -0,006 | 13,87 | 999710 | 1,00 | 430 | 1,245 | -0,076 | 168,3 | 997889 | 0,95 |
| 1524 | 1,118 | -0,22 | 112,8 | 1083341 | 0,98 | 4320 | 1,305 | -0,006 | 13,45 | 1000070 | 1,00 |
| 2330 | 1,456 | 0,079 | -125,7 | 1063315 | 0,99 | 4626 | 1,169 | -0,006 | 14,19 | 999549 | 1,00 |
| 2515 | 1,552 | -0,007 | 14,66 | 999362 | 1,00 | 5132 | 1,007 | 0,135 | -142,9 | 1000587 | 0,95 |
| 301 | 1,759 | -0,058 | -40,37 | 1083664 | 0,95 | 5140 | 1,028 | 0,101 | -192,4 | 1055817 | 0,99 |
| 302 | 1,745 | -0,042 | -26,99 | 1044803 | 0,97 | 6150 | 1,036 | -0,006 | 13,14 | 1000755 | 1,00 |
| 304 | 1,847 | -0,065 | 24,53 | 1001557 | 0,99 | 8115 | 1,105 | -0,006 | 13,64 | 999913 | 1,00 |
| 310 | 2,203 | 0,035 | -157,9 | 1048715 | 0,97 | 8617 | 1,168 | -0,006 | 13,26 | 1000081 | 1,00 |
| 316 | 2,025 | 0,045 | -221,1 | 1105170 | 0,99 | 8650 | 1,18 | -0,005 | 12,98 | 1000428 | 1,00 |
| 347 | 1,908 | 0,11 | -207,0 | 1057128 | 0,94 | 8822 | 1,199 | -0,005 | 13,23 | 1000135 | 1,00 |
The correlations plotted in Figures 4, 5 y 6 are given by:
Equation 9. Obtaining the adjustment parameter 4 of the APF.
Equation 10. Obtaining the adjustment parameter 5 of the APF.
Equation 11. Obtaining the adjustment parameter 6 of the APF.
The function taken for the second progressive adjustment was a second order polynomial, therefore, Equations 9, 10 and 11 can be summarized in Equation 7:
Equation 12. Calculation of electrical resistivity in the second approximation.
The electrical resistivity can then be estimated from the product of the two progressive adjustments made, (Equations 7 and 12), obtaining that:
Equation 13. Calculation of the estimated electrical resistivity.
The electrical resistivity values computed using Equation 13 are given in the table 8.
The percentage of deviation (error) computed with the proposed method is obtained through Equation 14 (Camaraza-Medina, Guerrero-Hernandez & Luviano-Ortiz, 2021b):
Equation 14. Calculation of the correlation error of the proposed method (Equation 13).
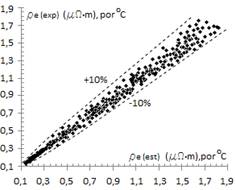
Table 9 summarizes values obtained by comparing the experimental data tabulated in Table 3 with the results obtained through Equation 14. Figure 7 correlates the 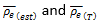 values with an error band of 10%.
values with an error band of 10%.
Applying a procedure analogous to the electrical resistivity, a methodology is established to estimate linear thermal expansion, which is given by Equations 15, 16, 17, 18, 19, 20, 21 and 22:
Equation 15. Obtaining the adjustment parameter 1 of the APF.
Equation 16. Obtaining the adjustment parameter 2 of the APF.
Equation 17. Calculation of linear thermal expansion in the first approximation.
Equation 18. Obtaining the adjustment parameter 3 of the APF.
Equation 19. Obtaining the adjustment parameter 4 of the APF.
Equation 20. Obtaining the adjustment parameter 5 of the APF.
Equation 21. Calculation of linear thermal expansion in the second approximation.
Equation 22. Calculation of the estimated linear thermal expansion.
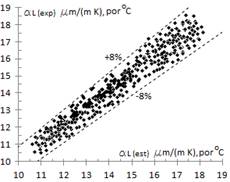
In the figure 8, values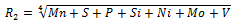 are correlated with an error band of 8%.
are correlated with an error band of 8%.
Results and discussion
Estimation of the dispersion obtaining in the APF method application.
Table 10 gives the values of maximum error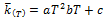 and mean absolute error (MAE) obtained by correlating Equations 13 and 22 with the available experimental data. The MAE values are estimated from Equation 23, (Camaraza-Medina, et al., 2020):
and mean absolute error (MAE) obtained by correlating Equations 13 and 22 with the available experimental data. The MAE values are estimated from Equation 23, (Camaraza-Medina, et al., 2020):
Equation 23. Estimation of the MAE values.
For the electrical resistivity, the most unfavorable dispersion index is obtained for AISI-SAE 405 steel, with a 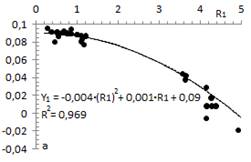 of -9.9% at a temperature of 100oC and an MAE of 8.2% in the 81.9% of available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1095 steel, with a
of -9.9% at a temperature of 100oC and an MAE of 8.2% in the 81.9% of available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1095 steel, with a 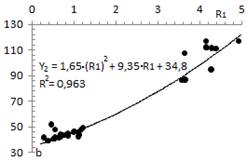 of 1.7% at a temperature of 800oC, with an MAE of 0.8% in the 85.1% of the available experimental data.
of 1.7% at a temperature of 800oC, with an MAE of 0.8% in the 85.1% of the available experimental data.
In the linear thermal expansion modeling, the most unfavorable dispersion index is obtained for AISI-SAE 1524 steel, with a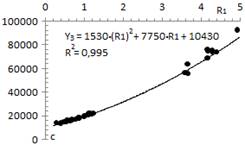 of 7.0% at a temperature of 400oC and an MAE of 6.1% in the 79.6% of the available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1030 steel, with a
of 7.0% at a temperature of 400oC and an MAE of 6.1% in the 79.6% of the available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1030 steel, with a 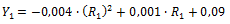 of 1.3% at a temperature of 400oC and an MAE of 0.9% in the 83.4% of the available data.
of 1.3% at a temperature of 400oC and an MAE of 0.9% in the 83.4% of the available data.
Conclusions
A predictive method is presented to estimate the electrical resistivity and linear thermal expansion in 32 types of steels with a known composition (C, Mn, P, S, Si, Ni, Cr, Mo, V) and operating in temperature ranges from 0oC to 800oC. The proposed models were verified by comparison with available experimental data.
In the electrical resistivity modeling, the most unfavorable dispersion index is obtained for AISI-SAE 405 steel, with a 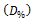 of -9.9% at a temperature of 100oC and an MAE of 8.2% in the 81.9% of available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1095 steel, with a
of -9.9% at a temperature of 100oC and an MAE of 8.2% in the 81.9% of available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1095 steel, with a 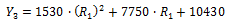 of 1.7% at a temperature of 800oC, with an MAE of 0.8% in the 85.1% of the available experimental data. In the linear thermal expansion modeling, the most unfavorable dispersion index is obtained for AISI-SAE 1524 steel, with a
of 1.7% at a temperature of 800oC, with an MAE of 0.8% in the 85.1% of the available experimental data. In the linear thermal expansion modeling, the most unfavorable dispersion index is obtained for AISI-SAE 1524 steel, with a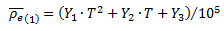 of 7.0% at a temperature of 400oC and an MAE of 6.1% in the 79.6% of the available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1030 steel, with a
of 7.0% at a temperature of 400oC and an MAE of 6.1% in the 79.6% of the available experimental data. The best fit is achieved in the correlation of the properties of AISI-SAE 1030 steel, with a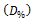 of 1.3% at a temperature of 400oC and an MAE of 0.9% in the 83.4% of the available data.
of 1.3% at a temperature of 400oC and an MAE of 0.9% in the 83.4% of the available data.
In all cases, the agreement of the proposed model with the available experimental data is good enough to be considered satisfactory for practical design. Regarding the elements of the study presented, there is no evidence of similar expressions in the available and known literature, for this reason, the proposal presented is considered as a scientific novelty in the field of knowledge addressed.