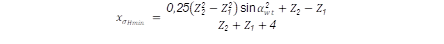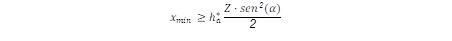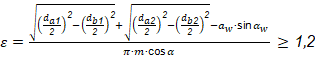Artículo original

FACTOR DE CORRECCIÓN ÓPTIMO PARA MINIMIZAR LAS TENSIONES DE CONTACTO EN ENGRANAJES CILÍNDRICOS

OPTIMAL SHIFT PROFILE MODIFICATION TO MINIMIZE CONTACT STRESSES IN CYLINDRICAL GEARS

0000-0001-8907-7511Eduardo Miguel Fírvida Donéstevez¹  , 0000-0002-7774-8653Ángel Silvio Machado Rodríguez^{1  *}  , 0000-0003-0541-0191Jorge Laureano Moya Rodríguez² 

¹Departamento de Ingeniería Mecánica. Facultad de Ingeniería Mecánica e Industrial. Universidad Central “Marta Abreu” de Las Villas. Carretera a Camajuaní km 5 ½, Santa Clara, Villa Clara, Cuba.

²Universidade Federal da Bahia. Escola Politécnica. Programa de pós-Graduação em Engenharia Industrial. Departamento de Engenharia Química. San Salvador de Bahia, Brasil.

RESUMEN

Introducción:

El diseño de las transmisiones por engranajes cilíndricos continúa siendo un tema de gran importancia. Con el creciente desarrollo de los métodos computacionales, muchos autores han trabajado en la optimización de dichas transmisiones con el objetivo fundamental de aumentar su capacidad de carga y/o alargar su vida útil.

Objetivo:

Evaluar la influencia del factor de corrección sobre las tensiones de contacto en el perfil del diente, considerando las restricciones geométricas y determinar el factor de corrección para mínimas tensiones de contacto.

Materiales y Métodos:

Por la formulación de la teoría de Hertz Budynas−Nisbett para dos cilindros en contacto, se formula el problema de optimización con restricciones, al cual se le da solución por diferentes métodos de optimización, se evalúa un método de solución elaborado por los autores.

Resultados y Discusión:

Se valida el método propuesto a partir de la comparación de los factores de corrección obtenidos con los factores recomendados por el programa de diseño KISSSoft-v2014, evaluadas para las normas (AGMA, 2004; ISO 6336-2, 2006) implementadas por los autores.

Conclusiones:

Se obtiene el valor del factor de corrección, logrando una mejor distribución de las tensiones de contacto sobre el diente en la zona de trabajo. El método numérico presentado, obtiene los mismos resultados que los métodos clásicos de optimización, validando su uso en la solución del problema.

Palabras-clave: engranajes cilíndricos; factor de corrección; optimización; tensiones de contacto

ABSTRACT

Introduction:

Cylindrical gear transmissions design continues to be a great importance topic. With the increasing development of computational methods, many authors have worked on such transmissions optimization with increasing their load capacity and / or extending their useful life as fundamental objective.

Objective:

To evaluate the influence of the correction factor over contact stresses in tooth profile, considering the geometric constraints and to determine correction factor for minimum contact stresses.

Materials and Methods:

By formulating the Hertz Budynas − Nisbett theory for two cylinders in contact, the optimization problem is formulated with restrictions that are solved by different optimization methods, a solution method developed by the authors is evaluated.

Results and Discussion:

The proposed method is validated by the comparison of obtained correction factors, with its recommended by the KISSSoft-v2014 design program factors, evaluated for the standards (AGMA, 2004; ISO 6336-2, 2006) implemented by the authors

Conclusions:

Correction value factor is obtained, achieving a better distribution of contact stresses on tooth in work area. The numerical method presented, obtains the same results than classical optimization methods, validating its use in problem solution.

Key words: cylindrical gears; correction factor; optimization; contact stresses

INTRODUCCIÓN

El diseño de las transmisiones por engranajes cilíndricos metálicos continúa siendo un tema importante en la ingeniería debido al uso de estos elementos de máquina en las más disimiles aplicaciones. Durante años, los especialistas en esta actividad, han servido de apoyo a los distintos sectores de la industria que utilizan estos componentes, dando lugar a la aparición de normas técnicas, las cuales se han aplicado de manera general logrando aportar uniformidad y seguridad en el diseño de los mismos.

Con el continuo crecimiento de las exigencias técnicas hacia los engranajes debido al aumento de su capacidad de trabajo, han llevado a la necesidad de perfeccionar los métodos de cálculo y en particular, el desarrollo de métodos de selección óptima de sus parámetros. A la vez que existen discrepancias entre los valores de las tensiones de contacto en el flanco del diente calculados por las diferentes normas de diseño de engranajes existentes, a pesar de estar fundamentadas sobre la misma teoría sustentada sobre el modelo de dos cilindros en contacto planteado por Heinrich Hertz en 1882 (^{Budynas & Nisbett, 2012}; ^{Machado, 2000}) superponiendo cilindros a los perfiles evolventes de los dientes de los engranajes.

Uno de los métodos más utilizados por los ingenieros para la disminución de las tensiones de contacto y por tanto atenuar las fallas asociadas, es la utilización del factor de corrección. Debido a que las modificaciones del perfil afectan directamente las tensiones en los dientes y, por tanto, a la capacidad de carga y la estabilidad de la transmisión. Las normas disponibles como (^{DIN, 1964}; ^{IS 3756, 2002}; ^{ISO 6336-2, 2006}) recomiendan la selección de este factor, sin embargo, es sus valores son muy aproximado ya que generalmente se presentan en forma de gráficos o cuadros implícitos. Los autores (^{Gunay et al., 1996}; ^{Karadere y Yilmaz, 2018}; ^{Milera et al., 2017}), entre otros, hacen uso del método de simulación numérica (elementos finitos) para evaluar el comportamiento tensional de los dientes para varios factores de corrección, y validar la eficacia de este método como vía para la disminución de las tensiones en el flanco del diente. Mientras que otros (^{Rodríguez y Espinosa, 2000}; ^{Rodríguez et al., 2007}) mediante análisis geométricos de la transmisión brindan una expresión (ecuación 1) que corresponde al valor de corrección de altura necesarios para obtener el mínimo valor de tensiones de contacto, o lo que es lo mismo, la máxima resistencia a la picadura.

() 1

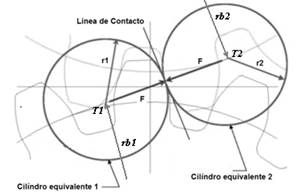
La formulación de dicha expresión parte de una deducción geométrica de la transmisión en la cual x σ Hmin representa el factor de corrección del piñón donde los cilindros teóricos en contacto son iguales (r1=r2, (Fig. 1)), para transmisiones con corrección de altura. La ecuación 1, no tiene en cuenta las restricciones geométricas del dentado comentadas por (^{Lemos y Delgado, 2007}; ^{Merritt, 1975}; ^{Rey, 2001}; ^{Rodríguez y Espinosa, 2000}; ^{Rodríguez et al., 2007}), las cuales deben ser chequeadas, según plantean los autores, y reajustar los valores de corrección obtenidos, de ser incumplidas alguna de las restricciones.

Otros trabajos (^{Caballero et al., 2013}; ^{Korta y Mundo, 2017}; ^{Marimuthu y Muthuveerappan, 2014}; ^{Milojevi´, 2013}) se centran en el uso de algoritmos de optimización en los cuales se incluye el factor de corrección como criterio de optimización entre otros parámetros. En estos casos tampoco se tienen en cuenta las restricciones geométricas de la transmisión las cuales pueden ser afectadas por el factor de corrección.

La solución del problema puede ser formulada como un problema de optimización, con restricciones, y resuelto por los métodos de optimización conocidos, donde la determinación de las tensiones de contacto puede ser evaluada por la norma requerida por el diseñador.

El objetivo del presente trabajo es evaluar la influencia del factor de corrección sobre las tensiones de contacto en el perfil del diente, considerando las restricciones geométricas y determinar el factor de corrección para mínimas tensiones de contacto.

MATERIALES Y MÉTODOS

2.1. Metodología

Las normas y métodos de diseño de las transmisiones por engranajes para atenuar la falla por picadura presentadas por: (^{Merritt, 1975}), (^{Estrems, 1998}), (^{AGMA, 2004}), (^{ISO 6336-2, 2006}), coinciden en que el modelo más aceptado para la determinación de las tensiones de contacto ( 𝜎 𝐻 ) se rige por la formulación de la teoría de Hertz Budynas−Nisbett para dos cilindros en contacto. La aplicación de dichos métodos formula una simplificación en la cual se sustituyen los perfiles evolventes de los dientes en contacto por dos cilindros, donde la suma de sus radios r1 y r2 (Fig. 1) es igual a la longitud de la línea teórica de engranaje T1T2.

Fig. 1 Modelo de Hertz para engranajes cilíndricos de dientes rectos 

En la (Fig. 2) se muestra la distribución de las tensiones de contacto en un diente engranado. Siempre que se garantice un factor de recubrimiento mayor que 1.2 (Ԑ ≥ 1.2), en el inicio y final del contacto la carga en el diente es distribuida entre dos pares engranados, de ahí que la zona de mayor nivel de tensiones sea la zona donde solo existe una pareja de dientes en contacto (zona 1 (Fig. 2)).

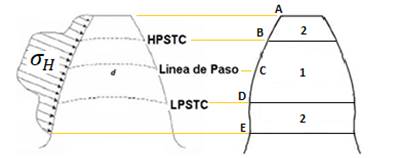
Fig. 2 Distribución de tensiones de contacto ( 𝜎 𝐻 ) sobre el flanco del diente, 1) Zona de contacto de un solo par de dientes. 2) Zona de contacto de más de un par de dientes. HPSTC) punto superior de contacto de un solo par de dientes. LPSTC) punto inferior de contacto de un solo par de dientes 

Cualquier modificación en la geometría del perfil del diente que disminuya la magnitud de las tensiones de contacto ( 𝜎 𝐻 ) reduce la posibilidad de aparición de la falla en el mismo y disminuye la tendencia a su destrucción. Es común utilizar el factor de corrección como vía para atenuar esta falla. Debido a que una correcta selección de los factores de corrección puede hacer la distribución de tensiones en el flanco del diente simétrica con respecto a su punto mínimo, mediante el desplazamiento de la línea práctica de engranajes (AE) sobre la línea teórica (T1T2) (^{Rodríguez y Espinosa, 2000}; ^{Rodríguez et al., 2007}) logrando una mejor distribución de tensiones a lo largo del contacto (Fig. 3).

Fig. 3 Distribución de las tensiones antes (izquierda) y después (derecha) de ser corregida la transmisión 

La utilización de un factor de corrección adecuado aumenta la resistencia del flanco del diente logrando una mejor distribución de las tensiones de contacto sobre el mismo. Mientras que la elección de valores incorrectos de dicho factor, trae consigo efectos indeseables en la geometría de la transmisión que lejos de aumentar su resistencia la disminuyen, por lo que los límites del factor de corrección están condicionados fundamentalmente por:

Presencia de socavado (límite inferior): El socavado ocurre en engranajes con número de dientes relativamente pequeños, o engranajes que se corrigen con corrección negativa, su límite está determinado por la siguiente ecuación:

Donde:

Z	Número de dientes
h a *	Factor de altura del diente
x	Coeficiente de corrección
m	Módulo del engranaje
α	Ángulo de presión

De donde se deduce el primer límite para la corrección despejando el factor de corrección obteniendo el factor límite para el cual no exista socavado:

() 2

Presencia de aguzado del diente en su punta. (Límite superior): Un criterio aceptado por las normas y algunos autores es que el espesor del diente en su cabeza (S _a ), debe ser superior que 0,20 (^{DIN, 1964}; ^{IS 3756, 2002}; ^{ISO, 1982}) y hasta 0,30 (^{Rockwen, 2001}) veces el valor del módulo, o sea que:

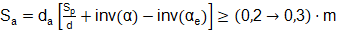𝑆 𝑝 =0,5∙𝜋∙𝑚 +2∙𝑚∙ tan 𝛼 𝑑 𝑎 =𝑚∙ 𝑍+2∙ ℎ 𝑎 ∗ +𝑥 𝑑=𝑚∙𝑍 𝑑 𝑏 =𝑑∙ cos 𝛼 𝛼 𝑒 = cos −1 𝑑 𝑏 𝑑 𝑎 inv 𝛼 = tan 𝛼 −𝛼 inv 𝛼 𝑒 = tan 𝛼 𝑒 − 𝛼 𝑒 () 3

Factor de recubrimiento: Por observaciones experimentales, las normas (^{AGMA, 2004}) sugieren el diseño de engranajes que tengan como mínimo una relación de contacto ε = 1,2. En casos donde se dan correcciones angulares positivas o correcciones de altura corrigiendo positivamente el piñón y negativamente la corona, la relación de contacto tiende a disminuir, por lo que hay que garantizar que no se pierda el contacto ininterrumpido de los dientes, para esto es importante mantener la siguiente relación:

()4

Donde:

Las correcciones angulares negativas o de altura corrigiendo negativamente el piñón y positivamente la corona tienen muy poca aplicación práctica; no obstante, en estos casos no hay que chequear el coeficiente de recubrimiento, pues el mismo aumenta.

2.2. Modelo de optimización

Para la determinación de los factores de corrección para mínimas tensiones de contacto que cumplan con las restricciones geométricas antes preestablecidas (ecuaciones 2, 3, 4) se puede formular el problema como un problema de optimización mono-objetivo con restricciones de la siguiente forma:

Determinar X ₁ tal que:

Minimice 𝜎 𝐻 =𝑓( 𝑥 1 , 𝑥 𝑠 )

Sujeto a:

X_s = X ₁ + X ₂ ; corrección sumaria, asumida como constante de diseño

X_min ≤ X₁ ≤ X_máx

Donde:

X_min y X_máx garanticen las restricciones geométricas (ecuaciones 2 y 3) del dentado en cada engranaje, a la vez que la transmisión garantice un factor de recubrimiento mayor igual a 1,2 (ecuación 4).

En el modelo planteado se define una función objetivo, las tensiones de contacto ( 𝜎 𝐻 ), que pueden ser evaluadas por cualquiera de las normas de diseño existentes (ISO, AGMA, DIN, GOST, etc.), la cual describe una función con un solo mínimo global 𝜎 𝐻𝑚𝑖𝑛 (Fig. 3). Dicha función objetivo se plantea en función de la corrección del piñón (X₁) y la corrección sumaria ( 𝜎 𝐻 =𝑓( 𝑥 1 , 𝑥 𝑠 )), con el objetivo de no afectar la distancia entre centros de la transmisión haciendo el modelo válido tanto para corrección de altura ( 𝑥 𝑠 =0 como para corrección angular ( 𝑥 𝑠 ≠0). El valor del factor de corrección para la corona ( 𝑥 2 ) es determinado en cada caso como 𝑥 2 = 𝑥 𝑠 − 𝑥 1 .

Siendo 𝑥 𝑠 una constante de diseño, para cada par engranado, y el factor de corrección del piñón ( 𝑥 1 ) variable en el rango establecido en el modelo (𝑥 min − 𝑥 máx ) que cumpla con las restricciones de las ecuaciones (2, 3 y 4); la solución del problema planteado puede ser determinada por cualquier método de optimización mono-objetivo con restricciones, los cuales fueron utilizados con este fin, a la vez que se desarrolló e implementó (^{Donéstevez, 2014}) una solución numérica, presentada en la (Fig. 4), basada en el conocido método de bisección, descrito a continuación.

2.3. Método de solución numérica del problema de optimización

En el método de solución desarrollado para este trabajo (Fig. 4) requiere de una precisión para su convergencia, pues el mismo está basado en el método numérico de bisección. La precisión establecida para los algoritmos presentados anteriormente es de cinco valores decimales (10^-5), la cual en situaciones prácticas podría estar condicionada por la precisión de la máquina herramienta donde se construirán dichos engranajes, en conjunto con las especificaciones del diseño.

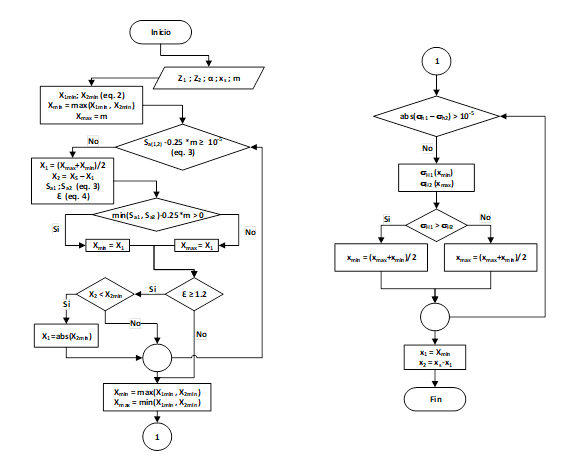
Fig. 4 Diagrama de bloque para la determinación de los factores de corrección máximo para mínimas tensiones de contacto 

El algoritmo consta de dos ciclos de convergencia, el primero con el objetivo de buscar los factores de correcciones límites que cumplan con las restricciones geométricas planteadas en las ecuaciones 2-4 que funciona de la siguiente forma:

• Determina un factor de corrección que garantice que no hay socavado en ninguno de los engranajes (máx. (X_1min, X_2min)), obtenidos por la ecuación 2, y es establecido como el factor de corrección mínimo.

• El factor de corrección máximo se establece con un valor arbitrario igual al módulo de la transmisión.

• El ciclo comienza tomando como punto de parada del ciclo el criterio de la ecuación 3, en busca de la corrección máxima que garantice que no hay afilamiento del diente en ninguno de los engranajes. Los valores máximo y mínimo de corrección van siendo evaluados según las restricciones de la ecuación 3 cambiando su valor utilizando el punto medio entre la corrección máxima y mínima en cada iteración (bisección).

• Antes de salir de cada iteración se evalúa el factor de recubrimiento, el cual de ser incumplida esta restricción el ciclo se detiene automáticamente.

El segundo ciclo comienza con las correcciones máximas y mínimas obtenidas previamente, utilizadas como factor de corrección para el piñón (X₁) y el factor de corrección de la corona es determinado según la corrección sumaria (X2=Xs-X1); con estos valores se evalúan las tensiones de contacto, por cualquiera de las normas o métodos existentes, para los valores máximo y mínimo del factor de corrección, luego se comparan dichas tensiones para saber hacía cuál de los extremos del factor de corrección se encuentran las tensiones mínimas, y se aproxima su encuentro utilizando nuevamente bisección hasta alcanzar la precisión prescrita al principio.

RESULTADOS Y DISCUSIÓN

La validación del método propuesto se hace partir de la determinación de los factores de corrección obtenidos por el modelo propuesto comparados por los recomendados por el programa de diseño KISSSoft-v2014, evaluadas para las normas (^{AGMA, 2004}; ^{ISO 6336-2, 2006}) implementadas por los autores. El análisis se hace a partir de una muestra de 12 pares de engranajes, donde:

• Número de dientes piñón (Z₁): 17 - 40

• Relación de transmisión (u): 1 < u < 4

• Módulo del engranaje (m): 1

• Factor de altura del diente (h_a*): 1

• Ángulo de presión: (α) 20°

La (Fig. 5) muestra comparativamente los tiempos de convergencia de los distintos métodos evaluados para los 12 pares engranados, calculados utilizando las tensiones de contacto según la norma (^{AGMA, 2004}). La principal diferencia en el resultado del método numérico presentado y otros algoritmos de optimización conocidos está dada por el tiempo de convergencia de los mismos.

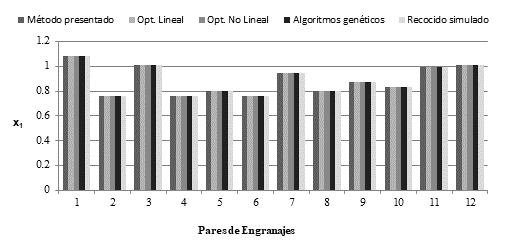
La (Fig. 6) ilustra los resultados obtenidos por cada uno de los algoritmos de optimización con los cuales se determinó el factor de corrección máxima para mínimas tensiones de contacto, dándole solución al objetivo planteado. Los valores del factor de corrección determinados por todos los métodos evaluados arrojan los mismos resultados.

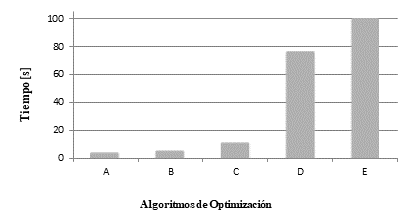
Fig. 5 Comparación del tiempo de convergencia de los diferentes algoritmos de optimización con el método presentado. A) Método presentado. B) Optimización Lineal, C) Optimización no Lineal, D) Algoritmos Genéticos, E) Recocido Simulado 

Fig 6 Comparación del factor de corrección determinado por cada uno de los algoritmos 

La obtención de valores similares del factor de corrección óptimo para mínimas tensiones de contacto por todos los algoritmos (Fig. 6) garantiza la validez del planteamiento del problema como problema de optimización haciéndolo fiable para la determinación de un valor del factor de corrección que minimiza las tensiones de contacto. Por otra parte, también se valida el algoritmo presentado (Fig. 4), como un algoritmo válido para la solución del problema planteado, lo cual simplifica la implementación de esta solución, siendo más sencilla que cualquiera de los algoritmos clásicos de optimización.

La tabla 1 muestra un análisis comparativo de los resultados obtenidos por el método de optimización planteado y los valores del factor de corrección, para atenuar la falla por picadura, recomendados por el programa comercial KISSSoft-v2014 para las normas de diseño (^{AGMA, 2004}; ^{ISO 6336-2, 2006}).

La comparación de los resultados obtenidos con uno de los programas comerciales de diseño más reconocidos (KISSSoft-v2014) valida el planteamiento y solución del problema de la obtención del factor de corrección óptimo para menores tensiones de contacto como un problema de optimización con restricciones geométricas. Las mayores diferencias obtenidas, pueden estar dadas por diferencias en la implementación de las normas por los autores. Teniendo en cuenta que el porciento de error nunca supera el 10% se recomienda ésta metodología.

Tabla 1 Comparación de los valores del factor de corrección obtenidos por el método presentado y los recomendados por el programa de diseño KISSSoft-v2014, para diferentes normas 

Par	Optimización		KISSSoft		% Error
	ISO	AGMA	ISO	AGMA	ISO	AGMA
1	0,2869	1,0798	0,2800	1,0090	2,,48	7,02
2	0,4061	0,7589	0,4090	0,8010	0,72	5,25
3	0,3022	1,0140	0,3050	1,0090	0,92	0,49
4	0,2639	0,7617	0,2620	0,7920	0,72	3,82
5	0,3870	0,7982	0,3880	0,8420	0,26	5,20
6	0,4061	0,7589	0,4090	0,8010	0,72	5,25
7	0,3259	0,9454	0,3280	0,9930	0,63	4,80
8	0,3870	0,7982	0,3880	0,8420	0,26	5,20
9	0,3538	0,8736	0,3500	0,9190	1,10	4,94
10	0,3696	0,8364	0,3970	0,8440	6,89	0,90
11	0,9505	0,9983	0,9600	0,9600	0,99	3,99
12	0,3022	1,0140	0,3050	1,0090	0,92	0,49

En las tabla 2 y tabla 3 se presenta una comparación entre el valor del factor de corrección máxima para mínimas tensiones de contacto expresado por la ecuación 1 y el mismo determinado por los métodos del presente trabajo, mediante un análisis de estos resultados se puede determinar que:

• En 9 de los 12 casos presentados, el factor de corrección calculado por la ecuación 1 supera el máximo valor geométrico de corrección que se puede dar (casos marcados con *), por lo que de utilizar la ecuación 1, sin chequear las restricciones (ecuaciones 2, 3 y 4) traería defectos en el dentado (afilamiento).

• El factor de corrección determinado por el modelo presentado, determina en cada uno de los casos, geométricamente posibles, tensiones menores que los determinados por la ecuación 1, tanto para la norma ISO como AGMA, aunque las diferencias no son muy notables. Lo que hace del punto anterior el principal fundamento para el uso del modelo presentado en este trabajo sobre el ya defendido en la ecuación 1.

Tabla 2 Tensiones de contacto según norma AGMA evaluada para factores de corrección límite, con X_s = 0, según método presentado y la ecuación 1 

Par	X min	X máx	X 1 +	X 1	σ H (x 1 )	σ H (x 1 +)	σ H (x 1 ) - σ H (x 1 +)
1	-0,520	1,079	1,468*	1,079	1295,4	1273,8	21,6
2	0,005	0,758	1,005*	0,758	2097,8	2054,8	42,9
3	-0,403	1,013	1,518*	1,013	1393,9	1358,0	35,9
4	-0,637	1,143	0,458	0,761	1401,3	1408,1	-6,8
5	-0,052	0,798	1,952*	0,798	1815,4	1637,3	178,1
6	0,005	0,758	1,156*	0,758	2060,5	1989,8	70,7
7	-0,286	0,945	0,648	0,945	1708,1	1723,7	-15,6
8	-0,052	0,798	1,506*	0,798	1873,6	1763,8	109,8
9	-0,169	0,873	1,198*	0,873	1729,6	1693,6	36,0
10	-0,111	0,836	1,060*	0,836	1853,7	1825,7	27,9
11	-1,04711	1,34883	0,69917	0,99831	1083,438	1086,537	-3,1
12	-0,403	1,013	1,127*	1,013	1454,6	1447,6	6,9

+ Representa factor de corrección obtenido por la ecuación 1.

* Casos para los cuales el factor de corrección obtenido por la ecuación 1, está fuera del rango de las restricciones geométricas planteadas por las ecuaciones 2-4.

Tabla 3 Tensiones de contacto según norma ISO evaluada para factores de corrección límite, con X_s = 0, según método presentado y la ecuación 1 

Par	X min	X máx	X 1 +	X 1	σ H (x 1 )	σ H (x 1 +)	σ H (x 1 ) - σ H (x 1 +)
1	-0,520	1,079	1,468*	0,286	1241,8	1308,9	-67,1
2	0,005	0,758	1,005*	0,406	2292,4	2309,0	-16,5
3	-0,403	1,013	1,518*	0,302	1378,1	1431,3	-53,1
4	-0,637	1,143	0,458	0,263	1235,5	1241,4	-5,9
5	-0,052	0,798	1,9527*	0,386	2006,9	2013,4	-6,4
6	0,005	0,758	1,156*	0,406	2267,0	2286,8	-19,7
7	-0,286	0,945	0,648	0,325	1665,5	1677,1	-11,6
8	-0,052	0,798	1,506*	0,386	2048,1	2047,2	0,8
9	-0,169	0,873	1,198*	0,353	1803,9	1839,1	-35,2
10	-0,111	0,836	1,060*	0,369	1955,9	1981,8	-25,9
11	-1,047	1,348	0,699	0,950	944,2	964,0	-19,7
12	-0,403	1,013	1,127*	0,302	1415,3	1456,0	-40,6

+ Representa factor de corrección obtenido por la ecuación 1.

*Casos para los cuales el factor de corrección obtenido por la ecuación 1, está fuera del rango de las restricciones geométricas planteadas por las ecuaciones 2-4.

CONCLUSIONES

1. La obtención de un valor del factor de corrección, puede ser planteada y resuelta como un problema de optimización con restricciones; considerando los límites del factor de corrección, cumpliendo las restricciones geométricas para evitar el socavado y aguzado del dentado, y con un coeficiente de recubrimiento mayor o igual 1,2.

2. El modelo presentado determina el valor del factor de corrección para mínimas tensiones de contacto, considerando las restricciones geométricas de la transmisión, para determinar las tensiones de contacto.

3. El método numérico presentado en el trabajo para la solución del modelo obtiene los mismos resultados que los métodos clásicos de optimización, validando su uso en la solución del problema.

4. Las diferencias del factor de corrección determinado por el modelo presentado, en comparación con los valores recomendados por el programa de diseño de elementos de máquina KISSSoft-v2014, no difieren en más de un 10%, lo cual avala su validez para su uso futuro. Estas diferencias son significativamente mayores en las normas AGMA lo cual sugiere una revisión en la implementación de las mismas por los autores.

REFERENCIAS

AGMA., ANSI/AGMA 2101-D04. Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth., United States of America. 2004, pp. 07-38.

Budynas, R.G., & Nisbett, J.K., Diseño en Ingeniería Mecánica de shigley., McGraw-Hill/Interamericana de México, Trans, 9na edición en Español, 2012, pp. 673-775.

Caballero, S.S., Cantó, M.Á.S., Rasero, M.Á.P., & Ferrando, R.P., Optimización de transmisiones de engranajes mediante algoritmos evolutivos., Ciencias, Vol. 7, No. 03, 2013, pp. 1-17.

DIN., DIN 3992:1964, Addendum modification of external spur and helical gears., 1964, pp. 02-09.

Donéstevez, E.M.F., Modelo para el cálculo del factor de corrección que determine las tensiones mínimas de contacto en los dientes de engranajes cilíndricos de dientes rectos metálicos con contacto exterior engranados., Tesis presentada en opción al Grado Científico de Master en Ciencias Técnicas, Especialidad Ingeniería Mecánica en la Universidad Central “Marta Abreu” de Las Villas, Cuba, 2014.

Estrems, M., Modelo de cálculo a presión superficial de engranajes cilíndricos de perfil de evolvente., Tesis presentada en opción al Grado Científico de Doctor en Ingeniería Industrial, Universidad de Murcia, España, 1998. Disponible en: http://repositorio.bib.upct.es:8080/dspace/bitstream/10317/2724/1/mcp.pdf

Gunay, D., Ozer, H., & Aydemir, A., The effects of addendum modification coefficient on tooth stresses of spur gear., Mathematical & Computational Applications, Vol. 1, No. 01, 1996, pp. 36-43.

IS 3756:2002., Method for gear correction - Addendum modification for external cylindrical gears with parallel axes., India, 2002, pp. 4-14.

ISO., Technical Report, ISO/TR 4467, Addendum modification of the teeth of cylindrical gears for speed reducing and speed increasing gearpairs.,1982 pp. 02-12.

ISO 6336-2., Calculation of load capacity of spur and helical gears., Part 2: Calculation of surface durability (pitting)., Switzerland, 2006, pp. 10-33.

Karadere, G., & Yilmaz, I., Investigation of the Effects of Profile Shift in Helical Gear Mechanisms with Analytical and Numerical Methods., World Journal of Mechanics, Vol. 8, No. 01, 2018, pp. 200-209.

Korta, J.A., & Mundo, D., Multi-objective micro-geometry optimization of gear tooth supported by response surface methodology., Mechanism and Machine Theory, Vol. 109, No. 109, 2017, pp. 278-295.

Lemos, E.M., & Delgado, L.M., Razón de contacto en engranajes cilíndricos rectos con socavado., Ingeniería Mecánica, Vol. 3, No. 01, 2007, pp. 19-24.

Machado, Á.S., Consideraciones acerca del diseño de los engranajes cilíndricos de dientes rectos, aplicables a su recuperación., Tesis presentada en opción al Grado Científico de Doctor en Ciencias Técnicas, Especialidad Ingeniería Mecánica, Universidad Central “Marta Abreu”de Las Villas, Facultad de Ingeniería Mecánica, Santa Clara, Cuba, 2000.

Marimuthu, P., & Muthuveerappan, G., Optimum Profile Shift Estimation on Direct Design Asymmetric Normal and High Contact Ratio Spur Gears Based on Load Sharing., Procedia Engineering, Vol. 86, No. 03, 2014, pp. 709-717.

Merritt, H.E., Gear Engineering., Editorial John Wiley & Sons Inc., 1975, pp. 48-53.

Milera, D., Lončarb, A., Žeželja, D., & Domitrana, Z., Influence of profile shift on the spur gear pair optimization., Mechanism and Machine Theory, Vol. 117, No. 24-35, 2017, pp.189-197.

Milojevi´, M., Optimization of Transverse Load Factor of Helical and Spur Gears Using Genetic Algorithm., Applied Mathematics & Information Sciences, Vol. 7, No. 4, 2013, pp. 1323-1331.

Rey, G.G., Cálculo de engranajes cilídricos., Tesis presentada en opción al Grado Científico de Master en Diseño Mecánico, CUJAE, La Habana, Cuba, 2001.

Rockwen, P.D., Profile Shift in External Parallel-Axis Cylindrical Involute Gears., Gear Technology, Vol. 3, No. 4, 2001, pp. 18-25.

Rodríguez, J.L.M., & Espinosa, R.G., Correcciones en las Transmisiones por Engranajes Cilíndricos de Dientes Rectos., Monografía, Universidad Central “Marta Abreu”de Las Villas, Facultad de Ingeniería Mecánica, Santa Clara, Villa Clara, Cuba., 2000, pp. 01-31.

Rodríguez, J.L.M., Espinosa, R.G., Quiñones Cherta, A., & Curbelo Hidalgo, L., Corrección de altura para máxima resistencia a la fractura en engranajes cilíndricos de dientes rectos bajo diferentes coeficientes de fricción., Paper presented at the 8º Congresso Iberoamericano de Ingeniería Mecánica, Cusco, Perú, 2007.

Recibido: 15 de Julio de 2019; Revisado: 02 de Octubre de 2019; Aprobado: 09 de Diciembre de 2019

^*Autor para la correspondencia: Ángel S. Machado, Email:[e-mail]

Los autores declaran que no existe conflicto de interés.

M.Sc. Eduardo M. Fírvida Donéstevez. Escribió el artículo y desarrolló la investigación.

Dr.C. Ángel S. Machado Rodríguez. Participó en la escritura y revisión del artículo. Colaboró en la búsqueda de la información y el análisis de los resultados. Formateó el artículo y lo envió a la revista.

Dr.C. Jorge L. Moya Rodríguez. Participó en la escritura del artículo y revisión del artículo, así como en el análisis de los resultados.