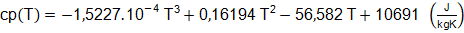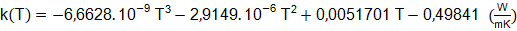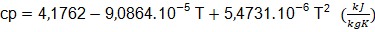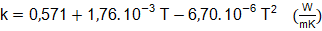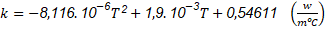Artículo Original

ESTIMACIÓN DE PROPIEDADES TERMOFÍSICAS DE LA CERVEZA EMBOTELLADA, BAJO CONDICIONES DE PASTEURIZACIÓN

THERMO PHYSICAL PROPERTIES ESTIMATION FOR UNDER PASTEURIZATION CONDITIONS BOTTLED BEER

0000-0003-1858-705XMisdelki Pérez Colas^{1  *}  , 0000-0002-9280-510XMartha Faustina Nápoles García¹  , 0000-0003-3755-3787María de Lourdes de la Cruz Aragoneses¹ 

¹Facultad de Ciencias Aplicadas. Universidad Ignacio Agramonte Loynaz, Camagüey. Carretera Circunvalación Norte km 5½. Camagüey, Cuba.

RESUMEN

Introducción:

En la simulación del proceso de pasteurización de la cerveza envasada, se requiere del uso de los balances de continuidad, energía y cantidad de movimiento, y estos modelos matemáticos en estado no estacionario, necesitan los valores de la densidad, la viscosidad, la capacidad calorífica y la conductividad térmica. Se ha encontrado que algunos investigadores utilizan modelos de las propiedades termofísicas del agua, para estimar las de la cerveza, sin realizar ningún análisis que demuestre que esto sea confiable.

Objetivo:

Validar el uso de modelos matemáticos para la estimación de las propiedades termofísicas del agua, aplicando técnicas estadísticas, que permitan compararlos con modelos, datos y valores reportados por diferentes autores, para emplearlos posteriormente en la simulación del proceso de pasteurización de la cerveza embotellada.

Materiales y Métodos:

Para la validación de los modelos de las propiedades del agua se emplearon el análisis de regresión y las pruebas de hipótesis, a partir de las que se realizaron comparaciones entre los modelos y valores reportados.

Resultados y Discusión:

Al comparar las medias entre las propiedades obtenidas por los modelos para el agua con las obtenidas por otros autores, se obtienen valores de la probabilidad mayores que 0,05, por lo que no se rechaza la hipótesis nula, Ho. Mostrándose que no existen diferencias estadísticamente significativas entre los valores analizados.

Conclusiones:

Se propone utilizar los modelos correspondientes al agua en la estimación de las propiedades termofísicas de la cerveza, en el rango de temperatura del proceso de pasteurización, en estudios futuros de simulación.

Palabras-clave: capacidad calorífica; conductividad térmica; densidad; pasteurización; viscosidad

ABSTRACT

Introduction:

In bottled beer pasteurization process simulation, continuity, energy and momentum balances use is required, and these mathematical models in non-steady state require of density, viscosity, heat capacity and thermal conductivity values. Some researchers have used thermo physical water properties to estimate those of beer, without performing any analysis that shows that this is reliable.

Objective:

To validate mathematical models use to estimate the thermo physical water properties, applying statistical techniques that allow them to be compared with models, data and values ​​reported by different authors, to be used later in bottled beer pasteurization process simulation.

Materials and methods:

For water properties models validation, regression analysis and hypothesis tests were used, from which comparisons between models and reported values were made.

Results and Discussion:

When comparing means between obtained by models water properties with those obtained by other authors, probability values greater than 0.05 are obtained, so null hypothesis, Ho, is not rejected. So there are no statistically significant differences between analyzed values.

Conclusions:

It is proposed to use corresponding to water models in beer thermo physical properties estimation, in pasteurization process temperature range, in future simulation studies.

Key words: heat capacity; Thermal conductivity; density; pasteurization; viscosity

INTRODUCCIÓN

En los estudios de simulación realizados para el proceso de pasteurización de la cerveza envasada en botellas de vidrio, se ha considerado el recipiente como la célula del proceso, debido a que en el interior de este se desarrolla un proceso en estado no estacionario. Teniendo en cuenta que es en el interior de la botella donde sucede el calentamiento, pasteurización y enfriamiento de la cerveza, los softwares profesionales aplicados para la simulación han utilizado modelos multifísicos de transferencia de calor y flujo de fluidos en estado no estacionario a un nivel microscópico. Estos tienen estructura matemática de ecuaciones diferenciales parciales que han requerido la estimación de las propiedades termofísicas de la cerveza, entre ellas la densidad, la viscosidad, la capacidad calorífica y la conductividad térmica (^{Viera y col., 1988}), (^{Patiño y col., 2001}), (^{Patiño y col., 2005}), ^{Hoffman (2006}), (^{Augusto et al., 2010}), (^{Nápoles y col., 2020}).

Se pueden aplicar diferentes métodos para la estimación de propiedades termofísicas en los líquidos. La densidad, ρ, puede ser obtenida con el uso de un hidrómetro, un densímetro, un picnómetro, o aplicando el método de pesadas hidrostáticas (^{Rosabal y Garcell, 2006}), ^{Hernández (2014}), ^{Martínez (2015}). Para cuantificar la viscosidad dinámica, μ, se utilizan los viscosímetros y estos varían según la clasificación de los fluidos (newtonianos o no newtonianos). Los más conocidos son los de tubo capilar, los rotacionales y el Hoppler o de bola. Existen además modelos matemáticos reportados en la literatura (^{Bird, y col., 1992}), (Rosabal y Garcell, 2006), (^{Martínez y Benítez, 2008}), ^{Galán (2018}). En el caso de la conductividad térmica, k, se hace difícil su determinación experimental ^{Kern (1999}), sin embargo (^{Martínez y Benítez, 2009}) ofrecen un compendio de métodos generalizados de estimación que permite obtenerla por métodos empíricos a partir de otros datos de la sustancia en cuestión o de las sustancias que componen la mezcla. (^{Abdulagatov y Magomedov, 2003}) y ^{Aparicio (2009}) han empleado en sus estudios la sonda del hilo caliente. La capacidad calorífica, cp, es posible predecirla para un alimento conociendo su composición. ^{Zegarra (2014}), plantea una ecuación para obtenerla dependiendo de la cantidad de agua y otros componentes. Se puede medir de manera directa, empleando sistemas calorimétricos o mediante métodos indirectos como la calorimetría diferencial de barrido según Aparicio (2009).

Existen modelos para determinar propiedades termofísicas para los alimentos. ^{Orrego (2003}), plantea modelos para la densidad, la capacidad calorífica y la conductividad térmica de alimentos líquidos, en función de la temperatura, en un rango entre 0 a 60 ^oC, no ofreciendo un modelo para la viscosidad. ^{Hayes (1987}) y ^{Earle (1988}) también ofrecen modelos en función de la composición del alimento.

Dado el gran contenido de agua en la cerveza, en la literatura se encuentran algunas de sus propiedades en función de este componente. ^{Hayes (1987}) y ^{Suárez (2013}) reportan la densidad con un valor de 1 000 kg/m³ y la viscosidad de 0,0013 Ns/m², ambas a 0 ºC. En el caso de la conductividad térmica se plantean valores entre 0,52 y 0,64 W/mºC, y la capacidad calorífica de 4,19 kJ/kgºC ambas para un 92% de agua. Esta última propiedad también se presenta por ^{Earle (1988}) bajo la misma condición.

En la simulación de la pasteurización cervecera se utilizan las propiedades termofísicas. ^{Patiño y col., (2001}) presentaron un análisis térmico y flujo-dinámico de la cerveza en el proceso de pasteurización en un túnel utilizando la simulación numérica, mostrando una tabla con modelos para las propiedades termofísicas. Utilizando el mismo procedimiento de su investigación anterior ^{Patiño y col., (2005)} analizaron, el efecto que produce la presión dinámica ejercida por el dióxido de carbono sobre las características de flujo y temperatura en la superficie superior de la cerveza, planteando valores de las propiedades termofísicas de la cerveza y el CO₂ que fueron empleadas, para el rango de temperatura bajo estudio. En ninguna de estas investigaciones se especifica la procedencia de los modelos y datos de las propiedades expuestas.

^{Hoffman, (2006}) modeló la pasteurización de cerveza en un pasteurizador de túnel, exhibiendo los modelos y valores de las propiedades esclareciendo que se refieren al agua, pero no se aprecia ningún análisis que demuestre que esto sea confiable. También (^{Dilay et al., 2006}) simularon la pasteurización de cerveza en el túnel, realizando la optimización de las dimensiones del equipo utilizando un modelo macroscópico, con valores promedio de las propiedades físicas de interés para los fluidos.

^{Girotti (2009}) tuvo como objetivo investigar los fenómenos de transferencia de calor que ocurren en la pasteurización de la cerveza embotellada. ^{Augusto et al., (2010}) basaron su estudio en la simulación de un proceso similar, buscando analizar la influencia de la posición del recipiente, en este caso en latas. Aunque ambos autores no emiten criterios sobre la procedencia de las propiedades de los fluidos, se observa que están presentes en los modelos que se utilizaron y se trata la cerveza como agua.

^{Bhuvaneswari y Anandharamakrishnan, (2014}) en un estudio semejante a los anteriores, utilizaron los modelos estimativos para la capacidad calorífica y la conductividad térmica de la cerveza y muestran una comparación gráfica entre estas propiedades con las correspondientes al agua, planteando que esta información se ha obtenido de otra referencia.

Unido a lo anterior, existe el hecho de que no todos los alimentos tienen definido valores de las propiedades termofísicas en el rango de temperatura de trabajo en los procesos, y tomando en cuenta que en la simulación las propiedades cambian con la temperatura y con el tiempo, como ya se ha planteado, este aspecto de la estimación de las propiedades resulta un punto crucial durante el desarrollo de la simulación, siendo necesario analizarlo profundamente como plantean ^{Vargas y col., (2020}).

Teniendo en cuenta que los modelos utilizados por ^{Hoffman (2006}) para la estimación de las propiedades termofísicas, no están fundamentados estadísticamente y que no se ha visto claridad en la procedencia de las propiedades utilizadas por los demás investigadores que han tratado la simulación del proceso de pasteurización cervecera en el interior de la botella. Se considera que, utilizando técnicas estadísticas para comparar los modelos empleados por Hoffman (2006) con los modelos planteados por ^{Orrego (2003}) y por ^{Bhuvaneswari y Anandharamakrishnan, (2014}), así como con los valores de las propiedades reportados por ^{Hayes (1987}), ^{Earle (1988}) y ^{Suárez (2013}), puede justificarse el uso de los modelos existentes para el agua en la estimación de las propiedades de la cerveza. Considerando que Orrego (2003) no reporta modelos para la determinación de la viscosidad, en este estudio puede emplearse uno de los métodos de determinación experimental de la viscosidad, para obtener un modelo que permita la comparación con los valores que se determinen a partir de los modelos utilizados por Hoffman (2006).

Por lo anterior el objetivo de esta investigación es, validar el uso de modelos matemáticos para la estimación de las propiedades termofísicas del agua, aplicando técnicas estadísticas, que permitan compararlos con modelos, datos y valores reportados por diferentes autores, para emplearlos posteriormente en la simulación del proceso de pasteurización de la cerveza embotellada.

MATERIALES Y MÉTODOS

2.1 Modelos matemáticos y valores puntuales de estimación de las propiedades termofísicas.

^{Hoffman (2006}) presenta modelos matemáticos para el agua, de la densidad, la viscosidad, la capacidad calorífica y la conductividad térmica. ^{Orrego (2003}) plantea modelos para alimentos que contienen agua, de la densidad, la capacidad calorífica y la conductividad térmica. ^{Bhuvaneswari y Anandharamakrishnan, (2014}) muestran modelos para la cerveza, de la capacidad calorífica y la conductividad térmica.

^{Hayes (1987}) ofrece valores puntuales de las cuatro propiedades que se analizan. ^{Earle (1988}) presenta un valor para la capacidad calorífica y ^{Suárez (2013}) un valor para la densidad, en ambos casos semejantes a los que reporta Hayes (1987).

Se obtuvieron valores de las propiedades a partir de los modelos reportados en el rango de temperatura de interés, desde 5 a 60 ^oC que corresponde con las condiciones de trabajo del pasteurizador.

En el caso de la viscosidad, se realizaron determinaciones experimentales de la misma, tomando una muestra de cerveza de denominación 10^o 70/30, para poder ajustar un modelo de estimación, ya que ^{Orrego (2003}) no brinda modelo para dicha propiedad.

Los modelos de estimación reportados son los siguientes (Ecuaciones 1, 2, 3, 4, 5, 6, 7, 8 y 9):

Utilizados por ^{Hoffman (2006})

Densidad

(1)

Capacidad calorífica

(2)

Conductividad térmica

(3)

Viscosidad dinámica

(4)

La temperatura T debe sustituirse en K.

Utilizados por ^{Orrego (2003}). Este autor plantea correlaciones de los componentes de los alimentos en general como función de la temperatura, reportándose los siguientes modelos donde la temperatura se sustituye en ºC.

Densidad

(5)

Capacidad calorífica

(6)

Conductividad térmica

(7)

Viscosidad

El autor no reporta modelo de estimación

Utilizados por ^{Bhuvaneswari y Anandharamakrishnan, (2014}). Reportan que estos modelos son para la cerveza

Capacidad calorífica

(8)

Conductividad térmica

(9)

2.2 Métodos para la validación de los modelos matemáticos de estimación de las propiedades termofísicas.

Para la validación de los modelos de estimación de propiedades termofísicas, es necesaria la aplicación de técnicas estadísticas que permitan llegar a resultados que aumenten la confiabilidad del uso de los modelos escogidos. Para el procesamiento de los datos se utilizan softwares especializados, como el Statgraphics, que ayuda a realizar tanto la estadística descriptiva como la inferencial (^{Walpole y col., 1998}), ^{Wong (2010}), ^{Montgomery (2017}), ^{Posada (2016}).

Para llevar a cabo la validación se trabajó con los modelos de ^{Hoffman (2006}), para las cuatro propiedades y con los de ^{Orrego (2003}) para la densidad, la capacidad calorífica y la conductividad térmica, estimándose los valores de las propiedades en el rango de temperatura de 5 a 60 ^oC, utilizando una hoja de cálculo en Microsoft Excel 2010. Los valores estimados se compararon realizando una prueba de hipótesis para medias, empleando el software Statgraphics.

Se realizó también una comparación con el valor de las cuatro propiedades obtenidas con los modelos de ^{Hoffman (2006}) y con los valores únicos de las cuatro propiedades reportados por ^{Hayes (1987}) y ^{Earle (1988}) para la cerveza.

Como ^{Bhuvaneswari y Anandharamakrishnan, (2014}), plantean que utilizan modelos para la capacidad calorífica y la conductividad térmica de la cerveza, los resultados calculados para estas propiedades con dichos modelos, se comparan con los valores puntuales reportados por ^{Hayes (1987}) y ^{Earle (1988}) para cerveza, mediante una prueba de hipótesis.

Debido a que no se ha encontrado un modelo de estimación para la viscosidad de la cerveza en la literatura consultada, se procedió a determinarla experimentalmente para el rango de temperatura de 17 a 59,5 ^oC, utilizando un viscosímetro Hoppler, con el fin de obtener valores para ajustar un modelo matemático.

Con los valores de viscosidad obtenidos se ajustó un modelo por regresión μ=f (T), con el que se estimaron valores de viscosidad y fueron comparados con los de ^{Hoffman (2006}) utilizando una prueba de hipótesis.

En la Tabla 1 se presenta un resumen de los modelos matemáticos y los valores de propiedades termofísicas que fueron utilizados en la comparación.

Tabla 1 Modelos y valores de propiedades termofísicas que fueron comparados 

Referencia	Propiedades termofísicas	Comparada con	Propiedades termofísicas
Hoffman (2006)	Modelos matemáticos de la densidad, conductividad térmica y capacidad calorífica, para el agua	Orrego (2003)	Modelos matemáticos de la densidad, conductividad térmica y capacidad calorífica, para alimentos que contienen agua
Hoffman (2006)	Modelo matemático de la viscosidad, para el agua	Resultado de la determinación experimental de este estudio	Modelo obtenido por regresión, para la viscosidad
Hoffman (2006)	Modelos matemáticos de la densidad, viscosidad, conductividad térmica y capacidad calorífica, para el agua	Hayes (1987) Earle (1988) y Suárez (2013)	Valores puntuales para la densidad, viscosidad, conductividad térmica y capacidad calorífica de la cerveza
Bhuvaneswari y Anandharamakrishnan, (2014)	Modelos matemáticos de la conductividad térmica y la capacidad calorífica, de la cerveza	Hayes (1987) y Earle (1988)	Valores puntuales para la conductividad térmica y capacidad calorífica de la cerveza

RESULTADOS Y DISCUSIÓN

3.1 Análisis estadístico del modelo obtenido

Para analizar el comportamiento de la viscosidad a diferentes temperaturas se midió esta para cinco valores de temperatura: 17, 30,5, 41, 58,5 y 59,5 ^oC, las que fueron posible ajustar según las condiciones del termostato utilizado, acoplado al viscosímetro dentro del intervalo de temperatura bajo estudio. Con los valores de viscosidad determinados a partir del experimento se realizó el ajuste de un polinomio, utilizando el software Statgraphics, a través de un análisis de regresión, cuyos resultados se muestran en la Tabla 2.

Tabla 2 Variables y resultados para el ajuste del polinomio 

Variable	T (ºC)	17	30,5	41	58,5	59,5
Resultados	μ (Pa.s *10³)	1,0465	0,8385	0,7765	0,7085	0,6925

Realizando el análisis de regresión polinomial, tomando como la variable dependiente a la viscosidad y la independiente a la temperatura, se obtiene la ecuación (10):

(10)

En el modelo descrito anteriormente la viscosidad se reporta en Pa.s·10^-3. Su validez se discute a partir de los resultados que aparecen en la Tabla 3.

Tabla 3 Resultados del análisis de los parámetros del modelo obtenido 

Parámetro	Probabilidad
T	0,021
T^2	0,043

Como la probabilidad asociada a los parámetros es menor que 0,05 todos tienen significación en el modelo al 95 % de confianza.

El análisis de varianza también muestra significación del modelo (p=0,0084), el coeficiente de determinación es alto (99,16), lo que muestra la contribución de las variables consideradas T y T², con la viscosidad.

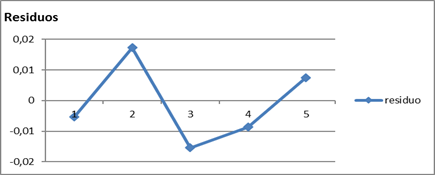
El comportamiento de los residuos, es aleatorio, pues no siguen ningún patrón específico, como se observa en la Fig. 1.

Fig. 1 Comportamiento de los residuos 

El grado del polinomio es adecuado a un 95 % de confianza, pues P para el término de mayor orden (T²) es de 0,0434, el que es menor de 0,05.

De todo lo anterior se concluye que se acepta el modelo obtenido para continuar los estudios, comparando lo estimado por ^{Hoffman (2006}) con los determinados por la ecuación (10) obtenida en la investigación.

3.2 Análisis de la validez de los modelos para las diferentes propiedades

Los resultados de las pruebas de hipótesis realizadas, al comparar los valores de las cuatro propiedades obtenidas por los modelos de ^{Hoffman (2006}), con las obtenidas por los modelos de ^{Orrego (2003}), considerando además el modelo obtenido en la determinación experimental de la viscosidad y con los valores puntuales expuestas en la literatura, se muestran en la Tabla 4.

Tabla 4 Resultados de las pruebas de hipótesis entre ^{Hoffman (2006}) y otros autores 

	Modelos y/o valores analizados
Prueba de hipótesis	ρH - ρO	ρH - ρHayes	kH - kO	kH - kHayes
Probabilidad	0,5347	0,29	0,995	0,11*
Consideración	no se rechaza Ho	no se rechaza Ho	no se rechaza Ho	se rechaza Ho
Justificación	p>0,05	p>0,05	p>0,05	p>0,05
Prueba de hipótesis	cpH - cpO	cpH - cpHayes	μH - μExperim	μH - μHayes
Probabilidad	0,159	0,48	0,5347	0,29
Consideración	no se rechaza Ho	no se rechaza Ho	no se rechaza Ho	no se rechaza Ho
Justificación	p>0,05	p>0,05	p>0,05	p>0,05
*Para valores de 5 a 20 ^oC

Leyenda:

ρH, cpH, kH y μH, propiedades termofísicas según ^{Hoffman (2006})

ρH, cpO, kO, propiedades termofísicas según ^{Orrego (2003})

μExperim, viscosidad determinada experimentalmente

ρHayes, cpHayes, kHayes y μHayes, propiedades termofísicas según Hayes

En todos los casos al comparar, se obtiene que no se rechaza la hipótesis nula, Ho, porque la probabilidad es mayor que 0,05.

Al analizar las medias de los valores obtenidos con los modelos reportados por ^{Bhuvaneswari y Anandharamakrishnan, (2014}), para la capacidad calorífica y la conductividad térmica de la cerveza se obtuvo que para ambas propiedades, el valor de P es menor que 0,05 por lo que la hipótesis nula, Ho, se rechaza al nivel de confianza del 95 %, los resultados obtenidos con el Statgraphics, se pueden observar en la Tabla 5.

Tabla 5 Resultados de las pruebas de hipótesis entre  

Modelos y/o valores analizados
Prueba de hipótesis	cpB- cpHayes	kB - kHayes
Probabilidad	0,00000390814	0,0234681
Consideración	Se rechaza Ho	Se rechaza Ho
Justificación	p<0,05	p<0,05

Leyenda:

cpB, kB, capacidad calorífica y conductividad térmica según ^{Bhuvaneswari y Anandharamakrishnan, (2014}).

Por todo lo analizado se considera que es adecuado el uso de los modelos reportados por ^{Hoffman (2006}) en la simulación, para utilizar el valor de las propiedades termofísicas, en el rango de temperaturas del proceso de pasteurización de cervezas.

CONCLUSIONES

El análisis de los modelos matemáticos para el agua, de datos de las propiedades termofísicas de alimentos en general y de los modelos para la cerveza, permitió validar a partir de los resultados de las pruebas de hipótesis, los modelos empleados por ^{Hoffman (2006}) correspondientes al agua, los que pueden ser utilizarlos para la estimación de las propiedades termofísicas de la cerveza, en el rango de trabajo del proceso de pasteurización, en estudios futuros de simulación.

REFERENCIAS

Abdulagatov, I.M., & Magomedov, U.B., Thermal conductivity of pure water and aqueous SrBr₂ solutions at high temperatures and high pressures. High temperatures -High-pressures, Vol. 35/36, No. 2. 2003, pp. 149-168.

Aparicio, C., Determinación de propiedades termodinámicas y acústicas a alta presión (desde 0,1 hasta 350 MPa) en líquidos. Aplicación a la industria alimentaria., Tesis presentada en opción al Grado Científico de Doctor en Ciencias Físicas, Facultad de Ciencias Físicas, Departamento de física de materiales, Universidad complutense de Madrid, España, 2009.

Augusto, P.E., Pinheiro, T., & Cristianini, M., Using Computational Fluid-Dynamics (CFD) for the evaluation of beer pasteurization: effect of orientation of cans., Ciência e Tecnologia de Alimentos, Vol. 30, No. 4, 2010, pp. 980-986.

Bird, R., Stewart, W., & Lightfoot, E., Fenómenos de transporte., Editorial Reverté, S.A., Barcelona, España, 1992, pp. 12.3-12.4

Bhuvaneswari, E., & Anandharamakrishnan, C., Heat transfer analysis of pasteurization of bottled beer in a tunnel pasteurizer using computational fluid dynamics., Innovative Food Science and Emerging Technologies, Vol. 23, June 2014, pp. 156-163.

Dilay, E., Vargas, J.V.C., Amico, S.C., & Ordonez, J.C., Modeling, Simulation and Optimization of a Beer Pasteurization Tunnel., Journal of Food Engineering, Vol. 77, No. 3, 2006, pp. 500-513.

Earle, R.L., Ingeniería de los alimentos., Editorial Acriba, S.A. Zaragoza, España, 1988, pp. 183-184.

Galán, C.E., Diseño de prototipo de viscosímetro y validación de uso en fluidos de alta, media y baja viscosidad., Tesis presentada en opción al título de Ingeniería Agroindustrial y de Alimentos, Facultad de Ingeniería y Ciencias Agropecuarias, Universidad de las Américas, Quito, Ecuador, 2018.

Girotti, D.H., Elaboracao de um modelo para o conttrole do proceso de pasteurizacao en cerveja envasada (in package)., Disertacao para ontencao do título de Mestre em engenharia, Universidade Federal do Río Grande do Sul, Porto Alegre, 2009.

Hayes, G., Manual de datos para Ingeniería de los alimentos., Editorial Acriba, S.A. , , Zaragoza, España, 1987, pp. 67-77.

Hernández, L.A., Diseño y puesta en marcha de un procedimiento para certificación de líquidos como patrones de densidad mediante el empleo del método de pesadas hidrostáticas, utilizando un sólido patrón de masa y volumen conocidos., Tesis presentada en opción al título de Licenciatura en Ingeniería Química, Universidad de Costa Rica, San José, Costa Rica, 2014.

Hoffman, K.L., Beer pasteurization models., Tesis presentada en opción al título de Máster en Informática y Modelación Matemática, Technical University of Denmark, Dinamarca, 2006.

Kern, D., Procesos de transferencia de calor., Editorial Continental, México, 1999, pp. 13-108.

Martínez, A., Análisis comparativo de compuestos bioactivos en cerveza artesanal y cerveza industrial., Trabajo final de grado presentado en opción del grado en nutrición humana y dietética, Universidad de Lleida, Lérida, España, 2015.

Martínez, Y., & Benítez, A., Métodos generalizados de estimación de propiedades de transporte: viscosidad., Monografía, Universidad de Matanzas “Camilo Cienfuegos”, Cuba, 2008.

Martínez, Y., & Benítez, A., Métodos generalizados de estimación de propiedades de transporte: Conductividad., Monografía, Universidad de Matanzas “Camilo Cienfuegos”, Cuba, 2009.

Montgomery, D.C., Desing and analysis of experiments., 9ª edición, Editorial John Wiley & Sons, Estados Unidos, 2017, pp. 33-38.

Nápoles, M.F., Pérez, M. y De la Cruz, M.L., Modelación matemática de la pasteurización de la cerveza utilizando dinámica de fluidos computacional., Centro Azúcar, Vol. 47, No. 1, 2020, pp. 67-76.

Orrego, C.E., Procesamiento de alimentos., Universidad Nacional de Colombia, 2003, pp. 75-76.

Patiño, L.A., Espinoza, H. y Velásquez, O., Estudio numérico de la transferencia de calor en la cerveza en el proceso de pasteurización., Revista Ciencia e Ingeniería, Vol. 22, No. 3, 2001, pp. 19-25.

Patiño, L.A., Espinosa, H., Collado, M. y Velásquez, O., Estudio del efecto de la presión dinámica de CO₂ sobre la distribución de velocidades y temperatura de la cerveza en el proceso de pasteurización., Saber, Universidad de Oriente, Vol. 17, No. 1, 2005, pp. 41-47.

Posada, G.J., Elementos básicos de estadística descriptiva para el análisis de datos., Editorial Luis Amigó, Medellín, Colombia, 2016, pp. 116-124.

Rosabal, J., & Garcell, L., Hidrodinámica y Separaciones mecánicas., Tomo 1, Editorial Félix Varela, La Habana, 2006, pp. 16-22.

Suárez, M., Cerveza: componentes y propiedades., Tesis presentada en opción al título de Máster Universitario en Biotecnología Alimentaria, Universidad de Oviedo, España, 2013.

Vargas, Z.P., Arteaga, S.R., Riera, G.G. & Cruz, V. L., Estimación de propiedades termofísicas de un producto cárnico., Tecnología Química, Vol. 40, No. 1, 2020, pp. 128-148.

Viera, R., López, S. & Levi, M., Modelación matemática para Ingenieros Químicos., Editorial Pueblo y educación, Ciudad de la Habana, 1988, pp. 35-36.

Walpole, R.E., Myers, R.H., y Myers, S.L., Probabilidad y estadística para ingenieros., Sexta edición, Editorial Pearson Educación, México, 1998, pp. 290-355.

Wong, G.E., ¿Después de un análisis de variancia…qué? Ejemplos en ciencias de alimentos., Agronomía mesoamericana, Vol. 21, No. 2, 2010, pp. 349-356.

Zegarra, Q., Propiedades térmicas de los alimentos- Balance de masa y otras variables en la industria frutícola - Factores que influyen en la evaluación sensorial de los alimentos., Tesis presentada en opción al título de Ingeniería en Industrias Alimentaras, Universidad Nacional de San Agustín de Arequipa, Perú, 2014.

Recibido: 21 de Julio de 2020; Revisado: 17 de Agosto de 2020; Aprobado: 31 de Agosto de 2020

^*Autor para la correspondencia: Misdelki Pérez, Email:[e-mail]

Los autores declaran que no existe conflicto de interés.

M.Sc. Misdelki Pérez Colas. Escribió y corrigió el artículo completo.

Dra.C. Martha Faustina Nápoles García. Participó en la escritura y corrección del artículo.

Dra.C. María de Lourdes de la Cruz Aragoneses. Colaboró en la escritura y corrección del artículo.