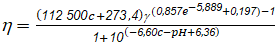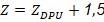INTRODUCCIÓN
La pandemia de Covid-19 ha puesto en evidencia la capacidad de respuesta, adaptación e investigación de la industria. En este sentido, General Motors, Ford, Ferrari y Tesla analizan cambiar su giro de negocio para fabricar respiradores artificiales para ayudar a los enfermos de coronavirus Zumba (2020). Las farmacéuticas han aumentado su capacidad modificando los procesos de producción para la fabricación a gran escala de la vacuna contra la Covid-19, Gail (2021).
Las recomendaciones sanitarias para eliminar los virus que pudieran estar en las manos incluye la higienización con gel hidroalcohólico (Martín-Vaquero y col., 2021). Debido al temor de contagio la demanda de desinfectantes de manos ha crecido en todo el mundo (BBC News Mundo, 2020). En el Ecuador ha proliferado la producción de gel antiséptico por microempresas improvisadas que no cumplen la normativa (ARCSA, 2020).
Conocer el producto que se demanda, su cantidad y sus criterios de calidad, así como las operaciones unitarias involucradas en su producción y la disponibilidad de materias primas es fundamental para el diseño y rediseño de plantas (Pérez y col., 2012).
El concepto de la Calidad desde la fase de Diseño (QbD) permite comprender el impacto de los parámetros del proceso en los atributos de calidad y la identificación y control de las fuentes de variabilidad (Rathore y Kapoor, 2016). En este sentido, los experimentos "in-silico" dentro del marco QbD contribuye significativamente al desarrollo eficiente de un proceso (Adam et al., 2011). Aunque la validez de los modelos empíricos está estrictamente limitada a la región de las condiciones probadas, estos podrían ser útiles en procesos de la industria farmacéutica (Fresno et al., 2001). Por otro lado, los indicadores dinámicos Valor Actual Neto (VAN) y Tasa Interna de retorno (TIR) mejoran cuando se optimiza la calidad, por lo que sugiere considerar la calidad desde la fase de diseño (Cerda y col., 2020).
Desde el inicio de la emergencia sanitaria en marzo del 2020 se registra el retiro de 8150 litros de alcohol artesanal, triplicando la cifra incautada en todo el 2019 (La Hora, 2020).
El objetivo de este artículo es diseñar un proceso que considere la calidad desde la fase de diseño para la producción de gel hidroalcohólico utilizando como materia prima principal el alcohol artesanal.
MATERIALES Y MÉTODOS
Para incrementar la aceptabilidad de los atributos de calidad y reducir la incertidumbre en los parámetros operacionales como parte del diseño del proceso se utilizó el procedimiento reportado por Cerda et al., (2021). En el mismo, los pasos a seguir son:
Análisis de datos experimentales y modelos matemáticos,
Simulación,
Determinación del número de productos defectuosos,
Determinación del nivel sigma de calidad del proceso,
Determinación de la incertidumbre (Metodología GUM).
El presente estudio se basó en la ecuación (1) de caracterización reológica del gel hidroalcohólico al 15 % publicada por Fresno et al., (2001).
Donde:
(: Viscosidad aparente (mPa s-1)
c: Concentración de polímero (en el intervalo 0,1 - 0,5 % w/w)
(: Velocidad de corte (en el intervalo 2 - 200 s-1)
pH: Potencial de hidrógeno (en el intervalo 4 - 7)
2.1 Datos experimentales y modelos matemáticos que correlacionan los parámetros operacionales y la calidad del producto final.
Los parámetros operacionales (pH, ( y c) fueron considerados como variables independientes y como variable dependiente el atributo de calidad ((). La variabilidad de la variable dependiente se determinó considerando los siguientes parámetros estadísticos: rango, desviación estándar y desviación media absoluta (Wolfram Research, 2010).
2.2 Simulación
Para la simulación se consideraron aleatoriamente 1 560 lotes por año en concordancia a la producción que se realiza en la Región Amazónica del Ecuador según lo reportado por Cerda et al., (2021).
La distribución de probabilidad de los datos experimentales se determinó considerando la mejor bondad de ajuste, mediante el software Wolfram Mathematica 12.2.
Se generan números aleatorios a partir de la distribución de probabilidad anterior utilizando Microsoft Excel. Los rangos utilizados en la primera iteración para este estudio de caso fueron tomados de Fresno et al., (2001). El número de muestras aleatorias generadas se estableció según la producción anual considerando el balance de masa.
Los modelos matemáticos y los números aleatorios obtenidos permitieron calcular los valores de la viscosidad en las correspondientes iteraciones.
2.3 Determinación del número de productos defectuosos.
A partir de los requerimientos de viscosidad como atributo de calidad del producto (variable dependiente) obtenidas de la simulación, se determinó los defectos por unidad (DPU) y el porcentaje de productos defectuosos. Para este caso de estudio, el valor objetivo fue de 1 500 (mPa s-1) ( 500 (mPa s-1) según Hands Clean, (2020).
2.4 Determinación del nivel sigma de calidad del proceso.
El nivel sigma de calidad de un proceso dado en la ecuación (2) se calculó para cada producción con base en su DPU según Abdelhamid (2003).
Donde Z es el nivel sigma de calidad y ZDPU es la distribución normal estándar correspondiente a la DPU.
También se determinan otras métricas de nivel sigma según lo propuesto por Keller (2011).
a) Defectos por millón de oportunidades (DPMO) ecuación (3):
Donde Oportunidades es el valor de las producciones.
b) Rendimiento (Yd) ecuación (4):
2.5 Análisis del nivel sigma de calidad del proceso
Se realizaron iteraciones hasta alcanzar al menos tres sigma en el proceso según lo recomendado por Alderete y col., (2003). Este valor equivale a una aceptación del 93,32 % del total de productos según Pulido y Salazar (2013).
2.6 Determinación de la incertidumbre por la metodología GUM
En cada iteración, se determinó la incertidumbre de los parámetros operacionales mediante la metodología GUM según Cerda et al., (2021) con el fin de reducir el rango de los parámetros operacionales hasta lograr una mayor aceptabilidad del atributo de calidad correspondientes a un nivel sigma mayor o igual a tres. Los pasos son:
Expresar matemáticamente la relación entre las magnitudes de entrada de medida (Y) (xi).
Determinar el valor estimado de las cantidades de entrada (xi) a partir del análisis estadístico de una serie de observaciones.
Evaluar la incertidumbre estándar de las magnitudes de entrada (u (xi)), donde la evaluación debe ser de tipo A o B.
Determinar la incertidumbre estándar combinada (uc (y)) para el mensurando, la incertidumbre para la cantidad de entrada y las covarianzas asociadas con las estimaciones de entrada.
Determinar el valor de la incertidumbre expandida (Up) para proporcionar un intervalo [y - Up; y + Up] donde Up = Uc(y) kp con kp = 1 (factor de cobertura).
2.7 Diseño del Proceso
Para estimar la disponibilidad de materia prima se consideró lo reportado por INEC- ESPAC, (2020), la superficie plantada de caña de azúcar para ser destinada a la producción de alcohol etílico, panela, melaza es de 17 870 hectáreas a nivel nacional. Según Figueroa (2008) si el etanol se extrae directamente del jugo de caña de azúcar el rendimiento se estima en 70 litros por tonelada de caña, mientras que la productividad de la caña de azúcar en Ecuador es de 78 toneladas por hectárea de caña. Del producto entre el rendimiento y productividad de la caña de azúcar se obtuvo un rendimiento de etanol de 5 460 litros por hectárea de caña. Para el balance de masa se utiliza SuperPro Designer versión 10 y se considera la formulación reportada por Fresno et al., (2001). La evaluación económica de la producción de gel hidroalcohólico se realiza según el método presentado por Peters et al., (2003), los precios de venta se utiliza los referenciales del mercado publicados en Ecuador INEC (2021).
RESULTADOS Y DISCUSIÓN
3.1 Análisis del modelo matemático que correlacionan los parámetros operacionales y la calidad del gel hidroalcohólico
El comportamiento estadístico de la viscosidad aparente como atributo de calidad del gel hidroalcohólico se muestra en la Tabla 1. El rango y la desviación estándar demuestran la gran variabilidad de este atributo, los valores mínimo y máximo están distantes. Esto concuerda con Cerda et al., (2021) ya que la incertidumbre de los parámetros operacionales c, (, y pH no ha sido optimizado.
Tabla 1 Comportamiento estadístico de la viscosidad (mPa s-1) del gel hidroalcohólico para una muestra de 1560 lotes
| 1199,42 | 1944,74 | 3782016,1 | 26567,52 | 5,14 | 26572,66 | 1296 | 1102,84 |
Los valores de c, (, y pH se generan con distribución de probabilidad uniforme continua, estos se corresponden con los valores reportados por Fresno et al., (2001), por tanto, esta distribución define mejor el recorrido de la variable, en divergencia con Cerda et al., (2021) pues la distribución beta que sugiere sería adecuada para variables aleatorias continuas que toman valores en el intervalo (0,1).
3.2 Análisis de la simulación
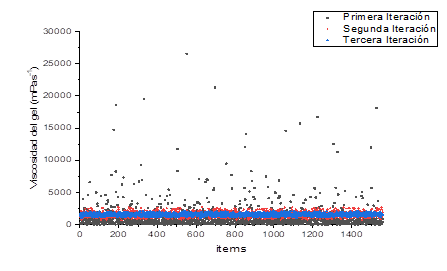
En la Figura 1 se observa a medida que se reduce la incertidumbre de los parámetros operacionales (c, ( y pH) en las sucesivas iteraciones, la viscosidad del gel se encuadra dentro del rango de especificación del producto, de tal manera que los productos defectuosos de la primera iteración son del 80,3 %, en la segunda iteración son del 18,9 % y en la tercera iteración se logró 0 % de defectos, es decir se alcanza el valor deseado de nivel sigma mayor a 3 en concordancia con lo reportado por Cerda et al., (2021).
3.3 Determinación y análisis del nivel sigma del proceso
El nivel sigma para una producción de 1 560 lotes en la primera iteración corresponde a 0,66 y la productividad 20,1 %, según Pulido y Salazar (2013) es necesario alcanzar al menos el 93,3 % de productividad para lograr un nivel sigma mayor a 3. Coincide con Alderete y col., (2003), quien manifiesta que el 93,32 % equivale a casi 6700 defectos por millón de oportunidades. Por consenso, las empresas han aceptado sigma 3 o sigma 4 como estándar (99,38 % es el estándar actual, equivalente a casi 6 250 defectos por millón de oportunidades).
En las iteraciones 2 y 3 se obtiene un nivel sigma de 2,31 y 3,50 y una productividad del 79 % y 97,7 % respectivamente.
3.4 Determinación de la incertidumbre por la metodología GUM
Se reduce el rango de cada parámetro operacional en cada una de las iteraciones. En la muestra estudiada es necesario 3 iteraciones para alcanzar un nivel sigma mayor a 3. Este nivel de calidad se alcanza para un rango de los parámetros operacionales de c (0,34 - 0,45 % w/w), ( (52,03 - 80,6 s-1) y pH (5,07 - 6,16), por tanto, para el diseño del proceso de gel hidroalcohólico se toman estos parámetros operacionales.
3.5 Diseño del proceso
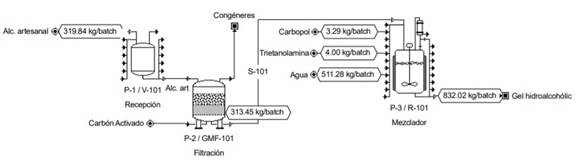
3.5.1 Balance de materiales
Para el presente estudio de caso se destina el 0,56 % de la superficie plantada en la provincia de Pastaza (INEC- ESPAC, 2020), lo que implica una disponibilidad de materia prima de 546 000 litros de etanol/1 560 lotes, es decir 350 litros de etanol/lote, con grado alcohólico promedio de 39 % V/V. En la Figura 2 se observa el esquema tecnológico basado en el procedimiento para la obtención de gel de Fresno et al., (2002), incluye la línea de alimentación al tanque de recepción donde es alimentado a un sistema de filtración con carbón activado para la eliminación de congéneres. El producto filtrado se deposita en un mezclador con agitación. Bajo estas condiciones la cantidad producida de gel hidroalcohólico es de 832,02 kg/lote. De acuerdo a la presentación del producto en el mercado se tendrían 832 envases de un kilogramo en cada lote a un precio de venta al público de 1 USD/unidad (INEC, 2021).
3.5.2 Dimensionamiento de equipos en las diferentes etapas del proceso
La variabilidad del producto resultante del proceso que satisface el intervalo del atributo de calidad provoca que exista una incertidumbre en el dimensionamiento del equipamiento, del balance de masa se obtienen las corrientes de entrada y salida en cada operación, con el SuperPro Designer v10.0 se obtiene el dimensionamiento dados los parámetros de diseño. En este caso se tienen tres tanques de recepción de 0,39 m3 de capacidad (altura 1,65 m; diámetro 0,55 m), un filtro de 0,18 m3 de capacidad (altura del lecho filtrante 0,23 m; diámetro del lecho filtrante 1 m) y un tanque de mezcla con agitador de 0,96 m3 de capacidad (altura 1,97 m; diámetro 0,79 m), la variable respuesta viscosidad aparente está influida por la concentración de polímero, velocidad de corte y potencial de hidrógeno. A partir de esta información se realizan los balances de materiales que proporcionan la capacidad de los equipos y se obtienen los parámetros de diseño.
3.6 Análisis y Factibilidad Económica
La producción de gel hidroalcohólico en tiempos de Covid-19, siempre que se garantice las especificaciones de calidad, constituye una oportunidad de inversión en razón que el capital total de inversión estimado es de 130 460 USD, desglosado en 110 880 USD de capital fijo de inversión (79 200 USD Costos directos y 31 680 USD de costos indirectos) y 19 580 USD de capital de trabajo, esto genera un retorno sobre la inversión de 295,5 %, periodo de recuperación al descontado de 0,3 años y un VAN de 1 842 551,68 USD.
Estos indicadores se logran siempre que no se tenga productos defectuosos, por lo tanto, los costos de no considerar la calidad desde la fase de diseño, serían de 1 042 229,76 USD/año si se considera los productos defectuosos de la primera iteración, y 245 306,88 USD/año en la segunda iteración. En la tercera iteración, no se tiene defectuosos. Por tanto, la selección del rango de parámetros operacionales influye en el cumplimiento de especificaciones de calidad y pérdidas económicas, ya que afecta los ingresos por la venta del producto.
CONCLUSIONES
El presente estudio de caso basado en los principios de la calidad desde el diseño infiere que en el proceso de producción de gel hidroalcohólico:
El porcentaje previsible de productos defectuosos disminuye a razón de la disminución de la incertidumbre de los parámetros operacionales llegando a cero % los productos defectuosos a medida que se alcanza el nivel sigma igual o mayor que tres y una productividad superior al 95% y los indicadores dinámicos como el retorno sobre la inversión de 295,5 %, el periodo de recuperación descontado de 0,3 años y el VAN de 1 842 551,68 USD son positivos.
Existe la necesidad de modelado y simulación de los atributos de calidad del producto para explicar el grado de dependencia con el dimensionamiento del equipamiento, sin embargo, con la viscosidad se obtiene una mejor comprensión de los parámetros operacionales del proceso que posteriormente serán controlados en la fase de operación.