ARTÍCULO ORIGINAL

 

Optimización del proceso de enriquecimiento proteico del bagazo de caña de azúcar

 

Process optimization of protein enrichment of sugar cane bagasse

 

 

Dra. C. María Caridad Julián-Ricardo, Dr. C. Luís Beltrán Ramos-Sánchez

Departamento de Ingeniería Química, Universidad de Camagüey "Ignacio Agramonte Loynaz". Camagüey. Cuba. [e-mail]

 

 

---

RESUMEN

La importancia de los procesos de fermentación en estado sólido que se desarrollan en el presente hace indispensable la aplicación de la optimización en el diseño de sistemas nuevos y para la toma de decisiones en los ya existentes. El proceso tecnológico para una capacidad productiva de 100 t/d de producto seco, incluye la preparación del medio de cultivo, el enriquecimiento proteico en biorreactores de lecho fijo y el acondicionamiento y terminación del producto. El objetivo de este trabajo es optimizar el proceso de enriquecimiento proteico del bagazo de caña de azúcar a partir de la determinación de los valores de las variables de operación en el biorreactor: tiempo de residencia y flujo específico de aire que minimizan el costo de producción unitario. La optimización del proceso se programó de forma modular sobre MATLAB 7.8 (2009). La solución óptima dio un tiempo de residencia en el biorreactor de 11,8 horas y un flujo específico de aire de 1,3 L kg^-1 min^-1. El costo de producción unitario mínimo en estas condiciones fue de 746,73 $/t PV. El análisis de sensibilidad permitió determinar que el proceso es estable alrededor del óptimo.

Palabras claves: optimización, enriquecimiento proteico, fermentación en estado sólido, biorreactores.

---

ABSTRACT

The importance of the processes of solid state fermentation taking place in this indispensable application of optimization in the design of new systems and for decision-making in the existing ones. The technological process have a production capacity of 100 t/d of dry product, including the preparation of the culture medium, the protein enrichment in fixed bed bioreactors, packaging and product completion. The main goal of this work is to optimize the process of protein enrichment of sugar cane bagasse from the determination of the values of the variables in the bioreactor operation: residence time and specific air flow, minimizing the cost of production unit. The process optimization was programmed modular lyon MATLAB 7.8 (2009). The optimal solution gave a residence time in the bioreactor of 11,8 hours and a specific air flow of 1,3 L kg^-1 min^-1. The minimum unit cost of production in these conditions was 74673 $/t PV. Sensitivity analysis allowed us to determine that the process is stable around the optimal.

Keywords: optimization, protein enrichment, solid state fermentation, bioreactors.

---

 

 

INTRODUCCIÓN

La optimización en la solución de un problema surge por la necesidad de minimizar recursos y esfuerzos. La necesidad y sobre todo la posibilidad de optimizar se hace patente cuando se procede a diseñar tecnológicamente un proceso. El objetivo de la optimización en el diseño de una instalación de procesos de la industria química es encontrar la mejor solución basada en algún criterio de efectividad o comportamiento [1]. Se puede definir como optimización al proceso de seleccionar, a partir de un conjunto de alternativas posibles, aquella que satisfaga el o los objetivos propuestos. Para resolver un problema de optimización se requieren dos etapas principales: la formulación del modelo y la resolución y validación [2].

Los objetivos típicos para diseño de procesos incluyen el costo de inversión, el costo de operación, el rendimiento de los productos y la ganancia total. Los problemas de optimización que tienen objetivos y/o restricciones no lineales de las variables se denominan problemas de programación no lineal [3].Un diseño óptimo se basa en las mejores o más favorables condiciones del proceso. Generalmente las condiciones óptimas se reducen a consideraciones de costo-beneficio. De esta manera, un diseño económico óptimo puede estar basado en las condiciones para obtener un mínimo costo por unidad de tiempo o un máximo beneficio por unidad de producción [4].Pero pueden darse diferentes situaciones, por ejemplo, puede encontrarse un menor costo inicial y mayores costos de operación o un costo inicial más alto y en luego menores costos de operación. Por lo que resulta indispensable efectuar la evaluación económica. Muchos estudios indican que los modelos básicos de ingeniería económica del Flujo de Caja, Valor Actual Neto y Tasa Interna de Retorno son los más utilizados [5].

El biorreactor es el centro de los procesos fermentativos. La maximización de la velocidad de formación y el rendimiento de productos dentro del biorreactor es una parte importante en la optimización de los procesos productivos. En contraste con la fermentación sumergida, la fermentación en estado sólido (FES) está aún en la búsqueda de un alto grado de desarrollo, principalmente por los problemas que se presentan en las camas de sólidos, dados fundamentalmente, por el pobre mezclado, las características de la transferencia de calor y el manejo del material [6].

Los procesos de FES durante años han sido poco estudiados. Los avances más notables en relación con la optimización de procesos son recientes y han llegado hasta la modelación matemática, que como se ha reiterado en las últimas publicaciones "Los modelos matemáticos son una importante herramienta en la optimización del diseño y operación de los biorreactores para fermentación en estado sólido" [7].Se dan pasos en la aplicación de la modelación para la simulación de los procesos de FES y establecer estrategias de mejoras que se han validado sólo a pequeña escala, que aparecen recogidas en las referencias mencionadas, pero aún no se ha trabajado en la optimización de procesos de FES. La importancia de los procesos de FES que se desarrollan en el presente hace indispensable la aplicación de la optimización en el diseño de sistemas nuevos y para la toma de decisiones en los ya existentes.

El modelo técnico-económico desarrollado en este trabajo permitió optimizar el proceso de enriquecimiento proteico del bagazo de caña de azúcar a partir de la determinación de los valores de las variables de operación: tiempo de residencia y flujo específico de aire, que minimizan el costo de producción unitario.

 

MATERIALES Y MÉTODOS

El flujo tecnológico se planteó teniendo en cuenta los resultados del trabajo experimental y de simulación [8] y los pasos propuestos para el diseño de productos químicos y de procesos [9].

Descripción del Flujo Tecnológico

En la figura 1 aparece un diagrama de bloques que representa las principales etapas del proceso. En la primera etapa se mezclan las materias primas y se inoculan con levadura fresca, producida in situ mediante fermentación sumergida. La mezcla se alimenta a los biorreactores de lecho fijo, donde el medio de cultivo permanece dentro del equipo durante todo el tiempo de residencia y se le suministra un flujo de aire continuo que entra por el fondo y sale por el tope, proveniente de la torre de humidificación, que le garantiza la humedad requerida por el proceso. A continuación, el producto húmedo pasa al secador, que emplea aire caliente para la obtención del producto seco, que se muele, se prensa y se envasa.

Diseño óptimo del proceso

El trabajo de desarrollo tecnológico realizado hasta el momento, centra su atención en el área de enriquecimiento proteico, buscando un modelo que sea suficientemente robusto para simular su comportamiento y establecer las condiciones en las que se alcanza el máximo de eficiencia técnico-económica de la instalación, por la intensificación del proceso. De esta manera, la tarea de optimización definida en este trabajo tiene como objetivo determinar los valores de las variables de operación en estudio, que minimicen los costos de producción.

Función Objetivo, variables a optimizar y restricciones

En la optimización se plantea como función objetivo el costo de producción unitario, por tonelada de proteína verdadera (PV) obtenida en el proceso de FES. Este criterio está en relación directa con la eficiencia técnico-económica del proceso y revela los aspectos contradictorios de las variables a optimizar que dan lugar a la existencia de una solución de compromiso. La ecuación que define a este costo es:

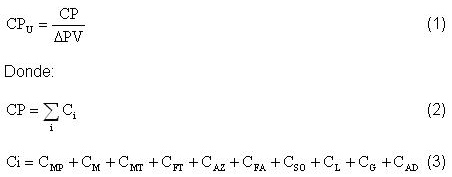
El incremento de proteína verdadera en el producto final se determinó por simulación del proceso de FES 8 a partir de un modelo matemático validado en un biorreactor de lecho fijo de 100 L, incluye el balance de masa para el crecimiento de la biomasa y para el consumo de sustrato y el balance de energía con un modelo pseudo homogéneo.

Las variables de mayor interés en la operación del biorreactor son: el tiempo de contacto y el flujo específico de aire. Tiempos de residencia pequeños dan lugar a una planta más productiva por lo que la inversión es pequeña y el costo anual menor pero, en esas condiciones se produce poca proteína pudiendo dar lugar a costos unitarios elevados. Por otro lado, tiempos de residencia grandes permiten un máximo crecimiento de la proteína pero decae la productividad, crece la inversión y también el costo de producción anual. Es decir habrá un cierto valor intermedio de esta variable que minimice el costo unitario.

En el caso del flujo específico de aire, cuando es elevado, los perfiles de temperatura tienden a ser más homogéneos y la operación a ser isotérmica, a la temperatura óptima. De esta manera se maximiza la producción de proteína. Este escenario produce, en cambio, la necesidad de un soplador y de una torre de humidificación grandes, pudiendo producir una elevación del costo anual, asociada al mayor consumo de electricidad y mayores niveles de amortización. Niveles en el otro extremo producen el mismo efecto pero por otras causas, lo que demuestra la existencia de niveles de compromiso entre esos extremos.

Las restricciones que se identifican en estas variables son de orden físico pues ambas deben ser siempre positivas. Otra restricción del sistema está asociada a las dimensiones de los equipos que componen la planta pues las ecuaciones empíricas desarrolladas para estimar su costo de adquisición tienen ciertos límites en dependencia de la fuente empleada.

Estimación del costo de producción

Los componentes Ci del costo de producción se estiman por la metodología desarrollada por Peters y Timmerhaus 4 y se detallan a continuación:

Costo de las materias primas: El costo de las materias primas empleadas para la producción se determinó como lo hizo Ramos 10 , resultó ser 50,30 $/t de producto seco.

Costo de los materiales de producción: Este componente tiene en cuenta el consumo de catalizadores, solventes y otros materiales que no se emplean en este proceso.

Costo de mantenimiento o reparación: Se estima considerando que se trata de una planta con nivel de severidad promedio, en un 5 % del valor económico total de la instalación.

Costo de la fuerza de trabajo utilizada en el proceso productivo: Se consideró que la planta requiere tres unidades tecnológicas.

El costo se estimó como el producto del índice salarial promedio (ISP) de los trabajadores del MINAZ por el total de trabajadores-horas/año (RT), por las 3 unidades que componen la planta y por el tiempo laboral anual (tL), que son 334 d/año (ecuación 5). El índice salarial promedio se calculó para un salario de 400 pesos mensuales (Reportado por la Delegación del MINAZ en Camagüey), obteniéndose 2,0833 pesos/(t h). El número de trabajadores-horas/año necesarios para operar la totalidad de los equipos se determinó en función de la capacidad de diseño de la planta 4 . Se utilizó el criterio de plantas químicas con condiciones promedios, se seleccionó la curva B de la figura 6-8, p. 198 y se obtuvo, para la capacidad de 100 t/d, que se requieren 46 (trabajadores h)/(d unidad tecnológica).

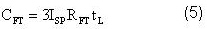
Amortización: Estimada a partir del valor económico inicial de la planta, ecuación (6) y del tiempo de vida útil, ecuación (7).

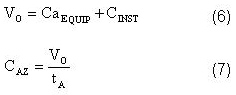
Las ecuaciones del costo de adquisición de los equipos principales se determinaron en función de las dimensiones fundamentales de cada equipo, mediante un análisis de regresión en los nomogramas correspondientes presentados por Peters y Timmerhaus 4 , empleando los Indicadores Económicos actuales. Para la estimación del costo de instalación se aplicó el Método C "Porcentaje del costo del equipamiento requerido" 4.

Costo de facilidades auxiliares: Se incluye el consumo de agua, de bagazo como combustible y de energía eléctrica, que se adquieren de la propia industria azucarera donde se ubica la planta. Para el cálculo de estos consumos se hizo necesario pasar a la etapa de ingeniería de detalle, aplicando el método A, de Peters y Timmerhaus 4 . El trabajo se realizó por etapas, según el servicio requerido por los equipos en operación, en todos los casos se tuvo en cuenta que la planta trabaja de forma continua, 334 días al año, determinándose el índice de consumo de agua (IC_W), el índice de consumo de electricidad (IC_ELECT) y el de combustible (IC_COM). Se paga 0,09 $/kW h, por el consumo de agua para proceso 0,05 $/m³ y el costo del combustible (bagazo) 8,05 $/t.

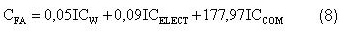
Costo de suministros de operación: Se incluyen los lubricantes y grasas empleados en los equipos, así como otros suministros que se necesitan durante la operación de la planta. Se calculó como el 15 % del costo total de mantenimiento o reparación.

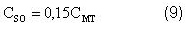
Costo de laboratorios: Contienen los gastos económicos para pagar los salarios del personal que asegura la realización de los análisis de laboratorio requeridos para el control de la calidad de la producción y en general para el control del proceso. Se determinó como el 10 % del costo de la fuerza de trabajo directa de la planta.

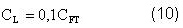
Costos generales: Están constituidos por el salario del personal técnico que no trabaja directamente en la producción, el costo de servicios médicos, costo de comedores y facilidades recreativas, costo de los servicios de protección, costo de almacenes, mantenimiento de edificios, costo de electricidad en edificios y otros gastos. Se calcularon como el 50 % de la suma de los gastos en la fuerza de trabajo directa y en mantenimiento.

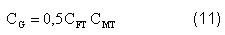
Costos de administración o dirección: Se incluye el salario del personal administrativo, costo de materiales de oficina y costo de comunicaciones externas. Se calculó como un 40 % del costo de la fuerza de trabajo directa.

Implementación de la optimización en MATLAB

Se confeccionaron siete módulos en MATLAB 7.8 (2009) para la optimización del proceso, a continuación se presenta la descripción de cada uno de ellos:

1. Se plantearon las ecuaciones que permiten calcular el costo de cada equipo, mediante su suma se calcula el costo del equipamiento y se introducen los índices de costo, que permiten calcular el costo actualizado del equipamiento.
2. Se incluyen los por cientos asumidos para cada componente del costo de inversión, las expresiones para el cálculo del costo de cada uno de sus componente y la expresión para el obtener la inversión total.
3. Se plantearon las expresiones para el cálculo de los componentes del costo de producción y su sumatoria para obtener el costo de producción anual.
4. Se incluyeron las ecuaciones auxiliares, dentro de las que se encuentran las utilizadas para el cálculo del volumen y el número de los biorreactores.
5. Se programó la función objetivo.
6. Se programó la simulación gráfica de la función objetivo, del crecimiento de la proteína, del consumo de azúcares reductores y del número de biorreactores, para mediante una exploración ubicar la región del óptimo.
7. Se planteó la expresión para la optimización de la planta, que utiliza la función LSQNONLIN que se caracteriza porque puede dar soluciones locales de la función objetivo, empleando primero el método interior reflexivo de Newton o pueden emplearse opciones con la función OPTIMSET y aplicar el método de Levenberg-Marquart o el de Gauss-Newton; con esta función pueden modificarse además el número de iteraciones, el número máximo de evaluaciones y la tolerancia relativa de la solución. Se introduce una solución inicial y los límites inferior y superior, que se requieren para comenzar la búsqueda.

 

RESULTADOS Y DISCUSIÓN

Elección de la capacidad productiva

La demanda existente de este producto en la provincia supera varias veces la capacidad que se podría instalar en un ingenio azucarero de esta región, de acuerdo a la disponibilidad de materias primas. En estas condiciones, la capacidad a diseñar tendrá que hacerse en función de estas limitaciones en el lugar donde se decida montar.

Para estimar el impacto de esta tecnología se decidió escoger una capacidad productiva de 100 t/d de producto seco, que se encuentra en un orden de magnitud cercano al de la planta de Saccharina que se construyó a finales de los años 80 en la Empresa Azucarera Siboney.

Exploración del espacio de las variables

Se efectuó una exploración gráfica para ubicar la región del óptimo y hacer la selección de los valores iniciales para la optimización.
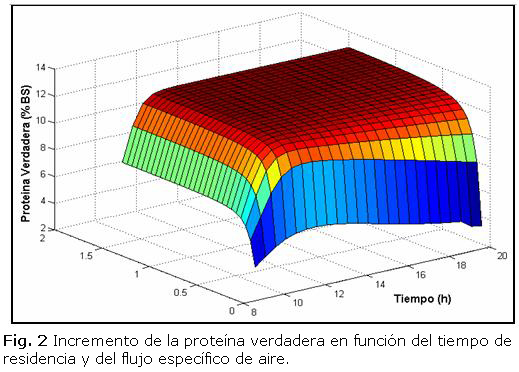
El crecimiento de la proteína verdadera se examinó para las variables tiempo de residencia en el rango de (8-20) h y flujo específico de aire entre (0,1-1,5) L/(kg min). Los resultados obtenidos se muestran en la figura 2. La proteína tuvo un crecimiento acorde a lo esperado, alcanzó su valor máximo alrededor de las 11 horas.

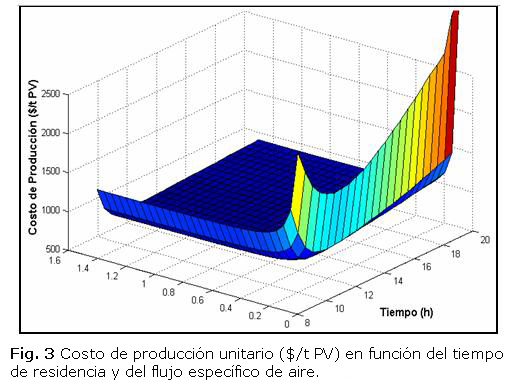
En la figura 3 se puede observar que el costo unitario mínimo se ubica en la zona que corresponde al tiempo entre (11-12) h y el flujo específico de aire es favorable a partir de 0,4 L/(kg min).

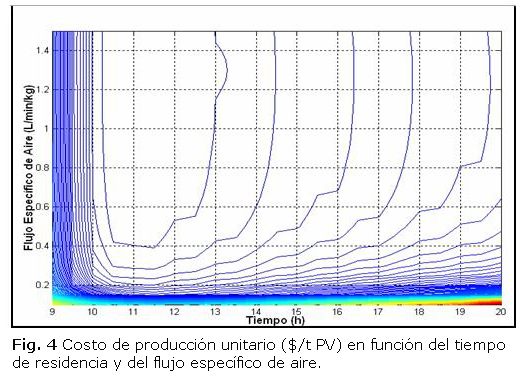
En la figura 4 se muestra una representación del contorno de la función objetivo para ambas variables. Es visible que el tiempo de residencia tiene la región óptima en el rango de 10 a 13 horas de fermentación. En el caso del flujo específico de aire, al existir poca sensibilidad del costo unitario a partir de 0,4 L min^-1 kg^-1, el contorno no llega a cerrar, pero con este resultado de la simulación se pudo ubicar, al menos el nivel inferior de éste.

Solución óptima del proceso

Se ejecutó la optimización, que terminó satisfactoriamente y dio como solución óptima un tiempo de residencia de 11,8 horas y un flujo específico de aire de 1,3 L kg^-1 min^-1. El costo de producción unitario mínimo en estas condiciones fue de 746,73 $/t PV.

Análisis de sensibilidad del punto óptimo

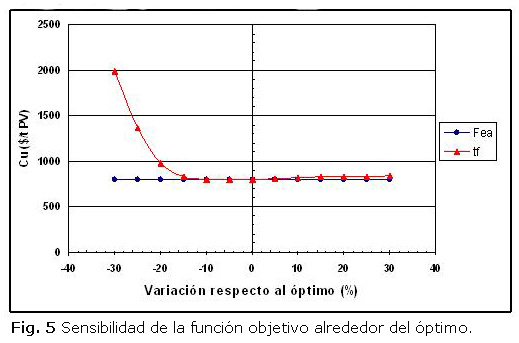
El análisis de sensibilidad se hizo con la evaluación de la función objetivo modificando una variable en el rango de -30 % y +30 % y manteniendo la otra fija en su nivel óptimo, tanto para el tiempo de residencia como para el flujo específico de aire. Al valor correspondiente al óptimo se le asignó una desviación de cero por ciento.

Se observa en la figura 5 que el tiempo de residencia es muy poco sensible a diferencias por encima del valor óptimo, y también a variaciones hasta un 10 % por debajo del valor óptimo, para variaciones mayores si se hace muy sensible. En cuanto al flujo específico de aire, el punto óptimo prácticamente no es sensible, en el rango donde se efectuaron las desviaciones. Lo que permite un proceso estable alrededor del óptimo.

 

CONCLUSIONES

El modelo técnico-económico desarrollado en este trabajo permitió optimizar el proceso de enriquecimiento proteico del bagazo de caña de azúcar. La solución óptima dio un tiempo de residencia en el biorreactor de 11,8 horas y un flujo específico de aire de 1,3 L kg^-1 min^-1. El costo de producción unitario mínimo en estas condiciones fue de 746,73 $/t PV. El análisis de sensibilidad permitió determinar que el proceso es estable alrededor del óptimo.

 

NOMENCLATURA

Ca- Costo de adquisición; $
C_AD - Costos de administración; $
C_AZ - Amortización; $
C_COM - Costo de combustible; $
C_ELECT - Costo anual de energía eléctrica para la planta; $
C_FA - Costo de facilidades auxiliares; $
C_FT - Costo de fuerza de trabajo; $
C_G - Costos generales; $
C_i - Componentes del costo de producción; $
C_INST - Costo de instalación; $
C_L - Costo de laboratorios; $
C_M- Costo de materiales para la producción; $
C_MP - Costo de las materias primas; $
C_MT - Costo de mantenimiento; $
CP- Costo de producción; $ a^-1
CP_U - Costo de producción unitario; $ kg ^-1 PV
C_SO - Costo de suministros de operación; $
C_W - Costo del agua; $
I_SP - Índice salarial promedio; $/(t h)
PV- Concentración de proteína verdadera; % BS
R_FT - Requerimiento de fuerza de trabajo; trabajadores -h/d
t_A- Tiempo de vida útil de la planta; años
t_L- Tiempo laborable anual; d/año
V_ET -Valor económico total de la instalación; $
V_O - Valor económico inicial de la planta; $

 

BIBLIOGRAFÍA

1. MONTAGNA, Jorge Marcelo. "Optimización de procesos por computadora". Edición N. J. Scenna. Buenos Aires, 2001. p. 497-534.

2. FERRERO, Marta B. y CHIOTTI, Omar. "Optimización". Edición N. J. Scenna. Buenos Aires, 2001. p. 435-496.

3. BOIZÁN, Meinardo. Optimización. Editorial Pueblo y Educación. Ciudad de La Habana, Cuba, 1988. 294 p.

4. PETERS, Max. and Timmerhaus, Klaus. Plantdesign and economics for chemical lengineers. Fourth Edition. Singapur: McGraw-Hill International Editions, 1991. 910 p. ISBN: 0-07-100871-3

5. OQUENDO, Hilda. "Alternativas del desarrollo prospectivo de los derivados de la caña de azúcar". Universidad de Camagüey, Camagüey, 2002.

6. MITCHELL, D. A., et al."A model-based investigation of the potential advantages of multi-layer packed beds in solid-state fermentation".Biochemical Engineering Journal, 2010, vol. 48 p. 195-203.

7. MITCHELL, D. A., et al., "Future Prospects for SSF Bioreactors". (Eds.). Berlin: Springer, 2006. p. 413-416.

8. JULIÁN, M. C., RAMOS, L. B., GÓMEZ, A. O. "Simulación de un biorreactor de lecho fijo a escala industrial". Tecnología Química, 2012, vol. XXXII, núm. 1, p. 12-18.

9. Seider, W. et al. Product and process design principles. Second edition. John Wiley and Sons, 2003.

10. RAMOS, L. B. "Aplicación de la Modelación Matemática para el Desarrollo de la Tecnología de Fermentación del BAGARIP". Camagüey, 2000.

 

 

Recibido: Diciembre 2013
Aprobado: Mayo 2014

 

 

Dra. C. María Caridad Julián-Ricardo.Departamento de Ingeniería Química, Universidad de Camagüey "Ignacio Agramonte Loynaz". Camagüey. Cuba. [e-mail]