ARTICULO ORIGINAL

 

Análisis in silico de un cultivo de células de mamíferos en biorreactores semicontinuos de dos etapas

 

In silico analysis of a mammalian cell culture in two stage fed-batch bioreactors

 

 

Dr.C. Luis B. Ramos-Sánchez, MSc. Diana D. Alcalá Galiano-Morell, MSc. Héctor E. Sánchez-Vargas, Dra.C. Mariela Rizo-Porro

Departamento de Ingeniería Química. Universidad de Camagüey "Ignacio Agramonte Loynaz". Camagüey. Cuba. [e-mail]

 

 

---

RESUMEN

El objetivo de este trabajo es comparar un sistema de cultivo de células de mamíferos semicontinuo en dos etapas con uno de simple etapa. Se utilizaron las técnicas de diseño in silico para intensificar la producción de anticuerpos monoclonales (AcM) en ambas variantes antes de compararlas. Se utilizó como caso de estudio un modelo cinético mixto de células de hibridoma reportado en la literatura. La simulación computacional se realizó utilizando la plataforma computacional MATLAB . Los resultados demostraron que en un sistema semicontinuo de doble etapa, pudiera lograse una productividad significativamente mayor de AcM que en uno de simple etapa. En el caso estudiado, en doble etapa, con una fracción de volumen de la primera etapa del 80 %, se alcanzan incrementos de las concentraciones del AcM del 58 % respecto a la variante de simple etapa; lo que representa un incremento de productividad del AcM de un 30 %.

Palabras claves: cultivo de células, anticuerpos monoclonales, optimización, biorreactor semicontínuo de dos etapas.

---

ABSTRACT

The objective of this work is to compare a two-stage fed-batch culture system of mammalian cells with a single culture system. In silico process-design techniques were used in order to intensify the production of monoclonal antibodies in both cases before comparing them. As case study a structured kinetic model reported in literature for an industrial process of monoclonal antibodies (MAb) harvested from cultures of hybridoma cells was selected. Computational simulation was carried-out using MATLAB software as computing platform. Results demonstrated that in this particular case a two-stage fed-batch culture system produces higher productivities in MAb production compared to simple stage systems. In double stage systems, having a fraction of volume of the first stage of 80 %, an increment of 58 % in MAb concentrations and 30 % in productivity were obtained when compared to a single stage system.

Keywords: Cell culture, monoclonal antibodies, optimization, two-stage semi-continuous bioreactor.

---

 

 

INTRODUCCION

La producción de proteínas con fines terapéuticos en células de mamíferos es actualmente una rama productiva de atractivos económicos, tanto por los volúmenes actuales de ventas como por el ritmo de crecimiento observado en años recientes [7]. Hay cifras muy alentadoras. Por ejemplo, en el año 2004, el mercado global de proteínas terapéuticas fue de 44 billones de USD y para el 2010 se estimó en 70 billones de USD [17]. De todo este mercado, sólo las ventas de anticuerpos monoclonales se estimaron en 35 billones de USD en el año 2009 [13]. Así mismo, según citan [ 9 ] en un reporte del 2007 se estimaba que el mercado biotecnológico en general se duplicará hacia el 2020.

Las células de mamíferos constituyen actualmente el sistema de expresión preferido para la obtención de proteínas con aplicaciones médicas. Esto se debe a su capacidad de sintetizar proteínas muy complejas que requieren grandes modificaciones post-traslacionales [3]. Sin embargo, los altos niveles de inversión y los elevados costos de investigación en los que se incurre, así como los notables tiempos de cultivo necesarios en este tipo de sistema, demandan de una reducción de costos y del tiempo necesario para colocar los productos en el mercado [16]. En esencia, se necesita identificar las condiciones óptimas para que estas células expresen la mayor cantidad de proteína con el menor gasto.

En la solución de este tipo de problemas existe un creciente uso de estrategias de investigación basadas en el diseño in silico de procesos, es decir, usando la modelación matemática y la simulación de procesos [19]. Esta estrategia ofrece importantes ventajas respecto a las empíricas que aún se utilizan [10], brinda la posibilidad de comprensión cabal del proceso, complementa el conocimiento ya disponible con nuevos datos y reduce el tiempo y el costo de desarrollo del producto. El diseño de procesos se resuelve entonces acudiendo a los métodos de optimización [20], con auxilio de la simulación computacional.

Hasta la fecha se han utilizado diferentes sistemas de cultivo, pero los más frecuentes son los biorreactores de tanque agitado en operación semicontinua (BSCTA) y los biorreactores continuos con perfusión (BCTAP), ambos en simple etapa [8]. El BSCTA (fed-batch) es muy empleado mundialmente en la actualidad por su simplicidad y buenos resultados [5; 6]. En la práctica se emplean perfiles de alimentación variables con vistas a conseguir el mejor desempeño del proceso [2; 14]. A partir del trabajo de [1], se ha estimado un valor de productividad de anticuerpo en un BSCTA de 5 g año ^-1 L ^-1. Este valor es bajo comparado con los resultados de [11], de los que se estimó una productividad de 55,24 g año ^-1 L ^-1 , luego de realizar cambios en la operación del biorreactor en un sistema continuo con perfusión. Estos niveles de productividad estimados de la literatura muestran el potencial diferente de estas dos operaciones, sin embargo, se puede afirmar que aún son bajos y no lograrán suplir la creciente demanda de productos basados en AcM [4].

Las estrategias de cultivo relacionadas con cambios en la estructura del sistema de contacto ha sido poco tratada. Recientemente se demostró teóricamente que con un sistema de dos etapas se puede incrementar la productividad del proceso [18]. En el reporte realizado no se estimó en qué medida podrían lograrse las mejoras. Resulta interesante que no se han encontrado reportes previos de diseños de BSCTA operando con flujos constantes pero diferentes en dos etapas. Este proceso es práctico para su inserción en la práctica industrial y no necesitaría cambios en las instalaciones existentes, solo en las variables operativas.

El presente trabajo tiene como objetivo diseñar por técnicas de diseño in silico la operación de un BSCTA en dos etapas para el cultivo de células de mamíferos, tomando un caso de estudio previamente reportado [13; 14].

 

MATERIALES Y METODOS

Sistemas de cultivo de células

Se trabaja con un BSCTA con perfil de flujo constante en dos variantes. La variante I es de una sola etapa y es bien conocida. Al tanque se alimenta un flujo constante durante todo el proceso hasta que se llena el volumen efectivo, luego de lo cual se realiza la cosecha del producto. En la variante II el volumen efectivo del biorreactor se divide en dos partes y se aplica una política de alimentación para la primera parte con el fin de maximizar la producción de biomasa, tal como se desprende de [18]. Para la otra, cambia la política de alimentación y se persigue maximizar la producción de la proteína. El diseño persigue como objetivo establecer los flujos óptimos para alcanzar la meta de cada etapa.

Caso de estudio utilizado

Se trata del reportado por [14], relacionado con una célula de hibridoma productora de un anticuerpo en producción a escala industrial. Es el mismo proceso analizado en [18].

Modelos matemáticos del sistema de cultivo celular en estudio

Un balance de masa macroscópico fue realizado para representar las diferentes fases de los sistemas de cultivo. El proceso se consideró isotérmico y se asumió mezcla perfecta en el interior del recipiente. No se consideró la ocurrencia de limitación del crecimiento celular por falta de oxígeno. La concentración de algunas especies químicas tales como la glucosa (GLC), la glutamina (GLN), el lactato (LAC) y el amoniaco (AMN) se incluyeron en los balances de masas. Además, también se tuvieron en cuenta las concentraciones de células viables y muertas, así como la concentración del AcM.

El modelo matemático que representa las ecuaciones de la (1) a la (7) son válidas para ambas variantes.

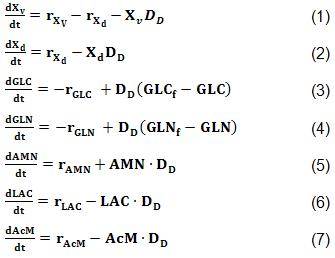
El modelo cinético y sus parámetros fueron tomados del caso en estudio antes definido, pero sus ecuaciones de velocidad fueron tomadas en la forma que se reportó por [18].

Definición del modelo de optimización

Se realizó una optimización de ambas variantes, simple etapa y doble etapa, antes de comparar los sistemas de cultivo celular (SCC) estudiados.

Función objetivo

Para el sistema de simple etapa se tomó la productividad anual de AcM (ecuación 9) como criterio de efectividad. La optimización de la segunda variante se realizó de acuerdo con la tesis planteada en el trabajo precedente [18], según la cual, primero debe hacerse crecer la biomasa y luego hacer que ésta produzca el AcM. Así pues, en la primera etapa se optimizó en función de maximizar la productividad en biomasa (ecuación 8), mientras que en la segunda se hizo en función de maximizar la productividad del AcM (ecuación 9).

La expresión para el cálculo de la productividad para estos SCC se definió como:

La masa de AcM producida por año de trabajo fue calculada como:

El término n_gf incluye la eficiencia global de fermentación y los pasos de recobrado empleados en la producción del AcM. Este parámetro fue estimado en 0,85 considerando la producción promedio de una proteína de una planta industrial de referencia [12].

El número ciclos productivos anuales fue calculado como:

El fondo de tiempo anual disponible t_a fue fijado en 7 920 horas, mientras que el tiempo de fermentación de un ciclo fue calculado como la suma del tiempo de preparación y el de fermentación:

Selección de las variables de diseño

Para la variante I se seleccionaron como variables de diseño la velocidad de dilución estática (D_E) y la concentración de glucosa en el alimentado (C_GA). La D_E, para el perfil de flujo constante se calculó con el volumen total efectivo a llenar (V_T), según la ec. (13):

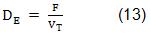
La D_E es constante, lo cual permite calcular el flujo volumétrico de alimentación (F) para un valor fijo del volumen. La velocidad de dilución dinámica (D_D), sin embargo, es utilizada en el modelo matemático de este sistema y varía en la medida en que se va llenando el biorreactor.

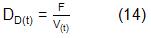
La concentración de glucosa en el alimentado se varió según el rango utilizado por Kiparissides, entre 10 y 500 mM [14]. Esta variable tiene gran influencia en los perfiles de concentración que se imponen en el sistema, al igual que la velocidad de dilución estática.

Para la variante II se estudió el efecto de la D_E para cada etapa (ec. 13), de la fracción de volumen de la primera etapa (f_V) y de la concentración de glucosa en la alimentación. El rango para el estudio de la glucosa fue el mismo que en la variante anterior. El factor f_V representa la parte del volumen total efectivo que es dedicado a la primera etapa, ec.(15):

El término f_V representa una variable nueva en el diseño de estos sistemas. No hay referencias de cuál debe ser su valor, pero como la fracción está entre cero y uno, se estudió en ese intervalo. Mientras mayor sea f_V, mayor será la cantidad de biomasa que almacene la primera etapa y la síntesis de AcM en la segunda [18].

No se consideran otras variables de diseño como la velocidad de agitación, la concentración de sustratos o la temperatura, porque este es un modelo simplificado en el que no se consideran los efectos no isotérmicos, la transferencia y consumo de oxígeno, ni las cuestiones relacionadas con el costo de producción. El trabajo se enfoca más en las variables principales del sistema relacionadas con la productividad y su único objetivo es demostrar la tesis antes planteada [18].

Parámetros invariables del sistema

Los parámetros del sistema fueron fijados en el mismo nivel para ambas variantes. El volumen total del fermentador es de 2000 L. El volumen de la etapa discontinua (arrancada) se definió igual a 1/3 del volumen total efectivo. Para la variante I, este volumen de arrancada se tomó como 1/3 del volumen efectivo de la primera etapa.

La concentración inicial de glucosa de 3 mM, garantiza que en la etapa discontinua se agote prácticamente toda la glucosa y al comenzar la etapa semicontinua sea menor su concentración. La concentración inicial de glucosa fue determinada por tanteo, a partir de simulaciones previas. La concentración de glutamina en el alimentado fue calculada a partir de la relación glutamina-glucosa, 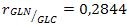, según [14].

Plataforma de diseño in silico

El programa MATLAB v.7.01 fue usado como plataforma para la simulación-optimización. La solución de las ecuaciones diferenciales ordinarias del modelo se realizó con la herramienta ode15s , recomendable para sistemas de ecuaciones diferenciales de escalas temporales variables (del tipo stiff en inglés). La optimización fue realizada con la herramienta patternsearch . Esta lleva a cabo un método eficaz de búsqueda directa de la región del óptimo. La programación se realizó según el modelo macroscópico para cada variante y se representaron gráficamente los resultados.

 

RESULTADOS Y DISCUSION

Optimización de la operación de la variante de simple etapa (Variante I)

Para esta variante se determinó que la máxima productividad en la síntesis de AcM que se alcanza es de 101,45 g año ^-1 L ^-1 , para un valor de D_E igual a 0,1355 d^-1 y una C_GA igual a 88,01 mM, (Figura 1). Se observa que en la región cercana al óptimo la sensibilidad para ambas variables es significativa. Las condiciones óptimas referidas para este caso permitirán comparar este sistema de cultivo con el de doble etapa.

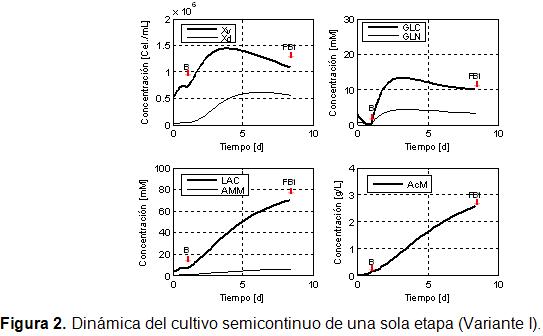
La concentración de células en estas condiciones alcanza un valor máximo de 1,4·10⁶ células/mL (Figura 2). Las fechas rojas indican la terminación de las etapas de propagación discontinua y fed-batch. La concentración celular alcanzada es baja, algo que puede estar asociado a la baja concentración del substrato limitante en el alimentado (88,01 mM).

La concentración máxima de AcM al final del proceso (Figura 2), muestra valores cercanos a 2,5 g/L, muy alto si se tiene en cuenta la baja concentración de biomasa lograda. Al comprar estos resultados con lo reportado [14], (1,2 g/L), se observa que son superiores en algo más que el doble, sin embargo, la concentración específica de AcM es semejante. Estos resultados son mejores que los reportados por el autor del modelo cinético [14], dado que en este trabajo se optimizaron más variables de diseño.

La dinámica del consumo de glucosa muestra, tal como se había dicho antes, que al terminar la etapa de arrancada, casi se agota este sustrato. Por otra parte, al comenzar la etapa semicontinua se comienzan a acumular los nutrientes, quedando al final de la fermentación una acumulación de glucosa de 10 mM y de glutamina de 3 mM.

La concentración máxima de lactato está en el orden de 70 mM, lo que sobrepasa los niveles nocivos para la célula, según estudios realizados [15]. Se ha demostrado que los efectos negativos del lactato se intensifican para valores superiores a 40 mM. El efecto negativo del amonio es observado desde niveles mucho más bajos de concentración, típicamente 2-4 mM, [15]. En las condiciones óptimas encontradas para esta variante I y a flujo constante, estas concentraciones permanece por encima de los límites permisibles.

Todo esto indica que el proceso optimizado, aunque con buenos resultados, posee limitaciones que de resolverse le otorgarían mayor potencial. Quizás una estrategia de alimentación con flujo variable sea más apropiada pero está fuera del alcance de este trabajo, enfocado más en hallar evidencias de lo que pudiera aportar un cultivo en dos etapas con objetivos diferentes, tesis planteada en trabajo precedente [18].

Optimización de la operación de la variante de dos etapas (Variante II)

En el caso de la variante de dos etapas, una variable muy importante es la fracción del volumen total del fermentador que sería destinada a cada etapa. Es por eso que se realizó el diseño óptimo de la operación variando la fracción de volumen de la primera etapa en el rango de 0 a 1. La Figura 3 evidencia que en la mayor parte de su intervalo, el aumento de esta variable produce una dependencia monótona creciente en la productividad. En los extremos, sin embargo, la productividad decrece bruscamente, sobre todo en el extremo superior. Este resultado resultó inicialmente sorprendente.

En busca de evidencias para explicar este comportamiento fue construida la Figura 4, que contiene los perfiles de concentración de las diferentes variables para una f_V igual a la unidad. Esto quiere decir que la primera etapa fue fed-batch y que la segunda etapa fue discontinua (batch), o sea, no se alimentan nutrientes. Este sería un caso extremo, próximo al estado en el que ocurre la inflexión en los extremos de la Figura 3, cuando f_V es casi la unidad. Nótese en la Figura 3 cómo, al comenzar la segunda etapa, las concentraciones de glucosa y glutamina caen bruscamente. En estas condiciones la concentración de biomasa viable es cercana a 1,2x10⁶ células/mL, lo que produce una demanda de nutrientes que no se puede satisfacer ante una baja disponibilidad de nutrientes en el tiempo restante. De aquí que los resultados en el extremo derecho de la Figura 3 se deben al desequilibrio que tal extremo genera entre demanda de nutrientes y su disponibilidad.

En el caso del extremo inferior izquierdo de la Figura 3, la explicación es semejante y viene dada por el efecto de dilución que se logra en la segunda etapa debido al desequilibrio entre la baja demanda de nutrientes basada en la cantidad mínima de células conseguidas en la primera etapa, debido al pequeño volumen de ésta.

Al calcular el aumento relativo de la productividad del cultivo en simple y en doble etapa (Figura 5) en función de la fracción de volumen f_V, se observa que para valores menores de 0,53 no se consigue un efecto positivo, o sea, no existe superioridad de la segunda variante.

La pregunta que surge ahora es: ¿cuál sería entonces el nivel óptimo de este factor? El factor socio-económico decide, en última instancia, la decisión que se tome. Hacia el futuro habría que plantearse la solución de este problema teniendo en cuenta la variable costo de producción o alguna otra relacionada con los indicadores de eficiencia de la inversión, si ese fuera el caso.

La función objetivo utilizada en este trabajo (productividad volumétrica), aunque tiene una estrecha relación con el desempeño económico del proceso, no siempre coincide con el óptimo de costo mínimo. Los autores consideran que la variable f_V requiere de una función objetivo de costo para una mejor precisión del diseño. Como el alcance de este trabajo solo llega hasta demostrar que hay diferencias entre las variantes de simple y doble etapa, entonces, para los fines de ilustración se escogió un valor de f_V de 80 %. Este valor garantiza una superioridad en productividad de un 30% de la variante II respecto a la variante I, tal como se ilustra en la Figura 5.

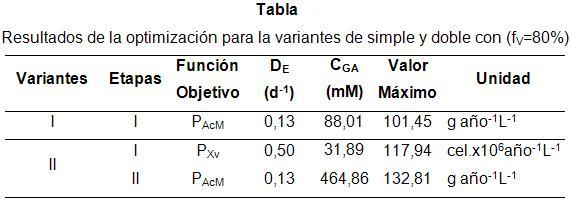
Las condiciones óptimas que se consiguen para f_V =80% junto con los resultados de la variante de simple etapa se muestran en la Tabla. Esta tabla muestra las grandes diferencias en los niveles óptimos de C_GA entre ambas variantes y entre la primera y segunda etapa de la variante de doble etapa (variante II).

Nótese las diferencias en las velocidades de dilución estática de la variante de dos etapas. Estas diferencias se deben a la función objetivo que fue utilizada para diseñarlas. Cuando la función objetivo fue maximizar la productividad de AcM, el valor de D_E debe ser 0,13 d^-1, sin importar el tipo de sistema de contacto. Sin embargo, cuando el objetivo es maximizar la productividad en biomasa, D_E debe ser de 0,5 d^-1. Este resultado coincide con las predicciones realizadas por los autores en el trabajo anterior [18]: altas velocidades de dilución favorecen la formación de biomasa y bajas favorecerán la producción del AcM.

La Figura 6 evidencia que en la región cercana al óptimo existe poca sensibilidad de la productividad cuando cambian los valores de las variables estudiadas. Se comporta como si apareciera una saturación del proceso que no produce inhibición, pero que tampoco permite mejorar el desempeño del proceso. Este comportamiento sería muy interesante desde el punto de vista del costo de operación, pues tendería a producir un mínimo a partir del máximo de productividad alcanzado.

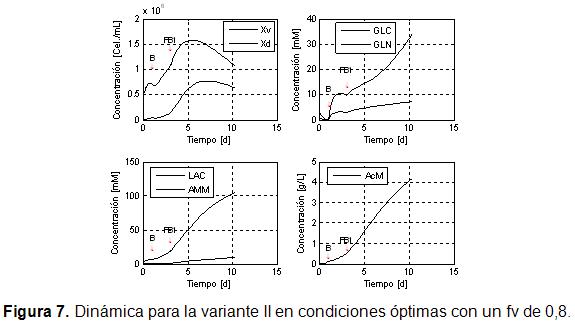
Los resultados de la simulación del comportamiento de la dinámica del sistema en dos etapas, en las condiciones óptimas (Tabla), para una fv de 0,8 (Figura 7), indican que la concentración de células viables alcanza en la primera etapa un valor de células/mL. Esta concentración, aunque aún baja, cuando se compara con lo alcanzado en la variante de simple etapa resulta superior en un 21,43%. La concentración del AcM al finalizar el proceso alcanza un nivel de 4,1 g/L. Este valor es un 58 % mayor que el valor máximo alcanzado en la variante de simple etapa, lo que demuestra la mejora lograda con la estrategia de cultivo en doble etapa.

Las concentraciones de glucosa y glutamina se acumulan a más del doble en comparación con la variante de simple etapa, mientras que las de lactato y las de amonio están muy por encima de los rangos reportados en la literatura como nocivos para el crecimiento celular. Estos resultados indican que el cultivo en doble etapa con flujo constante no resuelve tampoco la acumulación de estas sustancias nocivas para la célula. A pesar de esto se logra una mejoría notable del proceso en cuanto a productividad. Estas condiciones de nocividad no provocan un cambio significativo en la sensibilidad del proceso según se observa en la Figura 6.

Análisis comparativo de los parámetros operativos de cada variante

Según se ha reportado [18], las condiciones que favorecen el aumento de la productividad de AcM son aquellas que garantizan que en la primera etapa sea máxima la velocidad específica de crecimiento para elevar la productividad en biomasa y una segunda etapa que tenga alta la concentración de biomasa y baja velocidad específica de crecimiento.

En la Figura 7 se puede observar la dinámica para la variante II en condiciones óptimas con un fv de 0,8.

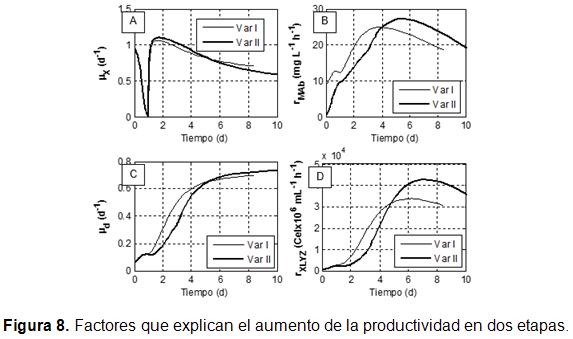
La Figura 8 contiene las evidencias que explican las causas de los mejores resultados obtenidos en la optimización y la coincidencia con lo antes predicho [15]. En la variante II, la velocidad específica de crecimiento (Figura 8 A) es superior en su primera etapa, situada entre el tercero y el quinto día, comparada con el sistema de simple etapa (variante I). Esto explica por qué se alcanza una mayor concentración de biomasa en esta primera etapa que la conseguida en todo el sistema de simple etapa.

Al pasar a la segunda fase de la variante II, esta variable cae por debajo de la variante I, produciendo mejores condiciones para producir mayor cantidad de AcM [18]. Estas observaciones se reflejan en la velocidad de producción del AcM (Figura 8 B), que pasa a ser superior en la variante de doble etapa sólo al entrar a su última fase. La velocidad específica de muerte celular ( Figura 8 C) y la velocidad de lisis celular (Figura 8 D) confirman la particularidad del escenario productivo creado en la variante II, favorable a una mayor productividad en el AcM. En la primera etapa de la variante II ambas variables están por debajo de la variante I, lo que permite lograr el aumento de biomasa y luego en la segunda etapa, estas variables empeoran respecto a la variante I. Este cambio de escenario tiene como causa que el proceso en esta fase ya no prioriza maximizar la biomasa sino la síntesis de AcM. Los resultados indican que el incremento en productividad conseguido es significativo con una modificación tan simple del proceso, consistente en operar con dos flujos en el cultivo fed-batch.

Queda pendiente para próximos trabajos diseñar el proceso de doble etapa pero en operación continua con perfusión.

En la figura 8, Var I se refiere al proceso en simple etapa y Var II se refiere al proceso en doble etapa.

 

CONCLUSIONES

Se demostró que un sistema de cultivo semicontinuo en dos etapas consigue incrementos significativos de la productividad de AcM respecto a uno de simple etapa. Las simulaciones realizadas en estos sistemas de cultivo de volumen variable con alimentación de flujo constante, padecen de la deficiencia de acumular sustancias nocivas en el medio y de mantener altos niveles de los sustratos al finalizar el proceso, algo que incluso empeora para doble etapa. Otros sistemas de cultivo en doble etapa pudieran mitigar estos efectos y así se conseguiría una mejora aún más notable.

 

NOMENCLATURA

µ d- Velocidad específica de células muertas (h^-1)

µ máx- Velocidad específica de crecimiento máxima (h^-1)

µ X- Velocidad específica de crecimiento (h^-1)

AcM- Concentración de anticuerpo monoclonal (mg/L)

AcM_f - Concentración de anticuerpo monoclonal final (mg/L)

AMN- Concentración de amonio (mM)

D_D - Velocidad de dilución dinámica (d^-1 )

D_E - Velocidad de dilución estática (d^-1 )

GLC- Concentración de glucosa (mM)

GLN- Concentración de glutamina (mM)

GLC f - Concentración de glucosa en el alimentado (mM)

GLN f - Concentración de glutamina en el alimentado (mM)

LAC- Concentración de lactato (mM)

n_ca - Números de ciclos anuales

P_a - Productividad anual de anticuerpo monoclonal (mg/año L)

P_XV - Productividad anual en biomasa (células /año L)

r_AcM - Velocidad de producción de anticuerpo monoclonal (mM/h)

r_AMN - Velocidad de producción de amonio (mM/h)

r_GLC - Velocidad total de consumo de glucosa (mM/h)

r_GLN - Velocidad total de consumo de glutamina (mM/h)

r_LAC - Velocidad de producción de lactato (mM/h)

r_Xd- Velocidad de síntesis de células muertas (mM/h)

r_XLYZ - Velocidad de lisis de las células muertas (células.10⁶ /mL h)

r_XV- velocidad de síntesis de células viables (mM/h)

Xd-Concentración de células muertas (células/mL)

Xv- Concentración de células viables (células/mL)

Xvf- Concentración de células viables final (células/mL)

 

BIBLIOGRAFIA

1. AMABLE, P.,BUTLER, M. "Cell metabolism and its control in culture". Animal Cell Technology: From Biopharmaceuticals to Gene Therapy. UK:Taylor & Francis Group, 2008. p. 75-110.

2. AMRIBT, Z., et al. "Macroscopic modelling of overflow metabolism and model based optimization of hybridoma cell fed-batch cultures". Biochemical Engineering Journal. 2013, Vol.70, p. 196–209.

3. BERRIOS, J., et al. "Continuous CHO cell cultures with improved recombinant protein productivity by using mannose as carbon source: Metabolic analysis and scale-up simulation". Chemical Engineering Science. 2011, Vol.66, p. 2431-2439.

4. CHICO, E. "Technological challenges for a better accessibility of immunotherapeutics". Biomanufacturing challenges of immunotherapy, La Habana, Cuba, 2013.

5. CHICO, E., et al. "Bioreactors for animal cells". Animal Cell Technology: From Biopharmaceuticals to Gene Therapy.New York and Abingdon:Taylor & Francis Group, 2008. p. 221-258.

6. DEY, S., et al. "Fermenter balancing for semi-continuous, multi-tank mammalian cell culture processes". Chemical Engineering Journal. 1997, Vol.65, p. 123-132.

7. ELVIN, J. G., et al. "Therapeutic antibodies: Market considerations, disease targets and bioprocessing". International Journal of Pharmaceutics. 2013, Vol.440, p. 83-98.

8. FENGE, C., LÜLLAU, E. "Cell culture bioreactors". Cell culture technology for pharmaceutical and cell based therapies.United States of America:Taylor & Francis Group, 2006. p. 155-224.

9. FONTANET, L., et al. "La excelencia operacional en la industria biotecnológica. Una aproximación desde las operaciones industriales del CIM". Bioprocesos. 2011.

10. GERNAEY, K., GANI, R. "A model-based systems approach to pharmaceutical product-process design and analysis". Chemical Engineering Science. 2010, Vol.65, p. 5757-5769.

11. GÓMEZ, L. G.,VILLALOBOS, M. A. "Ajuste de modelos cinéticos en el proceso de producción del anticuerpo monoclonal Nimotuzumab". Departamento de Ingeniería Química, 2014, p. 63.

12. GONZALEZ, L. M. "Evaluación del desempeño técnico económico y ambiental de la producción de Nimotuzumab en el Centro de Inmunología Molecular". Departamento de Ingeniería Química, 2014, 73 p.

13. HO, Y., et al. "Computational approach for understanding and improving GS-NS0 antibody production under hyperosmotic conditions". Journal of Bioscience and Bioengineering. 2012, Vol.113, p. 88-98.

14. KIPARISSIDES, A., et al. "Closing the loop in biological systems modeling. From the in silico to the in vitro". Automatica. 2011, Vol.47, p. 1147-1155.

15. KOMPALA, D. S., OZTURK, S. S. "Optimization of high cell density perfusion bioreactors". Cell Culture Technology for Pharmaceutical and Cell-based.United States of America:Taylor & Francis Group, 2006. p. 387-416.

16. LAM, C., et al. "Cell Cycle Modelling for Off-line Dynamic Optimisation of Mammalian Cultures". 18th European Symposium on Computer Aided Process Engineering-ESCAPE 18, 2008.

17. POTVIN, G., et al. "Bioprocess engineering aspects of heterologous protein production in Pichia pastoris: A review". Biochemical Engineering Journal. 2012, Vol.64, p. 91-105.

18. SÁNCHEZ, H., et al. "Use of selectivity factor on cell-culture systems conceptual design". Biotecnología Aplicada. 2016, Vol.2. num 3, p. 3301-3306.

19. WEBER, W., et al. "A genetic redox sensor for mammalian cells". Metabolic Engineering. 2006,Vol.8, p. 273-280.

20. ZADEH, K. "A synergic simulation-optimization approach for analyzing biomolecular dynamics in living organisms". Computers in Biology and Medicine. 2011, Vol.41, p. 24-36.

 

 

Recibido: Noviembre 2016
Aprobado: Marzo 2017

 

 

Dr.C. Luis B. Ramos-Sánchez. Departamento de Ingeniería Química. Universidad de Camagüey "Ignacio Agramonte Loynaz". Camagüey. Cuba. [e-mail]