ARTICULO ORIGINAL

 

 

EMPLEO DEL MATLAB EN LAS CLASES PRÁCTICAS DEL TEMA 2 DE MICROBIOLOGÍA PARA INGENIERÍA QUÍMICA

 

USING MATLAB IN PRACTICAL LESSONS OF THE TOPIC 2 OF MICROBIOLOGY FOR CHEMICAL ENGINEERING

 

 

MSc. Dunia Rodríguez Heredia 1 , MSc. Henry Bory Prevez 2

1 Facultad de Ingeniería Química y Agronomía, Universidad de Oriente, Santiago de Cuba, Cuba. [e-mail]
2 Facultad de Ingeniería Eléctrica, Universidad de Oriente, Santiago de Cuba, Cuba. [e-mail]

 

 

---

Resumen

Las clases prácticas del tema 2 de Microbiología para Ingeniería Química están relacionadas con la construcción de curvas de crecimiento microbiano, el análisis de la influencia de factores físicos y químicos en el crecimiento y el cálculo de parámetros cinéticos. En estas actividades docentes el estudiante debe graficar varias veces para solucionar los ejercicios planteados. Teniendo en cuenta lo anterior y el hecho de que la educación superior cubana plantea la necesidad de que cada asignatura tenga asociado un programa computacional, se plantea como objetivo emplear el MatLab como asistente matemático en la resolución de los ejercicios de las clases prácticas del Tema 2 “Fisiología de los microorganismos” de la asignatura Microbiología. Se exponen tres de los ejercicios a resolver en estas clases prácticas, se presenta la forma en que se resolverían empleando el MatLab, y por último las ventajas que supone trabajar en la asignatura con este programa profesional. Se concluye que se vincula la asignatura con el programa director de computación a la vez que se emplea un lenguaje de programación nuevo para los estudiantes que les sirve de base para el Control de Procesos Químicos.

Palabras Clave : Microbiología, Ingeniería Química, MatLab.

---

Abstract

The practical lessons of topic 2 of Microbiology for Chemical Engineering are related to the construction of microbial growth curves, the analysis of the influence of physical and chemical factors on growth and the calculation of kinetic parameters. In these teaching activities the student must graph several times to solve the exercises. Taking into account the above and the fact that cuban superior education requires that each subject has associated a computer program, the objective is to use MatLab as a mathematical assistant in solving the exercises of the practical lessons of topic 2 "Physiology of microorganisms" of the subject Microbiology. Three of the exercises to solve in these practical lessons are exposed, the way in which they would be solved using the MatLab is presented, and finally the advantages of working in the subject with this professional program. It is concluded that the subject is linked to the computer director program while using a programming language new for the students that serves as basis for the Control of Chemical Processes.

Keywords : Microbiology, Chemical Engineering, MatLab.

---

 

 

INTRODUCCION

La asignatura Microbiología es básica específica y se imparte en el tercer año de la carrera Ingeniería Química, para familiarizar al estudiante con los procesos industriales mediados por microorganismos (m.o.), de ahí su papel en el plan de estudios, ya que el futuro egresado de la carrera estaría capacitado para operar en plantas en las que se lleven a cabo procesos fermentativos como en las industrias láctea, cervecera, de vinos y licores, también en fábricas de conservas de frutas y vegetales, así como en procesos biotecnológicos, todos muy comunes en la región oriental del país.

Es por lo anterior que en la asignatura se imparten contenidos relacionados con la cinética del crecimiento microbiano, genética microbiana y microbiología de los alimentos, por solo mencionar algunos.

Para que el estudiante se apropie del contenido, se imparten, entre otras formas de docencia, las clases prácticas, en muchas de las cuales los estudiantes se tienen que enfrentar al graficado de curvas, procesamiento matemático de los datos, aspectos que consumen gran cantidad de tiempo, quedando poco para un análisis y discusión más amplia de los resultados. Otra dificultad es que no se pueden poner ejercicios que impliquen gran volumen de datos porque se consumiría todo el tiempo sólo en el procesamiento y graficado de estos.

Teniendo en cuenta lo anterior y el hecho de que una de las estrategias curriculares de la enseñanza superior cubana es la estrategia de computación, en la cual todas las asignaturas deben tener asociados programas computacionales, se plantea como objetivo de este trabajo: emplear el MatLab como asistente matemático en la resolución de los ejercicios de las clases prácticas del Tema 2 “Fisiología de los microorganismos” de la asignatura Microbiología.

 

FUNDAMENTACIÓN TEÓRICA

En el plan de estudios de la carrera Ingeniería Química, se imparte la asignatura Microbiología, para dotar a los futuros egresados de los conocimientos que les permitan operar en plantas en las que se llevan a cabo procesos mediados por microorganismos, o en las que haya que controlar la calidad microbiológica de materia prima, proceso y producto, por ser susceptibles al ataque microbiano, como ocurre en las industrias de alimentos [1].

Para que el estudiante se apropie del contenido de la asignatura, esta se imparte en cuatro formas de docencia: conferencias, clases prácticas, seminarios y laboratorios. Las clases prácticas están distribuidas entre los temas 2 “Fisiología de los microorganismos” y 3 “Genética y Microbiología ambiental y aplicada”, y se han diseñado de forma tal que los estudiantes aprendan a resolver problemas relacionados con el crecimiento microbiano, el cálculo de parámetros cinéticos, el cálculo del rendimiento, así como relacionados con la influencia de factores físicos y químicos en el crecimiento [2].

En la clase práctica 1: “Construcción de curvas de crecimiento microbiano”, perteneciente al tema 2 de la asignatura, los estudiantes se enfrentan a números muy grandes y a gran volumen de datos, lo cual no es de extrañar pues se trata del crecimiento exponencial de los microorganismos. Hasta la fecha, esta clase práctica se imparte en el aula, y los estudiantes deben graficar varias curvas con muchos datos a procesar, por lo que sería conveniente emplear un programa computacional que permita graficar de igual manera, pero a su vez, que contribuya a desarrollar en los estudiantes la habilidad de algoritmizar, la cual es útil en el pregrado para la programación y porque imprime mayor velocidad a la solución de los ejercicios, pero además es también importante en la práctica profesional.

Si bien el Excel es el procesador de datos por excelencia, no fomenta en los estudiantes las habilidades de la programación, por lo cual se sugiere se emplee el MatLab como herramienta computacional para la solución de los ejercicios de las clases prácticas del tema 2 de la asignatura.

En la carrera de Ingeniería Química de la Universidad de Oriente no se utiliza el MatLab como herramienta computacional, sin embargo, hay trabajos [3-7] donde se reporta el empleo de este por los múltiples usos que se le adjudican, ya sea en la carrera de Ingeniería Química o en carreras afines, para el control de procesos químicos debido a la facilidad que brinda el MatLab para el desarrollo de algoritmos con los cuales se puede simular el control de procesos químicos complejos.

Hay autores [3] que dan cuenta de la utilidad metodológica de herramientas de software a la docencia y la investigación y apuestan por el MatLab como una de las herramientas más extendidas en la Ingeniería de Control. Otros autores [4] recomiendan el empleo del MatLab para el graficado y modelación con regresión lineal para predecir y conocer el comportamiento de la vida útil de varias marcas de leche pasteurizada a diferentes condiciones de temperatura. Esta experiencia se llevó a cabo en el laboratorio de microbiología de la carrera Ingeniería de Procesos en la Universidad Mariana, Colombia, vinculándose la docencia con la práctica profesional.

También se ha utilizado el MatLab en el desarrollo de una herramienta para obtener el índice de control microbiológico de la línea de producción de jugos gaseosos llenados en frío [5]; y como núcleo de una estrategia de aprendizaje activo en la cual los estudiantes deben desarrollar un programa en MatLab que les permita balancear ecuaciones químicas mediante el método algebraico [6].

Si bien los mencionados artículos dan cuenta del uso del MatLab en Ingeniería Química y en otras carreras afines, el trabajo presentado en [7] engloba los posibles usos de esta herramienta computacional en todas las asignaturas de esta carrera. Estos autores argumentan que para la adquisición adecuada de las competencias básicas que debe poseer un graduado en Ingeniería Química es necesario el uso de paquetes de software numérico de propósito general, como MatLab , destinados a la simulación estacionaria y dinámica de procesos. Se propusieron emplear este software como nexo de unión entre las asignaturas de la carrera argumentando que, por lo general, en las diferentes asignaturas se emplean disímiles software, lo que propicia que el estudiante sepa un poco de cada uno pero no profundice. Se plantearon implicar a todos los profesores de las diferentes asignaturas de la carrera, incluyendo las asignaturas básicas como la Física, en la utilización de MatLab como único software matemático. Además, en este trabajo se exponen con claridad las razones por las cuales se consideró MatLab como el software matemático más adecuado a utilizar en Ingeniería Química, sin dejar de utilizar otros programas como el Excel.

Los autores mencionados, así como otros trabajos presentados [8] y [9] coinciden en que las bondades del MatLab como lenguaje de programación son, entre otras, las siguientes: a mplio soporte matemático, alta precisión, amplio soporte de funciones ya desarrolladas, magnífica ayuda y gráficas bidimensionales y tridimensionales de diferentes tipos, además de ser un lenguaje de alto nivel para el cálculo numérico/simbólico empleado en el ámbito científico e ingenieril, tanto a nivel académico como industrial para el análisis, diseño y simulación de procesos dinámicos de tiempo continuo, de tiempo discreto y de eventos discretos.

MATERIALES Y MÉTODOS

A continuación, se presentan tres de los ejercicios de la asignatura Microbiología, que se deben resolver en las clases prácticas del tema 2. Estos han sido tomados y adaptados de las bibliografías [10] y [11].

Los ejercicios 1 y 2 pertenecen a la clase práctica 1, y el ejercicio 3 a la clase práctica 2.

Ejercicio 1 : Construya las curvas de logaritmo de supervivientes por mL contra el tiempo de exposición en minutos, para cada temperatura, cuando se emplea como microorganismo la Escherichia coli y una concentración de fenol de 4,62 g/L a partir de los datos mostrados en la Tabla 1.

 

a) Cómo influye la temperatura en la destrucción de los m.o. sometidos a la acción del agente germicida?

b) Si tuviera que utilizar una concentración de fenol más alta, ¿pudiera utilizarse una temperatura más baja? Explique.

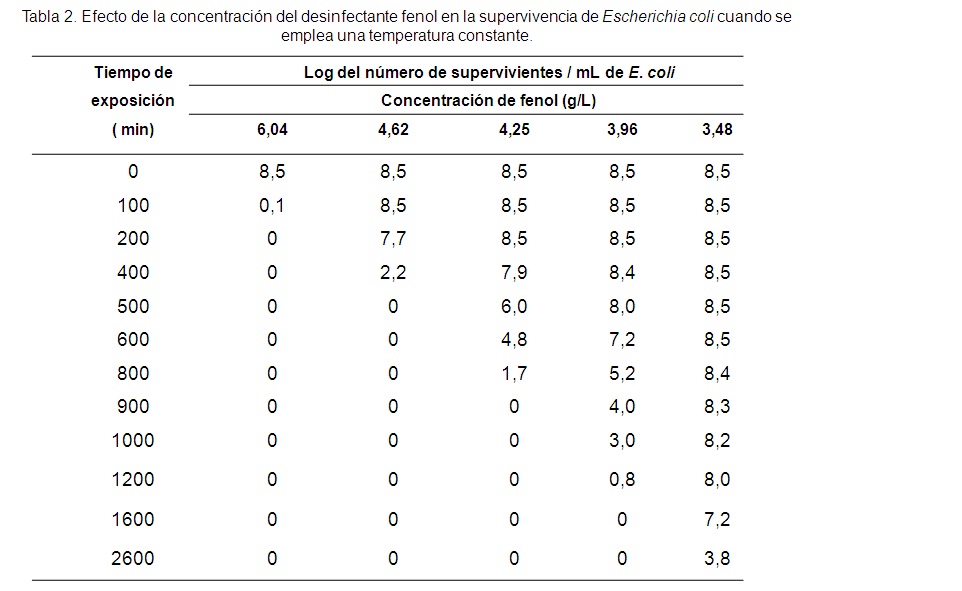
Ejercicio 2 : Durante un estudio para analizar la influencia de la concentración de fenol sobre la supervivencia de Escherichia coli en un laboratorio, se obtuvieron los resultados mostrados en la Tabla 2, a temperatura constante de 35 °C.

 

a)  Construya las curvas de logaritmo de supervivientes contra tiempo de exposición para cada concentración de fenol.

b) Diga a qué concentración es más efectivo el agente en menos tiempo.

c)  ¿Qué implicación tiene sobre el costo, la utilización de la concentración más alta de fenol?

Ejercicio 3 : Los datos de la fase exponencial de crecimiento de tres especies bacterianas que utilizan glucosa como fuente de carbono son mostrados en la Tabla 3. Indique cual de las tres especies crecerá más rápidamente.

RESULTADOS Y DISCUSIÓN

En este acápite se presenta la forma en que, programando en MatLab, se resuelven los ejercicios planteados anteriormente.

Solución del Ejercicio 1:

Lo primero que debe hacer el estudiante según la orientación del ejercicio es graficar los datos, ¿cómo hacerlo empleando MatLab? Lo primero es entrar los datos creando las variables, correspondientes en este caso a cada temperatura, lo cual debe hacerse creando vectores, llamados arreglos unidimensionales en otros lenguajes de programación, siguiendo la sintaxis nombrevariable=[número1 número 2 … númeron] como se muestra a continuación. Importante, en MatLab debe usarse punto para separar la parte entera de la decimal y punto y coma si el usuario no desea ver la operación en pantalla.

En este ejercicio se definieron las variables texp, moT42, moT35 y moT30 para almacenar los valores de los tiempos de exposición y de los logaritmos de supervivientes a las diferentes temperaturas.

 

%Area definición de variables.
texp=[0 100 200 400 600 800 1000 2000];
moT42=[8.5 0.5 0 0 0 0 0 0];
moT35=[8.5 8.5 8.2 3.0 0 0 0 0];
moT30=[8.5 8.5 8.5 8.5 8.3 8.1 7.8 1.98];
%Fin área definición de variables.
El símbolo % se usa para comentarios que el programador desee documentar.

Una vez definidas las variables, se emplea la instrucción plot para crear la gráfica con las diferentes curvas, la cual posee la siguiente sintaxis:

plot(variableindependiente,variabledependiente,'estilodelgráfico')

como se muestra a continuación:

plot(texp,moT42, 'k^-' ,texp,moT35, 'ko--' ,texp,moT30, 'kv-.' ), ...
grid, ... % Adiciona rejilla al gráfico
legend( 'm.o. 42 °C' , 'm.o. 35 °C' , 'm.o. 30 °C' ), ... % Adiciona leyenda al gráfico
xlabel( 'Tiempo de exposición (min.)' ), ... % Adiciona título al eje X del gráfico
ylabel( 'log(# supervivientes/mL)' ), ... % Adiciona título al eje Y del gráfico
title( 'Gráfica log(# supervivientes/mL) v.s. tiempo a diferentes temperaturas' ) % Título

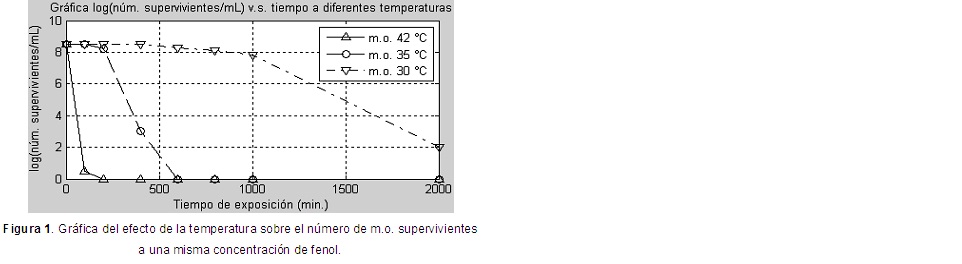
Luego de ejecutadas las instrucciones anteriores, se obtiene el gráfico mostrado en la Figura 1.

Una vez obtenido el gráfico, el estudiante, al interpretarlo, puede responder los incisos a) y b) y llegar a la conclusión que a una misma concentración del agente químico, un aumento de la temperatura (agente físico) provoca una destrucción más rápida del microorganismo.

Solución del Ejercicio 2:

Lo primero que debe hacer el estudiante, como en el ejercicio anterior es graficar los datos para lo cual puede crear un programa similar al anterior, quedando de la siguiente forma:

%Area definición de variables.
texp=[0 100 200 400 500 600 800 900 1000 1200 1600 2600];
ConcFe604=[8.5 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0];
ConcFe462=[8.5 8.5 7.7 2.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0];
ConcFe425=[8.5 8.5 8.5 7.9 6.0 4.8 1.7 0.0 0.0 0.0 0.0 0.0];
ConcFe396=[8.5 8.5 8.5 8.4 8.0 7.2 5.2 4.0 3.0 0.8 0.0 0.0];
ConcFe348=[8.5 8.5 8.5 8.5 8.5 8.5 8.4 8.3 8.2 8.0 7.2 3.8];
%Fin área definición de variables.
%Area de graficado de datos.
plot(texp,ConcFe604, 'k^-' ,texp,ConcFe462, 'ko-' ,texp,ConcFe425, 'kv-' , ...
texp,ConcFe396, 'kd-' ,texp,ConcFe348, 'kp-' ), ...
grid, ...
legend( 'Conc. Fenol 6.04 g/L' , 'Conc. Fenol 4.62 g/L' , 'Conc. Fenol 4.25 g/L' , ...
'Conc. Fenol 3.96 g/L' , 'Conc. Fenol 3.48 g/L' ), ...
xlabel( 'Tiempo de exposición (min.)' ), ...
ylabel( 'log(núm. supervivientes/mL)' ), ...
title( 'Gráfica log(núm. supervivientes/mL) v.s. tiempo a diferentes Conc. Fenol' )

Luego de ejecutar estas instrucciones se obtiene el gráfico de la Figura 2.

 

Al igual que en el ejercicio anterior, la obtención del gráfico es vital para responder los otros incisos del ejercicio, los cuales poseen un enfoque similar a los incisos del ejercicio 1.

Solución del Ejercicio 3:

A diferencia de los ejercicios anteriores, en los cuales en una misma gráfica eran mostradas las diferentes curvas, en este caso es conveniente tener tres gráficos diferentes en una misma ventana de figura. Esto se logra empleando la instrucción subplot(f,c,g), en la cual f y c son el número de filas y columnas en que se divide la ventana de figura y g es el número del gráfico en el que se graficará la curva.

% Especie A
tA=[4:1:8];
LogNA=[4.64 4.81 4.98 5.15 5.32];
% Especie B
tB=[3:1:7];
LogNB=[5.30 5.44 5.58 5.72 5.86];
% Especie C
tC=[5:1:9];
LogNC=[6.22 6.37 6.52 6.67 6.82];
%Area de graficado de datos.
subplot(1,3,1), ...
plot(tA,LogNA, 'k-' ), ...
grid, ...
xlabel( 'Tiempo (h)' ), ...
ylabel( 'log(# m.o. especie A)' ), ...
subplot(1,3,2), ...
plot(tB,LogNB, 'k-' ), ...
grid, ...
title( 'Gráfica log(# m.o.) v.s. tiempo para diferentes especies' ), ...
xlabel( 'Tiempo (h)' ), ...
ylabel( 'log(# m.o. especie B)' ), ...
subplot(1,3,3), ...
plot(tC,LogNC, 'k-' ), ...
grid, ...
xlabel( 'Tiempo (h)' ), ...
ylabel( 'log(# m.o. especie C)' ), ...
%Fin área de graficado de datos.

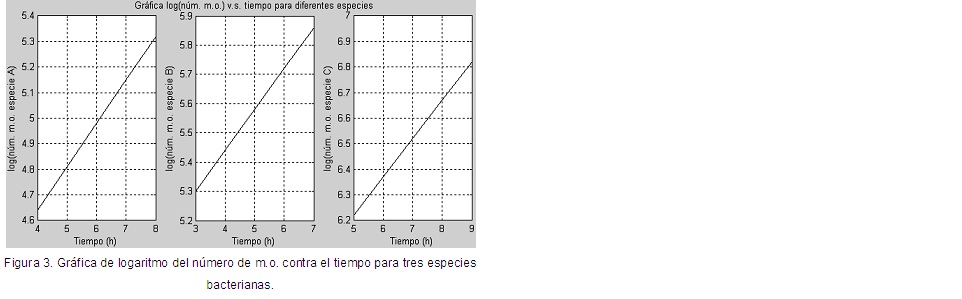
Luego de ejecutar estas instrucciones se obtiene el gráfico de la Figura 3.

Para conocer cuál de las tres especies crecerá más rápidamente, se debe calcular la pendiente de cada recta, la cual se corresponde con la velocidad específica de crecimiento. También hay que calcular el tiempo de generación para saber cuál especie se divide más rápido en el tiempo.

% Especie A
mA=(LogNA(end)-LogNA(1))/(tA(end)-tA(1))*2.303;
gA=log(2)/mA;
%Especie B
mB=(LogNB(end)-LogNB(1))/(tB(end)-tB(1))*2.303;
gB=log(2)/mB;
%Especie C
mC=(LogNC(end)-LogNC(1))/(tC(end)-tC(1))*2.303;
gC=log(2)/mC;

Para presentar los resultados de los cálculos anteriores de forma ordenada en pantalla se emplea la instrucción fprintf, como se ejemplifica a continuación:

fprintf( ' Los parámetros de las especies son: \n' )
fprintf( '----------------------------------------- \n' )
fprintf( ' Especie A Especie B Especie C \n' )
fprintf( '----------------------------------------- \n' )
fprintf( 'miu=' )
fprintf( '%8.2f 1/h' ,mA,mB,mC)
fprintf( '\n' )
fprintf( ' g=' )
fprintf( '%8.2f h' ,gA,gB,gC)
fprintf( '\n' )
fprintf( '----------------------------------------- \n' )

 

El resultado de ejecutar las instrucciones anteriores es:

Los parámetros de las especies son:

----------------------------------

Especie A Especie B Especie C

----------------------------------
miu= 0.39 1/h 0.32 1/h 0.35 1/h
g= 1.77 h 2.15 h 2.01 h
----------------------------------

Como se observa, la instrucción fprintf permite visualizar en pantalla tanto carteles como los valores numéricos de las variables.

De todo lo anterior se puede apreciar que teniendo un primer ejercicio programado, el estudiante solo tendría que adecuar el resto de los ejercicios a la problemática en particular, por cuanto las formas de preguntar son semejantes.

De aplicar la propuesta que se hace en este trabajo, cambiaría el diseño de las clases prácticas, pues hasta la fecha solo se realizan tres clases prácticas en el tema 2, la primera de construcción de curvas de crecimiento microbiano, y las otras de cálculo de parámetros cinéticos. Con este nuevo enfoque, se propondrían cuatro clases prácticas del tema, en la primera y la segunda se resolverían ejercicios tipo de curva de crecimiento y de cálculo, respectivamente, y en la tercera y cuarta, ejercicios de las mismas temáticas, pero más complejos, con datos reales, por lo que se realizarían empleando MatLab, y se llevarían a cabo en el laboratorio de computación. Al aumentar una clase práctica se afianza el conocimiento del estudiante en el tema, lo que se traduce en una mayor ejercitación para la realización de la Prueba Parcial 1.

Entre las múltiples ventajas que se obtendrían de emplear el MatLab en la solución de los ejercicios de las clases prácticas del tema 2, se presentan:

•  Las clases prácticas pudieran incluir más ejercicios del mismo tipo, ya que con la ayuda del procesador computacional se aumentaría la velocidad de resolución de los ejercicios. Esto se traduce en una mayor ejercitación del tema y mayor adquisición de los conocimientos por parte de los estudiantes.

•  Se emplea otro lenguaje de programación, MatLab, el cual, hasta la actualidad no se emplea en la carrera.

•  Los estudiantes se apropian de la forma en la que se programa en el MatLab, lenguaje de programación nuevo para ellos, por lo que amplían su cultura y consolidan el método en que los ingenieros resuelven los problemas de la vida real, empleando herramientas matemáticas.

•  Se pone al descubierto cómo la asignatura contribuye al plan de desarrollo de computación ya que las dos últimas clases prácticas del tema contendrían ejercicios a resolver empleando MatLab, por lo que se llevarían a cabo en un laboratorio de computación.

•  Aumentaría el interés de los estudiantes para generalizar conceptos e incluso ampliar los desarrollos de software en MatLab para abordar problemas más complejos que los propuestos en clase.

•  Como el entorno de MatLab está en idioma inglés, se contribuiría a fomentar la estrategia de enseñanza del inglés.

CONCLUSIONES

En este artículo se mostró la utilidad del MatLab para la realización de los ejercicios de las clases prácticas del Tema 2 “Fisiología de los microorganismos” de la asignatura Microbiología para Ingeniería Química . Dentro de las ventajas que supone lo anterior están que se vincula la asignatura con el programa director de computación a la vez que se emplea un lenguaje de programación nuevo para los estudiantes que les sirve de base para la solución de problemas profesionales.

BIBLIOGRAFÍA

1)  Comisión Nacional de Carrera de Ingeniería Química. Plan de Estudios D modificado, carrera Ingeniería Química. Universidad de Oriente, 2010.

2)  FIQA. Programa Analítico de la asignatura Microbiología, carrera Ingeniería Química, curso 2016-2017.

3)  FERNÁNDEZ, E, et al. “Desarrollo de software en Comproductive Control y Matlab para asignaturas de Control en Ingeniería Química”. [ref. de 20 de noviembre 2017]. Disponible en Web: https://web.ua.es/va/ice/jornadas-redes-2015/documentos/tema-2/410859.pdf

4)  GARCÍA, Juliana, et al. “Evaluación del efecto de temperatura, tiempo, pH y UFC, sobre la vida útil de leche pasteurizada en marcas comercializadoras en Pasto (Nariño)”. Revista Biumar . 2017, vol 1, núm. 1, p. 46-58.

5)  ESCOBAR CRUZ, Diana María. “Diseño de un sistema indicador para el comportamiento microbiológico de una línea de producción de jugos de llenado en frío”. Director: Ligia Consuelo Sánchez. Universidad de La Sabana, Facultad de Ingeniería, 2011.

6)  REGALADO, Alejandro, et al. “Balanceo de ecuaciones químicas integrando las asignaturas de química general, algebra lineal y computación: un enfoque de aprendizaje activo”. Formación Universitaria . 2014, vol 7, núm. 2, p. 29-40.

7)  LÓPEZ, María Fernanda, et al. Resultados del Proyecto de Innovación y Mejora Educativa. Utilización de MATLAB como estrategia didáctica y de coordinación horizontal y vertical entre asignaturas del Grado de Ingeniería Química [en línea] . Universidad Politécnica de Valencia. 2015. [ref. de 20 de octubre 2017]. Disponible en Web: http://dx.doi.org/10.4995/INRED2015.2015.1567

8)  BORY, Henry, et al. “Empleo del Simulink del MatLab para la simulación de Bioreactores”. Revista Tecnología Química . 2009, vol XXIX, núm. 1, p. 43-50.

9)  SÁNCHEZ, Carlos. Curso de utilización práctica de Matlab [en línea]. 2006. p. 1-203. [ref. de 20 de octubre 2017]. Disponible en Web: http://biocomp.cnb.csic.es/~coss/Docencia/MATLAB/ApuntesGrande.pdf

10) PELCZAR, Michael, et al. Microbiología. Hontañón, Leopoldo (Trad. y adapt.); Pelczar, Michael (prol.). 1a ed. Ciudad de la Habana: Pueblo y Educación, 1979. 664 p.

11) ARANA, Inés, et al. “Cómo abordar y resolver aspectos prácticos de Microbiología”. [ref. de 20 de noviembre 2017]. Disponible en Web: https://ocw.ehu.eus/file.php/48/Tema_4._calculo_de_los_parametros_que_definen_el_crecimiento_bacteriano.pdf

 

 

Recibido: Noviembre 2017
Aprobado: Marzo 2018

MSc. Dunia Rodríguez Heredia. Facultad de Ingeniería Química y Agronomía, Universidad de Oriente, Santiago de Cuba, Cuba.