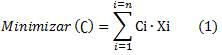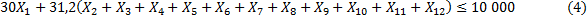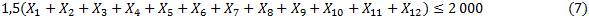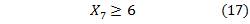Introducción
La economía cubana por sus recursos limitados, necesita ser cada día más eficiente y competitiva, para insertarse en los mercados globalizados del mundo y poder alcanzar los niveles de utilidades que desea el país. Es por ello que el aumento de las ganancias de las empresas, como resultado de un elevado nivel de calidad y variedad de los productos junto con una disminución de los costos, debe ser un objetivo a alcanzar por cada una de ellas.
La producción de helados utiliza una de las tecnologías de mayor consumo energético y de materias primas, los cuales implican un alto costo, por lo que es necesaria la búsqueda de estrategias para disminuir las pérdidas y los costos de producción realizando variaciones en el proceso con el objetivo de disminuir al máximo las deficiencias del mismo, de manera que se pueda aumentar la competitividad.
La fábrica de helados Alondra cita en el Zoológico Nacional, Boyeros, La Habana, Cuba tiene una gran demanda de variedad de sabores, característico de un sector hotelero de gran calidad, pues necesita ofertar una amplia variedad de sabores de este delicioso postre en todo el sector hotelero de la región occidental del país. Esta demanda no se ha podido satisfacer y por tanto se han reducido las ventas del producto debido a la pérdida de clientes por falta de variedad de sabores. Debido a lo anteriormente expuesto es que el objetivo general del presente trabajo es definir un procedimiento de cálculo para la optimización de la distribución de sabores a producir mensualmente garantizando la minimización de los costos de calidad con la elaboración de todas las variedades de sabores que no se hacen y construir una herramienta de cálculo rápido para la realización de dicho procedimiento a nivel industrial.
Materiales y métodos
Con el objetivo de minimizar el costo de calidad por cliente perdido por falta de variedad de sabores, se decide realizar una optimización buscando el costo mínimo por consumo de materias primas con la elaboración de todas las variedades de sabores que no se producen actualmente.
Para realizar esta optimización se sigue la estrategia general de solución de problemas de optimización propuesta por Orestes Mayo y otros autores que consta de los siguientes pasos: (1,2,3,4,5,6
Análisis de la situación o problema de optimización y definición de las variables y características de interés técnico-económico.
Este paso debe estudiarse a profundidad el proceso y realizar un análisis de las alternativas posibles. Se deben definir las variables más importantes del sistema y las relaciones entre estas que son las que determinan las restricciones internas en función de los balances de masa, relaciones tecnológicas y límites físicos. También hay que examinar las restricciones externas las cuales están determinadas por aspectos que sean independientes de la situación física, como condiciones geográficas, disponibilidad, demanda y calidad de las materias primas entre otros aspectos. Además, deben definirse las características del proceso que son de interés desde el punto de vista técnico económico o en función del objetivo del problema. 1,2
La situación física o problema de optimización ha sido expuesta en la introducción del presente trabajo. Es decir, que el objetivo de la optimización es obtener el esquema óptimo de producción de sabores elaborando todas las variedades que se han dejado de producir garantizando un costo mínimo. Al conocer este esquema óptimo puede compararse con el anterior y estimar el incremento de las vetas por variedad de sabores, o lo que es lo mismo, la reducción que existía en estas por clientes perdidos por falta de variedad de sabores.
Definición del criterio de optimización y formulación de la función objetivo y las restricciones
La función objetivo del problema no es más que una función matemática que relaciona las variables de entrada y salida, incluyendo las de las restricciones. La función objetivo no es más que la traducción a términos matemáticos del planteamiento verbal del objetivo deseado en el problema. La función objetivo debe estar asociada un criterio bien definido de efectividad, pudiendo emplearse varios criterios.
Para la situación en estudio se define como criterio de optimización minimizar los costos de producción por consumo de materias primas, la cual será la variable dependiente y se estimará mediante la ecuación 1. 1,2,3,4,5,6)
Dónde: C: costo mínimo en $/mes.
Ci: costo unitario de una mezcla de helado para el sabor i en $/mezcla.
Xi: número de mezclas que se elaboran en un mes del sabor i.
Como restricciones se establecerán ecuaciones que expresen cada una de las características particulares de la situación física a considerar. 3,4,5
Determinar la solución óptima mediante la aplicación de un método de optimización adecuado
El método de optimización a aplicar depende de la naturaleza de la función objetivo y de las restricciones mediante las cuales se exprese matemáticamente la situación estudiada.
En este caso se aplica Programación lineal por ser una situación que se formula mediante una función objetivo y restricciones lineales respecto a las variables independientes. El método de solución de problemas de programación lineal es el Método Simplex, el cual se desarrolla mediante el complemento Solver de Excel, por ser una herramienta simple y de fácil acceso para los trabajadores de la fábrica, permitiendo que este algoritmo de cálculo se convierta en una herramienta de trabajo.4,5,6) Es imprescindible aclarar que las variables independientes son enteras pues la cantidad de mezclas preparadas por mes o día de producción es siempre un número entero, por lo que puede plantearse que se está realizando una programación lineal con enteros.
Chequear la validez y la racionalidad de la solución
Una vez obtenida la solución debe revisarse la racionalidad de la respuesta obtenida y si los resultados no son satisfactorios se debe revisar el planteamiento del problema junto con las variables y restricciones no consideradas anteriormente. 1,2
Resultados y discusión
Análisis de la situación o problema de optimización y definición de las variables y características de interés técnico-económico
En la industria del helado la base de cálculo empleada es una mezcla que en el caso particular de la fábrica en cuestión equivale a 300 litros. En este tipo de industria la planificación de la distribución de sabores, las fórmulas de elaboración de cada sabor, los cálculos por costos de producción, los cálculos de índices de consumo energético y de materias primar y hasta el trabajo diario del operario encargado del proceso están referidos a una mezcla. Por esto para la realización de la optimización se trabaja con número de mezclas de helados a producir por sabores y estas serán precisamente las variables independientes relacionadas en la función objetivo. 7,8,9,10 Dichas variables serán entonces variables enteras que se denominan como se lista a continuación:
X1: Cantidad de mezclas de Chocolate a producir en un mes.
X2: Cantidad de mezclas de Fresa a producir en un mes.
X3: Cantidad de mezclas de Vainilla a producir en un mes.
X4: Cantidad de mezclas de Caramelo a producir en un mes.
X5: Cantidad de mezclas de Naranja-Piña a producir en un mes.
X6: Cantidad de mezclas de Guayaba a producir en un mes.
X7: Cantidad de mezclas de Mango a producir en un mes.
X8: Cantidad de mezclas de Fresa-Bombón a producir en un mes.
X9: Cantidad de mezclas de Vainilla-Chip a producir en un mes.
X10: Cantidad de mezclas de Moscatel a producir en un mes.
X11: Cantidad de mezclas de Tiramisú a producir en un mes.
X12: Cantidad de mezclas de Yogurt a producir en un mes.
Se identificaron como características particulares a considerar que:
La capacidad productiva de la planta de helados en un mes es de 312 mezclas de helado.
La disponibilidad de materia prima en la fábrica para un mes y el consumo de ellas se muestra en la tabla 1.Dichos consumos son valores ficticios pues por secreto comercial no se divulgan las proporciones reales de los ingredientes.
No se incluyen las disponibilidades de los sabores en pastas, mermeladas y demás responsables del sabor pues son materias primas de las cuales hay disponibilidad para 5 meses de producción, según la capacidad productiva.
Plan productivo: Con el objetivo de establecer una comparación con el costo real al que se trabaja antes de la optimización se toma como referencia el número de mezclas promedio que se producen en 1 mes que es de 216 mezclas.
En la tabla 2 se muestran las demandas reales de los clientes por cada sabor de helado.
En la optimización solo se tiene en cuenta el costo de las materias primas a emplear en cada mezcla, pues se considera que el resto de los componentes del costo de producción son independientes del sabor del helado a producir.
El costo de cada mezcla se determinó por la suma de los costos de cada uno de los ingredientes que la conforman en función de la composición para cada sabor y los costos de cada ingrediente se estimaron multiplicando el costo unitario de estos por su contenido total en la mezcla. En la tabla 3 se muestran los costos de una mezcla para cada surtido.
Definición del criterio de optimización y formulación de la función objetivo y las restricciones
El criterio de optimización seleccionado como ya se planteó anteriormente es un criterio económico, en este caso, el de minimizar las pérdidas por clientes perdidos por poca variedad de sabores garantizando que los costos de producción por consumo de materias primas sean mínimos al elaborar los sabores que no se están produciendo actualmente. Este costo mínimo se representa por la letra C y se expresa en $/mes y se formula mediante la ecuación 1 obteniéndose la ecuación 2 como función objetivo.
Tomando en consideración las características particulares de la situación en estudio relacionadas en el epígrafe anterior se formulan las siguientes restricciones:
Restricción1: Capacidad productiva de la Planta de helado.
Restricción 2: Disponibilidad de Leche Entera en Polvo.
Restricción 3: Disponibilidad de azúcar.
Restricción 4: Disponibilidad de Grasa vegetal en polvo.
Restricción 5: Disponibilidad de estabilizador integrado.
Restricción 6: Disponibilidad de cocoa.
Restricción 7: Disponibilidad de cobertura de chocolate.
Restricción 8: Plan productivo.
Restricción 9: Demanda de helado de Chocolate.
Restricción 10: Demanda de helado de Fresa. 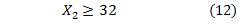
Restricción 11: Demanda de helado de Vainilla.
Restricción 12: Demanda de helado de Caramelo. 
Restricción 13: Demanda de helado de Naranja-Piña
Restricción 14: Demanda de helado de Guayaba.
Restricción 15: Demanda de helado de Mango
Restricción 16: Demanda de helado de Fresa-Bombón
Restricción 17: Demanda de helado de Vainilla-Chip
Restricción 18: Demanda de helado de Moscatel.
Restricción 19: Demanda de helado de Tiramisú.
Restricción 20: Demanda de helado de Yogurt
Restricción 21: Condición de no negatividad de las variables independientes supuesto de partida de la programación lineal.
Determinar la solución óptima mediante la aplicación de un método de optimización adecuado
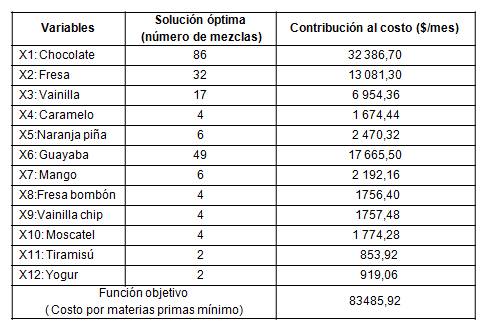
En la tabla 4 se muestran los resultados de la optimización con el complemento Solver de Excel. Como puede verse el costo mínimo mensual al que se trabajaría utilizando una mayor variedad de sabores que la actual es de 83485,92 $/mes.
También puede observarse que aunque las producciones más altas son en los sabores más económicos que también tienen alta demanda como son el chocolate y la guayaba, se respeta la demanda de fresa a pesar de tener un costo medio y se propone elaborar durante el mes el resto de la gama de sabores que garantizaría la captación de mayores ingresos a partir de que son sabores que actualmente estos clientes adquieren de la competencia.
Comparando el costo mínimo obtenido a partir de la optimización, con el costo real promedio al que trabaja la fábrica actualmente que se muestra en la tabla 5, se puede observar que aunque se encuentra por encima del costo actual lo cual es lógico pues se producen sabores que son caros y que actualmente no se están produciendo, la diferencia es de 1353,19 CUC al mes.
Esto significa un aumento del costo anual en 16 238,28 CUC. Sin embargo el estimado de pérdida de cliente por falta de variedades de sabores que se muestra en la tabla 6 fue de 28 200 CUC durante el año anterior, por lo que a pesar de aumentar el costo en la producción propuesta, se lograría recuperar estos clientes y además habría una ganancia de 4 372,56 CUC al año, que podría incrementarse con la incorporación de nuevos clientes que exigen más variedad de sabores que la que existe actualmente.
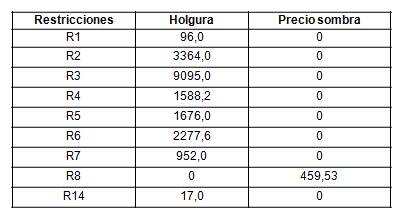
En la tabla 7 se muestran los valores de holgura y precios sombra para cada restricción. Dada la holgura que tiene la restricción de plan de producción o capacidad es posible elaborar 96 mezclas más. Esto es favorable para la planta pues significa que está en posibilidades de dar respuesta ante el incremento de la demanda.
De los resultados en las restricciones de disponibilidad se pudieran trabajar en función de llevar los inventarios a los niveles reales de producción actual, tomando en consideración la estabilidad de los productos en el mercado y la formalidad de los proveedores.
La Restricción 8 que establece el plan productivo actual, refleja un precio sombra de 459,53 CUC lo que manifiesta el costo que se incrementaría producir una mezcla más. En el escenario más desfavorable no es conveniente para la Fábrica pues se disminuiría la ganancia final aunque se ganarían los clientes.
Conclusiones
Aplicando la Programación lineal con enteros se obtuvo una distribución óptima de producción de sabores que incluye todos los sabores demandados por los consumidores y con la cual la planta trabajaría con un costo mínimo mensual de 83485,92 $/mes.
Con este esquema de producción se compensa el costo por cliente perdido pues las ganancias de la empresa aumentan anualmente en 4372,56 CUC.
El complemento Solver de Excel es una herramienta rápida y eficiente para resolver problemas de programación lineal, además accesible y de fácil comprensión para los operarios de cualquier planta de helados.