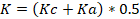INTRODUCCIÓN
El aprendizaje debe entenderse como el proceso mediante el cual el estudiante se apropia (o construye) los conocimientos, desarrolla las destrezas y habilidades, y se forma en valores y actitudes, correspondientes a los objetivos de los programas y del currículo (Martínez & Trigueros, 2020). En la concepción del proceso de enseñanza-aprendizaje los estudiantes ocupan el lugar central, al ser responsables de su propio aprendizaje por construir, por sí mismos, el conocimiento; y nadie puede reemplazarlos en esta tarea. Esto destaca el papel activo del sujeto en el aprendizaje, al enfatizar la contribución que necesariamente hace la persona que aprende en el proceso mismo de aprendizaje (Ginory & Kim, 2019).
Una preocupación de los matemáticos educativos tiene que ver con encontrar formas de intervenir y mejorar los procesos de aprendizaje de los estudiantes en las clases, para que el conocimiento matemático, cuando es aprendido por los estudiantes, se convierta en un conocimiento significativo y funcional, para que pueda integrarse a la vida para transformarlo y transformar al sujeto que aprende, lo que reconstruye y enriquece permanentemente los significados (Sauerheber & Muñoz, 2019; Rojas, 2018). Desde la perspectiva estudiantil, los universitarios encuentran muchos conceptos de «cálculo» durante su formación, en los que la integral definida es uno de los principales. No obstante, la investigación realizada hasta la fecha en este tema ha encontrado que el conocimiento de los estudiantes se limita al conocimiento procedimental, con dificultades para explicar el área negativa y conectar las diferentes representaciones de la integral definida (Fernández, Özarslan & Baleanu, 2019; Luplescu & O’Regan, 2020).
Según Bourlés (2019), la comprensión tiene lugar cuando la nueva información se conecta a través de relaciones apropiadas con el conocimiento existente. Es muy importante vincular el conocimiento conceptual y procedimental. Los estudiantes que pueden vincular los dos desarrollan un sólido conocimiento matemático; mientras que los estudiantes que son deficientes en cualquiera de los dos tipos de conocimiento, o que desarrollaron ambos como entidades separadas, no resultan completamente competentes en el manejo de conceptos matemáticos (Anaya & Cordero, 2020). De ahí que resulta necesario que se desarrollen estrategias didácticas que fomenten el aprendizaje significativo de la asignatura Cálculo Integral.
A partir de la premisa de que el paradigma tradicional centrado en el docente ha quedado obsoleto (Rico & Ponce, 2022), se debe dar paso a un nuevo modelo que pueda responder a las exigencias de la sociedad actual. El objetivo de esta investigación fue valorar una estrategia didáctica para el proceso de enseñanza-aprendizaje de la integral definida. Dicha valoración se desarrolló mediante el juicio de expertos. Los resultados de la valoración evidencian la pertinencia de la estrategia didáctica, lo cual aporta al aprendizaje de los estudiantes en la asignatura de cálculo.
DESARROLLO
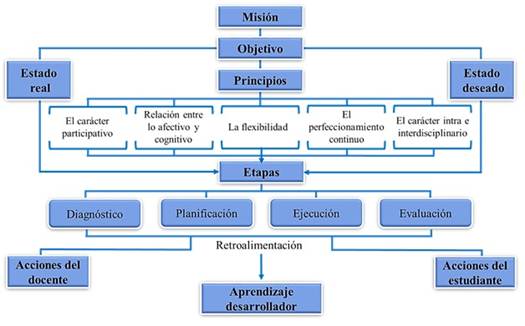
El enfoque de esta investigación fue de tipo interpretativo y presentó una orientación sobre un proceso o problema del área educacional. Además, por integrar métodos cualitativos y cuantitativos en el análisis del objeto y del campo, presentó un carácter dialéctico, el cual tuvo como fundamento «las funciones metodológicas de los niveles del conocimiento en la relación entre el ser y el pensar, en la objetividad de la verdad y el papel de la práctica como criterio valorativo del conocimiento» (Harvey, 2018, p. 270). Se recalca que el punto de partida de la investigación fue la experiencia acumulada del autor, la cual le permitió reflexionar sobre los enfoques teóricos y didácticos, integrar la información procesada y obtener como producto una estrategia didáctica para el proceso de enseñanza-aprendizaje de la integral definida. Su estructura se presenta en la Figura 1, que utilizó de forma planificada y consciente el asistente matemático Mathcad como medio de enseñanza-aprendizaje.
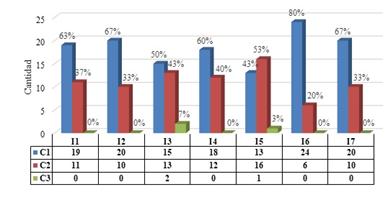
La estrategia planteada se valoró mediante un juicio de expertos y se adaptó la metodología descrita por Herrera, Calero, González, Collazo y Travieso (2022). Así, se seleccionó un total de 30 expertos competentes, de los cuales el 63 % ostentaba el título de Doctor en Ciencias Pedagógicas; y el 37 % restante, el de Máster en Ciencias de la Educación. En cuanto a la categoría docente de los expertos, 15 eran profesores titulares; 14, profesores auxiliares; y el resto, profesores instructores. Teniendo en promedio 30 años de experiencia impartiendo clases en Educación Superior. Una vez seleccionada la muestra, se denotó como Kc al coeficiente de conocimiento o información acerca del tema en investigación, determinado por el experto a partir de su valoración dentro de una escala del 0 (mínimo de conocimiento) al 10 (máximo de conocimiento), multiplicando por 0,1 (Tabla 1).
Tabla 1 Resumen del coeficiente de conocimiento de los expertos.

Fuente: Marín, Pérez, Senior y García (2021).
De los 30 expertos seleccionados para autoevaluar su coeficiente de conocimiento en el tema en estudio, resultaron 24 expertos (80 %), con un Kc alto (0,8-1,0), mientras que 6 (20 % restante) presentó un Kc medio de 0,5 a 0,7. De forma general, se obtuvo en promedio un Kc de 0,88, por lo que quedó demostrado que los 30 expertos seleccionados tenían una alta competencia en el tema de investigación.
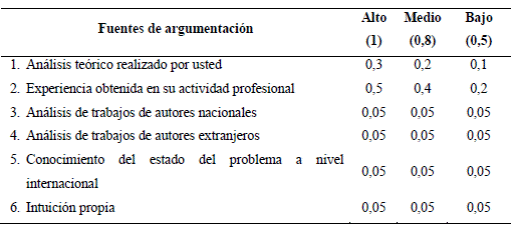
Posteriormente, se denotó por Ka el coeficiente de argumentación, estimado a partir del análisis del propio experto. En este caso se le solicitó que indicara el grado de influencia (alto, medio o bajo) de sus criterios (López, 2018), obtenido de la suma de los puntos de la valoración de cada experto en las fuentes de fundamentación definidas en la Tabla 2.
Mediante esta autoevaluación se obtuvo que 29 expertos (97 %) poseían un Ka alto de 0,8 a 1,0 y hubo un experto (3 %) con coeficiente medio (0,7), tal como se detalla en Tabla 3. En general, se tuvo en promedio un Ka de 0,94 para los 30 expertos seleccionados, lo que demostró altos conocimientos en la problemática planteada.
Una vez calculados Kc y Ka, se empleó un procedimiento basado en los criterios autovalorativos de estos, que tomó en cuenta sus competencias y las fuentes que les permitieron argumentar sus criterios. Con la finalidad de hacer objetiva la selección de los expertos, se calcularon los coeficientes de competencia K, al aplicar la siguiente expresión:
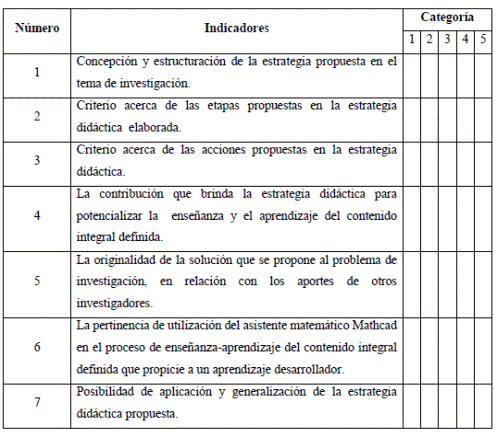
Los resultados de K reflejaron que 25 expertos (83 %) tenían un nivel de competencia alto, mientras que 5 poseían un nivel de competencia medio (17 %). En promedio el valor de K fue igual a 0,91 para los 30 expertos seleccionados, lo que indicó un nivel de competencia alto. Con posterioridad a la validación de competencia de los expertos, se aplicó una encuesta para realizar la valoración de la estrategia didáctica propuesta, que empleó valores de escala nominales (Muy adecuada, Adecuada, Poco adecuada, Inadecuada, Sin opinión), asociados de forma automática a categorías ordinales (1, 2, 3, 4 y 5, respectivamente) para facilitar la tabulación de los datos. Los indicadores de la encuesta (Tabla 4) se redactaron adaptando criterios de Zabala, García, Arciniegas, Reina, de Benito y Darder (2022) y Rojas (2018). Para el procesamiento estadístico de los datos se aplicó el modelo de Torgerson (Grace, Morton, Ward, Wilson & Kemp, 2018), mediante una hoja de cálculo en Excel.
Como resultado de la valoración de la estrategia, se obtuvo que, en mayor frecuencia, los indicadores fueron catalogados entre las categorías 1 y 2, por lo que resultaron muy adecuados o adecuados. Las valoraciones consecutivas ubicaron a los indicadores 3 y 5 en la categoría 3 (frecuencia 2 y 1, respectivamente), mientras que ningún indicador se clasificó en las categorías 4 y 5, hallazgos que se presentan en la Figura 2.
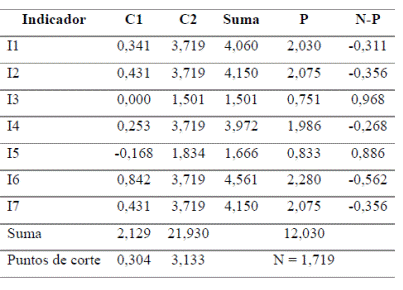
A partir de la valoración de los puntos de corte (N) y su comparación con los resultados de los parámetros de cada una de los indicadores (P), se valoró el grado de adecuación de los siete indicadores. Cada uno de los resultados obtenidos de la columna (N-P) se compararon con los puntos de corte y se determinó en qué categoría evaluativa se encontró cada indicador sometido a consulta (Tabla 5).
Con los puntos de corte y dado que la cantidad de categorías de la encuesta se redujo a dos, fue posible delimitar tres intervalos para evaluar la categoría a la que pertenecía cada indicador. De ahí se obtuvo que los indicadores I1, I2, I4, I6 e I7 resultaron menores que el primer intervalo (Figura 3), lo que permitió afirmar que los expertos consultados los consideraron muy adecuados; mientras que los indicadores I3 e I5 recayeron en la categoría de adecuado.
Delgado (2021) considera a las estrategias didácticas como el conjunto de actividades, procedimientos y recursos del docente, reflexiva y flexiblemente, para promover aprendizajes significativos en sus estudiantes y orientar de forma intencional el procesamiento de nuevos conocimientos. Se puede afirmar entonces que desarrollar el pensamiento creativo desde el aula implica la necesidad de planificar las sesiones de aprendizaje teniendo en cuenta las estrategias didácticas más adecuadas y motivadoras que despierten en el estudiante el deseo de aprender algo nuevo, y fortalezcan las capacidades creativas.
Así pues, autores como Ríos, Bernal, Gutiérrez y Gutiérrez (2020) determinaron que la aplicación de una estrategia didáctica contribuyó al «desarrollo de la construcción del contenido de integrales indefinidas y definidas desde una realidad profesional expresados en el aumento de los indicadores: estructuración metodológica, ejecución procedimental y proceder reflexivo» (p. 179). En analogía, Rodríguez, Mackenzie y Venegas (2018) destacan que la aplicación de estrategias pedagógicas en la práctica docente confirma su validez, mediante el criterio de expertos, y favorece el aprendizaje contextualizado, criterio compartido con los resultados detallados en esta investigación.
En resultados previos, la validez de las estrategias didácticas se fundamenta en los logros académicos estudiantiles, tal es el caso de Salazar, Obaya, Giammatteo y Vargas (2019), quienes determinaron una mejora significativa, relacionada con una ganancia conceptual de Hake alta (0,72), en cuanto a los conocimientos sobre los modelos atómicos. En el ámbito de la salud, Ramírez et al. (2022) validaron una estrategia mediante la prueba Chi-cuadrado al 95,0 % de confianza, que verificó la existencia de mejoras significativas en los procesos de certificación, seguimiento y atención al desempeño laboral que requieren los docentes y las unidades asistenciales del médico general. Alulema y Amancha, (2020) concluyeron que existía una correlación significativa en el uso de una estrategia didáctica aplicada a la asignatura Motores de Combustión Interna con el logro de aprendizaje estudiantil.
En lo referente al área de las matemáticas, Pérez, Valdés y Garriga (2019) encontraron que la estrategia didáctica diseñada para el contexto de la formación inicial del profesorado de matemática lograba organizar el proceso de formación y desarrollo de la habilidad profesional, a partir de tener en consideración las particularidades de la didáctica de esta asignatura. Por su parte, Ríos, Bernal, Gutiérrez y Gutiérrez (2020) detallaron cambios significativos (p < 0,05) en la apropiación de las bases conceptuales y metodológicas, así como en la construcción del contenido de Cálculo Infinitesimal desde una realidad profesional, al aplicar una estrategia didáctica en carreras de ingeniería.
Acerca de las limitaciones de esta investigación, a continuación se enlistan varias sugerencias realizadas por los 30 expertos para valorar cada uno de los indicadores propuestos en la encuesta:
Se debe abundar más en los contenidos propiamente matemáticos, puesto que se trata de un tema complejo, que, para abordarlo antes de usar los asistentes matemáticos, los estudiantes deben saber integrar correctamente.
Se puede proyectar un mayor alcance al abordar el contenido integral definida en las acciones de la estrategia, potenciado a partir del hecho de cómo las acciones de sistematización del contenido tratado sientan las bases para el estudio de las integrales múltiples, integrales de líneas, integrales de superficie, etcétera.
Es importante que se tenga cuidado con el uso del asistente matemático Mathcad en las clases prácticas y los seminarios, ya que pudiera inducir a un uso indiscriminado, incluso en aquellas cuestiones donde es innecesario o dañino.
En la aplicación de la estrategia didáctica se debe vincular el Mathcad con otras herramientas informáticas que contribuyan a enriquecer el proceso de enseñanza-aprendizaje, ya que se está trabajando con estudiantes que necesitan una utilización pertinente y acertada de estas.
Es necesario que la evaluación sea aplicada como elemento de formación de manera constante en el proceso de enseñanza-aprendizaje.
Resulta trascendental que se precise si la contribución de la estrategia didáctica es la formación integral del ingeniero agrícola o la interdisciplinariedad que se logra con las tareas propuestas.
En la evaluación de la propuesta aplicada, debe no solo diagnosticarse el avance de los estudiantes, sino valorarse cómo la estrategia didáctica contribuye en los aspectos afectivos que afectan su resultado cognitivo.
CONCLUSIONES
En correspondencia con el objetivo de la investigación y a partir del procesamiento y análisis de los resultados obtenidos, la estrategia propuesta presenta una valoración que recae en la categoría de muy adecuada, cuya fiabilidad se fundamenta en los criterios dados por los expertos, quienes, en general, presentan un coeficiente de competencia (K) alto. Desde sus opiniones, se corrobora que la estrategia didáctica planteada es factible y pertinente para contribuir al proceso de enseñanza-aprendizaje del contenido integral definida.
En tal virtud, la orientación de las investigaciones futuras sobre este campo de estudio debe centrarse en la aplicabilidad de la estrategia didáctica presentada y, por supuesto, en medir la magnitud de su impacto en el aprendizaje del contenido integral definida de los estudiantes universitarios.