INTRODUCCIÓN
Los entornos geográficos poblados y no poblados del planeta Tierra, se encuentran sistemáticamente agredidos por eventos extremos de la naturaleza. Desastres provocados por terremotos, erupción de volcanes, deslizamientos, ciclones, tsunamis, incendios, sequías e inundaciones, son cada vez más frecuentes. Tal vez este último sea uno de los más comunes registrándose un constante incremento en el número de sus ocurrencias, como consecuencia del cambio climático y del crecimiento de las áreas urbanas en zonas cercanas al cauce de los ríos.
En el estudio sobre “El valor económico de avanzar hacia un mundo hídricamente más seguro” realizado por Whittington et al. (2014), se indica que el número promedio anual de muertes provocadas por inundaciones a nivel mundial alcanza los 38577, y el promedio anual de daños sobrepasa los 11000 millones de dólares. Además de las pérdidas económicas por los daños que provocan las inundaciones, luego deben sumarse las inversiones que los países deben realizar para prevenir o mitigar los efectos de las inundaciones.
El conocimiento temprano de los efectos que puede provocar una inundación, se estudia aplicando diversas herramientas. La adquisición, transmisión y procesamiento de la información de la precipitación, de los niveles y caudales que se alcanzan en la red hidrográfica de una cuenca en particular, constituyen la base inicial sobre la cual se construyen los modelos matemáticos que permiten simular tanto el proceso hidrológico lluvia-escurrimiento, como el proceso hidráulico del tránsito de este escurrimiento a través de la red hidrográfica. Este conjunto de herramientas, previamente adaptadas a las características geográficas específicas del entorno donde se estudia la inundación, permite una predicción temprana y oportuna que debe conllevar a la toma de medidas que protejan las vidas humanas y los recursos materiales del ambiente geográfico en cuestión.
La modelación que permite reproducir el complejo sistema lluvia-escurrimiento-tránsito por la red hidrográfica, tiene numerosos factores empíricos que deben ser valorados una y otra vez hasta lograr que los modelos reproduzcan lo más fielmente posible el comportamiento de la naturaleza.
Dentro de esos factores, uno de los que más peso tiene en la modelación del comportamiento del movimiento del agua por la red hidrográfica, es la determinación consecuente del factor de resistencia dinámica del cauce y llanuras de inundación. Numerosas fórmulas empíricas, métodos para su determinación “in situ” y valores numéricos aconsejados por diversos autores e instituciones, existen como ayuda para valorar este factor. No obstante, la correcta determinación hay que hacerla en el lugar específico donde se aplica el modelo para valorar con objetividad este importante factor, que tiene una incidencia fundamental en el estudio de las inundaciones.
Al factor de resistencia dinámico que aparece en la ecuación de Manning (n) y su incidencia en el nivel que alcanzan las inundaciones se dedica este trabajo que se aplica en la cuenca del río Yanuncay que desemboca en la ciudad de Cuenca, Ecuador, provocando inundaciones en diversas zonas de la ciudad afectando la población y recursos materiales de la misma.
Para lograr el objetivo anteriormente planteado se ha simplificado el modelo de tránsito en el cauce y las llanuras, reduciéndose a un modelo hidráulico variado permanente (profundidades diferentes a lo largo de cada sección transversal sin variación temporal). Además, se empleó para cada corrida del modelo un valor de n idéntico para el cauce y las llanuras de inundación, para cuantificar el efecto de la n en la mancha de inundaciones que es el objetivo del trabajo.
ZONA DE ESTUDIO
El cantón Cuenca está ubicado al sur del Ecuador, en la provincia del Azuay, entre los 2° 39’ y 3° 00’ de latitud sur y entre los 78° 54’ y 79° 26’ de longitud oeste, a una altura aproximada de 2560 m.s.n.m. De acuerdo con el último Censo de Población y Vivienda realizado por el Instituto Ecuatoriano de Estadísticas y Censos en el año 2010, su población alcanzaba los 505585 habitantes.
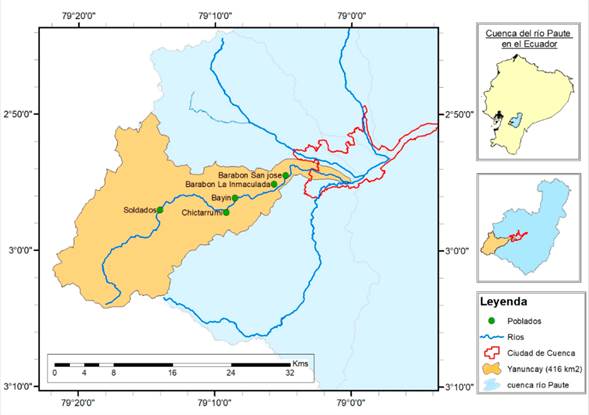
El río Yanuncay es uno de los más importantes que atraviesa la ciudad de Cuenca y se utiliza para el suministro de agua potable, el riego, la pesca y la recreación, previéndose para un futuro cercano su empleo para la generación hidroeléctrica. En su trayecto atraviesa varias comunidades y poblados como: Soldados, Bayán, Barabón y San José (figura 1). La cuenca tiene una superficie de 416 km2 hasta la confluencia con el río Tarqui; la misma forma parte de la cuenca del río Paute (6442 km2), que a su vez está dentro de la macro cuenca del río Santiago (24953,2 km2).
En la cuenca prevalece el relieve de colinas medianas y el montañoso, con pendientes en el rango comprendido entre 12 y 25 %, mientras que en la parte urbana son menores del 5 %.
El área de estudio se encuentra dentro de dos pisos climáticos: frío andino, caracterizado por lluvias torrenciales y neblina espesa y baja y templado interandino, caracterizado por vientos frecuentes en época lluviosa, y vientos fuertes con aire seco y cálido en época seca (OPS-OMS-MAE 2003). La temperatura media anual de acuerdo con las isotermas, elaboradas por el Instituto Nacional de Meteorología e Hidrología del Ecuador (INAMHI), varían entre los 2 y 16 °C.
Cuando se habla del clima es ineludible abordar el tema del cambio climático, más aún cuando la región andina tropical ha sido reconocida como un área de alta vulnerabilidad al cambio climático y los riesgos hidroclimáticos relacionados (Morán-Tejeda et al. 2016). Estudios recientes en el país muestran un incremento generalizado de la temperatura a nivel nacional, los resultados de algunos modelos indican incrementos de la temperatura media anual (a nivel nacional) de 0,6 °C para el período 2011-2040, hasta 2,8 °C para fin de siglo; en cuanto a las temperaturas máximas habría aumentos de 0,8 a 3,5 °C en los mismos escenarios. El cambio en los patrones de precipitación, las sequías prolongadas, el aumento del nivel del mar y el retroceso de glaciares, son las principales evidencias del cambio climático en el Ecuador (Cadilhac et al. 2017).
La precipitación anual fluctúa entre los 810 mm en la ciudad de Cuenca y 1400 mm en las zonas de páramo y la media anual es de 1152 mm. La lluvia en el área de estudio presenta una distribución bimodal con dos temporadas lluviosas, de enero a mayo y de octubre a diciembre, mientras que la temporada seca se observa entre junio y septiembre (Célleri et al. 2007).
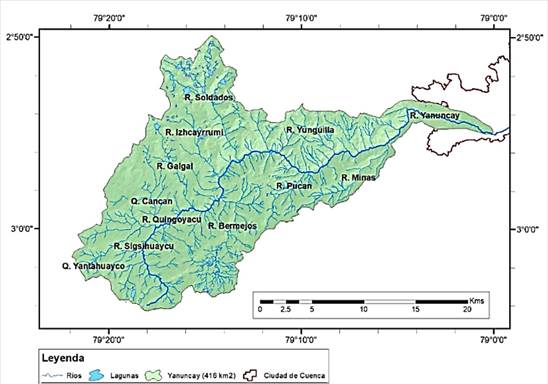
La red hidrográfica de la cuenca del río Yanuncay tiene un curso principal de alrededor de 58 km que recorre de oeste a este. Los principales afluentes, nombrados desde la parte alta de la cuenca, son: Sigsihuaycu y Yantahuayco que dan lugar al río Quingoyacu, Cancan, Galgal, Bermejos, Izhcayrrumi, Soldados, Pucán, Yunguilla y Minas. Existen algunas lagunas, sobre todo en la parte alta del río Soldados, entre las que sobresalen por su tamaño: Ventanas, Tintacocha, Amarillo Derrumbo, Patococha, Inca Casa, Cascarillas y Estrella Cocha (figura 2).
BASES DEL ESTUDIO
El estudio del movimiento del agua en un cauce natural o artificial es muy complejo ya que la profundidad depende de la ubicación geográfica de cada sección y del tiempo, ecuación (1).
donde:
x |
representa la distancia de la sección transversal estudiada desde un origen, |
t |
es el tiempo transcurrido, |
y |
representa la profundidad del flujo por el eje del cauce. |
La clasificación del régimen de circulación respecto al espacio y al tiempo en una conducción libre da tres alternativas que se diferencian en su acercamiento a la realidad y a la complejidad matemática, ellas son: régimen uniforme permanente, variado permanente y variado impermanente. Una cuarta y última clasificación, uniforme impermanente se encuentra muy rara vez en la naturaleza.
En el caso del régimen uniforme permanente, donde la profundidad de circulación no varía a lo largo del cauce, solo se presenta en cauces artificiales dada la cantidad de restricciones que deben cumplir para su existencia. La ecuación que se emplea para este régimen proviene de estudios empíricos en diversos tipos de cauces y siempre dependerá de una relación entre el caudal, la profundidad de circulación, la geometría y dimensiones del cauce, su pendiente longitudinal y un factor que considera la resistencia que el cauce le ofrece al movimiento del agua.
Una de las ecuaciones más utilizadas para este régimen de circulación fue la propuesta por Robert Manning y generalizada por Strikler años después (León y Estopiñán 1986). Esta ecuación se obtuvo a partir de la fórmula de Chezy haciendo el coeficiente C = R 1/6/n y promediando otras fórmulas empíricas de diversos autores.
donde:
Q |
es el caudal que atraviesa la conducción (m3/s). |
R |
es el denominado radio hidráulico del cauce (m) que se obtiene dividiendo el área mojada (A) entre el perímetro mojado (P). |
S |
es la pendiente longitudinal del fondo del cauce expresada en tanto por uno. |
n |
es un factor empírico dimensional para cuantificar la resistencia del cauce al movimiento del agua, cuyas unidades son s/m1/3. |
La n de Manning es uno de los parámetros más importantes para cuantificar certeramente el caudal, por lo tanto, este valor debe ser determinado adecuadamente para obtener resultados satisfactorios (León y Martínez 2013). El valor n, en numerosos casos, se vuelve subjetivo y depende de la experiencia del proyectista; en el trabajo de Burnham y Davis (1990) se exponen los resultados de un interesante estudio, en el cual se realizó una encuesta a 80 profesionales de la hidráulica, a quienes se les pidió que asignen un valor de n a 10 diferentes conducciones, los resultados obtenidos demostraron la gran variabilidad, que en el caso de mayor dispersión (desviación estándar de 0,022 y media de 0,062), los valores de n propuestos por los expertos para el mismo tramo estuvieron entre 0,01 y 0,10.
En cauces naturales existe un cauce principal, que conduce el agua de los caudales bajos y medios, y unas llanuras de inundación, por donde circulará el agua de los caudales máximos, y cada uno de estos elementos presenta distinta composición de materiales, vegetación, irregularidad, obstáculos, por lo que la resistencia al flujo y por tanto la n de Manning son diferentes. En este sentido la estimación de este parámetro en cauces naturales se torna más compleja y requiere de mayor cuidado.
En caso de inundaciones el cauce está totalmente lleno y su valor de n es el representativo de ese estado. Por su parte, las llanuras de inundación tienen otra conformación en los obstáculos que se interponen al paso del flujo y el valor de n puede cambiar con los cambios de la profundidad, que en las llanuras no siempre es significativo (Arcement and Schneider 2014). En el caso del tramo de estudio, los niveles de inundación en las llanuras son relativamente muy bajos respecto al cauce, que tiene una gran capacidad de conducción.
El caudal que circula por un cauce es un factor que afecta al coeficiente de rugosidad y por lo tanto merece un análisis particular. Cuando el flujo del agua circula por el cauce principal, a medida que aumenta el nivel, la n de Manning tiende a disminuir, sin embargo, hay que considerar la sección completa del cauce, porque si el caudal es tan grande que alcanza las llanuras de inundación y la vegetación o irregularidad en la misma es considerable, la n de Manning puede aumentar, por lo tanto, es indispensable analizar el efecto del nivel en conjunto con toda la sección compuesta del cauce.
Existen varias formas de calcular la rugosidad compuesta, en función de las características hidráulicas como el perímetro mojado, el área o el radio hidráulico y así encontrar un valor equivalente con el cual evaluar las ecuaciones correspondientes a este régimen de circulación.
Como se mencionó anteriormente en muchos cauces, aún en los artificiales, la rugosidad varía a lo largo del perímetro. A esto se le suma que, para cuantificar certeramente la resistencia dinámica del cauce y las llanuras de inundación al paso de una corriente de agua, hay que considerar el cambio del valor de n como función del régimen de circulación ya que en cada uno de los tres casos posibles (permanente uniforme, permanente variado e impermanente variado), las profundidades y velocidades en cada sección son diferentes, cambiando así la resistencia del cauce al paso de la corriente de agua.
El régimen permanente y variado, que se presenta en conducciones artificiales y naturales, se caracteriza porque en cada sección transversal hay una profundidad diferente que se mantiene a lo largo del tiempo. En este caso, el valor de n cambia como función de la profundidad, la velocidad y las características de cada una de las secciones donde se está evaluando, y para un mismo perfil de flujo (curva superficial) los valores reales de la n pueden tener grandes variaciones entre una y otra sección debido no solo al cambio de la profundidad y a la velocidad de flujo, sino también a las características del material que recubre el perímetro mojado. Esto trae como consecuencia que la determinación de la n debe realizarse espacialmente, sobre todo en cauces naturales donde la variabilidad de los materiales que componen el cauce y las llanuras cambia frecuentemente.
En el régimen impermanente y variado el cambio de la n se produce de forma similar al permanente variado, pero ahora la variable tiempo tiene un papel protagónico y el efecto del tránsito de las ondas de flujo, cada una de ellas con características propias de profundidad y velocidad repercute, a veces significativamente, en los valores de la variable n.
En el caso de grandes avenidas, donde las velocidades de circulación del agua son considerables y el flujo puede alcanzar las llanuras de inundación, la correcta estimación de la n de Manning es de suma importancia, pues como se mencionó anteriormente un error en este parámetro refleja igual error en la velocidad y caudal, lo que supone un riesgo muy grande hacia la población y bienes materiales asentados en la zona.
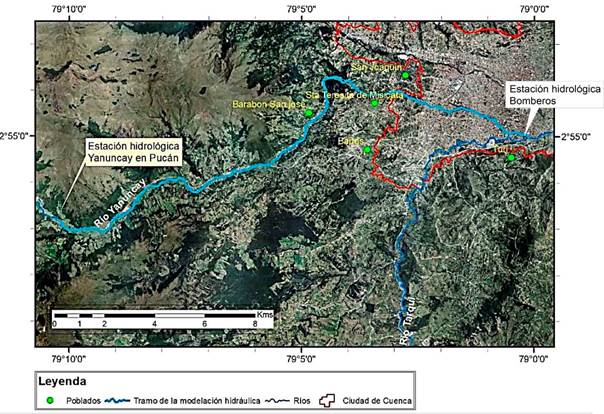
El presente estudio se realizó en el tramo del río Yanuncay, que tributa a la zona más susceptible a inundaciones, tiene una longitud de 25 kilómetros hasta su estación final aguas arriba de la confluencia con el río Tarqui justamente en la ciudad de Cuenca (figura 3).
Una estimación del valor del coeficiente de resistencia dinámico (n) del río Yanuncay fue estudiado por Fernández de Córdova et al. (2018) y sus resultados se han tomado como base para este trabajo. Del mismo se deduce que el rango de n obtenido por diferentes métodos y a partir de las formulaciones empíricas de un grupo de autores reconocidos, varía entre 0,031 y 0,073, por esta razón para este trabajo, cuyo objetivo es valorar cómo influye la correcta determinación de n en la posible mancha de inundación provocada por intensas lluvias, se adoptó un valor mínimo de n igual a 0,030 según criterios de Bruner (2016), Chow (1959), Meyer-Peter y Muller (León y Martínez 2013). Como valor máximo se empleó un valor de n igual a 0,075 apoyado en el criterio de USGS (Arcement. and Schneider 2014) y un valor intermedio de 0,055 según los resultados obtenidos por el método de los flotadores que aparecen reflejados en Fernández de Córdova et al. (2016, 2018) y los propuestos por Limerinos (León y Martínez 2013).
El resto de los valores obtenidos para la n están en el rango del mínimo-medio o medio-máximo y no es meritorio el empleo de ellos, ya que no se está evaluando el impacto de una fórmula en particular, sino el impacto específico de la variable n.
La figura 4 muestra dos vistas de la zona potencialmente inundable, se evidencia que el cauce ha comenzado a desbordarse y comienza la inundación en la llanura y en la calle que corre paralela al cauce del Yanuncay.
Para calcular el impacto de la n en la mancha de inundaciones en régimen variado y permanente se seleccionaron cuatro caudales máximos para diferentes períodos de retorno (tabla 1).
Tabla 1 Caudales utilizados con sus respectivos períodos de retorno
| Caudal (m3/s) | Probabilidad sobrepaso (%) | Período retorno (años) |
|---|---|---|
| 100 | 43,45 | 2 |
| 150 | 16,17 | 6 |
| 202 | 5,08 | 20 |
| 272 | 1,00 | 100 |
El menor de los caudales se seleccionó mayor que el caudal máximo que no desborda el cauce, de forma tal, que los cuatro caudales seleccionados tienen diferentes áreas de inundación. Por su parte, el último caudal se calculó a partir de la serie de caudales máximos anuales aplicando la distribución de probabilidades de Gumbel. Los otros dos caudales son intermedios entre estos.
El modelo hidráulico que se empleó fue el HEC-RAS desarrollado por el Cuerpo de Ingenieros de los Estados Unidos (Brunner 2016) en su versión 5.0.6. Este modelo basa el cálculo del régimen permanente variado en la ecuación de energía y permite calcular la superficie de flujo en un cauce natural o artificial de geometría simple o compuesta.
La información requerida por el modelo es la siguiente:
Las secciones que componen el tramo de estudio. Para una correcta simulación del proceso, el número de secciones debe ser el mayor posible, para esto el modelo le da la posibilidad al usuario de interpolar varias secciones, entre dos previamente medidas en el campo. Esto reduce el número de secciones que necesitan levantarse topográficamente, siempre y cuando no se pase por alto ningún cambio apreciable de la geometría.
Los caudales máximos para los que se calculan los perfiles de la superficie del agua.
Las condiciones de contorno para cada uno de estos caudales. En régimen permanente variado solo se necesita una condición que viene dada por el nivel en la sección inicial o final de tramo. Si el régimen es predominantemente subcrítico, la sección de control está aguas abajo, mientras que en el régimen supercrítico la sección de control está aguas arriba. En el único caso que el HEC-RAS necesita control aguas arriba y aguas abajo es en el denominado flujo mixto donde entre ambas secciones de control puede haber la ocurrencia de salto hidráulico (León y Estopiñán 1986).
En el caso de estudio, el criterio para los cuatro caudales analizados fue el mismo, y corresponde a una de las opciones del HEC-RAS en la cual, ingresando como dato la pendiente media del tramo final, el modelo adopta como condición de frontera la profundidad calculada mediante la ecuación de Manning.
El HEC-RAS emplea la ecuación de energía para determinar los perfiles de flujo, calculando la pérdida entre dos secciones contiguas con la distancia de separación entre las mismas y la pendiente media de la rasante de energía, para este último parámetro, el programa tiene cuatro criterios diferentes en función del régimen de flujo y tipo de perfil, si no se selecciona ninguno, asume la ecuación del promedio de la conductividad (conveyance) (Brunner 2016).
IMPACTO DEL COEFICIENTE DE RUGOSIDAD DE MANNING EN LA CUANTIFICACIÓN DE LAS INUNDACIONES
Para obtener los mapas de inundación se corrió el modelo hidráulico en el HEC-RAS en régimen variado permanente, para los cuatro caudales y los tres valores de la n de Manning, luego se exportó el archivo de resultados a un Sistema de Información Geográfica. El HEC-RAS da como resultado la mancha de agua incluido el área del cauce principal, y fue necesario restar esa zona para obtener los mapas de inundación y poder comparar los resultados (tablas 2 y 3).
Tabla 2 Área inundada para diferentes caudales y valores de n
|
|
Área inundada en km2 | |||
|---|---|---|---|---|
| Q = 100 m3/s | Q = 150 m3/s | Q = 202 m3/s | Q = 272 m3/s | |
| 0,030 | 0,081 | 0,211 | 0,384 | 0,693 |
| 0,055 | 0,122 | 0,294 | 0,513 | 0,806 |
| 0,075 | 0,208 | 0,431 | 0,668 | 0,978 |
Tabla 3 Área inundada en exceso respecto a la n = 0,030
| Caudal | Área inundada | Área inundada en exceso respecto a la |
|||
|---|---|---|---|---|---|
|
|
|
|
|||
| (m3/s) | (km2) | (km2) | % | (km2) | % |
| 100 | 0,081 | 0,041 | 51 % | 0,127 | 157 % |
| 150 | 0,211 | 0,083 | 39 % | 0,220 | 104 % |
| 202 | 0,384 | 0,129 | 34 % | 0,284 | 74 % |
| 272 | 0,693 | 0,133 | 19 % | 0,285 | 41 % |
En las figuras 5 y 6 se presentan las manchas de inundación y sus incrementos para cada uno de los caudales y valores de n analizados.
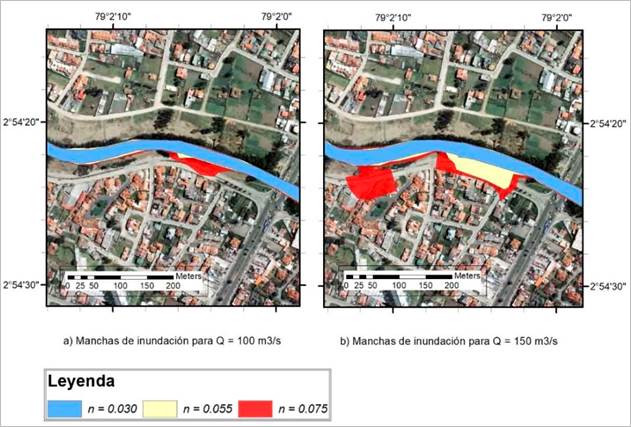
Figura 5 Manchas de inundación y sus incrementos para los diferentes valores de n: a) Q = 100m3/s, b) Q = 150m3/s

Figura 6 Manchas de inundación y sus incrementos para los diferentes valores de n: a) Q = 202m3/s, b) Q = 272m3/s
Como se aprecia en la tabla 2 el área inundada, para todos los caudales, es mayor a medida que se incrementa el valor de la n de Manning, en los dos caudales más bajos estudiados, que son los que se producen con mayor frecuencia porque tienen períodos de retorno menores (2 y 6 años respectivamente) las áreas inundadas se incrementan en más del doble si se comparan los valores obtenidos con n igual a 0,030 y 0,075. En la tabla 3 se observa que el incremento del área inundada con respecto al obtenido con el menor valor de la n = 0,030 varía entre un 51 % y 19 % para n = 0,055, y entre 157 % y 41 % para n = 0,075.
CONCLUSIONES
Se evidencia claramente el cuidado que se debe tener para definir bien el coeficiente de resistencia al flujo, ya que adoptar un valor muy bajo de n podría generar áreas de inundación que queden por debajo de las que se producirían en la realidad, más aún, esto sería de gran importancia cuando se utilice la n de Manning en la modelación hidráulica de eventos extremos para establecer zonas de desbordamiento de un río, pues la definición errónea de este valor puede generar grandes pérdidas económicas, pero sobre todo, podrían perderse vidas humanas.
El coeficiente de rugosidad de Manning debe ser determinado para cada lugar en particular, ya que son múltiples los factores que lo afectan y depende en gran medida de las características de la zona, esto a su vez asegura que los niveles de agua del río obtenidos en la modelación se acerquen mucho más a la realidad.
Para este estudio se obtuvo, de forma general, que a medida que se incrementa el caudal, para valores que desbordan el tramo en estudio, el efecto de la n de Manning sobre el valor del área de inundación es menor, pero siempre mayores para valores superiores de la n equivalente del cauce.
La tendencia matemática de la disminución porcentual de las áreas con el caudal para el tramo estudiado sigue una ecuación monótona decreciente del tipo exponencial (% de decremento de las áreas= K*e^a). Siendo más fuerte el decremento en el caso del valor de n igual a 0,075.
Es de interés, que en el tramo estudiado el crecimiento de las áreas inundadas respecto a los valores de los caudales que desbordan el cauce es marcadamente exponencial para el menor valor de n pasando a ser totalmente lineal para el mayor valor. Este resultado refuerza el primer párrafo de las conclusiones respecto al empleo de valores muy bajos del coeficiente de resistencia dinámico.