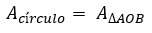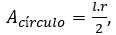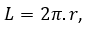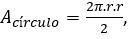Introducción
En la Conferencia Mundial sobre la Ciencia para el siglo XXI, auspiciada por la UNESCO y el Consejo Internacional para la Ciencia, se declaraba: “Para que un país esté en condiciones de atender a las necesidades fundamentales de su población, la enseñanza de las ciencias y la tecnología es un imperativo estratégico. Como parte de esa educación científica y tecnológica, los estudiantes deberían aprender a resolver problemas concretos y a atender a las necesidades de la sociedad, utilizando sus competencias y conocimientos científicos y tecnológicos”. (Open Society Institute, 2002).
La utilización de las competencias y conocimientos tecnológicos ha ocupado un lugar relevante en el sistema de enseñanza, tanto para profesores como estudiantes, pues estos se consideran como elementos mediadores en las relaciones: profesor-contenido, estudiante-contenido y profesor-alumno (Bossolasco, 2013). De especial importancia en la época actual son estos conocimientos y competencias en el aprendizaje del estudiante. En analogía con las concepciones de Liátker (1990), en relación con la actividad y sus componentes, podemos afirmar que en cualquier acto elemental del conocimiento (aprendizaje) existe una tríada: sujeto-medio-contenido, donde el medio es el núcleo de dicha tríada.
En el aprendizaje de la matemática los medios tecnológicos, tal y como señalan Álvarez, Villegas & Almeida (2014), favorecen una penetración más profunda en el contenido que se estudia mediante una actividad matemática más experimental, de búsqueda del conocimiento, de establecimiento de conexiones, pero además, contribuyen a activar y motivar a los alumnos hacia el estudio.
La introducción de los medios tecnológicos conocidos como software (en particular, los software libres, ) en el proceso de enseñanza-aprendizaje de la matemática, pueden hacer realidad una de las sugerencias didácticas ofrecidas por Puig Adam (1959)-citado por Rico & Sierra (1994), en su Decálogo de la Didáctica de la Matemática Media, referida a enseñar matemática guiando la actividad descubridora del alumno, que más tarde Freudenthal (1991)- citado por Gravemeijer & Teruel (2000), denominara reinvención guiada y que se erigiera en uno de los principios de la llamada Matemática Realista.
Estas sugerencias, encuentra en este software libre una forma de materializarse, y más aún en los momentos actuales donde existe cierto consenso en que la enseñanza no es un proceso de transmisión de conocimientos sino un proceso de creación de las posibilidades para su construcción o descubrimiento (Freire, 2010).
En este trabajo se exponen algunas ideas sobre la utilización del GeoGebra en las clases de matemática en la secundaria básica para propiciar, no solo, la búsqueda de conocimientos matemáticos, sino también para que el alumno reconozca la existencia de determinadas relaciones entre entes matemáticos que con su ayuda puede descubrir.
Desarrollo
En los lineamientos o ideas claves para el trabajo metodológico de la asignatura matemática en la escuela cubana, válidos para los diferentes subsistemas de Educación y puestos en vigor desde el curso 2004-2005, se precisa el enfoque metodológico general de esta, y por ende, los métodos y procedimientos para la dirección del proceso de enseñanza-aprendizaje, con vista al logro de sus objetivos y la consecuente elevación del interés hacia su aprendizaje (Álvarez, et al., 2014).
La novena idea clave hace alusión explícita a la utilización de las tecnologías, incluidas las de la informática y la comunicación, con el objetivo de adquirir conocimientos y racionalizar el trabajo de cálculo, pero también con fines heurísticos.
Al respecto, Álvarez, et al. (2014), plantean: ”Uno de los asistentes matemáticos desarrollados como software libre más popular en los últimos años es GeoGebra, un recurso escrito en Java y disponible en múltiples plataformas. Este permite el dinamismo de las figuras geométricas, lo que facilita analizar la variación o no de sus propiedades y relaciones al modificarlas. Asimismo, posibilita examinar un objeto matemático en diferentes registros de representación, por medio de la articulación de su interfaz gráfica con una algebraica, una de cálculo simbólico y una hoja de cálculo, lo que favorece el establecimiento de relaciones y una comprensión más profunda de lo que se estudia”.(p. 27)
Si bien es cierto que los docentes reconocen las amplias posibilidades que ofrece el uso de este software en el proceso de enseñanza-aprendizaje de la matemática, no podemos afirmar que su uso se haya generalizado y mucho menos que esto se haya convertido en una práctica habitual en el desarrollo de las clases, lo que obedece a múltiples razones, entre ellas se pueden mencionar: en primer lugar, el miedo y la insuficiente preparación de los profesores para hacer uso de esta herramienta tecnológica en sus clases, y en segundo lugar, el equipamiento tecnológico con que actualmente cuentan los centros de enseñanza, el cual resulta insuficiente y no siempre está en las mejores condiciones.
Características y ventajas del GeoGebra que permiten su utilización en el proceso de enseñanza - aprendizaje de la matemática en la secundaria básica
El programa GeoGebra fue ideado por Markus Hohenwarter en el marco de su trabajo de tesis de Maestría, presentada en el año 2002 en la Universidad de Salzburgo, Austria. Se esperaba lograr un programa que reuniera las virtudes de los programas de geometría dinámica, con las de los sistemas de cálculo simbólico. El creador de GeoGebra valoraba todos estos recursos para la enseñanza de la matemática, pero notaba que, para el común de los docentes, los programas de cálculo simbólico resultaban difíciles de aprender, dada la rigidez de su sintaxis, y que por esta razón evitaban su uso. Por otro lado, observaba que los docentes valoraban de mejor manera los programas de geometría dinámica, ya que su interfaz facilitaba su utilización. Así fue cómo surgió la idea de crear GeoGebra. Rápidamente el programa fue ganando popularidad en todo el mundo y un gran número de voluntarios se fue sumando al proyecto desarrollando nuevas funcionalidades, materiales didácticos interactivos, traduciendo tanto el software como su documentación a decenas de idiomas, colaborando con nuevos usuarios a través del foro destinado para tal fin. En la actualidad, existe una comunidad de docentes, investigadores, desarrolladores de software, estudiantes y otras personas interesadas en la temática, que se nuclean en los distintos Institutos GeoGebra locales que articulan entre sí a través del Instituto GeoGebra Internacional.
El GeoGebra es un software interactivo de matemática que reúne dinámicamente geometría, álgebra y cálculo. Hohenwarter (2014), eligió GeoGebra con el atenuante que el docente pueda tener una herramienta didáctica que ayude en el proceso de la educación, con las consideraciones que el software a utilizar sea accesible, libre, de fácil manipulación, que cuente con un proceso de instalación automático, sencillo y que sea aceptado en todas las plataformas.
GeoGebra ofrece tres perspectivas diferentes de cada objeto matemático: una vista gráfica, una vista numérica, vista algebraica y, además, una vista de hoja de cálculo. Esta multiplicidad permite apreciar los objetos matemáticos en tres representaciones diferentes: gráfica (como en el caso de puntos, gráficos de funciones), algebraica (como coordenadas de puntos, ecuaciones), y en celdas de una hoja de cálculo. Cada representación del mismo objeto se vincula dinámicamente a las demás en una adaptación automática y recíproca que asimila los cambios producidos en cualquiera de ellas, más allá de cuál fuera la que lo creara originalmente.
La versión 5 del programa ofrece las siguientes vistas que se vinculan dinámicamente:
Vista gráfica 2D: En esta vista se pueden realizar construcciones geométricas utilizando puntos, rectas, segmentos, polígonos, cónicas, etc. También se pueden realizar operaciones tales como intersección entre objetos, traslaciones, rotaciones, etc. Además, se pueden graficar funciones, curvas expresadas en forma implícita, regiones planas definidas mediante desigualdades, etc.
Vista algebraica: Allí se muestran las representaciones algebraicas y numéricas de los objetos representados en las otras vistas del programa.
Vista gráfica 3D: En esta vista se pueden representar, además de los objetos mencionados para la vista gráfica 2D, planos, esferas, conos, poliedros, funciones de dos variables.
Vista CAS (Cálculo Simbólico): Permite realizar cálculos en forma simbólica (derivadas, integrales, sistemas de ecuaciones, cálculo matricial, etc.).
Vista de Probabilidades y Estadística: Esta vista contiene representaciones de diversas funciones de distribución de probabilidad y permite calcular la probabilidad de las mismas en un determinado intervalo. También ofrece una calculadora que permite realizar test estadísticos.
El GeoGebra cuenta con un manual de ayuda elaborado por Markus Hohenwarter y Judith Hohenwarter (2009), el cual ofrece indicaciones precisas para su utilización y que se puede obtener en el sitio Web: www.geogebra.org. Varios investigadores se han referido a las bondades de este software.
González, Gutiérrez & Sandoval (2017), consideran que el GeoGebra contribuye en muchos aspectos a mejorar las metodologías de enseñanza-aprendizaje y para la solución de problemas académicos proporcionando información valiosa en aspectos gráficos, lo cual genera interés en la aplicación de esta herramienta para la resolución de problemas
García (2014), considera que el GeoGebra es un recurso tecnológico que puede ser utilizado en el aprendizaje y que debe ser incluido en la planificación de una clase como material didáctico para el desarrollo de actividades.
Bonilla (2013), indica que gracias a que GeoGebra permite obtener el resultado del ejercicio de una función de forma rápida y precisa, se le comienza a emplear después de sustentar la teoría de cada concepto (recta, exponencial), que se detallan en el contenido matemático para verificar los resultados que se obtienen al resolver los ejercicios de forma tradicional.
Márquez (1999), indica que es importante, que un conjunto de técnicas dinámicas sea incluido como una marca competitiva en la práctica de las matemáticas, pudiendo considerar a GeoGebra, ya que es un software libre y de fácil manejo que permite trabajar contenidos de geometría, algebra y análisis.
Del Pino (2013), le atribuye un lugar especial al GeoGebra dentro del espectro de herramientas existentes para el aprendizaje, por los motivos siguientes:
Es software gratuito, libre y de código abierto. No les cuesta dinero a los centros educativos y pueden modificar elementos para tener funcionalidades que no se presentan en la versión estándar.
Es multiplataforma: funciona tanto si emplean una versión de Linux propio de la Comunidad Autónoma como distintas versiones de Microsoft Windows.
Es fácil de usar. Además, existen numerosas formaciones, algunas de ellas gratuitas, impulsadas por colectivos de profesores y universidades.
Es sencillo y a la vez potente. Posee una hoja de cálculo y sus numerosas vistas permiten alternar el uso de la aritmética, representaciones algebraicas, cálculo simbólico y cálculo estadístico y probabilístico.
Los autores de este trabajo no coincidimos con la visión de Bonilla, ya que el uso de este software no se puede limitar para resolver ejercicios una vez que se haya estudiado el contenido, sino que su verdadero valor como recurso didáctico es que esta es una herramienta para producir, construir y descubrir conocimientos, dando la posibilidad, al mismo tiempo, de verificar su valor de verdad.
El GeoGebra tiene las mismas ventajas de cualquier software educativo, pero sobresalen las siguientes:
Se propician varios tipos de aprendizaje que pueden ser individuales o grupales
Fomenta la creatividad: al retar el aprendizaje, a aplicar los conocimientos y habilidades que ya posibilita la búsqueda y/o descubrimiento de nuevos conocimientos.
Facilita la construcción de conocimiento por parte del alumno.
Favorece el aprendizaje autónomo y se ajusta al tiempo de que el aprendizaje puede disponer para esa actividad.
Permite el acceso al conocimiento y a la participación de actividades.
Incluyen elementos para captar la atención del alumno.
Favorece el carácter interactivo del aprendizaje.
Permite la utilización de principios heurísticos, que con otros medios resultan casi imposible de aplicar, como es el caso de la movilidad, la inducción, la generalización, entre otros.
Utilización del GeoGebra para reconocer relaciones y dependencias, así como para su descubrimiento. Dos ejemplos ilustrativos en la enseñanza de la matemática en Secundaria Básica
Uno de los contenidos que se estudian en el 8vo grado de la secundaria básica es la relación entre la amplitud del ángulo central y de los ángulos inscritos a los que corresponde el mismo arco que al ángulo central.
Para la obtención de la proposición que establece la relación entre estos ángulos, es necesario que el profesor compruebe los conocimientos previos que tiene el alumno y que sirven de base para la obtención del nuevo conocimiento.
Conocimientos previos: conceptos de radio, cuerda, ángulo central y de ángulo inscrito, así como la relación entre la amplitud del ángulo central y el arco correspondiente.
Una vez reactivado los conocimientos previos, el paso siguiente, desde el punto de vista didáctico, es que los alumnos reconozcan que esa relación existe. Para motivar la necesidad de buscar esa relación se recomienda utilizar de forma combinada la analogía y la búsqueda de relaciones y dependencias-aspectos de la motivación matemática (Jungk, 1983, Ballester, et al., 2002). Para ello, a partir de la relación ya estudiada entre la amplitud del ángulo central y del arco correspondiente, puede preguntar a los alumnos ¿sería posible entonces, que existiera alguna relación entre el ángulo inscrito y el arco correspondiente?
Para que los alumnos reconozcan que existe realmente una relación entre ambas amplitudes, puede con ayuda del GeoGebra y utilizando el principio heurístico de movilidad, que consiste en dejar invariantes una parte de las condiciones del problema y variar las restantes.
Para ello, valiéndose de la vista gráfica del GeoGebra, le orienta a los alumnos que construyan ua circunferencia de centro O y radio r cualquiera. Para ello, pide a los alumnos que seleccionen el comandocircunferencia en la barra de herrmientas, tal y como se muestra en la figura 1. Dado que esta circunferencia, por lo general tiene un centro distinto, se le pide renombrar el centro, haciendo click derecho en el punto y seleccionando la opción renombrar.
Luego se le pide situar otro punto en la circunferencia, utilizando el comandopunto y trazar un ángulo central, definiendo sus lados con el comando segmento y posteriormente se le orienta situar otro punto en la circunferencia, distinto de los dos anteriores, utilizando el comnando punto, y acto seguido se le pide trazar las cuerdas que unen ese punto con los dos puntos anteriores, utilizando el comando segmento, con lo cual queda trazado el ángulo inscrito sobre el mismo arco que el ángulo central.
Para que el alumno pueda visualizar la relación entre ambos ángulos, se le pide utilizar el comando mover punto, como se muetra en la figura, y se le pide mover uno de los puntos que están en los lados del ángulo central, por ejemplo, el punto B.
Al mover ese punto se puede percatar que si aumenta (disminuye) la amplitud del arco correpondiente al angulo inscrito, también aumenta (disminuye) la amplitud del ángulo inscito correspondiente. Un vez reconocido que existe una relación entre las amplitudes, entonces se puede lograr que formulen sin dificultad el problema a resolver: buscar la relación que existe entre un ángulo inscrito y el arco correpondiente (Figura 1).
Para que pueda formular la relación, se le pide, utilizando el comando ángulo, que indique la amplitud del ángulo central y la del ángulo inscrito correspondiente (que es la misma del ángulo central), como se muestra en la figura 2, y que compare ambas amplitudes, se le orienta utilizar la vista algebraica para que puedan ver con mayor claridad que la amplitud del ángulo inscrito es la mitad de la amplitud del ángulo central y por consiguiente la mitad de la amplitud del arco correspondiente.

Fig. 2 Vista algebraica y gráfica para comparar las amplitudes del ángulo central y del ángulo inscrito correspondiente.
Finalmente, se le pide utilizar nuevamente el comando mover punto y mover el punto para que pueda verificar que esta relación se mantiene independientemente de la posición en en que se encuentra el punto que se mueve.
De esta forma se puede pedir que formulen la correspondiente proposición:
Todo ángulo inscrito en una circunferenia tiene la mitad de la amplitud del arco correpondiente.
Se puede proceder de forma análoga si se desea que los alumnos encuentren la relación entre el ángulo semiinscrito y el arco correspondiente, trazando la cuerda AB , utilizando el comando segmento y el comando rectas especiales, para trazar la tangente a la circunferencia por los puntos A o B.
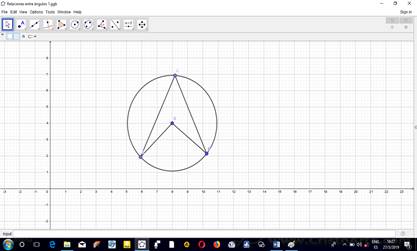
Otro de los contenidos que se estudian en el 8vo grado es el cálculo del área del círculo. Para ello se puede utilizar la primera proposición de Arquímedes, que plantea: El área de un círculo es igual a un triángulo rectángulo en el que uno de los lados que comprenden el ángulo recto es igual al radio, y el otro a la circunferencia, del círculo.
El primer paso para que los alumnos puedan encontrar la fórmula que permite calcular el área del círculo, es reactivar los conocimientos previos que posee el alumno: fórmulas para calcular el área de un triángulo rectángulo y la longitud de una circunferencia.
Para que los alumnos puedan encontrar esta proposición utilizando el Geogebra, se les pide que construyan ua circunferencia de cenro O y radio r cualquiera utilizando el comando circunferencia. De esa forma se obtiene una circunferencia y uno de sus puntos, que el alumno puede renombrar como lo desee.
Luego se les pide que indiquen la longitud y el área del círculo, utilizando el comando ángulos. Seguidamente se les orienta que definan el radio, utilizando el comando segmento, para después utilizando el comando rectas perpendiculares, trazar una tangente a la circunferencia-recta perpendicular al radio.
El paso siguiente es trazar un segmento, utilizando el comando segmento, sobre la recta perpendicular trazada, a partir del punto de tangencia, que tenga la misma longitud que la circunferencia, y finalmente, utilizar el comando polígonos, para definir el triángulo rectángulo, cuyos catetos son el segmento trazado sobre la perpendicular y que tiene la misma longitud de la circunferencia formada y el radio de la circunferencia.
Posteriormente con el comando ángulos, se indica el área del triángulo. En la vista gráfica el alumno puede comprobar que el área del círculo es igual a la del triángulo formado, tal y como se muestra en la figura 3.
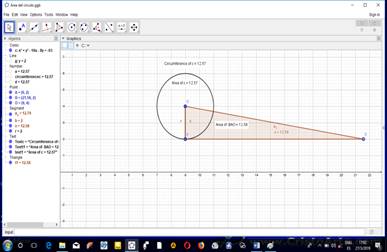
Fig. 3 Vista gráfica y algebraica para obtener la fórmula del área del círculo a partir del triángulo rectángulo de catetos 𝑟 y 𝐿.
Para comprobar que esto es cierto, puede utilizando el comando mover punto, mover el punto de contacto, de modo que disminuya (aumente) la longitud del radio y podrá verificar que el área de ambas figuras permanece invariable.
Con la ayuda del profesor, los alumnos, pueden deducir la fórmula para hallar el área del círculo planteando la igualdad:
Nótese que se está utilizando el mismo procedimiento que utilizaban los matemáticos de la antigüedad para elaborar fórmulas de áreas de figuras geométricas: comparación de áreas. Es importante que el profesor haga referencia a ello.
Como el área de un triángulo rectángulo es gual al semiproducto de sus catetos, y el ∆𝐴𝑂𝐵, tiene como cateto el radio 𝑟 y la longitud 𝑙 de la circunferencia, entonces:
pero como:
entonces:
de donde se concluye que:
Estos son solo dos ejemplos que ilustran cómo el GeoGebra, más que una herramienta para resolver ejercicios y problemas matemáticos, es un recurso didáctico que puede utilizarse para desarrollar la creatividad del alumno en las clases de Matemática, que se expresa en la búsqueda y descubrimiento de los conocimientos objeto de aprendizaje, a la vez que los familiariza con métodos propios del quehacer matemático, evidenciándose así uno de los cambios metodológicos aconsejables en la enseñanza de la matemática en el presente milenio, hacer hincapié en la adquisición de los procesos típicos del pensamiento matemático, pues como dijera De Guzmán (1993), la matemática es sobre todo saber hacer, es una ciencia donde el método predomina sobre el contenido.
Conclusiones
El GeoGebra es un elemento mediador entre el alumno y el conocimiento matemático, objeto de estudio, esta relación puede describirse mediante la tríada alumno-GeoGebra-contenido. Este no es solo un recurso didáctico para aplicar o comprobar lo aprendido, sino también, para descubrir nuevos conocimientos bajo la guía del profesor, lo cual es un objetivo alcanzable en la enseñanza de la matemática.
Los ejemplos utilizados para ilustrar cómo este software se puede utilizar en el proceso de enseñanza-aprendizaje de la matemática en la secundaria básica corroboran las ventajas de este resumidas en el trabajo y enriquecen el lineamiento o idea clave para la utilización de las tecnologías en la enseñanza de esta asignatura.