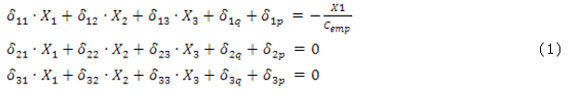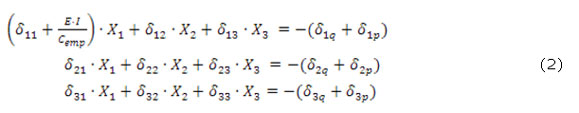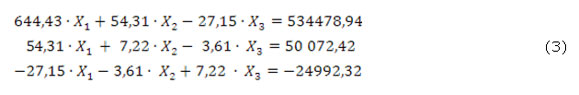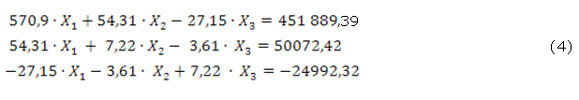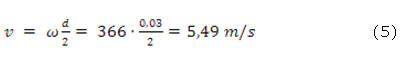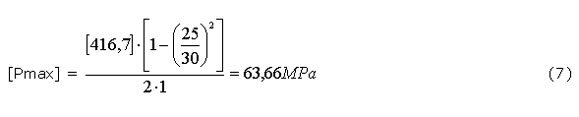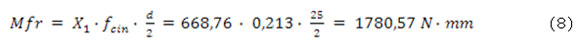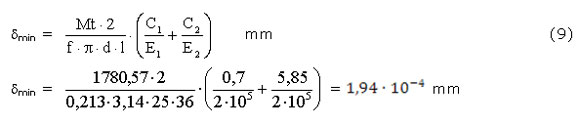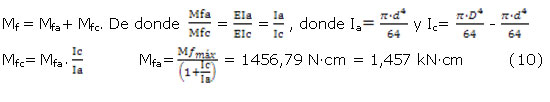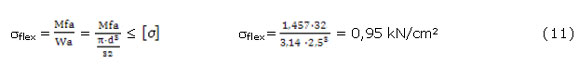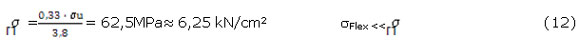ARTICULO

 

Método de cálculo para la recuperación de árboles de bombas centrífugas desgastados en la zona de las empaquetaduras

 

Calculation method for recovery of shaft of centrifugal pumps worn in the packings area

 

 

Raúl Alfonso Rodríguez^1*, Rafael Goytisolo Espinosa² y Humberto Caro González²

¹ Empresa de Cementos Cienfuegos S.A., Cuba
² Facultad de Ingeniería, Universidad de  Cienfuegos "Carlos Rafael Rodríguez", Cuatro Caminos, Cienfuegos 59430, Cuba.

*Autor para la correspondencia: Alfredo Torres, Email: [e-mail]

 

 

---

RESUMEN

Se desarrolla un método de cálculo para la recuperación de árboles de bombas centrífugas desgastadas en la zona de las empaquetaduras. El procedimiento se aplicó a la recuperación de la bomba de sulfato de alúmina utilizada en el proceso de desmineralización del agua en la Central Termoeléctrica de Cienfuegos ¨Carlos M. de Céspedes¨. El árbol se averió debido al desgaste producto de más de dos décadas de explotación. Se utiliza un novedoso Esquema de Análisis para el árbol que considera las empaquetaduras como apoyos elásticos suplementarios. Utilizando este esquema se calculó la reacción del árbol sobre la empaquetadura. Procesando los resultados de la literatura para las empaquetaduras blandas se obtuvo una ecuación de correlación entre el coeficiente de fricción cinético y el árbol, que permitió calcular el momento de fricción, hallar la presión mínima entre el casquillo y el árbol para que éste no patine. Se  halló la presión mínima del ajuste seleccionado y se verificó que ésta garantiza que el casquillo no deslice. Se evaluó la resistencia tanto del casquillo como del árbol rebajado y se verificó que ambos pueden soportar la carga.

Palabras clave: apoyos elásticos, árboles, bombas centrífugas, desgaste, empaquetaduras.

 

---

ABSTRACT

This paper develops a method for the recovery of shaft of centrifugal pumps worn area packings. The procedure was applied to the recovery pump aluminum sulfate used in the process of demineralization of water in ¨Carlos M. de Céspedes¨ Thermoelectric Plant of Cienfuegos. This equipment was damaged due to wear on the product shaft more than two decades of operation. To this end a new scheme for the Analysis of shaft packings considered as additional elastic supports is used. Using this scheme the reaction on shaft packing is calculated. Processing the results of the literature for soft packings equation correlation between the coefficient of kinetic friction and the shaft, which enabled calculation of the moment of friction, find the minimum pressure between the sleeve and the shaft so it does not slide was obtained. Dimensions and material of the sleeve is first found the maximum pressure setting selected and verified that it can be carried by the cap. Reduced resistance for the placement of sleeve and found to be burdened evaluated shaft.

Key words: elastic supports, shaft, centrifugal pumps, wear, packings.

 

---

 

 

INTRODUCCIÓN

Los soportes de los árboles de las máquinas históricamente se han idealizado a  través de tres esquemas de análisis típicos: el apoyo articulado móvil, el apoyo articulado fijo y el apoyo empotrado, sin embargo, estos esquemas idealizados se alejan en cierta medida de la realidad. Los apoyos articulados provocan en los mismos: fuerzas internas, tensiones, flechas y pendientes mucho mayores que los reales y los apoyos empotrados: fuerzas internas, tensiones, flechas y pendientes mucho menores que las que existen en la realidad. Estas insuficiencias de los esquemas de análisis se han asimilado históricamente a través del controvertido factor de seguridad, encargado de llevar sobre su espalda todas las imprecisiones e incertidumbres de los cálculos. En el presente trabajo se desarrolla una nueva metodología para el cálculo de árboles de bombas centrífugas utilizando un esquema de análisis considerando los apoyos como empotramientos parcialmente elásticos y las empaquetaduras como apoyos elásticos suplementarios. La metodología desarrollada se aplicó en la recuperación del árbol de una de las bombas de alimentación de agua desmineralizada a las Calderas de la Central Termoeléctrica de Cienfuegos que había fallado por desgaste en la zona de la empaquetadura. Si no se aplica la metodología elaborada en el presente trabajo no se hubiera podido hallar la fuerza radial que ejerce la empaquetadura sobre el árbol, no se hubiera podido hallar el par de fricción que provoca esa reacción radial sobre el árbol, tomando en cuenta el coeficiente de fricción que introduce la empaquetadura en la zona de contacto con el árbol y por lo tanto no se hubiera podido hallar la capacidad de la unión por interferencia del casquillo que se prensó en el árbol en la zona de la empaquetadura para restablecer esa zona.  El Problema Científico es que no existe un Método para evaluar el Momento de Fricción que se genera en las empaquetaduras de las bombas que permita realizar cálculos de desgaste, potencia de fricción o de recuperación de bombas desgastadas en esa zona, ya que no se puede hallar la fuerza de reacción del árbol sobre la empaquetadura. Ante esta Situación Problémica se formuló el Objetivo de que es posible, aplicando los nuevos conceptos sobre rigidez angular de los cojinetes de rodamientos (Goytisolo y col., 2006) y la novedosa consideración en la práctica de las empaquetaduras de las bombas como apoyos elásticos suplementarios (Goytisolo y col., 2010) desarrollar un procedimiento general de cálculo que permite calcular la fuerza de reacción de la empaquetadura sobre el árbol y de la posibilidad de su aplicación en la práctica en la solución de diferentes problemas vinculados con el diseño, cálculo y recuperación de los árboles de las bombas centrífugas.

 

MATERIALES Y MÉTODOS

2.1 Cálculos de la fuerza de reacción que existe en la empaquetadura

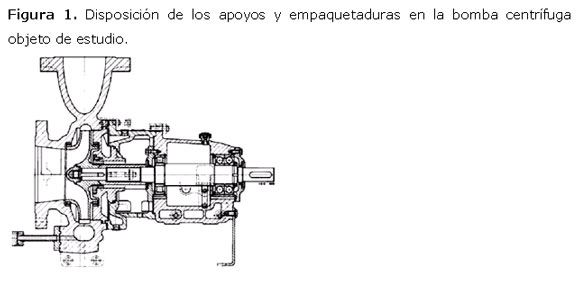
Para calcular la fuerza de reacción que existe en la empaquetadura se hace necesario utilizar un nuevo Esquema de Análisis para el cálculo de árboles de bombas centrífugas que considera precisamente las empaquetaduras de las bombas como apoyos elásticos suplementarios que es como ellas operan en la realidad y que considera además la rigidez angular de los cojinetes de rodamientos En la Figura. 1 se muestra un esquema de una bomba centrífuga radial similar a la bomba objeto de estudio. Se puede apreciar la ubicación de los cojinetes de apoyo y la ubicación de las empaquetaduras, las cuales serán consideradas como un apoyo elástico complementario.

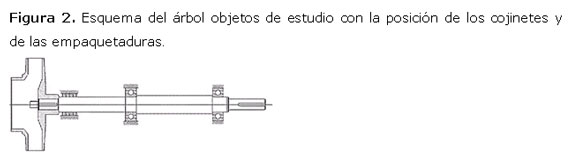
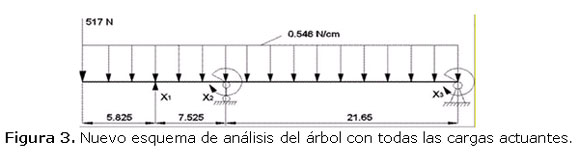
En la Figura 2 se muestra el esquema del árbol y en la Figura 3 su esquema de análisis con la carga Pi que representa el peso propio del impelente Pi = 17 N, la fuerza radial del fluido sobre el impelente Pr = 500 N, el peso propio del árbol Q = 19,11 N el cual será considerado como una carga uniformemente distribuida q = 0,546 N/cm, las empaquetaduras serán consideradas como una articulación móvil elástica, dos rodamientos de bolas radiales rígidos considerados como empotramientos parcialmente elásticos. Para resolver este sistema con apoyos elásticos en las empaquetaduras y empotramiento parcialmente elástico en las cajas de bolas radiales de simple hilera, primero hay que resolver el sistema hiperestático con los apoyos como empotramientos rígidos para hallar el momento flector que surge en cada empotramiento rígido ya que en  los  empotramientos  parcialmente  elásticos  el  momento  flector  se halla como: Mf = φ Memp, donde φ es el coeficiente de rigidez angular del empotramiento elástico. Para una caja de bolas radial rígida de simple hilera experimentalmente se demostró que   φ = 0,346 (Goytisolo y col., 2006, Goytisolo y col., 2010).

                                                    

                                                    

                                                     

Las ecuaciones canónicas del Método de las Fuerzas, Feodosiev (1985), para este caso un sistema hiperestático con tres grados de hiperestaticidad y considerando el árbol de diámetro medio contante de d = 30 mm, son:(ecuaciones 1)

 

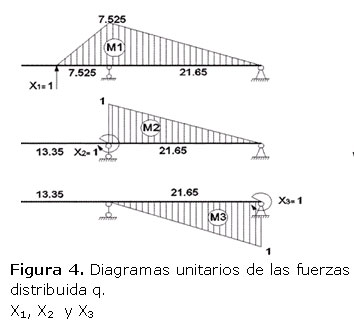
En todos los diagramas de momentos las distancias que se muestran están en cm y los momentos en N•cm. Los diagramas unitarios de las incógnitas se muestran a continuación en la Figura 4.

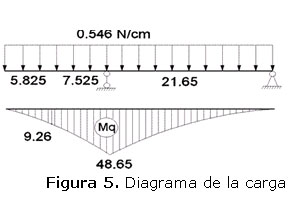
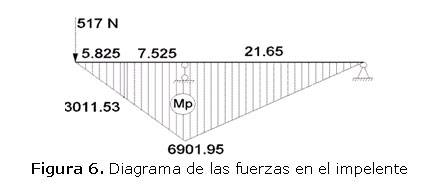
El diagrama de la carga distribuida correspondiente al peso propio del árbol se muestra en las Figura 5. El diagrama de momentos de las cargas concentradas correspondientes al peso propio de los impelentes y a la fuerza radial del fluido se muestra en la Figura. 6.

Todos estos coeficientes tanto los de las incógnitas, como los términos independientes se hallan por las Integrales de Mohr multiplicando los gráficos de las fuerzas correspondientes mediante la Regla de Vereschaguin (Pisarenko y col., 1989). Las ecuaciones canónicas después de hallar todos los coeficientes, se muestran a continuación. (ecuaciones 2)

                                                      

Sustituyendo los coeficientes en estas estas ecuaciones canónicas se obtiene:(ecuaciones 3)

 

 

En el cálculo de flechas en árboles normalmente se considera la rigidez constante con el diámetro del árbol predominante, sin embargo este árbol tiene tres tramos de diferente diámetro: d = 24 mm, en la zona del impelente, d = 30 mm en la zona de las empaquetaduras y d = 35 mm en la distancia entre apoyos. Si se consideran las diferencias de rigideces de estos tramos, las ecuaciones canónicas obtenidas son: (ecuaciones 4)

 

Como se aprecia se modifican ligeramente.

2.2. El cálculo de la unión por interferencia

Se resolvió el sistema de ecuaciones canónicas utilizando una hoja de cálculo de Excel del paquete de Microsoft Office, la cual arrojó para el caso de rigidez constante un valor de la reacción en la empaquetadura siguiente: X₁ = 668,76 N. si se calcula esta reacción considerando la rigidez real de los diferentes tramos se obtiene: X₁ = 462,84 N, sin embargo, los cálculos se realizaron con la reacción más grande, o sea, con rigidez constante, de manera de tener cierta reserva de resistencia.

Los cálculos se aplicaron en la bomba centrífuga B209 del PTQA de la Central Termoeléctrica de Cienfuegos que se utiliza para bombear alúmina en el proceso de desmineralización del agua de alimentar la caldera. Los datos de la bomba son: diámetro del árbol d = 30 mm, La presión del medio p = 0,196133 MPa, la velocidad angular del árbol ω = 366 rad/s, la temperatura del medio t = 20 °C, Empaquetadura de plástico fluorocarbúrico y grafito (ФΓ)* de dimensión 6 x 6 mm, con han = 6 anillos de la empaquetadura. La velocidad periférica del árbol en la zona de la empaquetadura es: (ecuación 5)

 

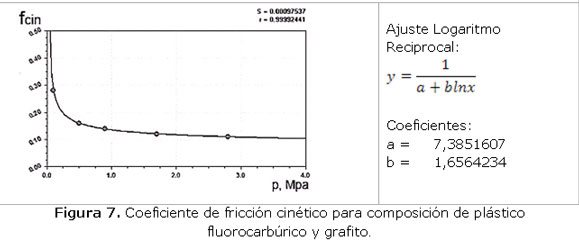
y la presión del medio p = 0,196133  MPa, de acuerdo con el ajuste realizado para esta empaquetadura utilizando el software Curve Expert (CVXPT32) a partir de los gráficos del libro  (Mijalev y col., 1984).(figura 7)

 

El coeficiente de rozamiento cinético entre la guarnición y el árbol es f_cin = 0,213.

Según la Norma Cubana NC-01-01: Selección de las desviaciones y ajustes de ISA, vigente en Cuba desde Marzo de 1972, para el ajuste prensado H7/r6 los aprietes máximos y mínimos obtenidos para el casquillo son:

25 H₇   Es = 25,021 mm                    25 r₆    es = 25,041 mm

Ei = 25,00   mm                                                              ei = 25,028 mm

A_máx = Es + ei = 0,049 mm                                          A_mín = ei – Es = 0,007 mm

El cálculo del apriete máximo que admiten el cubo y el árbol, para que no fallen durante el ensamblaje (Dobrovolski y col., 1991).

d - Apriete en la unión, mm.

d – Diámetro nominal de las piezas unidas, mm.

C₁ y C₂ – Coeficientes de Lamé.

C₁ =        y    C₂ =        

m - Coeficientes de Poisson.
d₁ – Diámetro interior de la pieza interna, mm. En el caso de un árbol macizo d₁ = 0.
d₂ – Diámetro exterior de la pieza externa, mm.

Para el apriete máximo del ajuste seleccionado, se puede calcular la presión máxima sobre el casquillo para los datos:

(ecuación 6)

                                                                  

 

La tensión admisible del acero 40 X utilizado será: [σ] = σ_f /1,2 = 500/1,2= 416,7 MPa y sustituyendo en la ecuación correspondiente para los ajustes prensados:

(ecuación 7)

 

Como p_max < [p_max]  El ajuste seleccionado es adecuado, el casquillo soporta la presión del ajuste por interferencia. La pieza interior se trata de un árbol macizo de material dúctil: p_max =  [s] / 2. En el caso analizado la presión máxima permisible por el árbol es [p_max] = 208 MPa. El árbol resiste sin problemas.

Para determinar el apriete mínimo requerido en la unión para garantizar que la unión por interferencia no deslice. En el caso objeto de estudio del presente trabajo en la unión del casquillo se genera un momento torsor igual a la reacción en la empaquetadura multiplicada por el coeficiente de fricción entre empaquetadura y árbol. La condición de no deslizamiento es el momento originado por la interferencia mínima del ajuste seleccionado sea mayor que este momento de fricción. El momento de fricción en la zona de empaquetadura es igual a la reacción X₁ por el coeficiente de fricción por el radio del árbol. El cálculo de la unión por interferencia entre casquillo y árbol se realiza para evitar el giro del casquillo por la acción del momento de fricción, de aquí que se tomará el coeficiente de fricción calculado anteriormente: f_cin = 0,213.(ecuación 8)

 

Y el apriete mínimo necesario para que no deslice el casquillo será: (ecuación 9)         

 

La interferencia mínima del ajuste es δ_min = 0,007 mm da mayor que la necesaria.

El cálculo a flexión del árbol con el diámetro reducido para la colocación del casquillo se realiza partiendo de que el momento flector en esa sección del árbol se divide una parte la asimila el casquillo y la otra la sección maciza del árbol y entre el casquillo y el árbol los momentos flectores se dividen proporcionalmente a las rigideces respectivas a flexión.

Teniendo en cuenta que el M_fmáx= 3020,79 N∙cm y s_u = 720 MPa entonces: (ecuación 10)

 

 Como: D_c = 30 mm y d = 25 mm. El diámetro real del casquillo es mayor por lo que resistirá más que el árbol por lo que se comprobará solo la resistencia del árbol.(ecuación 11)

                                                         

  (Dobrolvolski, 1991) recomienda para árboles sometidos a flexión en rotación, para evitar la fatiga en el árbol.(ecuación 12)

El árbol soporta sin que exista probabilidad de falla por fatiga en dicha sección.

 

RESULTADOS Y DISCUSIÓN

Se resolvió el sistema de ecuaciones canónicas utilizando una hoja de cálculo de Excel del paquete de Microsoft Office, la cual, para rigidez constante del árbol arrojó: 

X₁ = 668,76 N, X₂ = 1910,08 N·cm, X₃ = 8,11 N·cm

Se calcularon los valores reales del momento en los cojinetes ya que estos son parcialmente elásticos y no rígidos:

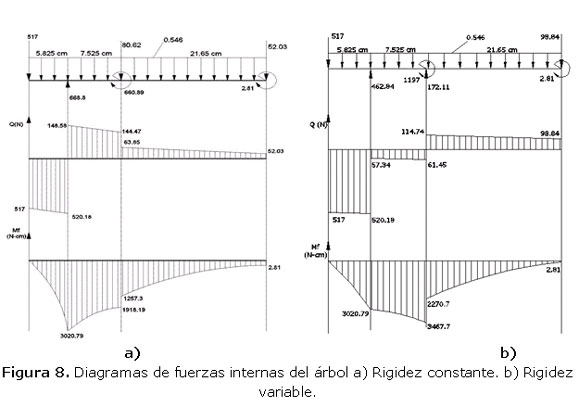
ecuación 13

 

 Con los nuevos valores reales de las incógnitas obtenidos: X_1R = 462,84 N, X_2R = 1197,03 N·cm y X_3R = 2,81 N·cm, para rigidez variable, se construyeron los diagramas de fuerzas internas para el árbol con rigidez constante  Figura 8 a) y con rigidez variable en la Figura 8 b).

 

CONCLUSIONES

1. El esquema de análisis que se utilizó para el árbol es novedoso y mucho más exacto que el clásico, en el cual se consideran las empaquetaduras como apoyos elásticos suplementarios y la rigidez angular de los cojinetes de apoyo.
2. El empleo de este esquema permitió calcular la fuerza que ejerce el árbol sobre la empaquetadura y se calculó basado en la teoría de los prensaestopas con empaquetaduras blandas el coeficiente de fricción entre empaquetadura y árbol y el par de fricción.  La interferencia mínima garantiza que el casquillo no deslice.
3. Para el casquillo se comprobó que su resistencia a la presión máxima provocada por la interferencia es adecuada, asi como la resistencia del árbol rebajado.

 

REFERENCIAS

Dobrovolski, V., Zablonski, K., Radchik, A., Erlij, L., Elementos de Máquinas., Moscú: MIR. 1991, pp. 441 – 445.

Feodosiev, V., Resistencia de Materiales., Moscú: MIR., 1985, pp. 209 - 234.

Goytisolo, R., Hidalgo, C.; Nodal, F., Noa, J.G., Estudio teórico y experimental del coeficiente de rigidez de los apoyos en árboles con diferentes cojinetes., Memorias del 3er Congreso Internacional de Ingeniería Mecánica y 1^ro de Mecatrónica., Bogotá, Colombia., 2006, 8 págs.

Goytisolo, R., Alfonso, R., Alemán, G., Monteagudo, J., Longoria, L, Morales, L., Bravo, L., Método de cálculo para árboles de bombas centrífugas considerando los cojinetes de rodamientos como empotramientos parcialmente elásticos y las empaquetaduras como apoyos elásticos suplementarios., Memorias de la VI Conferencia Científica, COMEC 2010, Villa Clara, 2010, 8 págs.

Mijalev, M.F., Tretiakov, N.P., Milchenko, A.I., Zobnin, V.V., Cálculo y Diseño de Máquinas y Aparatos de la Industria Química., Moscú Veneshtorgizdat, pp. 331-349.

Norma Cubana NC-01-01: Selección de las desviaciones y ajustes de ISA, vigente desde Marzo de 1972, 1987.

Pisarenko, G., Yakovlev, A., Matveev, V., Manual de Resistencia de Materiales., Moscú: MIR, 1989, pp. 300 – 338.

 

 

Recibido: Marzo 9, 2015;
Revisado: Abril 20, 2015;
Aceptado: Mayo 6, 2015