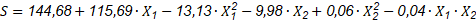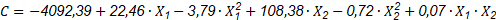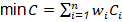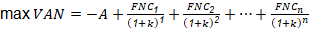INTRODUCCIÓN
El diseño de procesos de alimentos difiere del diseño de procesos químicos con respecto a los criterios y objetivos del mismo. Estas diferencias principalmente radican en la calidad que demandan los consumidores, características del producto, seguridad y costos (Hadiyanto et al., 2009). En la industria de alimentos, determinar y predecir la calidad, seguridad e impacto nutricional de la materia prima y del producto procesado se ha vuelto de primordial importancia (Rathore y Kapoor, 2016). Esta industria requiere procesos de producción flexibles para el manejo de las variaciones de los atributos del producto. La calidad es el principal criterio para el diseño de procesos de alimentos, ya que satisfacer al consumidor asegura el éxito del producto y del proceso (Hadiyanto et al., 2009).
El diseño de procesos de alimentos procura encontrar operaciones y estrategias de procesamiento para obtener productos con calidad. La optimización permite el diseño de sistemas flexibles puesto que admite encontrar las condiciones óptimas y las rutas para obtener un producto con calidad (Hadiyanto et al., 2009).
Por ello, es importante la construcción del modelo de optimización que puede utilizarse exitosamente, entre otros objetivos, para mejorar la calidad de los productos (Dobre y Sanchez, 2007). En este sentido, (Magrab et al., 2010) menciona que hay una fuerte relación entre la calidad del producto y el retorno de inversión de la compañía. Por lo tanto, la calidad del producto debe considerarse como el punto de partida para el diseño de proceso de alimentos. Entonces es esencial que los indicadores de calidad sean medibles, previsibles y se relacione con los indicadores técnicos, económicos, ambientales que integran el diseño de procesos.
Por otro lado, (Quezada et al., 2016) sugieren que los atributos de calidad organolépticos para la miel de caña son la viscosidad (V), sabor (S) y presencia de cristales (C) y un rango operacional de pH entre 3,5 a 4,5 y °Brix de 74 a 78. Sin embargo, (Cerda et al., 2017) demostraron que en ese rango operacional se obtenía un alto porcentaje de productos defectuosos, lo que según (Cerda et al., 2019) incide en el desarrollo socio-económico en la agroindustria.
Los métodos tradicionales para el diseño de procesos abordan insuficientemente la calidad desde la fase de diseño. Especialmente en las pequeñas unidades artesanales de Ecuador que procesan derivados de caña de azúcar fueron diseñadas con insuficientes criterios técnicos. El objetivo de este trabajo es proponer un procedimiento que, desde el diseño conceptual, considere la calidad del producto.
MATERIALES Y MÉTODOS
2.1 Procedimiento para el diseño de procesos considerando la calidad desde la fase de diseño
El procedimiento es una modificación al presentado por (Pérez et al., 2012) ya que este aborda insuficientemente la calidad desde la fase de diseño. Se expresan en forma esquemática los pasos a cumplir para satisfacer los objetivos del diseño de procesos de alimentos, que consta de once actividades y tres tomas de decisión.
La Fig. 1 esquematiza los pasos a seguir sistemáticamente para el diseño de procesos.
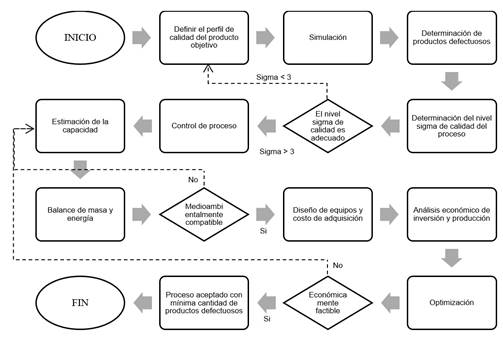
Fig. 1 Procedimiento para la determinación de las condiciones óptimas en productos alimentarios desde la fase de diseño
Los principales aspectos a desarrollar fueron:
Definir el perfil de calidad del producto objetivo: En este paso se definen los indicadores de calidad teniendo en cuenta las características organolépticas del producto alimenticio. (Quezada et al., 2016) planteó las Ecuaciones 1, 2, 3 para correlacionar los parámetros operacionales pH (X1) y °Brix (X2) con los atributos de calidad V, S, C.
Simulación: Se generan valores aleatorios de pH y °Brix con distribución de probabilidad beta. Estos parámetros influyen en los atributos de calidad (Cerda et al., 2017; Quezada et al., 2016). Se consideran tres casos para optimizar, el primero minimiza la varianza ( 2 de los atributos de calidad, el segundo maximiza el VAN, el tercero minimiza el rango operacional de pH y °Brix.
Se realizan 10 simulaciones, cada una representa la producción de un año (1560 lotes).
Determinación de productos defectuosos: Se cuantifican los productos que no satisfacen los indicadores de calidad. En el caso de la miel de caña según (Quezada et al., 2016) es aceptable para valores entre seis a 10. Se cuantifican los defectos por unidad (DPU) y los defectuosos por millón de oportunidades (DPMO)
Determinación del nivel sigma de calidad del proceso: Según (Alderete et al., 2003) un proceso aceptable tiene valores sigma mayores a 3 equivale a un 93,32% de aceptación del total de los productos.
El nivel sigma de calidad es adecuado: Es un paso de toma de decisión, donde una vez superado este nivel se garantiza que el proceso va a tener un valor igual o menor a 6,68% de productos defectuosos.
Control de proceso: En este paso se define el rango operacional de la tecnología que garantiza el perfil de calidad del producto y se propone una estrategia de control.
Estimación de la capacidad: Se estima la capacidad de la planta a partir de la demanda del mercado y la disponibilidad de materias primas.
Balance de masa y energía: El objetivo de este paso es determinar la composición de todas las corrientes que intervienen en el proceso. Los valores ceniza en el jugo de caña (0,02 %), contenido de sólidos solubles del jugo de caña que sale del filtro (18 %), metros sobre el nivel del mar (900), pérdida de calor asumida (0,9 %) y de la Tabla 1 son mediciones experimentales en la panelera “El Valle” ubicada en el cantón Puyo perteneciente a la amazonia ecuatoriana. El calor específico del vapor (2,1 kJ/kg K), coeficiente global de trasferencia de calor (285,7 W/m2 K) se tomó de (Espitia et al., 2020). Todos estos parámetros fueron incluidos en los bloques de funciones en GNU Octave.
Tabla 1 Parámetros utilizados en el balance de masa y energía
| Contenido de sólidos del jugo caña: (Filtro), (Evaporador 1), (Evaporador 2) | (18), (35), (60) | °Brix |
| Temperatura de jugo de caña que sale: (Filtro), (Calentador), | (25), (95), | °C |
| Temperatura de superficie: (Calentador), (Evaporador 1), (Evaporador 2), (Evaporador 3) | (180), (300) (260), (240) | °C |
| Tiempo de operación:(Calentador), (Evaporador 1), (Evaporador 2), (Evaporador 3) | (8681), (5588), (4834), (2562) | s |
Medioambientalmente compatible: Metodológicamente este es un paso de toma de decisión, donde una vez superado este nivel se garantiza que el proceso cumple normas medioambientales.
Diseño de equipos y costo de adquisición: En este paso se determinan los parámetros de diseño y la capacidad de los equipos. El costo de adquisición se determinará a través de un ajuste de escala y actualización de su costo según lo propuesto por (Peters et al., 2003). En este trabajo el costo de adquisición de los equipos equivale a 90 $/kg producto obtenido, según lo propuesto por la FAO (Programa de Desarrollo Agroindustrial Rural, 1992). Se utilizó ésta referencia debido que la capacidad de la planta se adapta a las condiciones de la amazonía ecuatoriana. El índice de actualización de costos para el año 1992 es de 358,2 y para el año 2019 es de 562.1 según Vatavuk, W. (2019).
Análisis económico de inversión y producción: Se tomaron los valores sugeridos por (Peters et al., 2003) para estimar los costos de inversión de una tecnología de procesamiento de sólidos y fluidos. Los valores utilizados para determinar los costos de operación corresponden a los observados en la panelera “El Valle”, número de operarios por lote 5, número de turnos por trabajador 1, número de lotes por día 10, días de trabajo al año 156, costo de operarios por hora 2 USD, costo de facilidades auxiliares 0,002 $/kg, precio de etiquetas 0,05 USD/unidad, precio envase 0,5 $/unidad, precio de la caña 0,09 $/kg, estos parámetros se utilizaron para determinar los costos variables. Para la estimación de los costos fijos se utilizaron los valores propuestos por (Peters et al., 2003). Se determinaron los indicadores dinámicos VAN, tasa interna de retorno (TIR) y margen de ganancias según la metodología de (Peters et al., 2003).
Optimización: Se determina los parámetros óptimos para el diseño del proceso. Se evalúan dos propuestas de FO: la primera es maximizar el VAN ya que según (Peters et al., 2003) la FO es casi siempre una función económica y la segunda es minimizar la ( 2 de los indicadores de calidad. En cada caso se plantea una optimización mono-objetivo. Las restricciones bajo las cuales la búsqueda se va a llevar a cabo son las relaciones adicionales en forma de balances de materia y energía y las ecuaciones de diseño.
Para la construcción del modelo, se tomó como referencia lo planteado por (Hadiyanto et al., 2009) se incluyeron los indicadores de calidad, donde el objetivo era minimizar la ( 2 de los indicadores de calidad (C) determinados en la primera etapa del procedimiento propuesto. El propósito fue encontrar el vector óptimo que minimice C. Ecuación 4:
El peso del factor (w) se asigna según la importancia de los indicadores de calidad, de tal manera que 𝑖=1 𝑛 𝑤 𝑖 =1 . En este trabajo, V, S y C se consideran de igual importancia debido que es resultado de la evaluación sensorial. Por tanto, se asigna un peso de 1/3 para cada indicador de calidad.
El pH (X1) y °Brix (X2), se consideran variables de decisión del problema de optimización. La FO que se evalúa para minimizar la ( 2 de los indicadores de calidad es (Ecuación 5):
Para maximizar el VAN se utilizó la Ecuación 6
Económicamente factible: Metodológicamente este es un paso de toma de decisión donde, una vez superado este nivel, se garantiza que la tecnología es factible desde el punto de vista económico y asegura un producto competitivo en el mercado.
Proceso aceptado con mínima cantidad de productos defectuosos: En esta etapa se tiene una propuesta de diseño óptima que ha evaluado considerando indicadores de calidad, ambientales, económicos.
RESULTADOS Y DISCUSIÓN
3.1 Definir el perfil de calidad del producto objetivo
En la primera iteración se parte con el rango operacional para pH entre 3,5 a 4,5 y °Brix de 74 a 78, y se obtiene más del 50 % de productos defectuosos. Según la escala hedónica de cero a 10 los valores aceptados son de seis a 10.
3.2 Simulación
En la Fig. 2 se observa la dispersión de los atributos de calidad. Mientras disminuye la incertidumbre del rango operacional la variable respuesta se ubica dentro del margen de aceptación, esto conlleva a controlar la variabilidad del proceso para garantizar la calidad del producto.
3.3 Determinación de productos defectuosos
Se cuantificaron los DPMO con los datos de la simulación. Se requirió al menos cuatro iteraciones para lograr menos del 6,68 % de productos defectuosos. Sin embargo, cuando se optimizan el VAN y los indicadores de calidad se tiene 0 % de productos defectuosos.
3.4 Determinación del nivel sigma de calidad del proceso
Se calculó el nivel sigma en cada iteración. En algunos lotes el nivel de aceptación del producto es total pues el nivel sigma es 6, especialmente cuando se ha optimizado el VAN y la ( 2 de los indicadores de calidad.
3.5 El nivel sigma de calidad es adecuado
En la Fig. 3 se observa que en a partir de la cuarta iteración, en la optimización del VAN y en la optimización de la calidad el proceso es aceptable ya que el nivel sigma es mayor a tres 3, esto implica a mayor nivel sigma menos productos defectuosos y un aumento en los ingresos por ventas.
3.6 Control de proceso
La incertidumbre de los parámetros operacionales conforme se realizan las iteraciones va disminuyendo. La desviación estándar ((() en la cuarta iteración del pH es 0,04 y de los °Brix es 0,15, debido a que en cada bucle se recalcula el rango operacional del pH y °Brix. Cuando se optimiza el VAN la ( del pH es 0,26 y de los °Brix es 1,05. Sin embargo, cuando se optimiza la calidad, la ( del pH y de los °Brix es cero debido que el proceso está controlado.
En esta etapa se hace necesario establecer un lazo de control que permita controlar el rango operacional del pH y de los °Brix de la tecnología propuesta.
3.7 Estimación de la capacidad
De acuerdo al ritmo de producción, se fija una producción de 1560 lotes al año en razón que las paneleras del sector trabajan 10 lotes diarios por tres días a la semana, lo que significa que el flujo de caña que entra es de 1183,75 kg/lote.
3.8 Balance de masa y energía
La composición de las corrientes que intervienen en el proceso se calcularon con el software GNU Octave. La cantidad de caña 1183,75 kg, bagazo 355,12 kg y bagacillo 57,09 kg es constante en todas las simulaciones debido que las condiciones de entrada de las materias primas se mantienen constantes en todos los estudios de caso. La cantidad de miel producida para el caso que se optimiza la calidad es 183,65 kg y cuando se optimiza el VAN es variable entre 183,47 kg a 183,56 kg.
El consumo de energía para el caso que se optimiza la calidad es 1663,47 kJ/kg de producto, este es menor que cuando se optimiza el VAN.
3.9 Medioambientalmente compatible
El vertimiento de residuos sólidos es 2,25 kg bagazo, bagacillo/kg miel para cuando se optimiza el VAN, y de 2,24 kg bagazo, bagacillo/kg miel para cuando se optimiza la calidad desde la fase de diseño. Por tanto, el procedimiento es factible desde el punto de vista ambiental en la industria de alimentos.
3.10 Diseño de equipos y costo de adquisición
Únicamente se afecta el área de transferencia de calor en el evaporador 3 debido que en esta operación se obtienen los valores de °Brix que definen la calidad y cantidad de producto. Cuando se optimiza la calidad el área es de 1,0033 m2, cuando se optimiza el VAN es variable en un intervalo de 1,0052 m2 a 1,0071 m2 en razón que hay variación en el rango operacional, mientras que cuando se busca el rango operacional óptimo, el área fluctúa entre 0,98 m2 a 0,9853 m2 en la cuarta iteración ya que el rango operacional es más pequeño y se controla especialmente que los °Brix no superen lo establecido. Esto garantiza que la carga de trabajo de los equipos diseñados no deba modificarse.
Cuando se optimiza la calidad los costos de adquisición de equipos son menores, mientras que hay variabilidad en los costos de adquisición en función de la amplitud del rango operacional.
3.11 Análisis económico de inversión y producción
En la Tabla 2, se observa que el VAN está en dependencia del rango operacional. Sin embargo, se obtiene un VAN mayor cuando se optimiza la calidad, respecto a cuando se optimiza el VAN, esto en la medida que el número de productos defectuosos es menor, debido a que aumentan los ingresos por ventas, mientras que los costos de inversión y producción no varían para cada uno de los estudios de caso. Cuando los valores de los atributos de calidad se acercan más al valor de 10 se obtienen mayores ingresos y mayor cantidad de producto.
3.12 Optimización
Se observa en la Tabla 2 el valor más alto del VAN cuando se optimizó la calidad, fue de 6629901,20 USD; mientras que cuando se optimizó el VAN, el valor fue de 6616453,31 USD.
3.13 Económicamente factible
En esta etapa según lo reportado por (Pérez et al., 2011) se toma la decisión de aceptar el rango operacional para el proceso que da valores positivos de VAN. El rango operacional óptimo se representa en la Tabla 2. No se calcularon límite superior y límite inferior para el caso de la optimización de la ( 2 ya que se tiene el valor medio y la (.
En la Tabla 2 se presentan los resultados de las 10 simulaciones de 1560 lotes. Para el caso que se utilizó la FO de minimización de la ( 2 de los indicadores de calidad en las 10 simulaciones se obtuvo el mismo VAN, el pH medio es 4,12 y °Brix medio 75,62 que fueron utilizados para el diseño. Cuando se utilizó la FO que maximiza el VAN en las 10 simulaciones se obtuvieron valores positivos diferentes, se reporta el más alto, mientras que cuando se simuló para explorar un rango óptimo fue necesario hasta cuatro iteraciones para obtener un VAN positivo que varió de 2 603 469,38 USD a 6 669 971,27 USD en dependencia del rango operacional.
Tabla 2 Búsqueda del rango operacional
| VAN (USD) | 2 603 469,38 | 6 669 971,27 | 6 629 901,20 | 6 616 453,30 |
| Costo de inversión (USD) | 126 908,52 | 127 081,68 | 126 318,08 | 126 203,77 |
| Costo de producción (USD) | 828 019,44 | 829 146,61 | 824 176,13 | 823 661,52 |
| Costo adquisición de equipos (USD) | 26 059,24 | 26 094,80 | 25 938,00 | 25 914,53 |
| pH medio | 3,79 | 3,81 | 4,12 | 4,05 |
| °Brix medio | 75,27 | 75,16 | 75,62 | 75,69 |
| pH inferior | 3,76 | 3,77 | - | 3,63 |
| pH superior | 3,83 | 3,84 | - | 4,16 |
| °Brix inferior | 75,12 | 75,02 | - | 74,61 |
| °Brix superior | 75,41 | 75,31 | - | 76,72 |
3.14 Proceso aceptado con mínima cantidad de productos defectuosos
Del análisis de la Tabla 2, y considerando que en los tres valores más alto de VAN obtenidos se obtuvo cero productos defectuosos, se selecciona el rango operacional más amplio para el diseño se procesos. Se establece entonces pH de 3,63 a 4,16 y °Brix de 75,12 a 76,73.
CONCLUSIONES
El rango operacional de pH entre 3,63 a 4,16 y °Brix entre 75,12 a 76,73 de acuerdo a las 10 simulaciones realizadas de 1560 lotes de producción garantiza que el proceso tenga un nivel sigma mayor y que los atributos de calidad estén dentro de la escala de aceptación.
El proceso con cero defectuosos reporta un VAN de 6 629 901,20 USD y margen de ganancias de 20 % que son atractivos para la inversión.
Disminuir la incertidumbre en la calidad del producto garantiza que la carga de trabajo de los equipos diseñados no deba modificarse, ya que cuando se optimiza la varianza de la calidad el área de transferencia se mantiene estable para el rango operacional seleccionado.
Si se optimiza la calidad se obtiene un VAN más altos debido a que aumentan los ingresos por ventas.