INTRODUCCIÓN
Los resultados de Cruz y col., (2020) resaltan que la matriz insumo-producto es un método de gran utilidad al momento de realizar análisis económicos de los sectores productivos de un país ya que, mediante su elaboración, se pueden obtener coeficientes económicos que brinden información para toma de decisiones eficientes.
Al reflexionar en este aspecto Boundi, (2016) resalta los propuestos por Chenery y Watanabe, (1958) y Rasmussen (1956). El primero basado en los coeficientes técnicos del modelo insumo-producto y el segundo en la matriz inversa de Leontief de dichos coeficientes. Al profundizar en este particular concluye que, el método de Rasmussen es más sólido a la hora de medir los efectos hacia atrás (BL) y hacia adelante (FL). Los reportes de Cruz y col., (2020), destacan que estos indicadores, llamados también índices de poder de dispersión (BL) e índice de sensibilidad de dispersión (FL) permiten identificar el comportamiento de las relaciones intersectoriales y clasificar a los sectores productivos como: sectores claves (BL>1 y FL>1), estratégicos o bases (BL<1 y FL>1), impulsadores o de fuerte arrastre (BL>1 y FL<1) y los sectores independientes (BL<1 y FL<1) para.
El propio autor se refiere a sector independiente, como aquellos que no provocan mayor impacto en los sectores económicos. El sector estratégico o base, presenta una demanda de insumos reducida, sin embargo, proporciona significativamente insumos a los demás sectores, que pueden constituir posibles cuellos de botella productivos Correa, (2016). El sector impulsador o fuerte arrastre impulsa el crecimiento económico de un país. El poder de dispersión o encadenamientos hacia atrás al ser mayor que la media provoca un mayor impacto sobre otros sectores, suele poseer consumo intermedio elevado y una oferta de productos que, mayoritariamente, abastece la demanda final Schuschny, (2005). Por último, el sector clave muestra altos encadenamientos productivos ya sea hacia delante como hacia atrás, tienen la capacidad de apalancar al resto ya que recogen gran parte de los flujos interindustriales de la economía Correa, (2016). Sobre este particular Pérez-Santillán, (2022) y Alarcón, (2018), aplican el procedimiento de Rasmussen para la clasificación industrial.
De acuerdo con las valoraciones de la máxima dirección del país Díaz-Canel, (2023), se necesita avanzar en la transformación integral de la empresa estatal socialista, donde, las estrategias de desarrollo territorial, desde las potencialidades endógenas de innovación, la intersectorialidad, y el conocimiento, la ciencia, la tecnología, fortalecen su proyección hacia los territorios. Para ello, es importante la manera en que se distribuyen los recursos durante los procesos de planificación de las producciones. En este sentido, y en consonancia con las valoraciones de Wilson y col., (2023), se hace necesario la realización de balances intersectoriales para garantizar la planificación de las producciones.
La empresa Sorbitol y sus derivados, ubicada en el municipio Florida, provincia de Camagüey, única de su tipo en el país con altas posibilidades de intensificar y diversificar sus producciones y un mercado seguro para la comercialización de su producto principal y otras producciones constituye actualmente una importante fuente de ingresos al territorio susceptible a procesos de mejora en cuanto a planificación e integración de su cadena de suministro.
La aplicación de la matriz insumo - producto a una industria específica en un territorio puede tener varias utilidades. Dentro de ellas cabe destacar su empleo para la evaluación de la estructura productiva de la industria y su grado de integración con otros actores económicos; la identificación de los sectores más importantes para la industria en términos de producción y consumo de insumos; y en el análisis de los efectos que generan los cambios en la demanda de los productos de la industria sobre los demás sectores de la economía. A criterio de los autores es una herramienta de análisis económico relevante referente al uso en los procesos de planificación económica - productiva.
En esta investigación se propone el empleo de la matriz insumo - producto con la finalidad de:
Perfeccionar los procesos de planificación económica de sus producciones y demás componentes de la cadena de suministro, empleando los balances de materiales y las relaciones tecnológicas que se establecen entre ellos.
Analizar el papel que desempeña la industria en el desarrollo territorial donde se encuentra enclavada.
Clasificar a la industria según el análisis insumo - producto aplicando el método de Rasmussen, para el cálculo de los índices de dispersión y de sensibilidad de dispersión para los componentes de la cadena productiva.
La matriz insumo - producto es una tabla de doble entrada simétrica que reorganiza la información obtenida en las tablas de oferta y utilización. Esta matriz muestra las relaciones económicas establecidas entre los sectores productivos y el consumo intersectorial de una economía, tomando como base las relaciones tecnológicas existentes.
La matriz muestra la cantidad de insumos que cada sector económico usa para producir un determinado producto, así como la cantidad de producción que cada sector económico realiza. Con esta información se pueden analizar las interdependencias entre los sectores económicos, las industrias y las entidades que conforman una cadena de suministro para evaluar el efecto de los cambios en la producción o el consumo de un sector sobre el resto de la economía.
Por lo que, se plantea como objetivo: aplicar los balances intersectoriales en la industria Sorbitol y sus derivados intensificada y diversificada, mediante la matriz insumo - producto para la planificación económica de sus producciones.
MATERIALES Y MÉTODOS
2.1. Matriz insumo - producto
El procedimiento seguido para la construcción de la matriz insumo - producto se describe a continuación. La tabla 1 muestra los elementos identificados para la construcción de la matriz simplificada insumo - producto para una industria objeto de interés en un territorio.
Tabla 1 Tabla insumo - producto
| Relaciones territoriales | Industria objeto de análisis | Otras relaciones | Impuestos | Producciones | |
|---|---|---|---|---|---|
| Relaciones territoriales | X11 | X12 | X13 | I1 | P1 |
| Industria objeto de análisis | X21 | X22 | X23 | I2 | P2 |
| Otras relaciones | X31 | X32 | X33 | I3 | P3 |
| Valor agregado | V1 | V2 | V3 | - | - |
| Insumo Total | X1 | X2 | X3 | - | - |
Los sectores estudiados se dividieron en tres grupos, un primer grupo que reúne a todas aquellas empresas que forman parte de la cadena productiva ubicadas dentro del territorio; la industria de interés y un tercero que reúne a todas las empresas que forman parte de la cadena de suministro que se encuentran enclavadas fuera del territorio al cual tributa la industria objeto de análisis. La misma está compuesta por los siguientes elementos:
La industria objeto de análisis, en este caso la Empresa Filial Sorbitol y sus derivados que es identificada por sus potencialidades de desarrollo, por el papel que juega dentro de la cadena de suministro que se quiere potenciar y por el rol que desempeña dentro de los aportes al desarrollo territorial.
Las relaciones territoriales establecidas entre las entidades que forman parte de las relaciones económicas y tecnológicas con la industria objeto de análisis en el territorio, en el caso objeto de estudio las entidades correspondientes a la agricultura cañera y las empresas agroindustriales Argentina y Agramonte.
Otras relaciones establecidas entre las entidades que forman parte de las relaciones económicas y tecnológicas con la industria objeto de análisis fuera de los límites del territorio. Dentro de las mismas se encuentran Suchel, Medilip y la EMI Ignacio Agramonte.
Una vez establecida la tabla, para la conformación de la matriz, se procedió a cuantificar las relaciones económicas entre cada una de ellas expresadas en valor y que representan las ventas y compras entre las entidades definidas. Las ventas, definidas en el vector fila y representadas por los valores Xij … Xin, desde j=1 hasta j=n y para las compras definidas en el vector columna y representadas por los valores Xij … Xnj, desde i=1 hasta i=n; y así sucesivamente para todos los vectores (filas y columnas), determinándose los siguientes elementos para el completamiento de la matriz:
Los valores de X ij para las filas representan las ventas (producciones) que se realizan entre las diferentes entidades para garantizar las producciones totales y para las columnas representan las demandas (materias primas, materiales y productos) que se realizan entre cada uno de ellos para garantizar las producciones.
Los Impuestos, determinados a partir de los impuestos sobre ventas realizadas y las contribuciones al desarrollo local según lo establecido por la Ley 152, (2022) de la Gaceta Oficial de la República de Cuba y calculados según Ecuación 1.
Donde: Ii (impuesto correspondiente a una fila), vij (ventas), vpi (ventas de productos que no constituyen materias primas).
Las Producciones P
i
(demandas totales), expresan en valor las cantidades de productos vendidos entre las industrias
Los Insumos (Xj), expresan en valor las cantidades de insumos demandados entre las industrias (Xij), para el desarrollo de las producciones, más el valor agregado que se genera (Vj). Constituyen los flujos de oferta total. Se determinan según la Ecuación 3.
Debido a que la matriz insumo - producto es simétrica los valores de las producciones totales (Pi) y los insumos totales (Xj) resultan coincidentes.
El Valor Agregado Bruto V j, constituye el valor creado durante el proceso productivo, se obtiene deduciendo de la producción bruta (Pi) el valor de los bienes y servicios utilizados como insumos intermedios (Xij) y se calculan según la Ecuación 4.
La Ecuación 5muestra la forma matricial de la tabla insumo - producto generado para la industria objeto de análisis, conocida también como la Matriz de Leontiev.
Un primer análisis permitió determinar los coeficientes técnicos (tabla 2), siendo estos obtenidos de la división de los elementos de la matriz de Leontiev por el valor total de las producciones correspondientes. El cálculo de los coeficientes que componen esta matriz se establece con el uso de la Ecuación 6:
Tabla 2 Coeficientes técnicos obtenidas a partir de la matriz de Leontiev
| Relaciones territoriales | Industria objeto de análisis | Otras relaciones | Demanda Final (Pronóstico) | Producciones | |
|---|---|---|---|---|---|
| Relaciones territoriales | a11 | a12 | a13 | Y1 | P1 |
| Industria objeto de análisis | a21 | a22 | a23 | Y2 | P2 |
| Otras relaciones | a31 | a32 | a33 | Y3 | P3 |
| Valor agregado | V1 | V2 | V3 | - | - |
| Insumo Total | X1 | X2 | X3 | - | - |
Una vez desarrollada la tabla, esta se puede representar en forma matricial(Ecuación 7):
Transformando la ecuación 7 y considerando que los coeficientes técnicos permanecen constantes, tomando como base el supuesto establecido por Leontiev, quien considera que la función de producción de coeficientes fijos que usa el modelo insumo - producto es lineal, entonces se determina la matriz de coeficientes técnicos de Leontiev, Ecuación 8:
Donde A es la matriz de coeficientes técnicos de Leontiev y
Podrá calcularse entonces:
Donde: X representa el insumo total; el término Inv(1-A) representa la inversa de la matriz de coeficientes técnicos de Leontiev y D la demanda proyectada.
La Ecuación (9) permitió proyectar las producciones y consumos a partir de una demanda estimada. Esto resulta de gran importancia ya que facilita los procesos de planificación económica en función de incrementos estimados de la demanda, dentro de la cadena de suministro.
Un segundo análisis posibilitó la determinación del comportamiento de la industria de interés referido a los niveles de encadenamientos productivos; estos indicadores se aplican con el fin de poder estudiar los efectos que se generan en la producción de una economía cuando se ve afectada la demanda final, además de que permiten identificar los sectores más relevantes para el funcionamiento de la economía en general.
Para este tipo de análisis de encadenamientos, se utilizarán los índices desarrollados por Rasmussen, (1956), los cuales permiten realizar comparaciones intersectoriales directas e indirectas, en base a la matriz inversa de Leontiev.
2.2. Índice de poder de dispersión
Donde: n (Número total de ramas de actividad),
2.3. Índice de sensibilidad de dispersión
Donde: n (Número total de ramas de actividad,
2.4. Clasificación sectorial
Atendiendo a los valores individuales obtenidos de cada índice y de su combinación, se ubican según su índice las relaciones en los cuatro sectores que a continuación se relacionan (tabla 3):
RESULTADOS Y DISCUSIÓN
3.1. Matriz insumo - producto para la industria Sorbitol intensificada y diversificada
Para la construcción de la matriz se partió de la construcción de la cadena de suministro para la producción de sorbitol y la consideración de las relaciones tecnológicas (índices) que se establecen en los flujos productivos y económicas o de comercialización entre las diferentes empresas que componen la cadena. En la tabla 4 se presentan las demandas de materias primas, materiales para las producciones de Sorbitol, Fructooligosacárido (FOS), Siropes saborizados y Líquido de freno. La misma, incluye, el precio por unidades de cada componente y los índices de acuerdo a las relaciones tecnológicas. Los valores se determinaron dividiendo el primero por el segundo, por tanto, significa que para obtener 1,05 t de sorbitol se requiere 1 t de glucosa, y así, sucesivamente, exceptuando el agua tratada que se relaciona con el producto, significa, por ejemplo, para producir 1 t de Sorbitol se consumen 13,7 m3 de agua tratada.
Tabla 4 Demandas por sectores económicos para nuevos escenarios productivos
| Sectores económicos | MP, materiales y productos | Cantidad | Precio ($/u) | índice |
|---|---|---|---|---|
| Industria Sorbitol (S2) | Sorbitol (t/a) | 3 016,14 | 33 814,33 | 1,05 |
| EAI Argentina (S2) | Glucosa (t/a) | 2 872,51 | 10 536,40 | 0,17 |
| EAI Agramonte (S2) | Azúcar refino (t/a) | 16 897,12 | 15 377,55 | 0,87 |
| EAI Argentina (S2) | Azúcar crudo (t/a) | 19 421,97 | 11 133,83 | 0,13 |
| Agricultura cañera (S1) | Caña de azúcar (t/a) | 149 399,80 | 800,00 | 34,55 |
| Agricultura cañera (S1) | Hectáreas de caña (ha) | 4 324,16 | - | - |
| EAI Agramonte (S2) | Agua tratada (m3) | 41 316,99 | 18,96 | 0,073 |
| Industria Sorbitol (S2) | FOS (t/a) | 1 119,28 | 2 568,65 | 1,33 |
| EAI Agramonte (S2) | Azúcar refino (t/a) | 841,56 | 15 377,55 | 0,87 |
| EAI Argentina (S2) | Azúcar crudo (t/a) | 967,31 | 11 133,83 | 0,13 |
| Agricultura cañera (S1) | Caña de azúcar (t/a) | 7 440,88 | 800,00 | 34,55 |
| Agricultura cañera (S1) | Hectáreas de caña (ha) | 215,37 | - | - |
| EAI Agramonte (S2) | Agua tratada (m3) | 3 109,11 | 18,96 | 0,36 |
| Industria Sorbitol (S2) | Sirope saborizado fructosa (L/a) | 525 000,00 | 32,45 | 1,01 |
| EAI Argentina (S2) | Sirope fructosa (L/a) | 519 487,50 | 1,82 | - |
| Industria Sorbitol (S2) | Sirope saborizado off (L/a) | 175 000,00 | 30,00 | 1,01 |
| EAI Agramonte (S2) | Sirope off (L/a) | 173 162,50 | 4,29 | - |
| Industria Sorbitol (S2) | Líquido de freno (L/a) | 1 200,00 | 37,95 | 1,59 |
| Industria Sorbitol (S2) | Sorbitol (L/a) | 753,60 | 327,02 | - |
3.2. Cálculo de la matriz insumo - producto para la industria Sorbitol intensificada y diversificada
Los resultados reflejan las relaciones técnicas económicas entre las empresas involucradas. Se cuantifica en valores las demandas, obteniéndose un total de 702 119 715,60 CUP para las relaciones territoriales, invertido en 623 476 392,10 CUP para suplir los gastos por concepto de producciones entre ellos y 43 937 786,24 CUP entregas directas a la industria sorbitol y 34 705 537,27 CUP por concepto de impuestos. En el caso, de la planta sorbitol se demandan 136 392 405,32 CUP que corresponden 9 108,00 CUP a ventas al territorio, 1 939 711,84, ventas entre la propia industria sorbitol, 127 185 704.93 CUP y de impuestos 7 257 880,56 CUP (Tabla 5).
Tabla 5 Cálculo de la Matriz insumo - Producto para la industria sorbitol intensificada y diversificada (miles de CUP)
| Relaciones territoriales | Sorbitol | Otras relaciones | Impuestos | Demanda Total | |
|---|---|---|---|---|---|
| Relaciones territoriales | 623 476, 39 | 43 937,79 | 0 | 34 705,54 | 702 119,72 |
| Sorbitol | 9,108 | 1 939,71 | 127 185,70 | 7 257,88 | 136 392,41 |
| Otras relaciones | 0 | 37 731,81 | 0 | 1 962,05 | 39 693,86 |
| Valor agregado | 78 634,22 | 52 783,10 | -87 491,84 | - | - |
| Insumo Total | 702 119,72 | 136 392,41 | 39 693,86 | - | - |
Se muestran los resultados para un incremento en la planificación de las producciones de sorbitol del 5 %. Se determinan también el porcentaje de aporte realizado por las industrias a la satisfacción de la demanda, cuyo valor mayor corresponde con un 79,01 % a las empresas del territorio (Tabla 6).
Tabla 6 Cálculo de la matriz insumo - producto para la industria sorbitol intensificada y diversificada, Proyección - Demanda 5% (miles de CUP)
| Relaciones territoriales | Sorbitol | Otras relaciones | Pronóstico de demanda | Demanda Total | % aporta indust. | Produc. a distribuir | |
|---|---|---|---|---|---|---|---|
| Relaciones territoriales | 74 340,02 | 5 238,91 | 0 | 36 440,81 | 379 128,72 | 79,01 | 20,99 |
| Sorbitol | 5,668 | 1 207,19 | 79 154,80 | 7 620,77 | 96 275,41 | 16,52 | 83,48 |
| Otras relaciones | 0 | 89 396,84 | 0 | 2 060,16 | 93 576,71 | 4,47 | 95,53 |
| Valor agregado | 304 783,03 | 432,47 | 14 421,91 | - | - | - | - |
| Insumo Total | 379 128,72 | 96 275,41 | 93 576,71 | - | - | - | - |
Los balances intersectoriales para la determinación de las demandas de los nuevos escenarios productivos, basados en las relaciones tecnológicas, muestran la integración de las producciones para el proceso de planificación de las producciones anuales y la interrelación con empresas de otros sectores económicos en el territorio. Hay que destacar que la aplicación del enfoque de Economía Circular, considera el aprovechamiento del residuo generado en la refinación del azúcar (sirope off) y el coproducto (fructosa) generado en la inversión de la sacarosa para la obtención de la glucosa, como producto deseado para ser empleado en la producción de sorbitol.
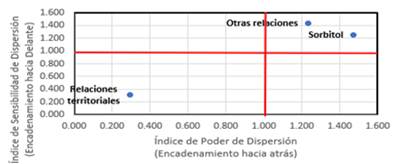
Por su parte, la determinación de los encadenamientos productivos mediante el método de Rasmussen, clasifican a la industria sorbitol y las que se relacionan con esta fuera del territorio en sectores claves, al mostrar altos valores ya sea hacia delante como hacia atrás. Igualmente se define las industrias que se relacionan dentro del territorio como sectores independientes (figura 1).
CONCLUSIONES
La aplicación de la matriz insumo - producto en la cadena de suministro con enfoque al desarrollo territorial, sustentada en las relaciones tecnológicas y económicas que se establecen, perfecciona los procesos de planificación económica de sus producciones y demás componentes de la cadena de suministro.
La determinación de los índices de Rasmussen, clasifican a la industria de sorbitol y las que se relacionan con esta fuera del territorio, en sectores claves, así como sectores independientes, a las relaciones territoriales.
Los balances intersectoriales evidencian las potencialidades que tiene la industria azucarera y sus derivados en el desarrollo del territorio, donde la empresa sorbitol es un sector clave para estos propósitos.