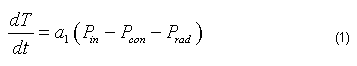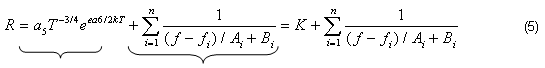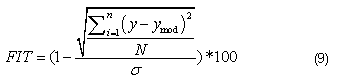TRABAJO TEORICOEXPERIMENTAL

 

Modelo dinámico para lámparas de descarga de alta intensidad en alta frecuencia

 

Dynamic model for high intensity discharge lamps in high frequency

 

Ing. Leonardo Cedeño Rodríguez^I, Dra. Susset Guerra Jiménez^II, Dr. Alexander Fernández Correa^III

  ^I Empresa de Tecnología Médica Digital, La Habana, Cuba.
 ^II Facultad de Ingeniería Eléctrica, Cujae, La Habana, Cuba.
^III Facultad de Ingeniería Eléctrica, Centro de Investigaciones y Pruebas Electroenergéticas CIPEL, Cujae, La Habana, Cuba.

 

 

---

RESUMEN

En este trabajo se desarrolla el modelado dinámico de lámparas de descarga de alta intensidad (HID en inglés), de manera que pueda contribuir al desarrollo posterior de un sistema de control avanzado sobre la etapa de potencia de un balasto electrónico, que permita operar este tipo de lámparas en alta frecuencia. El modelo tiene en cuenta la presencia del fenómeno de la resonancia acústica (RA), que usualmente se presenta en las lámparas HID a frecuencias elevadas. Para el modelado se emplean técnicas híbridas, teniendo como punto de partida las ecuaciones de balance de energía en el interior de la lámpara, en tanto para la parametrización, se aplica identificación de sistemas y optimización mediante algoritmos genéticos. La implementación del modelo se realiza con el software Matlab R2011a. Como resultado se obtiene un modelo dinámico para lámparas HID en alta frecuencia, validado para lámparas de alta presión de sodio.

Palabras clave: algoritmos genéticos, alta frecuencia, lámparas HID, modelado híbrido, resonancia acústica.

---

ABSTRACT

In this paper the dynamic modeling of high intensity discharge lamps (HID) is developed. This will contribute to the further development of an advanced control system on the power stage of an electronic ballast, which allows these lamps operate at high frequency. The model must take into account the presence of the acoustic resonance's phenomenon (AR), which usually occurs when HID lamps operates at high frequency. Hybrid modeling techniques were employed, the balance equations and the empirical expressions were obtained and the model was parameterized by identification techniques and optimization based on genetic algorithms. The implementation of the model has performed using Simulink tool of Matlab R2011a software. As a result, a dynamic model for HID lamps in high frequency has achieved and validated for high-pressure sodium lamps (HPS).

Key words: genetic algorithms, high frequency, HID lamps, hybrid modeling, acoustic resonance.

---

 

 

INTRODUCCIÓN

En nuestro país, así como en el resto del mundo, el uso racional de la energía, se ha convertido en una prioridad. Los sistemas de iluminación consumen la cuarta parte de la energía mundial, por lo cual constituye una tarea importante, la búsqueda de sistemas de iluminación más eficientes [1]. Las lámparas de descarga de alta intensidad (HID), son una fuente de iluminación atractiva, por su tamaño compacto, alta eficacia luminosa y buena calidad del color. Sin embargo su uso se ha visto limitado a la operación en baja frecuencia, pues en alta frecuencia (donde son más eficientes) se ven afectadas por el fenómeno de resonancia acústica (RA), que puede, incluso, llegar a destruir la lámpara [2]. Los diseñadores de balastos electrónicos para la operación estable de las lámparas HID, prefieren mover sus diseños a las zonas de bajas frecuencias, para evitar este fenómeno, sacrificando el rendimiento de las lámparas [3].

Algunos modelos han sido desarrollados para emular la operación en alta frecuencia de las lámparas HID, las cuales se caracterizan por un comportamiento dinámico complejo y altamente no lineal, pero los mismos solo han sido validados en lámparas HID de mercurio [4]. El objetivo del presente trabajo es extender la validez del modelo desarrollado por Jan (2005) a lámparas de sodio de alta presión (HPS, en inglés) [4], e incorporar la influencia de la RA, lo cual permitirá emplearlos en el desarrollo de sistemas de control para mejorar el rendimiento de los balastos de alta frecuencia.

LÁMPARAS HID

Las lámparas HID basan su funcionamiento en la emisión de luz que produce la descarga que ocurre en los gases que componen la lámpara al aplicársele una corriente eléctrica [5]. Los balastos son dispositivos que se encargan de la alimentación de las lámparas, haciéndolas trabajar en un régimen estable [6]. Diversos fenómenos físicos de naturaleza térmica ocurren durante el funcionamiento de las lámparas HID, que determinan sus características eléctricas [5]. Durante la vida útil de las lámparas, varios factores tanto externos como del propio funcionamiento condicionan cambios en sus parámetros que obliga al balasto a realizar cambios en la energía que entrega a las lámparas a medida que estas van envejeciendo [6].

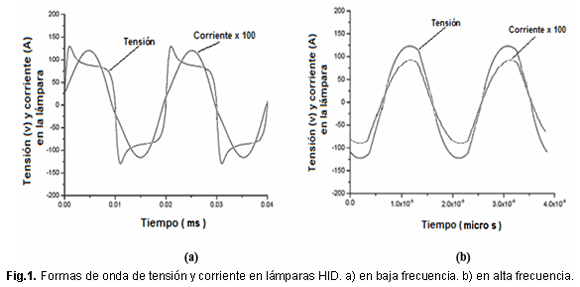
La operación en baja frecuencia figura 1a, provoca en la forma de onda de tensión de la lámpara, picos de re-ignición durante cada semi-ciclo de línea a causa del cruce por cero de la corriente y a fenómenos térmicos que ocurren durante este proceso. Esta característica de la operación en baja frecuencia reduce la vida útil de las lámparas por las sobretensiones a que se encuentran expuestas [5]. En alta frecuencia, ambas formas de onda de tensión y corriente, son sinusoidales. Como puede verse en la figura 1b, desaparecen los picos de re-ignición por la rapidez con que cruza por cero la corriente en cada semi-ciclo. El inconveniente que han encontrado los diseñadores de balastos para la operación de las lámparas HID en alta frecuencia es el fenómeno de la RA, que usualmente aparece cuando se opera las lámparas HID a estas frecuencias elevadas.

La resonancia acústica es una inclinación del arco eléctrico de la lámpara producida por las ondas de los gases del interior de la misma [2, 5]. Si la desviación del arco es significativa, pudiera llegar a la pared del tubo de descarga, dañando definitivamente la lámpara [2]. Si bien existen varias técnicas para evitar la resonancia acústica en las lámparas HID, la más interesante resulta la medición de las formas de onda de tensión y corriente de la lámpara para luego analizar el comportamiento de la resistencia de la misma, para una vez detectada la tendencia del sistema a moverse a una zona de resonancia acústica, cambiar la frecuencia de alimentación en la etapa inversora del balasto, tratando de mantener la potencia de la lámpara constante [1].

MODELADO DE LÁMPARAS HID

Actualmente existen una gran variedad de modelos para lámparas HID. Algunos de ellos se basan en considerar a la lámpara como una resistencia dinámica con retardos, los cuales están asociados a las constantes térmicas de la lámpara y representados en el modelo mediante redes RC [7]. Otros modelos se basan en la conductancia de la lámpara teniendo en cuenta las características V-I de estas [8], asociando la conductancia a la densidad de electrones libres en el interior del tubo de descarga [3], o con la presión, temperatura del arco, energía de ionización del gas de llenado y constantes que dependen por ejemplo de la geometría del tubo de descarga [3].

Las lámparas HID pueden ser modeladas mediante la implementación de técnicas híbridas, basadas en el conocimiento a priori que se tiene acerca de los procesos físicos que en ella ocurren. El modelo puede extenderse a zonas desconocidas y de gran incertidumbre de la lámpara debido a algunas suposiciones que se hagan acerca de su funcionamiento. Partiendo de las ecuaciones de balance en la lámpara se puede llegar a un entendimiento de los procesos físicos que gobiernan las propiedades de la misma. Sin embargo algunos parámetros derivados directa o indirectamente de estas ecuaciones, puede resultar de difícil obtención debido a que los fabricantes no liberan los juegos de datos de los cuales se auxilian para mejorar sus productos o porque son difíciles de obtener mediante experimentos [9].

En este tipo de procesos la técnica de optimización basada en algoritmos genéticos ha sido aplicada con buenos resultados para algunos tipos de lámparas HID de mercurio, lo que hace suponer a los especialistas que puede aplicarse al resto de las lámparas HID [4]. Basados en la metodología de modelado híbrido, propuesta por Fernández Rodríguez (2011) se procede a transitar por cada una de las etapas de la confección del modelo [10].

Conceptualización del modelo

Del estudio de las lámparas HID se conoce que sus propiedades y rendimiento están muy relacionados con fenómenos foto-térmicos. La ecuación fundamental de estos procesos es el balance de energía en la lámpara. Sus términos constituyen a su vez un grupo de expresiones no lineales, que caracterizan a las lámparas de manera general y particular.

Con el aumento de la frecuencia de operación de la lámpara, la resistencia del arco de descarga debería presentar un comportamiento resistivo puro, lo cual no ocurre en la práctica. La causa es que en la tensión de la lámpara es necesario, no solo, tener en cuenta la caída en la columna positiva del arco de descarga, sino también que existe una caída a través de ambos electrodos [5, 11], la cual suele desecharse con frecuencia para simplificar la implementación del modelo. Si se desea un modelo que emule lo suficiente la dinámica del sistema real, este término ha de ser considerado.

El modelo debe tener en cuenta la resonancia acústica, la cual se ha demostrado en el estudio de las lámparas que tiene un efecto inmediato sobre la resistencia del arco de descarga [12], por lo que el término que modela dicha resistencia tendrá que contener el efecto de las principales auto-frecuencias de la lámpara HID. La forma de detectar la RA en la lámpara será mediante la observación de su resistencia, por lo que la tensión de arco y la corriente de la lámpara son las variables de salida fundamentales del modelo a obtener. La variable manipulada del modelo será la frecuencia de la alimentación que entrega el balasto a la lámpara, pues variando esta se corrige el fenómeno de RA.

Formalización del modelo

La ecuación de balance de energía ecuación (1), establece que de la energía entregada por la fuente de alimentación a la lámpara, una parte es disipada en los electrodos y la otra en la columna de descarga. Dentro de la columna de descarga el calor es disipado por conducción térmica, convección, radiación y difusión, pero usualmente las pérdidas por convección y difusión son despreciadas cuando la lámpara es operada de forma vertical.

Donde: a₁ es un parámetro que permite realizar un mejor ajuste del modelo

P_in es la potencia consumida por la lámpara ecuación (2)
P_con son las pérdidas por conducción ecuación (3)
P_rad son las pérdidas por radiación ecuación (4)
T es la temperatura del gas de la lámpara

Donde: i es la corriente de la lámpara
R es la resistencia del arco de la lámpara

Donde: e es la carga del electrón
k es la constante de Boltzman
a₂ es un parámetro que permite realizar un mejor ajuste del modelo
a₃ es un parámetro relacionado con el potencial de excitación promedio de la lámpara

Donde: T₀ es la temperatura de la pared del tubo de descarga
a₄ es un parámetro relacionado con la conductividad térmica

Basados en los métodos de predicción de las frecuencias propias de una lámpara y confirmado por observaciones experimentales, la resistencia del arco de la lámpara ecuación (5), se puede representar como la suma de una resistencia determinada por la ecuación de Saha, que expresa la resistencia en estado estable del arco de descarga de la lámpara y una serie de coeficientes, dependientes de la frecuencia, que toman en cuenta la influencia de la resonancia acústica sobre dicha resistencia [12].

R en estado estable           Influencia de la RA
Donde: f es la frecuencia de operación de la lámpara
f_i es el conjunto de auto-frecuencias de la lámpara
a₅ es un parámetro relacionado con la resistencia de la lámpara
a₆ es un parámetro relacionado con el potencial de ionización promedio de la lámpara
A_i y B_i son vectores de constantes relacionadas con la influencia de los modos de resonancia acústica sobre la resistencia de la lámpara
K es la resistencia en estado estable de la lámpara

La corriente por la lámpara puede ser determinada en el circuito equivalente del sistema balasto-lámpara mediante la formulación de ley de Kirchoff de tensión ecuación (6).

Donde: v(t) es la tensión de alimentación de la lámpara
r es la resistencia equivalente del circuito formado por el balasto e ignitor de la lámpara
V_ele es la caída de tensión en los electrodos de la lámpara

Como hasta el momento no se cuenta con un modelo numérico de V_ele, en Wang (2008) se propone un modelo empírico que puede ser fácilmente implementado en software de diseño y que plantea dicha caída mediante la expresión de la ecuación (7), [13]. El mismo se desarrolla a partir de observaciones experimentales de la forma de onda de V_ele en lámparas especialmente diseñadas para estas mediciones.

Donde: A controla la amplitud de la señal
B controla la amplitud y la asimetría de la señal
C y D se obtuvieron mediante mediciones a diferentes frecuencias y aplicando técnicas de regresión lineal, al igual que A y B, resultando el sistema de ecuaciones lineales de la tabla 1.

La implementación del modelo se realiza con la herramienta Simulink de Matlab, auxiliados de funciones desarrolladas en ficheros del tipo m-file del propio software. En el modelo representado en la figura 2, aparecen delimitados en polígonos, los bloques que conforman las siete ecuaciones fundamentales del modelo. El polígono A contiene los bloques que modelan la ecuación de Vele, para obtener una forma de onda similar a la que describe [4]

En el caso del polígono C, encierra la parte del modelo correspondiente a la ecuación (1), y los tres términos P_in, P_con y P_rad de esta ecuación están desarrollados dentro de los bloques de funciones de igual nombre, delimitados por los recuadros D, E y F. El polígono B contiene los bloques que conforman la ecuación (6), en tanto el G contiene los bloques que dan lugar a la ecuación (5), cuya función Sumatoria de R, comprende el efecto de la resonancia acústica sobre la resistencia de la lámpara.

Para la realización de los experimentos se desarrolló una instalación experimental donde pudieran llevarse a cabo mediciones eléctricas a lámparas HID, operando en alta frecuencia. Se recolectaron datos de la lámpara trabajando en régimen estable, así como en presencia del efecto de la resonancia acústica, con el fin de poder realizar una adecuada identificación de los parámetros de la misma.Durante los experimentos se recopilan conjuntos de 2500 datos de una lámpara HPS de 70 W, para cada frecuencia de alimentación en intervalos de 50 Hz, en un rango de 2 a 18 kHz. Se realiza el análisis de los datos, mediante el cual se determina, que tanto la señal de excitación como las señales de salida, cuentan con la calidad requerida para las tareas de identificación.

Parametrización del modelo

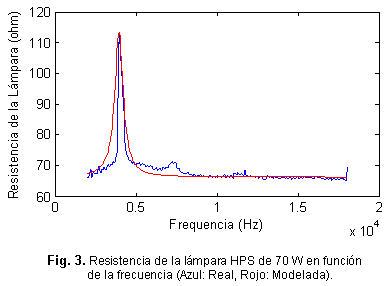
En esta etapa del modelado se ajustaron los valores de las constantes y parámetros del modelo. Con los valores recopilados de tensión y corriente de la lámpara, se calculó la resistencia equivalente de la misma para poder localizar las posibles zonas de resonancia acústica. Como resultado, 3,95 kHz es un punto de aumento significativo de la resistencia lo que hace suponer que a esta frecuencia la energía es suficiente para excitar el modo resonante en la lámpara. Esto se aprecia en la figura 3. Con este valor de auto-frecuencia (f_i) y otra frecuencia donde la lámpara opere en estado estable, se calculan las constantes a_i y b_i, de los respectivos vectores A_i y B_i de la ecuación (5), por métodos numéricos. El valor de ai es 2301847,5432, en tanto para bi se obtiene el valor 0,0212.

Con la obtención de estos valores de a_i y b_i, se completa el modelado de la resistencia de la lámpara, incluyendo el efecto de sus frecuencias propias y por tanto de la RA. Como se aprecia en la figura 3, el modelo converge adecuadamente con los valores reales de resistencia, por lo que el efecto de la RA sobre la resistencia de la lámpara está contenido en el modelo. El ajuste de los parámetros del modelo se realiza una vez determinadas sus ecuaciones y constantes y se implementa en Simulink. Con la ayuda del toolbox de optimización global basado en algoritmos genéticos [9], se define el vector de parámetros y se configura el algoritmo genético en la ventana de trabajo del mismo, acotando el intervalo del espacio de búsqueda y se imponen condiciones iniciales. En un fichero del tipo m-file de Matlab define la función objetivo de la ecuación (8). Función objetivo (@FO):

Al modelo se le imponen las siguientes condiciones iniciales: la temperatura de la pared del tubo de descarga de la lámpara (T₀), se fija en 1200 K, de acuerdo a lo expresado por Van Vliet (1986) para este tipo de lámparas HPS y la temperatura inicial de la lámpara que se ajusta a 4500 K [11]. El criterio de parada predominante del algoritmo de optimización es el número de iteraciones y se obtienen un óptimo de la función objetivo de 1,57905x10⁵. Los parámetros ajustados aparecen en la tabla 2.

Resolución del modelo

Una vez obtenidos todos los parámetros del modelo se llevan a cabo las simulaciones para una frecuencia de 9 kHz y con ello poder realizar el análisis de los resultados obtenidos, tanto gráficos como numéricos. Con la resolución del modelo se comprueba que las gráficas están en correspondencia con lo esperado, en cuanto a amplitud y forma de onda. La temperatura y la resistencia de la lámpara, resultados del modelo, también están en los valores y comportamientos similares al sistema real, como se muestra en la figura 4. Nótese que el valor de la resistencia es aproximadamente igual al valor correspondiente en el sistema real a 9 kHz que puede apreciarse en la gráfica de la figura 3.

Validación del Modelo

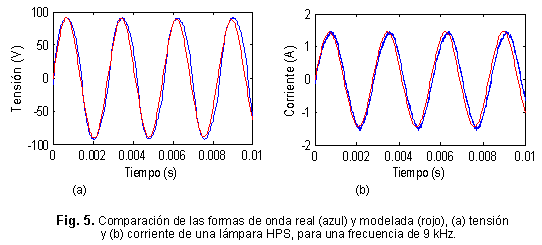
En la validación se utilizan varios criterios de los que se mencionan en [14]. El primero de ellos es la comparación gráfica de curvas, para apreciar la similitud entre las curvas reales de corriente y tensión con las obtenidas por el modelo. El conjunto de datos medidos a la frecuencia de 9 kHz, fue dividido en tres para su empleo en las etapas de parametrización, resolución y validación del modelo respectivamente. En la figura 5, se observan las formas de onda de tensión y corriente, tanto reales como del modelo para el intervalo de datos correspondiente a la validación, apreciándose una gran convergencia y poco desfasaje entre las formas de ondas reales y modeladas. La tensión del modelo muestra una amplitud ligeramente superior con respecto a los valores reales, pero en general el ajuste es bueno.

Otro método de validación que se utiliza es el de Validación Operacional, mediante el cual se determina si el modelo responde con suficiente aproximación al sistema real para el propósito requerido y en el dominio en que se pretende usar. Por ello se procede a la simulación en otros rangos de frecuencia de los cuales además se cuenta con datos reales y se comparan con la salida del modelo. En la figura 6, se muestran los resultados para la frecuencia de 15 kHz.

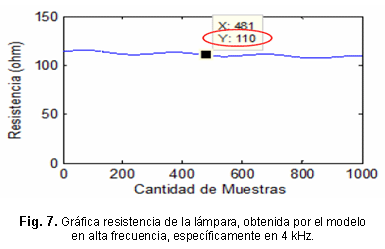
Como bien se puede apreciar, para esta nueva frecuencia, la respuesta del modelo también es bastante buena, el ajuste de las curvas es adecuado, las amplitudes de las formas de ondas de corriente y tensión que genera el modelo están acorde con la potencia de la lámpara HPS (70 W). En la forma de onda de tensión del modelo como en el sistema real, no aparecen los picos de reencendido de la lámpara por tratarse de operación en alta frecuencia. Otro resultado interesante acerca de la validación operacional del modelo de alta frecuencia, se encuentra en la curva de resistencia del arco de la lámpara, generada por el modelo para una frecuencia cercana a la frecuencia de resonancia de la lámpara de estudio (3,95 kHz). La figura 7, muestra que tal y como se esperaba, la resistencia de la lámpara en 4 kHz debe ser superior a 100 Ω, con una tendencia a ir disminuyendo en la medida que la frecuencia de operación continúe alejándose de la frecuencia de resonancia.

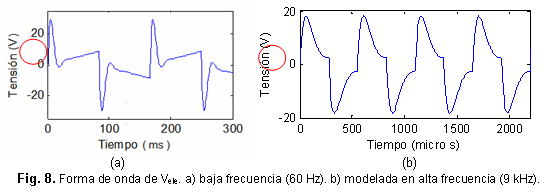
El comportamiento que tiene la forma de onda de V_ele para alta frecuencia, también valida operacionalmente al modelo. Según Yan (2005), en la medida que va aumentando la frecuencia de operación de la lámpara, el segundo máximo en cada semi-ciclo de la forma de onda de V_ele se va reduciendo, como se aprecia en la figura 8b, donde a diferencia de la forma de onda de V_ele de una lámpara a 60 Hz (figura 8a), el segundo máximo de cada ciclo, casi no existe [4].

Todas las simulaciones realizadas en el rango de frecuencias en que fueron recopilados los datos de tensión y corriente de la lámpara, arrojaron resultados similares de convergencia. El tercer método de validación implementado es el método estadístico, utilizando los criterios relacionados con el error cuadrático medio [10-14]. De esta forma se calcula el porcentaje de ajuste del modelo según la ecuación (9).

Porcentaje de ajuste del modelo

Donde: σ es la desviación estándar
y es la salida real
y_mod es la salida modelada
N es la cantidad de muestras

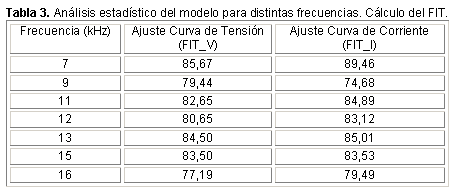
El índice FIT es reflejo de un buen modelo, cuando su valor es cercano a 100 % [10]. La tabla 3, muestra el resultado del cálculo del porcentaje de ajuste del modelo (FIT), para varias frecuencias de una lámpara HPS de 70 W, durante la etapa de validación. En todos los casos, los resultados sobrepasan el 70 % de ajuste, lo que constituye un buen ajuste para el modelo.

El valor medio del porcentaje de ajuste calculado para el modelo es de 85,6086 %, ya que los valores medios de los porcentajes de ajustes de las curvas de tensión y corriente modeladas, son de 84,4709 % y 86,7464 % respectivamente.Teniendo en cuenta los resultados que se obtienen de la validación del modelo se puede concluir que el mismo es perfectamente apto para el uso en el desarrollo de sistemas de control para las etapas de potencia de los balastos de alta frecuencia.

 

CONCLUSIONES

La metodología de modelado híbrido seguida posibilitó capturar la dinámica de resistencia, temperatura, tensión y corriente de las lámparas HID, específicamente de una lámpara HPS. Se construyó un modelo en Simulink a partir de las ecuaciones obtenidas del estudio del comportamiento de las lámparas, ajustándose sus parámetros mediante identificación experimental.Se logró validar el modelo para lámparas HPS. Las simulaciones y cálculos estadísticos realizados mostraron gran convergencia en los resultados gráficos entre el modelo desarrollado y el sistema real (lámpara HPS de 70 W), así como altos índices de ajuste, que como promedio fueron de alrededor de un 85 %.

Extender el modelado hacia las lámparas HPS, hace del modelo una herramienta de gran valor para los diseñadores de balastos electrónicos. Les permite trabajar en algoritmos que corrijan los fenómenos que ocurren en alta frecuencia en las lámparas, como es el caso de la resonancia acústica, pero también el envejecimiento de los parámetros eléctricos de la lámpara, desarrollando sistemas de control que mantengan la operación estable de las lámparas ante la presencia de estos fenómenos.

 

REFERENCIAS

1. CORREA GOMEZ, J.; et al., "Evaluation of close loop digital control based in a microcontroller and used to eliminate acoustic resonances in HID lamps in Power Electronics". Specialists Conference, 2004. PESC 04. 2004 IEEE 35th Annual (Volume:1 ) 2004, IEEE, p. 401-405 vol.1, doi: 10.1109/PESC.2004.1355779.

2. MAUSSION, P.; et al., "Acoustic Resonance Characteristics in a High Pressure Sodium Lamp". Industry Applications Society Annual Meeting, 2008. IAS '08. IEEE, p. 1-4 , 5-9, doi: 10.1109/08IAS.2008.232, ISSN 0197-2618.

3. BLANCO, C.; et al., "Comparison Between Different Discharge Lamp Models Based on Lamp Dynamic Conductance". IEEE Transactions on Industry Applications. 2011, vol.47, n.4, p. 1983-1991, doi: 10.1109/TIA.2011.2155014, ISSN 0093-9994.

4. YAN, W.; et al., "A universal PSpice model for HID lamps". IEEE Transactions on Industry Applications, 2005, vol.41, n.6, p. 1594-1602, doi: 10.1109/TIA.2005.857458, ISSN 0093-9994.

5. WAYMOUTH, J.F., "Electronic Discrage Lamps". The Massachusetts Institute of Technology Press, 1971, vol.2, 353 p., p. 2-9, p. 71-111, 187-200, ISBN: 0-262-23048-8.

6. JIANG, Y.; et al., "An adaptive acoustic resonance free electronic ballast for HID lamps". Industry Applications Conference, 2003, 38th IAS Annual Meeting Conference Record of the (Volume:2 ), 12-16 Oct. 2003, vol.2, p. 1020-1024, doi: 10.1109/IAS.2003.1257666, ISBN 0-7803-7883-0.

7. OSORIO, R.; et al., "Electric Dynamic Modeling of HID Lamps for Electronic Ballast Design". IEEE Transactions on Industrial Electronics, 2010, vol.57, n.5, p. 1655-1662, doi: 10.1109/TIE.2009.2033095, ISSN 0278-0046.

8. ZISSIS, G.; et al., "Modelling discharge lamps for electronic circuit designers: a review of the existing methods". Industry Applications Conference, 2001, Thirty-Sixth IAS Annual Meeting. Conference Record of the 2001 IEEE, vol.2, p. 1260-1262, doi: 10.1109/IAS.2001.955668, ISSN 0197-2618.

9. YAN, W.; et al., "Genetic algorithm optimised high-intensity discharge lamp model". Electronics Letters, 2002, IET, vol.38, p. 110-112, doi: 10.1049/el:20020O80, ISSN 0013-5194.

10. FERNANDEZ RODRIGUEZ, E.; et al., "Metodología para la obtención de modelos híbridos para el control". X Simposio Internacional de Automatización, Convención Internacional Informática 2011, 2011, La Habana, Cuba, ISBN: 978-959-7213-01-7.

11. VAN VLIET, J.A.J.M.; de GROOT, J.J., "The high-pressure sodium lamps". 1986, London: MacMillan Education LTD, 330 p., p. 13-29, 170-210, 208-225, 258-273, ISBN: 0-333-43245-2.

12. YAN, W.; HUI, S.Y.R., "An improved high-intensity discharge lamp model including acoustic resonant effect on the lamp arc resistance". IEEE Transactions on Power Electronics, 2004, vol.19, n.6, p. 1661-1667, doi: 10.1109/TPEL.2004.836628, ISSN 0885-8993.

13. WANG, W.; et al., "A physics-based model for HID lamps with rectifying effect". Vehicle Power and Propulsion Conference, 2008, VPPC '08. IEEE, 3-5 Sept. 2008, p.1-5, doi: 10.1109/VPPC.2008.4677755, ISBN: 978-1-4244-1849-7.

14. SARGENT, R.G., "Verification and validation of simulation models". Simulation Conference (WSC), Proceedings of the 2010 Winter, p. 5-8 , 166 ,183 , doi: 10.1109/WSC.2010.5679166.

 

 

Recibido: febrero de 2014
Aprobado: junio de 2014

 

 

Leonardo Cedeño Rodríguez, Ingeniero en Automática, Especialista en Automática, Empresa de Tecnología Médica Digital, La Habana, Cuba. e-mail: [e-mail]