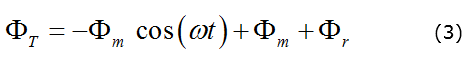APLICACIÓN DE LA COMPUTACIÓN

 

Medición de la corriente de inrush en transformadores de distribución

 

Measurement of inrush current in distribution transformers

 

 

Dr. C. T. Orestes Nicolás Hernández Areu, Dr. C. T. Josnier Ramos Guardarrama, Dra. C. T. Regla Perera Escobar

Centro de Investigaciones y Pruebas Electroenergéticas, CIPEL, Facultad de Ingeniería Eléctrica, Universidad Tecnológica de La Habana, José Antonio Echverría, Cujae, La Habana, Cuba.

 

 

---

RESUMEN

El fenómeno de la corriente de inrush es probablemente el proceso transitorio más común asociado a la explotación de los transformadores, debido a la habitual realización de maniobras de conexión y desconexión. Los valores elevados de corriente de inrush, pueden causar una serie de efectos nocivos tanto para el sistema eléctrico que lo alimenta como para el propio transformador, tales como caídas momentáneas de tensión, sobretensiones armónicas temporales, estrés electromecánico en los devanados, deterioro del aislamiento, etc. La característica “corriente de inrush – tiempo” de los transformadores es una información que los fabricantes deben brindar a los clientes, por lo que su medición es necesaria. En el presente proyecto se propone la utilización de un montaje de laboratorio relativamente simple y económico para la realización de esta medición, así como, el empleo de un software para el manejo y análisis de los resultados obtenidos.

Palabras clave: transformador, corriente de inrush, medición de la corriente de inrush.

---

ABSTRACT

The inrush current phenomenon is probably the most common transient process associated with the operation of transformers, due to the regular connection and disconnection manoeuvres. High values of inrush current can cause a series of adverse effects for both the electrical system that feeds to the transformer and the transformer itself, including momentary voltage drops, temporary harmonics surges, electromechanical stress in the windings, insulation deterioration, etc. The "inrush current - time" characteristic of the transformers is an usually requested information by the clients, that’s why it must be known and provided by manufacturers. In this project is proposed the use of a laboratory setup that is relatively simple and inexpensive to carry out this measurement, such as the use of software for managing and analyzing the results.

Key words: inrush current phenomenon, inrush current, measurement of inrush current.

---

 

 

INTRODUCCIÓN

Cuando un transformador es energizado, aplicando una tensión sinusoidal, inmediatamente fluye a través del devanado primario una corriente llamada corriente de excitación o vacío. La corriente de vacío alcanza una magnitud que es despreciable, frente a los valores de corrientes de trabajo del devanado por el cual circula.

En general, los materiales ferromagnéticos, tienen la propiedad de conservar cierto valor de flujo magnético o densidad de flujo una vez que se les retira la excitación, a este valor se le llama flujo residual o remanente, Ф_r y a la densidad de este flujo, densidad de flujo residual o remanente, B_r.

A pesar de que la magnitud de  la corriente de excitación es despreciable frente a la corriente de operación, en el momento de la energización, se produce un proceso transitorio que casi siempre tiene aparejado un crecimiento de esta corriente a  valores varias veces mayores que la corriente nominal de la máquina.

Esto es debido a que en estas condiciones la densidad del flujo magnético total en el núcleo del transformador excede el valor de densidad de flujo de saturación del mismo y el exceso de flujo restante tiene que circular por fuera del hierro.

En estas condiciones, el núcleo, se comporta como un núcleo de aire y la reactancia inductiva decrece a un valor extremadamente pequeño, produciéndose una sobrecorriente conocida como corriente de inrush.

Cuando el transformador se encuentra en vacío, este fenómeno es más severo que cuando la conexión se realiza estando la máquina con alguna carga.

La corriente de inrush puede definirse como una corriente transitoria de excitación, que se manifiesta como una corriente de carácter pulsante cuyo valor máximo, generalmente supera varias veces la magnitud de la corriente nominal de la máquina. Puede caracterizarse como la suma de dos componentes; una componente sinusoidal de estado estable y una componente transitoria y aperiódica de corriente directa que se atenúa en el tiempo a través de la inductancia y la resistencia del devanado energizado.

Estas corrientes, a su vez inducen flujos de estado estable (Ф) y transitorio. Como el flujo estable varía con el tiempo, en algún momento, se adiciona al flujo transitorio produciendo la saturación del núcleo magnético y si se tiene en cuenta, además, el flujo residual (Ф_r), puede darse el caso de un nivel de inducción magnética mayor a dos veces la inducción magnética de trabajo o estable del transformador.

 

MATERIALES y MÉTODOS

Corriente de inrush

La  corriente de excitación se presenta en todo el tiempo de funcionamiento del transformador, pero es medible únicamente estando el mismo en vacío a tensión y frecuencia nominal pues en operación normal se mediría junto con la corriente de carga, ante la cual es imperceptible [1].

Un ciclo completo de la tensión de excitación hará aparecer el lazo de histéresis del núcleo. Este lazo de histéresis tiene asociada una potencia activa, dicha potencia se calcula mediante el área que dicho lazo encierra. El cálculo teórico de esta potencia es complicado de realizar debido a que no se tiene una relación lineal entre la intensidad del campo magnético y la densidad de flujo, pero de manera experimental puede ser medido por medio de un wattímetro. Asumiendo que el transformador está en vacío, se puede garantizar que la corriente establecida a través de la bobina es la corriente de excitación. La ecuación que gobernará un flujo magnético total en el núcleo, está dada por:vea ecuaciones (1),(2),(3):

      

donde:
Ф_T: Flujo magnético total en el núcleo del transformador.
Ф_m: Amplitud del flujo magnético en el núcleo del transformador.
Ф_r: Flujo magnético residual en el momento de energización del transformador.
ω: Frecuencia angular.

Los términos constantes en la expresión anterior le dan un nivel de corriente directa (CD) a la señal de flujo, pero estos van decayendo debido a las pérdidas  haciendo que finalmente desaparezca dicha componente de directa.

Si se considera el flujo residual como nulo, el valor máximo se presenta cuando la señal de tensión va por el primer cruce por cero, es decir, cuando ωt = π, en esta situación el coseno de la expresión del flujo es -1 y por consiguiente el flujo total es máximo e igual al doble de la condición de amplitud para el flujo.

El establecimiento de este flujo máximo hace llegar al núcleo a la saturación por tanto establece altos niveles de fuerza magnética, la cual es proporcional a la tensión aplicada, generándose corrientes de magnitudes de hasta 8 y 10 veces el valor nominal. La situación empeora cuando el trasformador ya había sido energizado y se hace un recierre pues el flujo residual que tenía, hace aumentar mucho más el valor del flujo máximo, por tanto la corriente inrush del nuevo cierre llega inclusive a valores de 40 veces la corriente nominal dependiendo del diseño del transformador.

Si no existiese saturación en el núcleo, la corriente de magnetización variaría directamente proporcional al flujo, generándose una señal de corriente de magnetización sinusoidal y en fase con la señal sinusoidal del flujo, por lo tanto desfasada 90º con respecto a la señal de tensión aplicada.

Si la conexión de un transformador se realizara exactamente en el instante en que la onda de tensión aplicada corresponde con la densidad de flujo normal en su núcleo, esta energización tendría lugar sin transitorio alguno asociado. Sin embargo, en la práctica, la ocurrencia de un fenómeno transitorio en forma de un pico de corriente de energización o de inrush es inevitable, ya que el instante de la conmutación no es fácilmente controlable, y si el transformador es trifásico, el instante más favorable para la energización de una de las fases  no lo será para las dos restantes [2].

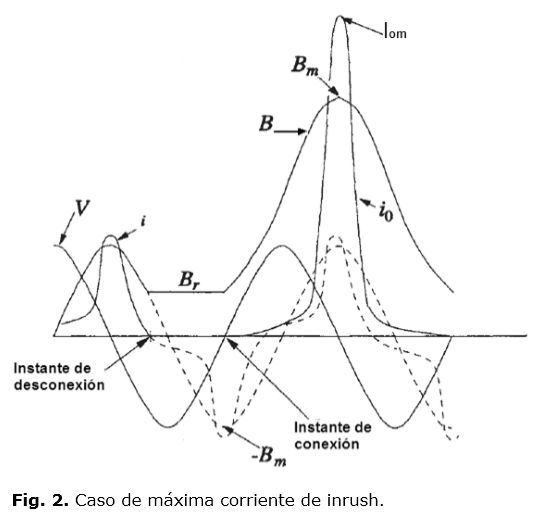
Cuando un transformador se desconecta, la corriente de excitación cae a cero siguiendo el lazo de la curva de histéresis, mientras que el valor de densidad de flujo cambia a un valor de densidad de flujo residual, Br, distinto de cero, como es evidente a partir de la curva de histéresis en la figura 1, (punto D).

El eje de ordenadas de la figura 1,  está en función del valor de flujo máximo, Ф_m, o densidad de flujo máximo, B_m. El eje de las abscisas está en función del valor de la corriente de vacío i_o, o la intensidad de campo magnético H. Para una densidad de flujo residual igual a B_r, se verifica un máximo también en la corriente de entrada cuando el transformador es reconectado en el instante en que la tensión aplicada es cero, como se muestra en la figura 2.

De acuerdo con el Teorema de Acoplamiento por Flujo Constante; el flujo magnético en un circuito inductivo no puede cambiar de repentinamente. El flujo, justo después de cerrar  el interruptor (en t = 0⁺) debe permanecer exactamente igual al flujo justo antes de haber cerrado el interruptor (en t = 0^- ). Por lo tanto, la densidad de flujo, en lugar de partir de su valor negativo máximo (-B_m), comenzaría desde Br, alcanzando un valor pico positivo de (B_r + 2B_m) conduciendo  a la saturación del núcleo.

Si el transformador se alimenta con una tensión sinusoidal de ecuación (4):

donde:
V_m: Amplitud de la tensión sinusoidal.
α: Ángulo de fase de la tensión en el momento de la energización.
I_o: Corriente de vacío.
R: Resistencia del  devanado energizado.
N: Número de vueltas del devanado energizado.
Φ(t): Flujo instantáneo.

Si se despeja dΦ(t), se integran ambos lados de la ecuación y se evalúa para las condiciones iniciales, t = 0 y Φ = ± Φ_r (en dependencia de la polaridad que tuvo el flujo en el momento de la desconexión), la solución en general de esta igualdad, como se muestra en la ecuación (5):

donde:
L: inductancia del devanado energizado.
t: instante de tiempo a partir de la conexión del transformador.

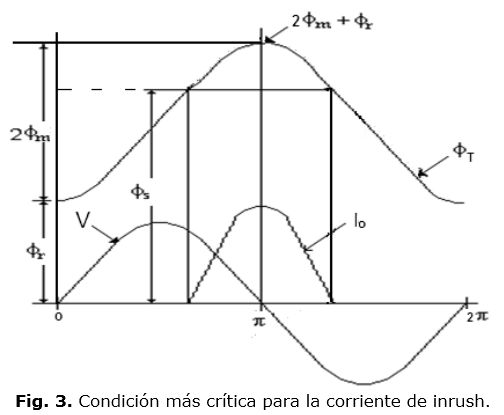
De acuerdo con la expresión anterior, la condición más crítica se verifica cuando coinciden las siguientes condiciones:

a) La conexión ocurre cuando la sinusoide de tensión cruza por cero,  es decir, para  α = 0. En esta condición en el segundo término de la ecuación, el cos (α) = 1

b) Para t = 8,33 ms, o sea, la mitad de un período de la señal de tensión, para este instante (ω_t) = π, cos (π + 0) = -1  y el primer término; - Ф_mcos (ω_t + α) = Ф_m.

También en estas condiciones; e^{- (R / L)} 0,008 ≈ 1 y el segundo y terceros términos, se hacen: Ф_mcos (α) e^{- (R / L)}  t = Ф_my ± Ф_re^{- (R / L)}  t = ± Ф_r

c) Cuando el flujo residual tiene el mismo signo que el flujo estable.

En estas condiciones el flujo total en el núcleo será; Ф_T  ≈ 2 Ф_m + Ф_r, como se muestra en las figuras 3 y 4. Obsérvese que  para t = 0: Ф_T = - Ф_m + Ф_m + Ф_r = Ф_r, es decir que en t = 0, el flujo en el núcleo es el residual.

La cantidad de flujo que exceda la magnitud de flujo de saturación del núcleo cerrará su camino por fuera del mismo. Es un flujo de dispersión y se puede obtener de acuerdo a la ecuación (6):

donde:
Ф_D: Magnitud del flujo de dispersión.
Ф_S: Magnitud del flujo de saturación.

Sustituyendo la ecuación (5) en (6), queda  la ecuación (7):

Y para la condición más crítica sería ver la ecuación (8):

La corriente necesaria para producir este flujo, es la corriente de inrush.

La forma de onda de corriente tiene una componente de corriente continua transitoria, que decae a la razón determinada por el cociente de la resistencia y la inductancia del devanado energizado (R/L), y una componente de corriente alterna (CA) en estado estacionario, -Ф_mcos (ω_t + α). La forma de onda típica de esta corriente en una fase para las condiciones más desfavorable, es mostrada en la figura 5.

Se puede observar que la forma de onda de corriente está completamente distorsionada en los primeros ciclos, en los cuales se han eliminado los semiciclos c negativos debido a que para estos, el valor de densidad de flujo es inferior al valor de saturación (resultando un valor muy pequeño de corriente). Por lo tanto, la corriente de entrada es altamente asimétrica y tiene una segunda componente armónica muy alta.

La constante de tiempo del circuito (L/R) no es tal constante, el valor de L cambia en función de la medida de la saturación del núcleo. Durante los primeros ciclos, la saturación es alta y el valor de L es bajo. Por lo tanto, la velocidad inicial de disminución de la corriente de entrada es bastante alta. Como las pérdidas amortiguan el circuito y el nivel de saturación decae, L aumenta retardando el decrecimiento. Por lo tanto, la disminución de la corriente de entrada comienza con una velocidad inicial alta y se reduce progresivamente; el fenómeno total posee una duración de unos pocos segundos. Los transformadores más pequeños tienen mayores velocidades de disminución de la corriente de inrush. En general, se puede decir que los transformadores con mayores pérdidas (menor eficiencia) tienen velocidades de disminución de corriente de inrush superiores.

Esfuerzos electromecánicos en transformadores causados por la corriente de inrush

Los valores pico de las corrientes de inrush máximas, se asemejan a los valores que pudieran esperarse para corrientes transitorias de cortocircuito. Sin embargo, las características de las tensiones mecánicas a causa del estrés electromecánico en  estos dos tipos de corrientes, son diferentes.

Mientras que la corriente de cortocircuito transitoria origina fuerzas que envuelven a cada uno los devanados del transformador que alimenta el cortocircuito, la corriente de inrush involucra solamente al devanado que está siendo energizado [3].

En la referencia [4] se muestra el resultado de las investigaciones sobre cómo las fuerzas electromecánicas producidas por corrientes de inrush en transformadores, se distribuyen en el interior de los devanados. Estos resultados demuestran que, con picos de corriente incluso un 30 % menor que los causados por corrientes de cortocircuito, las corrientes de inrush pueden producir fuerzas de niveles similares a las causadas por cortocircuito. Esto tiene su justificación en que la duración del transitorio asociado a la corriente de inrush es considerablemente mayor que el de la corriente de cortocircuito. Otro dato a tener en cuenta es que la presencia de corrientes de inrush es mucho más frecuente, ya que los eventos responsables de este fenómeno  forman parte de la operación habitual de cualquier sistema.

En la determinación de las fuerzas electrodinámicas bajo las condiciones de corriente de inrush solo son consideradas las componentes de los campos producidos por las corrientes en los conductores de la bobina primaria [5].

Las fuerzas electromagnéticas tienen una forma general de acuerdo con la ecuación (9), sobre la base de la fuerza de Lorentz [6].

donde:
F: Es la densidad  volumétrica de la fuerza magnética, [N/m²].
J: Es la densidad superficial de corriente, [A/m²].
B: Es la densidad del flujo magnético de dispersión, [T].

Factores que afectan al fenómeno de inrush

Dentro de los parámetros del propio transformador el factor más influyente  en la magnitud de la corriente de inrush el número de espiras del devanado, seguido de la inducción magnética y las características geométricas del molde de las bobinas [7].

Las características geométricas del núcleo del transformador: ancho de la columna, ancho y altura de la ventana, no juegan un papel significativo en la magnitud de la corriente inrush.

Además hay varios los factores externos al transformador que afectan el fenómeno de la corriente de inrush, estos son:

1. Instante en que se conecta el transformador. La corriente de inrush decrece a medida que aumenta el ángulo de la onda de tensión. Es máxima para α = 0 ° y mínimo cuando α = 90 °.

2. El magnetismo residual que quedó en el transformador cuando se desconectó.

Corriente de inrush es agravada significativamente por la densidad de flujo residual, la cual depende de las características del material de núcleo y el factor de potencia de la carga del transformador en el instante en que se apagó. El instante de la desconexión tiene un efecto sobre la densidad de flujo residual dependiendo del tipo de carga.

3. La resistencia de la línea entre la subestación y el transformador reduce la corriente y acelera su velocidad de decaimiento.

4.  Cuando el transformador es conectado a una carga cuyo factor de potencia es bajo (ya sea inductivo o capacitivo), el pico de corriente es mayor.

 

RESULTADOS Y DISCUSION

Medición de la corriente de inrush

Para la operación es importante conocer los valores pico de la corriente de inrush en los primeros ciclos, o bien, estimar el tiempo que esta demorará en caer a un valor igual a la corriente de vacío normal. Son conocidos varios métodos [4, 5, 6, 8, 9]  para  obtener la solución analítica o simulación numérica, pero su obtención experimental es una práctica muy útil.

Para realizar su medición es necesario garantizar que esta se realice en la peor condición para la ocurrencia del inrush, por lo cual hay que utilizar un interruptor sincrónico con detector de cruce por cero para el control del ángulo de conexión.
Para la determinación exacta del flujo residual se empleó el procedimiento descrito en [10].

En la figura 6 se muestra el esquema de medición, compuesto por:

• Un transformador de 367 kVA como fuente de alimentación.
• Un interruptor general para la energización del circuito.
• Un interruptor magnético para la conexión y desconexión del transformador bajo prueba.
• El interruptor sicrónico a tiristores.
• Una resistencia shunt para la medición de la corriente.
• Transformador de potencial para la captación de la tensión y la corriente.
• Un osciloscopio.

La figura 7, muestra la medición de la corriente de vacío de un transformador en estado estable. El oscilograma muestra como ante una tensión sinusoidal la corriente no es sinusoidal con un alto contenido de armónicos.

Como el instante en que se conecta el transformador es importante en la magnitud de la corriente, siendo el momento más inoportuno cuando la tensión cruza por cero, es necesario emplear un interruptor sincrónico que automáticamente cierre en el momento en que el operario decida y así poder hacerlo en el cruce por cero.

A continuación se muestran varias mediciones de corriente de inrush realizadas a transformadores de distribución por sus devanados de baja tensión para distintos instantes de energización a partir del cruce por cero de la tensión. Vea figuras 8, 9, 10 y 11.

 

CONCLUSIONES

• El tiempo en que se verifica el primer pico de la corriente de inrush, es independiente de la potencia del transformador.
• El transitorio en las mediciones realizadas desaparece, prácticamente entre los 60 ms y  los 120 ms.
• Para iniciar el proceso de captación de las señales, es aconsejable utilizar una escala de amplitud del mayor rango posible y a partir de la magnitud del primer pico de corriente obtenido, ajustar esta escala al valor apropiado.
• El ajuste de la escala de tiempo para mayor visibilidad del fenómeno debe ser de 10 o 20 ms/división.

 

REFERENCIAS

1. Cazacu E. et al. Transformer inrush current predetermination for distorted waveform voltage supply. Rev. Roum. Sci. Techn.–Électrotechn. et Énerg. 2013;58(3):243-251.

2. Cazacu, E. et al. An improved method for the inrush current evaluation in single phase power transformers. 8th International Symposium on Advanced Topics in Electrical Engineering (ATEE). IEEE. 2013. pp. 1-6.

3. R. Guimarães AC. at al. Investigação sobre Estresses Eletromecânicos em Transformadores Causado pela Corrente de Energização (Inrush). IEEE/PES Transmission and Distribution Latin America. Sao Paulo, Brasil. 2010.

4. NegaraI. MY. et al. Materials and Cutting Method Effects of Three Phase Transformer-Core on Magnetization Curve and Inrush Current: Simulation Approach. International Review on Modelling and Simulations (IREMOS). 2015;8(3):370-376.

5. Taghikhani MA. et al. Harmonic Modeling of Inrush Current in Core Type Power Transformers Using Hartley Transform. Iranian J. Elect. Elect. Eng. 2015;11(2):174-183.

6. Jamali M. Calculation and Analysis of Transformer Inrush Current Based on Parameters of Transformer and Operating Conditions. Elektronika ir Elektrotechnika. 2011;109.(3):17-20.

7. Singh PK., Chaturvedi DK. Neural Network Based Modeling and Simulation of Transformer Inrush Current. International Journal of Intelligent Systems and Applications; 2012;4(5):1-2.

8. CHIESA, N. et al. Calculation of Inrush Currents–Benchmarking of Transformer Models. En: IPST Conference, Delft, The Nederlands. 2011.

9. Jazebi S., De Leon F., Wu N. Enhanced Analytical Method for the Calculation of the Maximum Inrush Currents of Single-phase Power Transformers. IEEE Transactions on Power Delivery. 2015;30(6):2590-2599.

10. Moses PS., Masoum MA., Moghbel M. Effects of Iron-core Topology on Inrush Currents In Three-phase Multi-leg Power Transformers. In: IEEE Power and Energy Society General Meeting. 2012.  p. 1-6.

 

 

Recibido: septiembre de 2016
Aprobado: enero de 2017

 

 

AUTORES

Orestes Hernández Areu. Ingeniero Electricista, Doctor en Ciencias Técnicas. Investigador Titular del Centro de Investigaciones y Pruebas Electroenergéticas (CIPEL), Facultad de Ingeniería Eléctrica, Universidad Tecnológica de la Habana José Antonio Echeverría, Cujae, La Habana, Cuba.
E-mail: [e-mail]