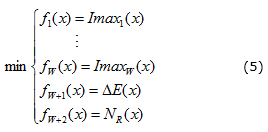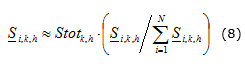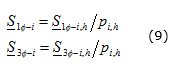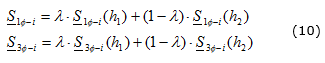APLICACIONES INDUSTRIALES

Balanceo de Fases en Circuitos de Distribución de Santa Clara

 

Phase-balancing in distribution circuits of Santa Clara

 

 

Dr. CT. Ignacio – Pérez Abril, Reinier – Herrera Casanova, Omar – Álvarez Fleites

Universidad Central Marta Abreu, de Las Villas, Santa Clara, Cuba.

 

 

---

RESUMEN

Los sistemas de distribución primaria contienen asimetrías en los circuitos ramales y en las cargas que son la fuente del desequilibrio de las corrientes de fase. Este trabajo define el problema de balanceo de fases como la minimización de tres objetivos: el desequilibrio máximo de corriente en puntos seleccionados del circuito para todas las posibles condiciones de funcionamiento; las pérdidas en los conductores del alimentador primario; y el número de reconexiones necesarias para alcanzar los dos objetivos anteriores. Para resolver este problema se ha desarrollado una aplicación de Matlab basada en el algoritmo genético de clasificación no dominada. El programa de optimización se complementa con una aplicación desarrollada para estimar las cargas del circuito a partir de las mediciones disponibles. Los resultados obtenidos en cinco circuitos de distribución de la ciudad de Santa Clara se presentan para mostrar las ventajas del enfoque presentado.

Palabras clave: sistemas de distribución, algoritmo genético, optimización, balanceo de fases.

---

ABSTRACT

Primary distribution systems contain asymmetries in the lateral circuits and in the loads that are the source of the phase current unbalance. This work defines the phase balancing problem as the minimization of: the maximum current unbalance at selected points in the circuit for all possible operating conditions; the losses in the conductors of the primary feeder; and the number of reconnections required to achieve the two previous objectives. To solve this problem we have developed a Matlab application based on the non-dominated sorting genetic algorithm. The optimization program is complemented with an application developed to estimate the loads of the circuit from the available measurements. The results obtained in five circuits of distribution of the city of Santa Clara are presented to show the advantages of the presented approach.

Key Words: distribution systems, genetic algorithm, optimization, phase balancing.

---

 

 

INTRODUCCIÓN

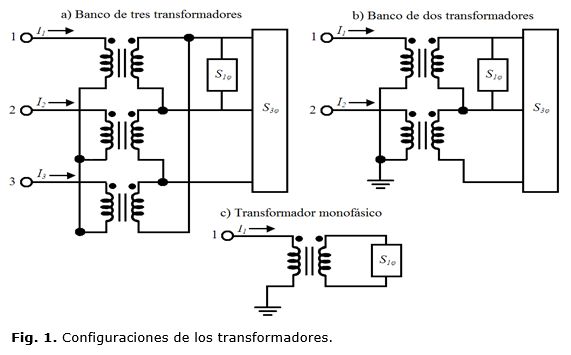
Los sistemas de distribución de media tensión están compuestos por una sección de tres fases y neutro que puede extenderse mediante varias secciones ramales de dos fases y neutro o de una fase y neutro. Las cargas monofásicas se suministran mediante transformadores monofásicos conectados entre fase y neutro, mientras que las cargas mixtas trifásicas y monofásicas son suministradas por bancos de tres transformadores o por bancos de dos transformadores. Estas asimetrías son la fuente del desequilibrio de las corrientes de fase a través de toda la extensión de estos circuitos.

Si existe un desequilibrio excesivo de las corrientes de fase en funcionamiento normal, la corriente de desequilibrio puede interpretarse como una corriente de falla a tierra por las protecciones correspondientes. Se pueden colocar varios interruptores en diferentes secciones del circuito, así como en las interconexiones entre diferentes circuitos. Por lo tanto, el desequilibrio máximo de corriente en cada uno de estos conmutadores debe minimizarse considerando todas las condiciones operativas que pueden cambiar la topología de red.

Por otro lado, los desequilibrios de corriente provocan el incremento de las pérdidas en los conductores de fase. Incluso en un circuito que está equilibrado en su extremo de origen, estas pérdidas pueden ser altas si el circuito está desequilibrado a través de su extensión.

El problema del balance de fases consiste en la reconexión de algunos elementos (circuitos ramales o transformadores de distribución) para mejorar el equilibrio de las corrientes de fase y reducir las pérdidas en los circuitos de distribución de media tensión. El número de elementos a reconectar debe ser mínimo.

Gupta [1] introduce una estrategia para balancear las corrientes de fase del circuito y reducir a la mitad la corriente de neutro mediante la reconexión de los devanados de los transformadores de dos devanados. Posteriormente extiende su estrategia de balanceo en [2] mediante el uso de un transformador balanceador en lugar de modificar las conexiones de los transformadores de distribución existentes.

Por su parte hoosmand y soltani [3, 4] implementan el balance de las fases utilizando los métodos: optimización por enjambre de partículas, forraje de bacterias y técnicas difusas. La función multiobjetivo a minimizar considera: la corriente de neutro, el costo de las labores de reconexión, las caídas de tensión y las pérdidas en las líneas.

Fei [5] investiga el uso de simulación del recocido caótica, mientras que sathiskumar [6] emplea un método de evolución diferencial auto-adaptiva y mahendran [7] un algoritmo heurístico híbrido. Seis algoritmos se reportan por wang, skiena y robertazzi [8], que concluyen proponiendo la programación dinámica para el problema de balanceo.

Schweickardt [9] utiliza una implementación evolucionaria y difusa para la optimización por enjambre de partículas para alimentadores de baja tensión,  mientras que boroujeni [10] utiliza un método heurístico dinámico con igual fin.

Finalmente, padarbinda [11] utiliza la evolución diferencial para proyectar el balanceo óptimo y seleccionar los conductores de un circuito. Solo considera la corriente de neutro total dentro de sus objetivos.

En resumen, se han aplicado varios métodos para resolver el equilibrio de fases. Sin embargo, no todos los enfoques consideran todas las condiciones pertinentes ni utilizan técnicas eficientes de optimización multiobjetivo que permitan la obtención de la frontera de pareto del problema.

Varias contribuciones [12-14] se han dedicado a resolver el problema de equilibrio de fases mediante el algoritmo genético de clasificación no dominada (nsga-ii). En cada nueva contribución se han agregado nuevas posibilidades al programa de optimización cuyos resultados se presentan en este trabajo.

El problema de balanceo de fases se define aquí como la minimización de: 1) el desequilibrio máximo de corriente en puntos seleccionados del circuito para todas las posibles condiciones de funcionamiento; 2) las pérdidas en los conductores del alimentador primario; y 3) el número de reconexiones necesarias para alcanzar los dos objetivos anteriores.

El programa de optimización se complementa con una aplicación desarrollada para estimar las cargas del circuito a partir de las mediciones disponibles. Los principios de este método de estimación se describen en el trabajo.

La metodología de balanceo comprende: 1) el celaje detallado de los circuitos y la estimación de los gráficos de carga a partir de las mediciones disponibles en la subestación; 2) la determinación de las variantes de balanceo mediante el programa de optimización; y 3) la ejecución de la variante de balanceo seleccionada y la evaluación de sus resultados a partir de las mediciones.

En este trabajo se presentan los resultados obtenidos tras aplicar esta metodología en cinco circuitos de distribución de la ciudad de santa clara. Estos resultados demuestran las ventajas del enfoque presentado.

 

MATERIALES Y MÉTODOS

Problema de optimización

Los bancos de transformadores trifásicos y los transformadores monofásicos son responsables de suministrar las cargas monofásicas de 120/240 V (S1φ) y las cargas trifásicas de 240 V (S3φ) como se muestra en la figura 1

Las potencias complejas S1, S2 y S3 de los transformadores conectados en las fases del circuito primario están determinadas por las cargas de baja tensión como se indica en las expresiones de la tabla 1.

La tabla 2 presenta las posibles conexiones de los terminales primarios 1, 2, 3 de los elementos que pueden ser reconectados (ramales y transformadores) según las fases disponibles en el circuito primario. Las conexiones de los circuitos ramales modifican las fases a las que están conectados los transformadores colocados en estos ramales.

Variables independientes

Para equilibrar las fases del circuito se debe determinar el conjunto de elementos que deben reconectarse y sus nuevas conexiones. Si el parámetro Nc definido por el usuario es el número máximo de reconexiones en el circuito, se definen los dos vectores xvar y xcon de Nc elementos de tal manera que el vector xvar determina el conjunto de elementos reconectados mientras que el vector xcon representa las nuevas conexiones para estos elementos (tabla 2).

*La posición de cada fase corresponde con los terminales 1, 2 y 3 en cada caso.

La ecuación (1),  define el vector x de variables independientes del problema, formado por los subvectores: x_var y x_con.

Funciones objetivo

La matriz Iabc(3xNx24) representa las corrientes de fase en los terminales primarios de todos los N nodos del circuito para el ciclo de carga de 24 h. Las corrientes de los bancos de transformadores trifásicos y los transformadores monofásicos se determinan utilizando las potencias de fase de la tabla 1, dadas las conexiones de los elementos del circuito. Es decir, Iabc es una función de x.

Se considera que la red de distribución contiene varios interruptores que pueden ser operados para obtener: un estado de funcionamiento normal (t = 0) y varios estados de contingencia  (t = 1...S) de la red. En todos los estados el circuito resultante es radial.

Dadas las corrientes de carga Iabc(x), el vector de las corrientes de fase I_i,h(x,t) en la rama i a la hora h se determina como la suma de las corrientes de fase de las cargas conectadas al conjunto C_i(t) de los nodos suministrados por esta rama en el estado t, según la ecuación (2).

Después de obtener las corrientes de fase en todas las ramas y estados de operación, se puede calcular la corriente de neutro In_i,h(x,t) así como las pérdidas de potencia ΔP_i,h(x,t) en cada rama i y estado t.

Para lograr el correcto funcionamiento de las protecciones de falla a tierra en todas las condiciones, se debe minimizar la corriente de neutro máxima Imax_k(x), vea la ecuación (3), en cada rama i (k) donde se coloca un desconectivo k.

Por otro lado, sólo deben determinarse las pérdidas de energía ΔE(x) según la ecuación (4), en el estado de funcionamiento normal, porque las contingencias son de corta duración y se producen esporádicamente.

Si se considera la minimización de las corrientes de neutro en W ramas del circuito, y NR(x) representa el número de elementos reconectados, el problema de optimización multiobjetivo se establece, según la ecuación (5), como:

Método de optimización

La aplicación desarrollada para optimizar esta formulación se basa en el algoritmo de optimización multiobjetivo NSGA-II que puede minimizar simultáneamente varios objetivos conflictivos. Para implementar esta aplicación se ha utilizado el código de Matlab ofrecido por Sheshadri [15], que emplea un cromosoma codificado en números reales. El código original de los operadores genéticos ha sido ligeramente modificado para incluir el cruce y la mutación de variables de tipo entero. Cada vez que se produce una nueva solución x por cruce o por mutación, el algoritmo NSGA-II emplea una función para evaluar todas las funciones objetivo del problema (5). En esta implementación, la función referida considera la tensión nominal en todos los nodos para evaluar las corrientes de fase Iabc(x) en los nodos y luego determina los valores de las funciones objetivo.

Estimación de las cargas

Para optimizar el balance de las fases del circuito, se debe determinar la variación diaria de las corrientes de fase Iabc de todas las cargas del circuito. Esto implica la determinación de la variación diaria de las cargas S1φ monofásicas y S3φ trifásicas en el devanado secundario de todos los transformadores trifásicos y transformadores monofásicos de distribución.

Normalmente, la estimación de estas cargas se realiza considerando patrones de carga diarios típicos de diversas clases de clientes (residenciales, comerciales, industriales, etc.) que se determinan mediante análisis estadístico de las cargas de la distribución.

Estas cargas deben ser estimadas porque normalmente no existen mediciones registradas de las mismas. Para el estado normal (t = 0), el patrón de variación diaria de la suma de las corrientes de fase de todas las cargas (dadas sus conexiones iniciales) debe reproducir con cierta precisión el patrón de variación diaria típica de las corrientes totales medidas en las fases y en el neutro del circuito.

Suponiendo que cada carga de distribución del circuito cumple con uno de los patrones de carga típicos, si se determinan los valores máximos de estas cargas, la variación diaria de la suma de todas las cargas debe aproximarse al patrón medido característico del circuito.

Cuando no se dispone de otros datos, las cargas se pueden estimar sobre la base de la potencia nominal de los transformadores de distribución presentes en el circuito. Una estimación aproximada de la potencia aparente a la hora h, S_i,k,h del transformador de distribución i que está conectado en la fase k puede obtenerse por la ecuación (6):

donde: Stotk,h es el módulo de la potencia aparente total medida en la fase k del circuito a la hora h, y Strf_i,k es la potencia nominal del transformador de distribución i que está conectado en la fase k. Sin embargo, las potencias aparentes por fase, S1, S2 y S3 de cada tipo de banco de transformadores están determinadas por las cargas S1φ y S3φ tal como se dan en las expresiones de la tabla 1. Si ambas cargas tienen igual factor de potencia, puede determinarse la relación  α = |S1φ|/|S3φ| que asegure un factor de carga igual en todos los transformadores del banco. La tabla 3, muestra las expresiones para calcular el módulo de la potencia aparente de dichas cargas.

Algoritmo de estimación

Para cada carga i, existe un gráfico de carga típico p_i, tal que p_i,h es la carga a la hora h (en por unidad de la carga máxima). De esta forma, si el transformador en el nodo i alcanza su máxima carga a alguna hora diferente de h, la potencia esperada de dicho transformador en la fase k y la hora h, S_i, k, h₀ se calcula mediante la ecuación (7), donde Φ es el ángulo del factor de potencia de la carga total del circuito:

El algoritmo de estimación de las cargas a la hora h comienza con esta aproximación inicial de las potencias en los transformadores (7), y mientras el error entre el módulo de la suma de todas las potencias estimadas por fase S_i,k,h y la carga total medida por fase Stotk,h sea mayor que el error aceptado, se ejecutan los siguientes pasos:

1. Se obtiene una nueva estimación de las potencias en los transformadores S_i,k,h mediante la ecuación (8):

2. Se obtienen las cargas estimadas de baja tensión S_1φ-i,h y S_3φ-i,h utilizando las ecuaciones de la tabla 3.

3. Se obtienen nuevas estimaciones para las potencias S_i,k,h que corresponden a las cargas S_1φ-i,h y S_3φ-i,h mediante las expresiones de la tabla 1.

Cuando el lazo termina, las cargas máximas S_1φ-i yS_3φ-i en los nodos se calculan mediante las ecuaciones (9):

Utilizando el algoritmo de estimación presentado, se estiman las cargas en las horas del pico del mediodía (h₁) y del pico nocturno (h₂) y entonces, el valor final de las cargas estimadas se obtiene como una combinación lineal de dichos estimados mediante la ecuación (10):

donde: λ es un escalar que se obtiene minimizando por mínimos cuadrados los errores entre el patrón estimado y medido para las corrientes de fase.

Si se escogen adecuadamente los gráficos de carga, este procedimiento realiza una estimación de las cargas de los transformadores que dan lugar a un gráfico de carga de las corrientes totales por fase muy semejante al medido.

 

RESULTADOS Y DISCUSIÓN

Como un ejemplo de la efectividad del procedimiento que se presenta, en 2016 se realizó el balanceo de cinco circuitos de la ciudad de Santa Clara, en particular los circuitos: 1, 3, 31, 32 y 169 cuyos datos generales se ofrecen en la tabla 4.

El celaje de estos circuitos se realizó en todo detalle y se estimaron las cargas y gráficos de carga necesarios utilizando el programa de estimación desarrollado al efecto. En este paso se comprobó que una selección incorrecta de los gráficos o una inexacta representación del circuito conducen a grandes errores en la estimación de las cargas y provocar respuestas erróneas del programa de optimización. Todo el trabajo de balanceo de estos circuitos se coordinó con la Dirección Técnica de la Empresa Eléctrica en Santa Clara. A solicitud de estos especialistas se consideró solo la reconexión de los ramales de dos o de una fase, pues de esta forma se facilitaban las labores de reconexión. En todos los circuitos con excepción del 169, se consideró solo la minimización de la corriente de neutro total, mientras que en el circuito 169 se minimizaron tres corrientes de neutro simultáneamente, la corriente de neutro total y las corrientes de neutro en los dos desconectivos S1 y S2 que existen en el tronco del circuito.

Una vez realizada la optimización de los circuitos con los parámetros seleccionados, el programa de optimización obtuvo un conjunto de soluciones para cada circuito (figura 2), de donde se escogieron las soluciones a aplicar.

En el circuito 169 se escogió una solución con seis cambios de conexión en ramales como se muestra en la propia figura 2. Como se puede visualizar en la figura 3, estos cambios se distribuyen en las tres secciones en que se divide el circuito y afectan un gran conjunto de cargas.

Las variantes escogidas para balancear los circuitos fueron aplicadas por el personal técnico de la Empresa Eléctrica en el mes de mayo de 2016.

El efecto real de estas variantes se comprueba en la figura 4, que muestra las mediciones de las corrientes de fase y de neutro registradas en la semana en que se realizó el balanceo en los circuitos. En cada caso puede determinarse el día en que se ejecutó la reconexión de los ramales por la desconexión del circuito en el horario de los trabajos.

En forma general se observa (figura 4), el efecto muy positivo de las variantes aplicadas sobre el balance de las corrientes de fase y sobre la reducción de la corriente de neutro en todos los circuitos (solo se mide la corriente de neutro total).

La tabla 5, realiza una comparación del comportamiento de varios indicadores del desbalance máximo antes y después de realizado el trabajo de balanceo. Estos indicadores se han determinado a partir de las mediciones efectuadas en dichos circuitos (figura 4) y son valores máximos para los cuatro días previos al balanceo (antes) y los cuatro días posteriores (después). Esta comparación comprueba numéricamente los beneficios obtenidos y permite evaluar en qué casos se obtuvieron los mejores resultados.

El otro resultado obtenido con las acciones de balanceo consiste en los ahorros de energía que se logran por la reducción de las pérdidas en los conductores primarios. Estos ahorros no pueden ser comprobados y solo se determinan por la diferencia entre las pérdidas de energía inicial y final que ofrece el propio programa de optimización.

La tabla 6, muestra los ahorros estimados, así como el costo de las labores de balanceo según se reportó por los operarios a cargo de este trabajo.

Este ahorro de energía representaría unos 63 MWh en un año que tienen que generarse en plantas que utilizan fundamentalmente combustible fósil. Este ahorro supera con creces el exiguo costo de las acciones de balanceo.

 

CONCLUSIONES

Los resultados obtenidos con la aplicación de la metodología presentada a varios circuitos de distribución de la ciudad de Santa Clara permiten llegar a las siguientes conclusiones:

1. Es muy importante lograr una buena representación de los circuitos y sus cargas, lo que implica un celaje minucioso, así como la correcta caracterización de los gráficos de carga.

2. El algoritmo de estimación de carga brinda resultados satisfactorios, aunque para mejorar sus resultados deben incorporarse otros datos adicionales sobre las cargas, como una posible estimación inicial de las cargas de los transformadores a partir de tomas de carga o criterios de los técnicos.

3. El programa de optimización calcula muchas soluciones alternativas que permiten al ingeniero ejercer su criterio al escoger la solución a aplicar.

Una posible dirección para el trabajo futuro consiste en incorporar al problema los análisis de probabilidades para determinar cuáles de las soluciones calculadas tienen un error probable menor al considerar las incertidumbres en la estimación de las cargas.

 

REFERENCIAS

1. Gupta N., Swarnkar A, and Niazi K.R. A novel strategy for phase balancing in three-phase four-wire distribution systems, IEEE Power and Energy Society General Meeting, San Diego (CA). 2011; p. 1-7. ISBN  978-1-4577-1002-5.

2. Gupta N., Swarnkar A. and Niazi K.R. A novel method for simultaneous phase balancing and mitigation of neutral current harmonics in secondary distribution systems. International Journal of Electrical Power & Energy Systems. 2014;55(1):645-656. ISSN 0142-0615.

3. Hooshmand RA. and Soltani SH. Fuzzy Optimal Phase Balancing of Radial and Meshed Distribution Networks Using BF-PSO Algorithm. IEEE Transactions on Power Systems. 2012;27(1):47-57. ISSN 0885-8950.

4. Hooshmand RA. and Soltani, SH. Simultaneous optimization of phase balancing and reconfiguration in distribution networks using BF–NM algorithm. International Journal of Electrical Power & Energy Systems. 2012;41(1):76-86. ISSN 0142-0615.

5. Fei, Chun Guo. Solving Load Phase Balancing Problem in LV Distribution Networks by Chaotic Simulated Annealing. Advanced Materials Research. 2012;463(1):689-693. ISSN 1662-8985.

6. Sathiskumar M., Lakshminarasimman L. and Thiruvenkadam S. A self adaptive hybrid differential evolution algorithm for phase balancing of unbalanced distribution system. International Journal of Electrical Power & Energy Systems. 2012;42(1):91-97. ISSN  0142-0615.

7. Mahendran G., Sathiskumar M., Thiruvenkadam S. and Lakshminarasimman L. Multi-objective Unbalanced Distribution Network Reconfiguration through Hybrid Heuristic Algorithm. Journal of Electrical Engineering & Technology. 2013;8(2):215-222. ISSN 1975-0102.

8. Wang K., Skiena S. and Robertazzi TG. Phase balancing algorithm. Electric Power Systems Research. 2013;96(1):218-224. ISSN 0378-7796.

9. Schweickardt G., Gimenez Alvarez JM and Casanova C. Metaheuristics approaches to solve combinatorial optimization problems in distribution power systems. An application to Phase Balancing in low voltage three-phase networks. International Journal of Electrical Power & Energy Systems. 2016;76(1):1-10. ISSN 0142-0615.

10. Taghipour Boroujeni S., Mohammad M., and Zhale H. A Dynamic and Heuristic Phase Balancing Method for LV Feeders. Applied Computational Intelligence and Soft Computing 2016. 2016;(1):1-8. ISSN 1687-9732.

11. Samal P., Sanjib G., and Sanjeeb M. Planning of unbalanced radial distribution systems using differential evolution algorithm. Energy Systems. 2016;1-22. ISSN 1868-3967.

12. Pérez Abril, I., “NSGA-II phase balancing of primary distribution circuits by the reconnection of their circuit laterals and distribution transformers”, Electric Power Systems Research, 2014, vol. 109, n. 1, p. 1–7. ISSN 0378-7796.

13. Pérez Abril, I. Optimización multiobjetivo del balance de fases en circuitos de distribución primaria. Ingeniería Energética. 2016;37(2):84-93. ISSN 1815-5901

14. Pérez Abril I. Multi-objective optimization of the balancing of phases in primary distribution circuits. International Journal of Electrical Power & Energy Systems. 2016;82:420-428. ISSN  0142-0615.

15. Aravind S. NSGA-II source code available [consultado en octubre del 2012].Disponible: http://www.mathworks.com/matlabcentral/fileexchange/10429-nsga-ii-a-multi-objective-optimization-algorithm/content/NSGA-II/

 

 

Recibido: enero de 2017      
Aprobado: junio de 2017

 

 

AUTORES

Ignacio Pérez Abril. Ingeniero Electricista, Doctor en Ciencias Técnicas, Profesor Titular, Director del Centro de Estudios Electroenergéticos CEE. Universidad Central Marta Abreu, de Las Villas, Santa Clara, Cuba.
 e-mail: [e-mail] 

Reinier Herrera Casanova. Ingeniero Electricista, Graduado en Adiestramiento, Departamento de Eléctrica. Universidad Central Marta Abreu, de Las Villas, Santa Clara, Cuba.
e-mail: [e-mail]

Omar Alvarez Fleites. Ingeniero Electricista, Graduado en Adiestramiento, Departamento de Eléctrica. Universidad Central Marta Abreu, de Las Villas, Santa Clara, Cuba.
 e-mail: [e-mail]