Artículo Original

Disipadores de energía - parte VII: trampolín o salto en esquí

Energy dissipation - part VII: ski jump hydraulics

Rafael Pardo Gómez¹ 

¹Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). La Habana, Cuba

RESUMEN

El presente artículo es el séptimo de una serie de siete, todos relativos a los disipadores de energía que se pueden emplear en obras hidráulicas. Todos estos artículos en su conjunto conforman una monografía que sobre este tema desarrolló el autor, concluyéndola a mediados del año 2017 y posteriormente incorporándola a una nueva edición - en preparación - del libro de texto “Aliviaderos y Obras de toma”. Este último artículo es una presentación detallada acerca del trampolín o salto en esquí empleado en funciones de disipación de energía.

Palabras-clave: cono de socavación; dientes deflectores; recta de los conos; trampolín; vuelo del chorro; vuelo del cono

ABSTRACT

The present article is the seventh of a series of seven, all relatives to the energy dissipators that can be used in hydraulic works. The whole group of these articles conform a monograph about the subject that is being prepared by the author, concluding it by the middle of the year 2017 and later on incorporating it to a new edition - in preparation - of the textbook "Spillways and Intake Structures". This last article is a detailed presentation about the hydraulic ski jump used with the function of energy dissipation.

Key words: undercut cone; chute blocks; straight line of the cones; hydraulic ski jump; flight of the jet; flight of the cone

INTRODUCCIÓN

El uso del trampolín, como elemento disipador de la energía del flujo que circula por un aliviadero, ha resultado bastante amplio; sin embargo, su empleo más frecuente en las obras se ha visto frenado en múltiples ocasiones por la carencia de información acerca de ellos (^{Pardo y Alegret 2012}).

En la literatura técnica existente hasta el año 2008, es posible encontrar numero sos ejemplos de trampolines, pero en general su adaptación a nuevas condiciones locales, resultaba muy difícil, si no imposible, sin un previo estu dio experimental de su comportamiento ante las nuevas condiciones de trabajo. La experiencia personal de los proyectistas o inves tigadores, resultaba en estos casos uno de los elementos más pode rosos a la hora de definir un esquema de trampolín en específico y sus posibles modificaciones ante determinadas situaciones. Precisamente en ese año 2008 el autor concluyó un proyecto de investigación científica gracias al cual se pudo disponer de un procedimiento confiable para valorar la estabilidad del trampolín atendiendo a la ocurrencia de una gran erosión que se produce justamente aguas abajo del mismo. A ese procedimiento se le denominará en lo sucesivo “Método de Pardo para evaluar la estabilidad del trampolín considerando la ocurrencia del cono de socavación”, el cual se presenta más adelante en este trabajo.

En el campo de las obras hidrotécnicas se denomina trampolín a la estructura que dispuesta al pie del cimacio, al final de la rápida o de una conducción forzada, posibilita el lanzamiento del chorro lo más lejos posible, de forma tal que no se compromete la estabilidad de la obra como consecuencia de la gran erosión que se produce aguas abajo. (^{Heller and Hager 2005}).

La disipación de gran parte de la energía del flujo se produce por impacto y turbulencia de la masa de agua al caer desde el trampolín (^{Pardo 2017}), (^{Peterka 1984}).

La erosión que se presenta aguas abajo de los trampolines adopta la forma de una hondonada conocida como “cono de socavación”. Sus dimensiones así como su ubicación respecto al trampolín u otra obra cercana, son los factores a tener en cuenta cuando se comparan distintas variantes de disipador de energía para una obra.

La profundidad y la distancia del punto más bajo del cono respecto al trampolín, así como el ancho del cono en la superficie del terreno, dependen de un conjunto de variables relativas a la geometría del trampolín, a la energía del agua respecto al nivel de la descarga en el río o canal de salida y a las características del terreno.

Hasta el presente se han utilizado trampolines de formas muy diversas: desde estructuras de sección rectangular con paredes laterales o sin ellas y fondo plano horizontal o con pendiente adversa, hasta trampolines de fondo curvilíneo en las direcciones longitudinal y transversal del flujo. En todos los casos lo que se ha pretendido es disminuir las dimensiones del cono y alejar lo más posible su ubicación respecto al trampolín.

A mediados de la década de los años 80 del pasado siglo fue defendida una tesis de doctorado en el Centro de Investigaciones Hidráulicas de Cuba mediante la cual se hizo un significativo aporte al conocimiento de los trampolines, que permitió proponer el procedimiento para el diseño hidráulico del trampolín CIH. (^{González 1986}).

Geometría del Trampolín

La geometría del trampolín es variable y depende en gran medida del punto de vista en que ésta se analice: en perfil o en planta.

En perfil el trampolín puede clasificarse como:

1. De pendiente horizontal

2. De pendiente adversa

3. De forma curva

En planta pueden clasificarse como:

1. Trampolín plano

2. Trampolín divergente.

Cuando el trampolín es divergente es necesario usar paredes o tabiques que obliguen al agua a correr por sobre todo el trampo lín.

Resulta ilógico el uso de trampolines convergentes, pues esto implicaría un aumento del gasto específico sobre el trampolín y con ello un aumento también de la socavación aguas abajo del mismo, aspecto este último que atenta contra el propósito funda mental que se persigue con el diseño de este objeto de obra; esto es, que la estabilidad del propio aliviadero y de otras obras cercanas no corran riesgos de inestabilidad por erosiones en sus cercanías derivadas de la ocurrencia del mencionado cono de socavación.

En la figura 1 se ilustra de forma esquemática cada una de las clasificaciones de los trampolines según su geometría.

Figura 1 Tipos de trampolines de uso más frecuente 

Accesorios que pueden ser usados en los trampolines

Es práctica frecuente en el diseño de estas estructuras emplear “dientes deflectores” para asegurar una mayor dispersión y aireación del chorro, obteniéndose en consecuencia una reducción de la erosión. La forma básica de los mismos es la de una cuña, pudiendo ser prismáticos o no y de una sola o doble pendiente o con un cierto grado de curvatura de su cara superior.

Está demostrado que la colocación de dientes deflectores disminuye en aproximadamente un 30 % la profundidad del cono con respecto al cono del mismo trampolín sin dientes.

Existen distintos tipos de dientes deflectores que pueden ser clasificados como:

• De una pendiente

• De dos pendientes

• De forma curva

• En forma de prisma.

En la figura 2 se ilustra esquemáticamente cada una de las clasificaciones antes mencionadas.

Figura 2 Tipos de dientes deflectores de uso más frecuente en trampolines 

Propósito que se persigue con el cálculo de un trampolín

Con el cálculo de un trampolín se persigue, como objetivo princi pal, buscar una solución capaz de lograr que la disipación de la energía se produzca lo más alejada posible de la estructura, para con ello obtener como resultado la formación de un cono de socavación donde el talud aguas arriba no afecte la losa de fondo de la rápida u otra obra cercana, pues de esto suceder se produciría el fallo de dicha estructura. En la figura 3 se ilustra un esquema de un trampolín y se ilustran los principales parámetros

Figura 3 Esquema típico de un trampolín con sus principales parámetros 

Ubicación del trampolín

En la ubicación del trampolín deben tenerse en cuenta los si guientes aspectos:

1.- Se deberá ubicar siempre por encima del nivel de agua del canal de evacuación para que la descarga del flujo se realice libremente, en la práctica se coloca -siempre que sea posible- el trampolín de dos a tres metros por encima de la superficie del agua en la descarga (P = 2 a 3 m). En caso contrario ocurrirá la formación de un salto hidráulico en el trampolín lo cual significaría el funcionamiento de dicha estructura en condiciones no previstas que podrían propiciar la destrucción del mismo. Si P es menor que 2 metros la descarga del agua desde el trampolín no es totalmente libre y si P es mayor de 3 metros, las dimensiones del cono crecen de manera significativa.

2.- La posición final del trampolín deberá garantizar una veloci dad en el chorro tal que permita que el mismo sea lanzado lo más lejos posible de la obra. Se debe tener presente además, que el chorro al caer sobre el agua lo haga con una inclinación ß = 30° - 35°.

3.- Hay que tener en cuenta los gastos pequeños y su efecto sobre el terreno.

Cimentación de los trampolines

Los trampolines suelen estar sustentados por pilotes o dentellones.

En el caso de los pilotes se toma con frecuencia, como factor de seguridad, que la punta de dichos elementos no deberá estar nunca por encima del punto más bajo del cono de socavación.

Tirante en el trampolín

En el trampolín se acepta que el tirante de circulación sea igual al tirante que llega a la entrada (final de la rápida).

Criterios para el diseño de un trampolín tipo CIH

Pasos a seguir:

1 - Cálculo de la velocidad y el número de Froude a la entrada del trampolín. Obsérvese que la formulación que se presenta responde a la forma empleada en Europa oriental para el número de Froude.

$V_1=\frac{Q}{b{h}_1}$ (1)

$F_{r1}=\frac{V_1^2}{g{h}_1}$ (2)

2 - Comprobar si F_r1 cumple la siguiente restricción. $7\le F_{r1}\le 39$ Si esta restricción se cumple se podrá seguir adelante con esta metodología.

• Si no se cumple habrá que recurrir a otra solución de trampolín y modelar la misma en el laboratorio.

3 - Cálculo del (F _r1-max ) para conocer si se producirá o no cavitación en los deflectores.

$F_{r1-\max }=\frac{\mathrm{4,32}\left(h_1+H_{atm}-H_v\right)}{h_1};\left(H_{atm}-H_v\right)\approx 10m$ (3)

• Si se cumple que F _r1 < F _r1-max entonces se podrán usar deflectores pues no existe peligro de que ocurra cavitación en la cara posterior de ellos.

4- Dimensionamiento del trampolín y los deflectores. Ver la figura 4.

a) Longitud del trampolín

$L_{mín}=4h_1$ (4)

Figura 4 Características generales del trampolín CIH 

b) Altura del deflector (Y ₁ )

$Y_1=\left(\mathrm{0,3}~\mathrm{0,4}\right)h_1$ (5)

c) Longitud del deflector (X ₁ )

$X_1=2Y_1$ (6)

d) Ancho del deflector (Z ₁ )

$Z_1=X_1$ (7)

e) Número de deflectores (n)

$n=\frac{\mathrm{0,5}b}{Z_1} \left(8\right)$

seleccionar el valor definitivo de n, se deberá escoger un número impar de deflectores, para con ello garantizar la colocación de uno de ellos en el eje del trampolín.

f.- Ubicación de los deflectores (a, c y d)

$a=\mathrm{0,25}{Z}_1$ (9)

$c=Z_1$ (10)

$d=\frac{b-\left(\mathrm{2,5}+n\right)Z_1}{n-3}$ (11)

g.- Altura de las paredes (h)

$h=h_1+BL$ (12)

donde: BL: bordo libre (BL = 0,6 h ₁ )

Cálculo de la geometría del chorro

Longitud de vuelo del chorro (L _v )

$L_v=\left[\frac{V_1^{2}sen\varphi \cos \varphi }{g}+V_1\cos \varphi \sqrt{\frac{V_1^{2}se{n}^2\varphi }{g^2}+\frac{2\left(P+h_1\right)}{g}}\right]K$ (13)

donde:

V 1	- velocidad de llegada
K	- factor que toma en cuenta la influencia del aire en el chorro de agua = 0,9 (Según recomendaciones del USBR)
g	- Aceleración de la gravedad

$\varphi =\frac{{\psi }^{"}+{\psi }_i^{"}}{2}$ (ángulo medio de salida del chorro) (14)

donde: Ψ" y Ψ _i " se obtienen de la tabla 1

Tabla 1 Coeficientes para el cálculo del ángulo medio de salida del chorro 

Y 1 / h 1	0,30	0,35	0,40	0,45	0,50	0,55	0,60
Ψ ^“	11,5^o	12,5^o	13,5^o	14,5^o	15,4^o	16,3^o	17,0^o
Ψ i ^”	7^o	9^o	10^o	10,8^o	11,7^o	12,5^o	13,3^o

Inclinación del chorro respecto a la superficie de la lámina aguas abajo (β)

$\beta =\arctan \left(\sqrt{{\tan }^2\varphi +\frac{2g\left(P+h_1\right)}{V_1^2{\cos }^2\varphi }}\right)$ (15)

Longitud de vuelo por el cono (L _vc )

$L_{vc}=L_v+\frac{t_0}{\tan \beta }$ (16)

Si ß < 30° no se puede hallar por el método existente.

Cálculo de la profundidad del cono de socavación (t _o )

En la literatura especializada se presenta una gran variedad de métodos para este fin; a continuación se exponen algunos de ellos. Se realizará en el caso de trampolín con deflectores por medio de las expresiones siguientes:

• Para suelos sueltos (gravas, arena, etc)

Según AMIROV:

$t_0=K_0{Z}_0^{\mathrm{0,25}}{h}_{cr}^{\mathrm{0,75}}$ (17)

donde:

$K_0=K_d{K}_b{K}_a{K}_e{K}_{def}$ (18)

K _d : Coeficiente que tiene en cuenta el material del lecho aguas abajo y se calcula como:

$K_d=\frac{\mathrm{4,10}}{{\left[1+\frac{d_{90}}{d_0}\right]}^{\mathrm{0,3}}}$ (19)

Tanto d ₀ como d ₉₀ se sustituyen en milímetros, Amirov recomienda usar d ₀ = 0,2 mm.

K _β : Coeficiente que tiene en cuenta el ángulo de inclinación del chorro aguas abajo.

$K_{\beta }=\mathrm{4,43}{\left(\frac{\beta }{{90}^0}\right)}^{\mathrm{0,20}} si \beta < 30° \left(20a\right)$

$K_{\beta }=\mathrm{4,29}{\left(\frac{Z_o}{h_{cr}}\right)}^{\mathrm{0,05}} si \beta > 30° \left(20b\right)$

$h_{cr}=\sqrt[3]{\frac{Q^2}{g{b}^2}}$ (21)

K _a : Coeficiente de aireación del chorro

$K_a=\mathrm{0,903}{\left(\frac{h_{cr}}{Z_o}\right)}^{\mathrm{0,15}} \left(22\right)$

$Z_0=P+h_1+\frac{V_1^2}{2g}$ (23)

$K_e{K}_{def}=\mathrm{0,70}:coeficientede estructuracondeflector$ (24)

Según STUDIENNICHNIKOV:

$t_o=K_d{K}_{\beta }{K}_a{K}_e{K}_{def}{Z}_o^{\mathrm{0,25}}{h}_{cr}^{\mathrm{0,75}}$ (25)

donde: K _d y K _β se calculan de forma similar al caso anterior

$K_a{K}_e{K}_{def}=\mathrm{0,70}$ (26)

Según MIRTSJULAVA:

$t_0=\left(\frac{3\eta U_{en}{b}_o}{W}-\mathrm{7,5}{b}_o\right)\frac{sen\beta }{1-\mathrm{0,175}\cot \beta }+\mathrm{0,25}t$ (27)

η = 1,5 (para laboratorio); = 2,0 (para la naturaleza) - coeficiente de turbulencia

$U_{en}=\sqrt{V_1^2+2g\left(P+h_1\right)}$ - velocidad de entrada en el bief inferior (28)

$b_o=\frac{\mathrm{0,8}q}{U_{en}}$ ancho del chorro al entrar al en la agua en la descarga (29)

$W=\sqrt{\frac{2g\left({\gamma }_p-{\gamma }_o\right)d_c}{\mathrm{1,75}{\gamma }_o}}$ - velocidad de arrastre de las partículas sueltas (30)

γ _p : peso específico del suelo.

γ _o : peso específico del agua aireada = 0,5 ton / m³

$d_c=d_{90}$

• Para cualquier tipo de suelo.

Según VIZGO:

$t_0=AK{q}^{\mathrm{0,5}}{Z}_o^{\mathrm{0,25}}$ (31)

donde:

$A=\mathrm{0,55}+\mathrm{0,3}\left(q/Z_0 \right) -\text{coeficiente de aireación} \left(32\right)$

coeficiente que toma en cuenta el tipo de suelo y β, según la tabla 2

Tabla 2 Coeficiente en función del tipo de suelo 

Suelo/β	0^0	12^0	25^0	40^0	60^0	90^0
muy débil	1,4	1,8	2,4	2,8	3,3	4,5
otros	1,4	1,7	2,0	2,4	2,7	3,3

Según LOPARDO (^{Lopardo y Sly 1992}):

$t_0=\mathrm{2,5}\varnothing Z_o{Z}_{*}^{\mathrm{0,5}}$ (33)

Φ = 1,3 - factor de seguridad

$Z_{*}=\frac{q}{\sqrt{g{Z}_0^3}}$ - número de caída (34)

• Para suelos cohesivos o arcillosos

Según MIRTSJULAVA:

$t_0=\left(\frac{\mathrm{8,3}{U}_{en}{b}_o}{V_{\Delta }}-\mathrm{7,5}{b}_o\right)\frac{sen\beta }{1-\mathrm{0,175}\cot \beta }+\mathrm{0,25}t$ (35)

donde:

$V_{\Delta }=\mathrm{1,25}\sqrt{\frac{2gm}{\mathrm{0,3}{\gamma }_o\eta }\left[\left({\gamma }_p-\gamma o\right)d+\mathrm{1,25}\left(C_f^{c}K+P_d+P_h\right)\right]}$ (36)

m: Cantidad de azolves y se acepta:

m = 1 cuando no hay azolves

m = 1,6 cuando hay azolves

d: diámetro promedio de agregados. Varía de 3 a 5 mm, generalmente se toma d = 3 mm

$C_f^c=\mathrm{0,035}C$ (37)

C: Cohesión del terreno

K = 0,5

$P_d=\frac{\mathrm{1,88}{\gamma }_o\alpha V_{\Delta }^{2}sen\beta }{g}$ - presión dinámica sobre los agregados (38)

$P_h=\propto {\gamma }_o{t}_o$ (39)

siendo α = 0,01

Como se puede observar de las expresiones anteriores, resulta imposible obtener una solución de forma directa pues el número de incógnitas es grande, lo cual implica la necesidad de entrar en un proceso iterativo para obtener sus respectivos valores. A continuación se recomienda una serie de pasos para la ejecución de dicha iteración así como un formato de tabla para ir recogien do los resultados que se obtienen en cada paso:

VΔ	to inicial	Pd	Ph	to final	| t0i - t0f |

procedimiento a seguir:

1) Iteración

1. Hacer P _h = P _d = 0

2. Determinar V _Δ

3. Cálculo de to inicial

4. Cálculo de P _d y P _h a través de sus respectivas expresiones

5. Cálculo de to final con los valores de P _d y P _h obtenidas en el paso anterior

Comprobar que $\left|t_{o-inicial}-t_{o-final}\right|\le 1m$ Si se cumple entonces $t_o=t_{o-final}$ i no se cumple se deberá proceder a la segunda iteración

2) Iteración

1. Hacer $t_o=t_{o-final}$ btenido en la iteración anterior

2. Cálculo de P _h y P _d

3. Cálculo de V _Δ

4. Cálculo de t _o-final con los valores obtenidos anteriormente

5. Comprobar que $\left|t_{o-inicial}-t_{o-final}\right|\le 1m$ i se cumple: entonces t _o = t _o-final

Si no se cumple, se continuarían las iteraciones hasta garantizar el requisito anterior (se deberán seguir los pasos correspondien tes a la 2^da iteración).

Debe tenerse presente que las expresiones de Vizgo y Mirtsjulava son para trampolines sin dientes, luego sus resultados deberán ser afectados por un factor de 0,70 para aquellos casos en los que sí estén presentes estos elementos.

MÉTODO DE PARDO PARA EVALUAR LA ESTABILIDAD DEL TRAMPOLÍN CONSIDERANDO LA OCURRENCIA DEL CONO DE SOCAVACIÓN

Investigaciones llevadas a cabo a comienzos del presente siglo por el autor en el Centro de Investigaciones Hidráulicas, han aportado criterios de diseño muy novedosos respecto al cono de socavación en particular y sobretodo con la seguridad del trampolín. Por su importancia se reproducen dichos resultados a continuación respetando la forma en que ya han sido publicados, lo que hace que se repitan algunos aspectos mencionados más arriba.

Ubicación del cono de socavación que se forma aguas abajo del trampolín

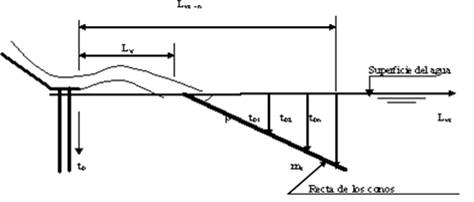
La ubicación del cono de socavación, entiéndase como posición del cono aquella en la que se produce la mayor profundidad t _o del mismo, viene dada por la ecuación (40) (^{Kiceliov 1961}):

$L_{vc}=L_v+\frac{t_0}{\tan \beta }$ (40)

donde:

L vc	- distancia horizontal desde el extremo final del trampolín hasta el lugar donde se produce la mayor profundidad del cono de socavación; comúnmente se le denomina “longitud de vuelo del cono”.
L v	- distancia horizontal desde el extremo final del trampolín hasta el lugar donde el chorro de agua entra a la superficie del agua en el canal de salida aguas abajo; comúnmente se le denomina “longitud de vuelo del chorro”.
t o	- profundidad del cono de socavación.
β	- ángulo de entrada del chorro a la superficie del agua en el canal de salida.

L _v se determina según (^{Kiceliov 1961}):

$L_v=\left[\frac{V_1^{2}sen\varphi \cos \varphi }{g}+V_1\cos \varphi \sqrt{\frac{V_1^{2}se{n}^2\varphi }{g^2}+\frac{2\left(P+h_1\right)}{g}}\right]K$ (41)

β se determina según (^{Kiceliov 1961}):

$\beta =\arctan \left(\sqrt{{\tan }^2\varphi +\frac{2g\left(P+h_1\right)}{V_1^2{\cos }^2\varphi }}\right)$ (42)

Obsérvese que las variables del lado derecho de las ecuaciones (41) y (42) son fijas para una condición de diseño determinada y por tanto L _v también lo es. A partir de lo anterior se puede concluir que la expresión (40) corresponde a una línea recta de pendiente:

$m_c=\frac{1}{tan\beta } \left(43\right)$

que intercepta al eje L _vc en L _v . Se entiende que el sistema de ejes L _vc - t _o tiene su origen de coordenadas en la superficie del agua aguas abajo y exactamente debajo de la salida del trampolín, con el eje L _vc en dirección horizontal y sentido positivo hacia aguas abajo, mientras el eje t _o se desarrolla verticalmente y sentido positivo hacia abajo.

La variable t _o según se ha descrito, tiene varias formas de cálculo y a cada una corresponde un valor de L _vc , todos esos pares de valores (L _vc ; t _o ) quedan situados sobre una recta tal y como lo expresa la expresión (40) a la que en lo sucesivo se le denominará “recta de los conos”, la cual como se verá más adelante desempeña un papel esencial en el diseño confiable de un trampolín. Ver figura 5.

Figura 5 Representación de la recta de los conos 

Al realizar los cálculos correspondientes de β y L _v para 40 combinaciones diferentes de la altura P, el tirante h ₁ y la velocidad V ₁ en el trampolín, todos ellos seleccionados atendiendo a valores de factible ocurrencia práctica; se pudo constatar que la pendiente de la recta de los conos oscila entre valores extremos m _c = 0,79 a 2,69.

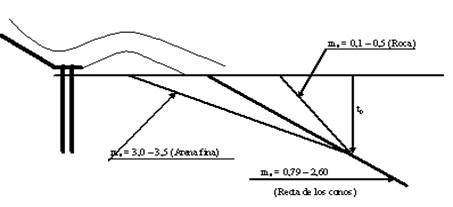
Por otro lado, en la tabla 3 presentada por Kiceliov en 1972 se muestran los valores del talud de reposo m _s en función del tipo de suelo. Este talud de reposo del suelo juega un papel importante en el diseño del trampolín y el correspondiente pronóstico del cono de socavación por cuanto las paredes del cono tienden a tomar un talud cercano al de reposo, teóricamente hablando, igual al de reposo. (^{Kiceliov 1961})

La interpretación combinada de lo antes expresado y la tabla 3, permite establecer las conclusiones siguientes:

1. Independientemente de los parámetros hidráulicos de diseño del trampolín (P, h ₁ y V ₁ ), aquellos construidos sobre arena fina tendrán un cono de socavación que sale a la superficie en un punto situado a la izquierda de la recta de los conos debido a que m _s > m _c y por tanto pudiera estar en peligro la estabilidad del aliviadero; sin embargo, los trampolines construidos sobre roca tendrán un cono que teóricamente saldría siempre a la derecha de la recta de los conos, lo que significa que nunca estará en peligro la estabilidad del trampolín como consecuencia del cono de socavación. Obviamente en la práctica lo que ocurrirá en este caso es que el cono saldrá a la superficie coincidiendo con el punto donde el chorro incide sobre la superficie del agua. Ver figura 6.

Figura 6 Relación grafica entre m_s y m_c 

2. Para el resto de los tipos de suelos se deberá realizar un análisis para cada caso, verificándose que:

• Si m _c ≥ m _s ⇒ el talud de aguas arriba del cono de socavación sale a la derecha o sobre la recta de los conos y el aliviadero no corre riesgos.

• Si m _c < m _s ⇒ el talud de aguas arriba del cono de socavación sale a la izquierda de la recta de los conos y el aliviadero pudiera correr riesgos.

3. A tenor con las dos conclusiones anteriores resulta evidente que durante el proceso de diseño, el proyectista deberá tener en cuenta la incidencia de P, h ₁ y V ₁ en las consecuencias del cono de socavación respecto al propio aliviadero y por tanto, adecuadas modificaciones en las dimensiones hidráulicas del aliviadero pueden conllevar resultados muy favorables en relación con la estabilidad del mismo. Esto por supuesto teniendo en cuenta el tipo de suelo en que será emplazado.

Dicho en otras palabras, modificando la posición del trampolín respecto a la superficie del agua en el canal de salida P y/o el ancho de la rápida (significa variar tirante h ₁ y velocidad del flujo V ₁ , ambos al final de la rápida), se logrará variar β y con ello L _v , t ₀ y L _vc hasta lograr que la pendiente de la recta de los conos m _c se modifique y sea mayor que m _s y por tanto el aliviadero no corra riesgo producto del cono de socavación.

Un análisis similar se puede realizar respecto a cualquier otra estructura que se encuentre próxima a la zona del disipador de energía.

Por otro lado, se considera que el cono de socavación afecta la estabilidad del propio aliviadero cuando penetra debajo de la rápida, es decir, puede penetrar hasta debajo del propio trampolín y ello no afecta a la estructura del aliviadero.

De manera que si se sabe que el cono se produce aguas abajo del trampolín a una distancia L _vc y se define la longitud del propio trampolín como L _tram , es fácil, sabiendo que la salida del cono desde su punto más bajo hasta el nivel trampolín, es X _cono = m _s (t _o + P), entonces si:

$L_{tram}+L_{vc}>m_s\left(t_o+P\right)$ (44)

Ello implica que el cono no afecta al aliviadero; en caso contrario sí lo afecta.

Si de todas formas se desea estimar la profundidad del cono de socavación, se sugiere el empleo del método de Lopardo, dado su origen desde observaciones de campo.

Tabla 3 Talud de reposo “m _s ” para diferentes tipos de suelos [^{Kiceliov 1961}]  

Suelo	m s
Arena fina	3,0 - 3,5
Arena	2,5 - 3,0
Rocoso Tierra Arena gruesa	2,0 - 2,5
Tierra arcillosa ligera Tierra arenosa densa	1,5 - 2,0
Grava y arena - grava Cascajo grueso	1,5
Arcilla pesada Loess denso Arcilla	1,0 - 1,5
Arcilla densa pesada Aluvión compacto	1,0
Roca	0,1 - 0,5

CONCLUSIONES

• El trampolín o salto en esquí es un excelente disipador de energía cuando las condiciones en la descarga y aguas abajo no se ven afectadas por erosiones locales intensas producto de la formación del cono de socavación inherente a este tipo de disipador.

• El uso de la recta de los conos y las conclusiones que aquí se presentan constituyen una importante solución relacionada con las dudas que se tenían acerca de la seguridad del propio trampolín y de obras cercanas, ante eventuales erosiones bajo las mismas.

RECONOCIMIENTO

El autor desea dejar constancia de su agradecimiento al actual ingeniero Dayron Martí Díaz, quien como estudiante de ingeniería hidráulica culminó sus estudios mediante la tesis de grado “Disipadores de energía” tutelado por el autor del presente trabajo, la cual fue de inestimable ayuda para el logro de la mencionada monografía.

REFERENCIAS

González J. E. (1985). “Diseño hidráulico de disipadores de energía tipo trampolín”. Tesis de Doctorado. Ciudad de La Habana. 1985.

Heller V. and Hager W. (2005) - “Ski Jump Hydraulics”. Journal of Hydraulic Engineering, Vol 131, No. 5, pp. 347-355, ISSN 0733-9429, ASCE, USA.

Kiceliov P. C. (1961) “Manual de Cálculos Hidráulicos” (en ruso), Editorial Energía, Moscú.

Lopardo R. y Sly E. (1992). “Constatación de la profundidad máxima de erosión aguas abajo de aliviaderos en salto de esquí”. Revista Latinoamericana de Hidráulica. No. 4. pp. 7-23, ISSN 1011-7563. Comité Regional Latinoamericano de la Asociación Internacional de Investigaciones Hidráulicas (IAHR), Sao Paulo, Brasil.

Pardo R. y Alegret E. (2012). “Diseño hidráulico de aliviaderos y obras de toma para presas”. Editorial Félix Varela, ISBN 978-959-07-1692-8, La Habana.

Pardo R. (2017). “Monografía sobre disipadores de energía”. ISBN: 978-959-261-565-6. Departamento de Ediciones CUJAE, La Habana, Cuba.

Peterka A. J. (1984). “Hydraulic design of stilling basins and energy dissipators”. Engineering monograph No. 25. United States Bureau of Reclamation (USBR). Denver, Colorado, USA.

Recibido: 09 de Mayo de 2018; Aprobado: 07 de Marzo de 2019

Rafael Pardo Gómez. Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). email: [e-mail]