Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Informática Médica
versión On-line ISSN 1684-1859
RCIM vol.5 no.1 Ciudad de la Habana ene.-jun. 2013
ARTÍCULO ORIGINAL
Segmentación de imágenes cerebrales de Resonancia Magnética basada en Redes Neuronales de Regresión Generalizada
Segmentation of Magnetic Resonance images of the brain based on Generalized Regression Neural Networks
Yamileidy Monne Clemente,I Diana Monne Roque,II
IUniversidad de Oriente, Cuba. E-mail: ymonne@csd.uo.edu.cu
IIUniversidad de Ciencias Informáticas, La Habana, Cuba. E-mail: dmonne@uci.cu
El análisis de los cambios estructurales del cerebro a través de imágenes de Resonancia Magnética puede proveer información útil para el diagnóstico y el manejo clínico de los pacientes con demencia. Si bien el grado de sofisticación alcanzado por el equipamiento de Resonancia Magnética es alto, la cuantificación de estructuras y tejidos aún no ha sido completamente solucionada. Las segmentaciones que estos equipos permiten en la actualidad fracasan en aquellas estructuras donde los bordes no están claramente definidos. En este trabajo se presenta un método de segmentación automática de imágenes de Resonancia Magnética cerebrales basada en la utilización de Redes Neuronales de Regresión Generalizada utilizando algoritmos genéticos para el ajuste de los parámetros. La red se entrena a partir de una sola imagen y clasifica al resto de ellas siempre que las imágenes de Resonancia Magnética hayan sido adquiridas con el mismo protocolo. Un método de medición de la atrofia progresiva y sus posibles cambios frente a un efecto terapéutico debe ser fundamentalmente automático y por lo tanto independiente del radiólogo.
Palabras clave: imágenes, resonancia magnética, segmentación, redes neuronales, algoritmos genéticos.
ABSTRACT
The analysis of structural changes in the brain through Magnetic Resonance Images may provide useful information for the diagnosis and clinical management of patients with dementia. While the degree of sophistication achieved by the MRI equipment is high, the quantification of structures and tissues has not been completely solved. The segmentations that these equipment provide nowadays, fail on those structures where the edges are not clearly defined. This paper presents a method for automatic segmentation of magnetic resonance images of the brain, based on the use of generalized regression neural networks using genetic algorithms for adjusting parameters. The network is trained from a single image and classifies rest of them whenever magnetic resonance images were acquired with the same protocol. A method of measuring the progressive atrophy and possible changes compared to a therapeutic effect should be essentially automatic and therefore independent of the radiologist.
Key words: images, magnetic resonance, segmentation, neural networks, genetic algorithm.
INTRODUCCIÓN
El estudio a través de imágenes de los cambios estructurales del cerebro puede proveer información útil para el diagnóstico y el manejo clínico de los pacientes con demencia. Las imágenes de Resonancia Magnética (R.M.) pueden mostrar anormalidades que no son visibles en la Tomografía Computada. Asimismo tienen el potencial de detectar señales de anormalidad, permitiendo un diagnóstico diferencial entre la enfermedad de Alzheimer y la demencia vascular. Mientras que en las demencias vasculares la observación directa de las imágenes de R.M. permite un inmediato diagnóstico, el análisis estructural de este mismo tipo de imágenes en la enfermedad de Alzheimer tiene un rol muy importante y más complejo porque permite evaluar cambios tales como la atrofia cortical.1 Mientras esta manifestación celular de la enfermedad no puede ser estudiada in vivo, la atrofia que produce puede ser observada en las imágenes de R.M. cerebral y cuantificada a partir del Procesamiento Digital de Imágenes.2
El único método que se utiliza en nuestro país en la clínica de rutina para la medición de la atrofia es la evaluación visual del radiólogo y su opinión sobre si los surcos o el volumen ventricular están fuera del rango de normalidad.3 Numerosas técnicas han sido desarrolladas y aplicadas con el fin de obtener una segmentación a partir de las imágenes multiespectrales de R.M.4,5 El uso de técnicas de patrones para segmentar conjuntos de datos en imágenes de R.M. ha sido desarrollado ampliamente y descrito en la literatura.5,6 Sin duda cada aproximación tiene sus ventajas y desventajas. La mayoría son computacionalmente costosas pero sobre todo lo más difícil es encontrar simultáneamente automatización y exactitud en los resultados. Aquellas técnicas que segmentan con mayor exactitud son semiautomáticas, es decir son operador dependientes.7-10
En este trabajo se presenta un método de segmentación de imágenes de R.M. cerebrales basada en la utilización de Redes Neuronales de Regresión Generalizada (GRNN) utilizando algoritmos genéticos para el ajuste de los parámetros. Esta propuesta permite detectar y cuantificar los diferentes tejidos cerebrales de una manera automática, más sensible y esencialmente menos subjetiva y dar así un primer paso hacia el diagnóstico temprano de la atrofia cerebral. Este trabajo está organizado de la siguiente manera: en la sección siguiente se presentan algunas definiciones convencionales de Redes Neuronales de Regresión Generalizada, Algoritmos Genéticos y se describe el método propuesto. En la sección 3, se presentan algunos resultados experimentales prometedores y finalmente en la sección 4 se presentan las conclusiones del trabajo.
MATERIALES Y MÉTODOS
Redes neuronales de regresión generalizada
Las Redes de Regresión Generalizada (GRNN, Generalized Regression Neural Networks) son un tipo de Redes de Funciones de Base Radial (RBF) normalizadas, donde existe una celda de la capa escondida correspondiente a cada patrón de entrenamiento. El algoritmo de redes neuronales a aplicar para el procesamiento de señales biomédicas y/o biológicas se basa en el clasificador Bayes-Parzen11 y su arquitectura en la de las redes probabilísticas o de funciones de Base Radial.12 Este tipo de redes está basado en la Teoría de Regresión No lineal. Realiza una buena aproximación o mapeo de funciones entrada-salida a partir de los datos de entrenamiento. A medida que el conjunto de entrenamiento crece, el error se aproxima a cero. Se considera como variable independiente al conjunto de vectores o patrones de entrada X, y a la variable dependiente y como un escalar. Es ampliamente aceptado que el mejor valor predicho para y (en el sentido de mínimo error cuadrático esperado) es su esperanza condicional dado x. Así el error a minimizar está dado por la siguiente expresión:

En la práctica nunca es conocida la densidad conjunta ![]() . Pero es posible utilizar el estimador de Parzen multivariado para aproximar esa función densidad conjunta. Specht demostró que el valor de la salida puede ser estimado a partir de:
. Pero es posible utilizar el estimador de Parzen multivariado para aproximar esa función densidad conjunta. Specht demostró que el valor de la salida puede ser estimado a partir de:

Donde ![]() es la salida deseada j cuando i es el vector de entrada y
es la salida deseada j cuando i es el vector de entrada y ![]() es la estimación de la función densidad conjunta dada por:
es la estimación de la función densidad conjunta dada por:
![]()
La expresión de ![]() es similar a la de z de las RBF, donde en lugar de pesar los valores del estimador de la función densidad por los pesos adaptables
es similar a la de z de las RBF, donde en lugar de pesar los valores del estimador de la función densidad por los pesos adaptables ![]() se las multiplica por el valor deseado de la salida
se las multiplica por el valor deseado de la salida ![]() dada la entrada i. Así las salidas son un promedio pesado de los valores objetivos o deseados de los casos de entrenamiento cercanos al patrón de entrada. Los únicos parámetros libres que deben adaptarse son las dispersiones o anchos de las unidades RBF (
dada la entrada i. Así las salidas son un promedio pesado de los valores objetivos o deseados de los casos de entrenamiento cercanos al patrón de entrada. Los únicos parámetros libres que deben adaptarse son las dispersiones o anchos de las unidades RBF (![]() ). En consecuencia no es necesario "adaptar" los pesos de las conexiones a través de un entrenamiento repetitivo, lo que se traduce en una mayor velocidad de aprendizaje, dado que el único proceso es la ubicación de los centros de las funciones densidad y el ajuste de los
). En consecuencia no es necesario "adaptar" los pesos de las conexiones a través de un entrenamiento repetitivo, lo que se traduce en una mayor velocidad de aprendizaje, dado que el único proceso es la ubicación de los centros de las funciones densidad y el ajuste de los ![]() . Es factible utilizar métodos de computación evolutiva para la búsqueda del mejor valor para los mismos, con el objetivo de obtener el mínimo error. Es posible considerar a las GRNN como un aproximador universal para funciones suaves. Así, debería ser factible resolver cualquier problema de aproximación de funciones disponiendo de datos suficientes. El inconveniente principal de estas redes, como el de los métodos de kernels en general, es que sufren la "maldición de la dimensionalidad"; por lo tanto la cantidad de patrones de entrenamiento es una variable limitante para la aplicación de este tipo de predictores.
. Es factible utilizar métodos de computación evolutiva para la búsqueda del mejor valor para los mismos, con el objetivo de obtener el mínimo error. Es posible considerar a las GRNN como un aproximador universal para funciones suaves. Así, debería ser factible resolver cualquier problema de aproximación de funciones disponiendo de datos suficientes. El inconveniente principal de estas redes, como el de los métodos de kernels en general, es que sufren la "maldición de la dimensionalidad"; por lo tanto la cantidad de patrones de entrenamiento es una variable limitante para la aplicación de este tipo de predictores.
Algoritmos genéticos
Los Algoritmos Genéticos (A.G.) son elementos de la Computación Evolutiva y dentro de ella son los métodos utilizados para resolver problemas de optimización basados en la selección natural, proceso que deviene de la evolución biológica.13-16 Los Algoritmos Genéticos son métodos de optimización que permiten hallar (![]() ) tales que F(
) tales que F(![]() ) sea máximo (o mínimo). En un algoritmo genético, tras parametrizar el problema en una serie de variables, (
) sea máximo (o mínimo). En un algoritmo genético, tras parametrizar el problema en una serie de variables, (![]() ) se codifican en un cromosoma (secuencia de bits). Todos los operadores que se utilizan en un algoritmo genético se aplican sobre estos cromosomas o sobre poblaciones de ellos. Un algoritmo genético es independiente del problema, cualidad que aporta a su robustez por ser útil para cualquier problema, pero a la vez a su debilidad dado que no está especializado en ninguno. Las soluciones codificadas en un cromosoma compiten para ver cuál constituye la mejor, aunque no necesariamente la mejor de todas las soluciones posibles. El ambiente, constituido por otros individuos o soluciones, ejercerá una presión selectiva sobre la población, de forma que sólo los mejor adaptados (aquellos que resuelvan mejor el problema) sobrevivan o leguen su material genético a las siguientes generaciones, proceso similar a la evolución de las especies. La diversidad genética se introduce mediante operaciones que implementan mutaciones y reproducción. El proceso de codificación es el paso inicial del algoritmo genético. Cada cromosoma tiene varios genes, que se corresponden con los parámetros del problema. Para poder realizar las operaciones con estos genes es necesario codificarlos en una cadena, es decir, una serie de símbolos (números o letras) que generalmente va a estar compuesta de ceros y unos. Los algoritmos genéticos modifican en forma repetida a los integrantes de una población de soluciones individuales representada por cromosomas. En cada paso el algoritmo selecciona individuos provenientes de la población actual como padres y los utiliza para reproducir hijos para la próxima generación. En sucesivas generaciones la población evoluciona hacia la solución óptima. El campo de aplicación incluye una gran variedad de problemas de optimización no adecuados para los algoritmos de optimización estándar, incluyendo problemas donde la función objetivo es discontinua, no diferenciable, estocástica o no lineal. El algoritmo genético utiliza tres tipos esenciales de reglas en cada paso para crear una nueva generación a partir de la población actual:
) se codifican en un cromosoma (secuencia de bits). Todos los operadores que se utilizan en un algoritmo genético se aplican sobre estos cromosomas o sobre poblaciones de ellos. Un algoritmo genético es independiente del problema, cualidad que aporta a su robustez por ser útil para cualquier problema, pero a la vez a su debilidad dado que no está especializado en ninguno. Las soluciones codificadas en un cromosoma compiten para ver cuál constituye la mejor, aunque no necesariamente la mejor de todas las soluciones posibles. El ambiente, constituido por otros individuos o soluciones, ejercerá una presión selectiva sobre la población, de forma que sólo los mejor adaptados (aquellos que resuelvan mejor el problema) sobrevivan o leguen su material genético a las siguientes generaciones, proceso similar a la evolución de las especies. La diversidad genética se introduce mediante operaciones que implementan mutaciones y reproducción. El proceso de codificación es el paso inicial del algoritmo genético. Cada cromosoma tiene varios genes, que se corresponden con los parámetros del problema. Para poder realizar las operaciones con estos genes es necesario codificarlos en una cadena, es decir, una serie de símbolos (números o letras) que generalmente va a estar compuesta de ceros y unos. Los algoritmos genéticos modifican en forma repetida a los integrantes de una población de soluciones individuales representada por cromosomas. En cada paso el algoritmo selecciona individuos provenientes de la población actual como padres y los utiliza para reproducir hijos para la próxima generación. En sucesivas generaciones la población evoluciona hacia la solución óptima. El campo de aplicación incluye una gran variedad de problemas de optimización no adecuados para los algoritmos de optimización estándar, incluyendo problemas donde la función objetivo es discontinua, no diferenciable, estocástica o no lineal. El algoritmo genético utiliza tres tipos esenciales de reglas en cada paso para crear una nueva generación a partir de la población actual:
- Reglas de selección de los individuos, llamados padres, que contribuyen a la población de la nueva generación.
- Reglas de cruzamiento ("crossover") que combina dos padres para formar hijos de la nueva generación.
- Reglas de mutación que realizan cambios aleatorios en los individuos padres para generar los hijos.
Los pasos siguientes resumen el proceso general:
1. Creación de una población inicial aleatoria, codificada como secuencia de caracteres binarios.
2. Generación de secuencias de nuevas poblaciones o generaciones. Se utilizan los individuos de la generación actual para crear los de la próxima generación, siguiendo:
2a. Asignación de una puntuación a cada miembro de la población actual (con la función de evaluación diseñada ad hoc).
2b. Se realiza una escala de los puntajes de capacidad de los individuos de la generación actual. Se eligen padres de la nueva población a partir del ranking de capacidades.
2c. Se generan hijos a partir del conjunto de padres. Los hijos se producen por cambios aleatorios en un mismo padre (mutación) o por combinación de los vectores de un par de padres (cruzamiento).
El cruzamiento o crossover consiste en el intercambio de material genético entre dos cromosomas (Fig. 1a). El crossover es el principal operador genético. En la evolución natural, una mutación es un suceso bastante poco común (sucede aproximadamente una de cada mil replicaciones). En la mayoría de los casos las mutaciones son letales pero en promedio contribuyen a la diversidad genética de la especie. En un algoritmo genético esta operación tiene también un nivel de ocurrencia muy bajo. Una vez establecida la frecuencia de mutación, al generar el nuevo individuo se examina cada bit generado, y si su estado está por debajo del nivel de probabilidad se produce la mutación (Fig. 1b). De lo contrario se mantiene como está.
3. Se reemplaza la población actual por los hijos que forman la nueva generación. El algoritmo se detiene cuando se cumple uno de los criterios de detención: la cantidad de generaciones, un límite de tiempo de cálculo o un valor mínimo determinado para la función de evaluación, entre otros.
Método propuesto
El método propuesto presenta los siguientes pasos:
Etapa de Entrenamiento
- Paso 1: El operador selecciona entre 3 y 5 puntos de cada sustancia a segmentar, es decir líquido cefaloraquídeo (LCR), sustancia gris y sustancia blanca, de sólo una imagen de muestra, representativa del tipo de imágenes que se desearán segmentar.
- Paso 2: La GRNN es construida (y al mismo tiempo entrenada, característica propia de este tipo de redes) a partir de los valores de gris de los píxeles seleccionados en las diferentes imágenes (datos de entrenamiento, entrada), indicándosele los valores deseados en la salida, diferentes para cada sustancia. El valor óptimo del parámetro spread que se utiliza para entrenar la red (que corresponde a la dispersión de las gaussianas presentes a la red en su capa de entrada) se calcula mediante Algoritmos Genéticos. Se le indicó al A.G. un tamaño de población de 50 individuos. Se generó una población inicial aleatoria que se modificó en las sucesivas iteraciones en base a la función de evaluación. En esta aplicación dicha función se determinó a través del error calculado comparando la imagen clasificada obtenida como salida de la red y la imagen resultado previamente clasificada tomada como referencia. Se determina la cantidad de píxeles clasificados erróneamente, siendo éste el valor que se intenta minimizar. Se eligió una fracción de cruzamiento de 0.7 y una cantidad de 300 poblaciones como máximo. Se aceptaron los valores ofrecidos por defecto para los demás parámetros del A.G.
En estos dos pasos queda el sistema preparado para segmentar nuevas imágenes.
Etapa de Consulta
- Paso 3: Se consulta a la GRNN ya entrenada indicando como patrones de entrada a los niveles de gris de un nuevo conjunto de imágenes (T1, T2, PD). Se obtendrá así la clasificación para cada píxel de este nuevo caso.
- Paso 4: Se crea una nueva imagen con intensidades diferentes para cada píxel según la clase de sustancia a la que ha sido asignado.
- Paso 5: Se visualizan las estructuras segmentadas con diferentes colores. Se utilizaron imágenes de prueba pesadas en T1, en T2 y de densidad de protones (PD) corte coronal. Para el entrenamiento de las GRNN y para el cálculo de los errores se utilizaron imágenes ya clasificadas a través del software denominado BRAINS®.
Los algoritmos se programaron en Matlab 6.5 Se trabajó con funciones estándar de este lenguaje y con la librería específica Genetic Algorithm and Direct Search.
RESULTADOS
Se realizaron pruebas con más de 100 imágenes, variando la imagen a partir de la cual se entrenaba a la red tanto como los puntos iniciales que elige el operador en el proceso. En todos los casos el spread (![]() ) óptimo obtenido mediante el Algoritmo Genético se mantuvo en valores comprendidos entre 3.3262 y 4.1067 aun en repetidas ejecuciones para la misma imagen.
) óptimo obtenido mediante el Algoritmo Genético se mantuvo en valores comprendidos entre 3.3262 y 4.1067 aun en repetidas ejecuciones para la misma imagen.
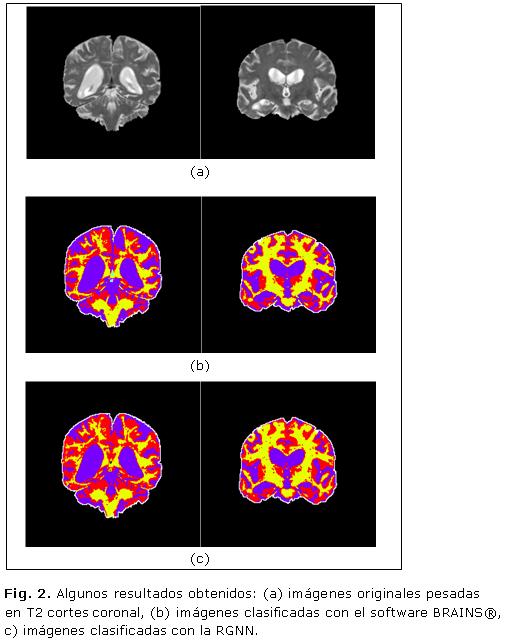
Se arriba a la conclusión de que es válido entrenar a la GRNN a partir de una sola imagen con un valor de spread comprendido en el rango hallado y clasificar luego al resto de ellas con un error inferior al 1 %, siempre que las imágenes de R.M. hayan sido adquiridas con el mismo protocolo. En la figura 2 se muestran imágenes de cerebro en corte coronal pesadas en T2, imágenes segmentadas a partir del método propuesto y las segmentadas por BRAINS® que fueron tomadas de referencia para validar el método propuesto.
CONCLUSIONES
Este trabajo presenta un método de segmentación automática de imágenes de R.M. cerebrales. El método es preciso y eficiente, siendo los resultados obtenidos prácticamente independientes del experto. La GRNN involucrada en el proceso se construye y entrena a partir de una única imagen, permitiendo clasificar otras imágenes tomadas con el mismo protocolo con un error menor que el 1 % y con un bajísimo tiempo de cálculo, característica propia de la etapa de consulta del tipo de redes neuronales utilizadas. Del éxito de la segmentación dependen la posterior cuantificación de la materia gris, blanca y LCR y por lo tanto la medición de la evolución de la atrofia cerebral.
REFERENCIAS BIBLIOGRÁFICAS
1. Davis P, Gray A, Albert M et al. The Consortium to Establish a Registry for Alzheimer's Disease. Neurology. 1992; 42:1676-1680.
2. Fox N, Freeborough P. Brain Atrophy Progression Measured from Registered Serial MRI: Validation and Application to Alzheimer Disease. J. Mag. Res. Imag. 1997; 7:1069-1075.
3. Manes F. Resonancia magnética nuclear en la Enfermedad de Alzheimer. Rev. Neurol. Arg. 2000;25: 29-37.
4. Raya SP. Low level segmentation of 3D resonance brain images. IEEE Trans. Med. Imaging; 1990; 9: 2.
5. Chen S, Wei-chun L, Chen C. Medical image understanding system based on Dempster-Shafer reasoning. SPIE Biomedical Imag. Processing II. San Jose, California; 1991.
6. Clarke LP et al. Comparison of Supervised Pattern Recognition Techniques and Unsupervised Methods for MRI Segmentation. Proc. SPIE Medical Imaging VI Conference, Vol. 1652, SPIE Press, Bellingham, WA: 668-677; 1992.
7. Gerig G, Martin J, Kikinis R. Unsupervised tissue type segmentation of 3D dual-echo MR head data. Image Vision Computer. 1992; 10: 349-360.
8. Alfano B, Brunetti B et al. Unsupervised, automated segmentation of the normal brain using multispectral relaxometric magnetic resonance approach. Magn. Reson. Med. 1992; 37: 84-93.
9. Bartlett T, Vannier M, Mc Keel D, Gado M, Hildebolt C, Walkup R. Interactive segmentation of cerebral gray matter, white matter, and CSF: photographic and MR images. Comp. Med. Imag. Graphics. 1994 18(6): 449-460.
10. Abras G, Ballarin V, González M. Aplicación de Reconocimiento de Patrones en la Clasificación de Tejido Cerebral. Actas del Congreso Argentino de Bioingeniería. Tafí del Valle. Septiembre 2001. (Publicadas en CD).
11. Parzen E. On estimation of a probability density function and mode. Annals of Mathematical Statistics. 1962; 33: 1065-1076.
12. Specht D. A General Regression Neural Network. IEEE Transactions on Neural Networks. 1991;2 (6): 588-596.
13. Holland JH. Outline for a logical theory of adaptive systems. J. Assoc. Comput, Mach. 1962; 3: 297-314.
14. Holland JH. Adaptation in Natural and Artificial Systems. Ann Arbor, MI: Univ. of Michigan Press; 1975.
15. De Jong KA. On using genetic algorithms to search program spaces. Proc. 2nd Int. Conf. on Genetic Algorithms and Their Applications. Hillsdale, NJ: Lawrence Erlabaum: 210-216; 1987.
16. Goldberg DE. Genetic Algorithms in Search, Optimization & Machine Learning. Addison-Wesley; 1989.
Recibido: 11 de mayo de 2013.
Aprobado: 16 de junio de 2013.